【新課程】東京書籍：Advanced数学Ⅰ[701]

p.169 問1　中央値 \(12\)
　第１四分位数 \(9\)
　第３四分位数 \(14\)

→ 平均値・中央値・最頻値
→ 箱ひげ図

p.169 問2① 正しい
② 正しくない

p.170 問3$$~~~0~,~2~,~-1~,~1~,~-2$$

p.171 問4分散 \(2\)、標準偏差 \(1.41\)
→ 分散と標準偏差

p.172 問5標準偏差が \(1\) 点であるＢさんの方が安定している

p.173 問6\(x~,~y\) の平均値を \(\overline {x}~,~\overline {y}\) とすると、$$~~~\overline {y}=a\overline {x}+b$$\(x~,~y\) の分散を \(s_x^2~,~s_y^2\) とすると、$$~~~s_y^2=a^2s_x^2$$\(x~,~y\) の標準偏差を \(s_x~,~s_y\) とすると、$$~~~s_y=|a| s_x$$

p.174 問7変数 \(y\) は、変数 \(x\) の \(n\) 個の値より、$$\begin{eqnarray}~~~y_1&=&ax_1+b\\[2pt]~~~y_2&=&ax_2+b\\[2pt]~~~&\vdots&\\[2pt]~~~y_n&=&ax_n+b\end{eqnarray}$$変数 \(y\) の平均値 \(\overline {y}\) より、$$~~~n\overline {y}=y_1+y_2+\cdots+y_n$$上の式を代入すると、$$\begin{eqnarray}~~~n\overline {y}&=&(ax_1+b)+\cdots+(ax_n+b)\\[2pt]~~~n\overline {y}&=&(x_1+x_2+\cdots+x_n)+nb\end{eqnarray}$$両辺を \(n\) で割ると、$$~~~\overline {y}=a\frac{\,x_1+x_2+\cdots+x_n\,}{\,n\,}+b$$ここで、$$~~~\overline {x}=\frac{\,x_1+x_2+\cdots+x_n\,}{\,n\,}$$より、$$~~~\overline {y}=a\overline {x}+b$$

p.174 問8　平均値 \(50\)
　分散 \(13.0~(12.96)\)
　標準偏差 \(3.6\)

p.175 参考 問1　分散 \(0.8\)

p.180 問1５人の身長をメリメートルにすると、$$~~~1800~,~1720~,~1650~,~1720~,~1660$$平均値 \(\overline {x}\) は、$$~~~\overline {x}=1710$$\(x-\overline {x}\) は、$$~~~90~,~10~,~-60~,~10~,~-50$$\((x-\overline {x})^2\) は、$$~~~8100~,~100~,~3600~,~100~,~2500$$合計 \(14400\) となる
\((x-\overline {x})(y-\overline {y})\) は、$$~~~450~,~90~,~300~,~20~,~550$$合計 \(1410\) となる
これより、相関係数 \(r\) は、$$\begin{eqnarray}~~~r&=&\frac{\,\frac{\,1\,}{\,5\,}\cdot1410\,}{\,\sqrt{\frac{\,1\,}{\,5\,}\cdot14400}\cdot\sqrt{\frac{\,1\,}{\,5\,}\cdot256}\,}\\[3pt]~~~&=&\frac{\,1410\,}{\,\sqrt{14400}\cdot\sqrt{256}\,}\\[3pt]~~~&=&0.734\cdots \end{eqnarray}$$よって、\(r=0.73\) となり相関係数の値は変わらない

p.180 問2　相関係数 \(0.71\)
→ 相関係数

p.181 問3中央値 \(9.5\) 点
外れ値の影響を受けていない

p.185 問1① 紙の書籍と電子書籍のとちらが読みやすいか。
② 学年とコースが同じであるＡ組とＢ組の３５人ずつに、ある作家のエッセイをＡ組は紙の書籍でＢ組には電子書籍で読み終わるまでに掛かった時間を計測する実験を計画。
③ 実験を行い、読むのに掛かった時間を秒単位で回答してもらった。また、誤記と思われる回答の値を小さい順に並べて度数分布表に整理した。
④ 組ごとに結果をヒストグラムで表して、グラフを比較する。

p.185 問2電子書籍の方がデータの散らばりが大きい

p.186 問3\({\small (1)}~\)電力需要実績の最高気温、平均気温、日照時間のそれぞれの散布図を作り、相関を調べる。
\({\small (2)}~\)

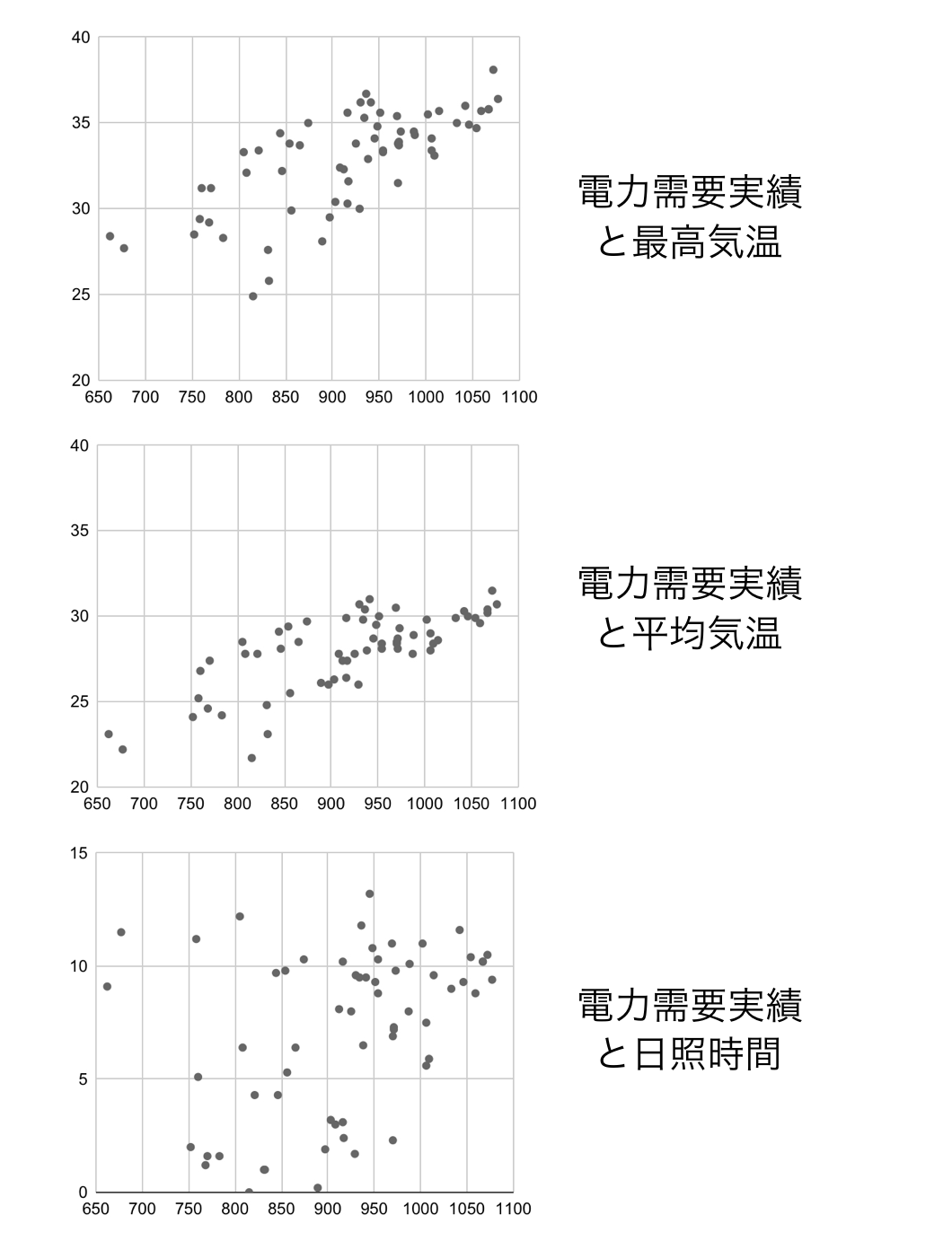
電力需要実績と平均気温の相関が一番大きい

p.187 問4\({\small (1)}~\)平日と休日それぞれの電力需要実績のヒストグラムを作り、データの散らばりを調べる。
\({\small (2)}~\)

平日の方が休日より電力需要実績の度合いが大きい

p.187 問5

平日の相関係数 \(0,92\)
休日の相関係数 \(0.93\)

p.191 問1味の違いが分かるという主張は誤りであると判断できない