【新課程】東京書籍：Advanced数学Ⅲ[701]

p.6 問1

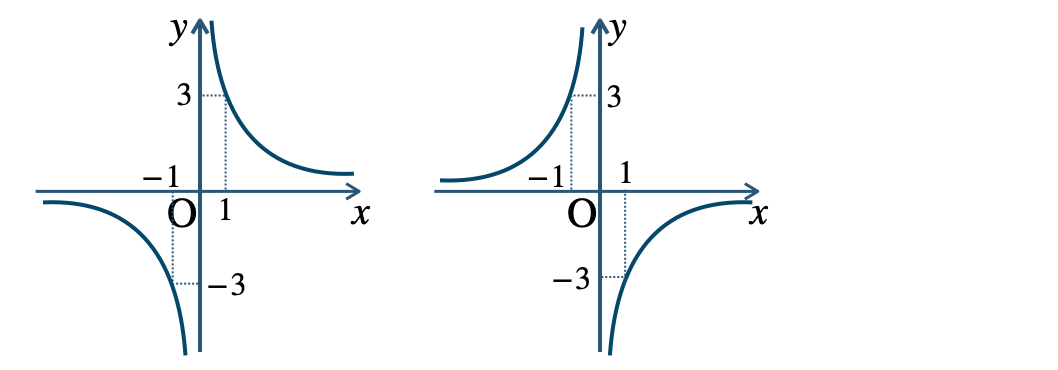
p.7 問2\({\small (1)}~\)漸近線 \(x=-3~,~y=-1\)

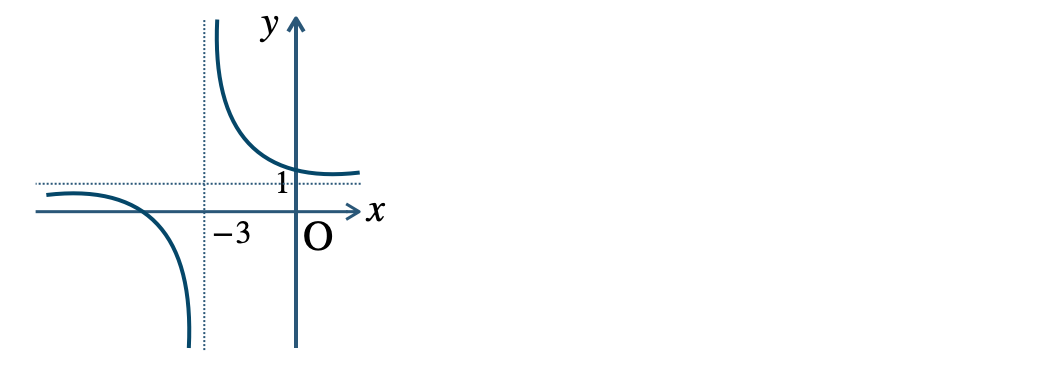
\({\small (2)}~\)漸近線 \(x=2~,~y=-5\)

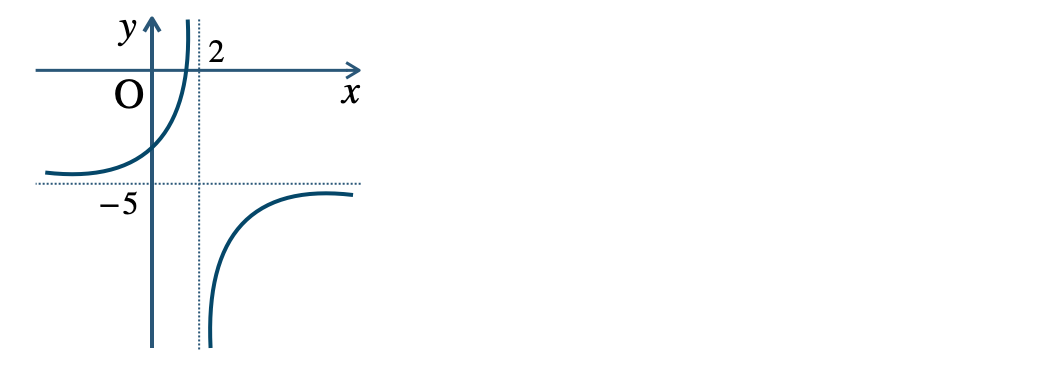
p.8 問3\({\small (1)}~\)漸近線 \(x=2~,~y=3\)

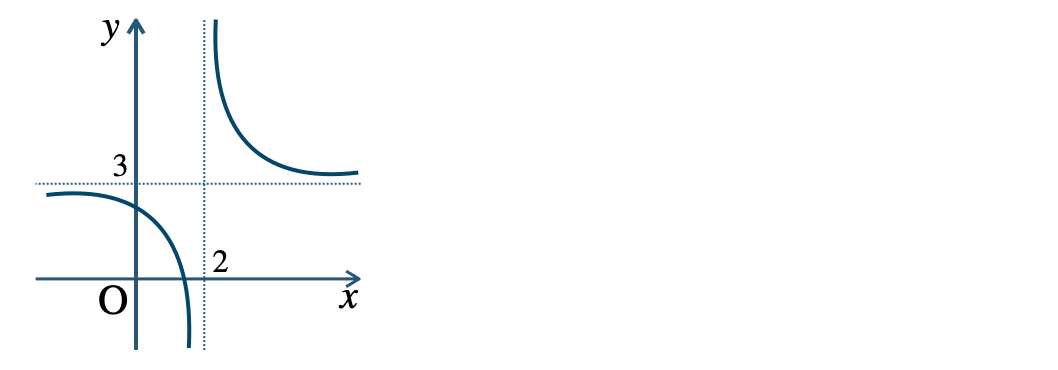
\({\small (2)}~\)漸近線 \(x=-2~,~y=2\)

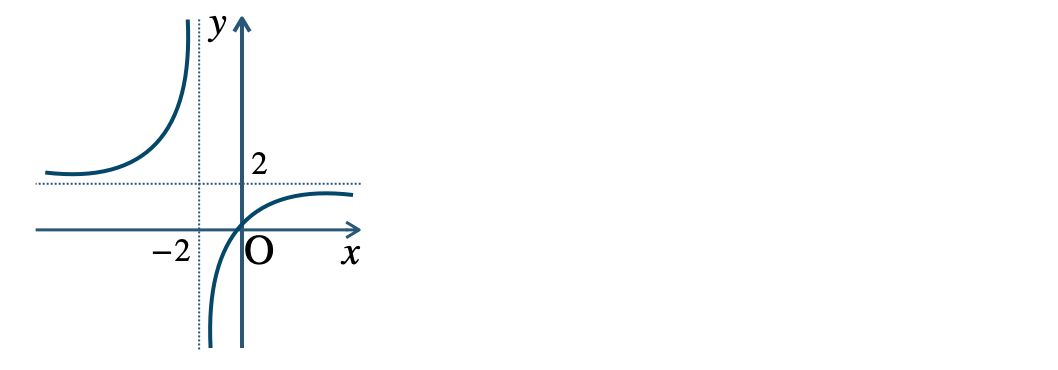
\({\small (3)}~\)漸近線 \(x={\large \frac{\,1\,}{\,2\,}}~,~y=-1\)

p.9 問4$${\small (1)}~0< x < 1~,~2< x$$$${\small (2)}~x< -2~,~-1≦x≦1$$

p.10 問5$${\small (1)}~x≧-\frac{\,2\,}{\,3\,}$$$${\small (2)}~x≦\frac{\,3\,}{\,2\,}$$

p.11 問6\({\small (1)}~\)

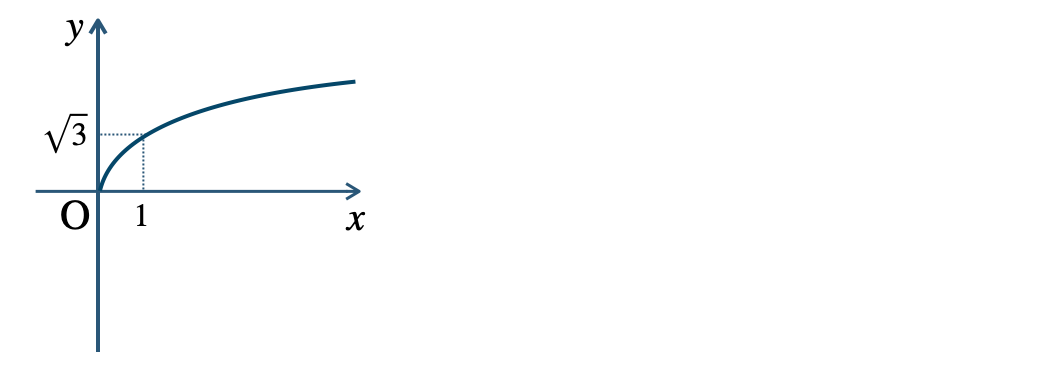
\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

p.12 問7\({\small (1)}~\)

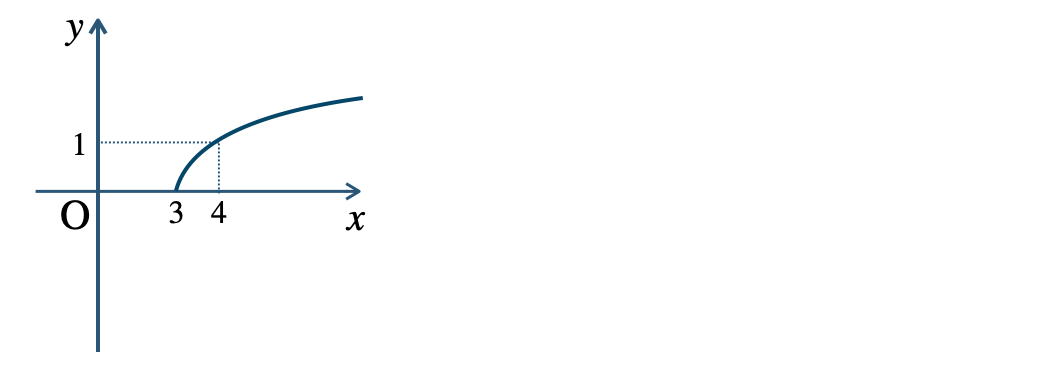
\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

p.13 問8$${\small (1)}~-\frac{\,5\,}{\,2\,}≦x < 10$$$${\small (2)}~x≦ -1$$

p.15 問9$${\small (1)}~y=-\frac{\,1\,}{\,3\,}x+\frac{\,2\,}{\,3\,}$$$${\small (2)}~y=\frac{\,2x-1\,}{\,x-2\,}$$

p.15 問10$${\small (1)}~y=3^x$$$${\small (2)}~y=\log_{\frac{\,1\,}{\,2\,}}x$$$${\small (3)}~y=2^x-1$$

p.16 問11$${\small (1)}~y=\sqrt{x+9}$$$${\small (2)}~y=-\sqrt{2x+4}$$

p.17 問12$${\small (1)}~y=-x^2+4~~~(x≦0)$$

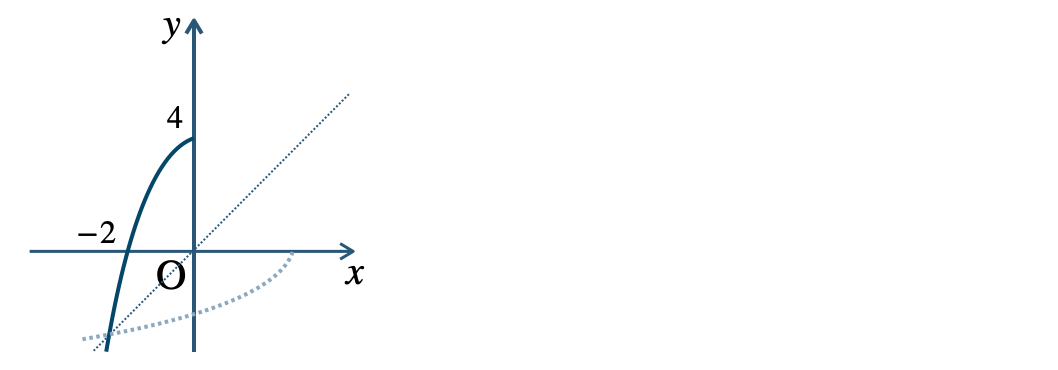
$${\small (2)}~y=\left( \frac{\,1\,}{\,2\,} \right)^x$$

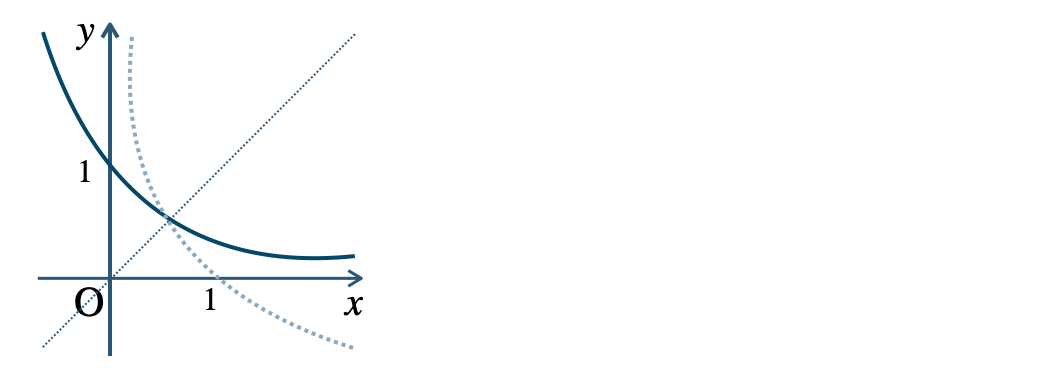
$${\small (3)}~y=\log_{3}(-x)$$

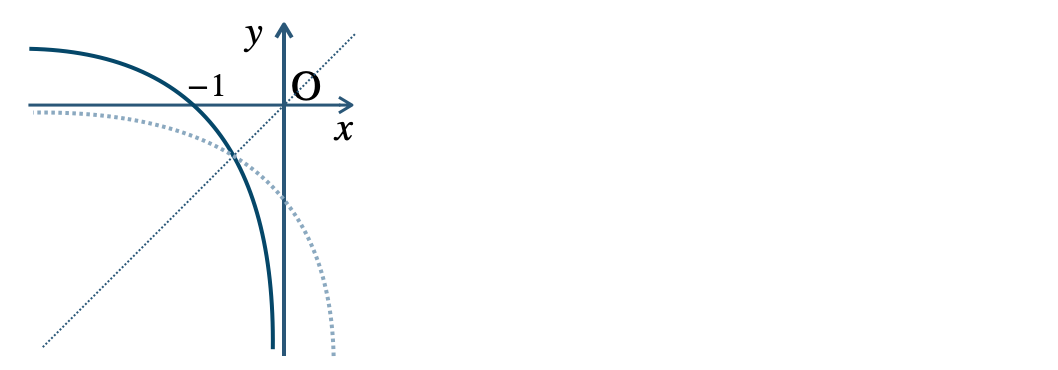
p.18 問13$${\small (1)}~(g\circ f)(x)=-2x^2-\frac{\,1\,}{\,2\,}$$$${\small (2)}~(f\circ g)(x)=(x+1)^2$$

p.19 問14$$~~~(g\circ f)(x)=x~,~(f\circ g)(x)=x$$

p.23 問1\({\small (1)}~\)正の無限大に発散
\({\small (2)}~2\) に収束
\({\small (3)}~\)負の無限大に発散
\({\small (4)}~\)発散(振動)

p.25 問2$${\small (1)}~0$$$${\small (2)}~\infty$$$${\small (3)}~\frac{\,1\,}{\,2\,}$$$${\small (4)}~0$$$${\small (5)}~-\frac{\,1\,}{\,2\,}$$$${\small (6)}~\frac{\,5\,}{\,3\,}$$

p.24 問31$${\small (1)}~-\infty$$$${\small (2)}~\infty$$$${\small (3)}~0$$$${\small (4)}~-1$$$${\small (5)}~3$$$${\small (6)}~2$$

p.27 問4$$~~~0$$

p.29 問5\({\small (1)}~0\)
\({\small (2)}~\)極限は存在しない(振動する)
\({\small (3)}~0\)
\({\small (4)}~-\infty\)

p.30 問6$${\small (1)}~0$$$${\small (2)}~1$$$${\small (3)}~4$$

p.30 問7\({\small (1)}~\)
\(~~~[1]~ 0< r< 1\) のとき、\(0\)
\(~~~[2]~ r=1\) のとき、\(1\)
\(~~~[3]~ r> 1\) のとき、\(3\)
\({\small (2)}~\)
\(~~~[1]~ | r|< 1\) のとき、\(1\)
\(~~~[2]~ r=1\) のとき、\(0\)
\(~~~[3]~ |r|> 1\) のとき、\(-1\)

p.31 問8$$~~~\lim_{n \to\infty}a_n=\frac{\,3\,}{\,2\,}$$

p.33 問9\({\small (1)}~\)収束、和は \({\large \frac{\,1\,}{\,2\,}}\)
\({\small (2)}~\)発散

p.35 問10\({\small (1)}~\)収束、和は \(128\)
\({\small (2)}~\)発散
\({\small (3)}~\)収束、和は \({\large \frac{\,10\,}{\,11\,}}\)

p.35 問11\({\small (1)}~-3< x < 3\) のとき、$$~~~\frac{\,3\,}{\,3-x\,}$$\({\small (2)}~0< x < 2\) のとき、$$~~~\frac{\,4\,}{\,x\,}$$

p.36 問12$$~~~\frac{\,2\sqrt{3}-1\,}{\,11\,}a^2$$

p.37 問13$${\small (1)}~\frac{\,2\,}{\,3\,}$$$${\small (2)}~\frac{\,10\,}{\,37\,}$$$${\small (3)}~\frac{\,234\,}{\,55\,}$$

p.38 問14$${\small (1)}~\frac{\,3\,}{\,4\,}$$$${\small (2)}~\frac{\,13\,}{\,8\,}$$

p.39 問15一般項は、$$\begin{eqnarray}~~~a_n&=&\frac{\,1+2+3+\cdots n\,}{\,n^2\,}\\[2pt]~~~&=&\frac{\,n(n+1)\,}{\,2n^2\,}\\[2pt]~~~&=&\frac{\,1\,}{\,2\,}+\frac{\,1\,}{\,2n\,}\end{eqnarray}$$よって、一般項の極限は、$$~~~\lim_{n\to\infty}a_n=\frac{\,1\,}{\,2\,}$$よって、\(0\) に収束しないので無限級数は発散する

p.43 問1$${\small (1)}~5$$$${\small (2)}~3$$

p.43 問2$${\small (1)}~-3$$$${\small (2)}~-\frac{\,1\,}{\,4\,}$$$${\small (3)}~\frac{\,1\,}{\,4\,}$$$${\small (4)}~-\frac{\,1\,}{\,36\,}$$

p.44 問3$${\small (1)}~a=7~,~b=10$$$${\small (2)}~a=4~,~b=4\sqrt{2}$$

p.45 問4$$~~~-\infty$$

p.46 問5　\(3\) と \(-3\)

p.47 問6$${\small (1)}~1$$$${\small (2)}~0$$$${\small (3)}~-\frac{\,1\,}{\,4\,}$$

p.48 問7$$~~~-\frac{\,3\,}{\,2\,}$$

p.48 問8$${\small (1)}~\infty$$$${\small (2)}~-\infty$$$${\small (3)}~\infty$$

p.49 問9$${\small (1)}~0$$$${\small (2)}~-\infty$$$${\small (3)}~\infty$$

p.51 問10$${\small (1)}~0$$$${\small (2)}~0$$

p.53 問11$${\small (1)}~4$$$${\small (2)}~1$$$${\small (3)}~-2$$

p.53 問12$${\small (1)}~1$$$${\small (2)}~2$$

p.54 問13$$~~~\frac{\,1\,}{\,2r\,}$$

p.56 問14$${\small (1)}~(2~,~5)$$$${\small (2)}~[-3~,~4]$$$${\small (3)}~(-\infty~,~7]$$

p.57 問16$${\small (1)}~(-\infty~,~-2)~,~(-2~,~\infty)$$$${\small (2)}~(-\infty~,~-3)~,~(-3~,~0)$$$$~~~~~~~~~,~(0~,~3)~,~(3~,~\infty)$$$${\small (3)}~\left(-\infty~,~\frac{\,2\,}{\,3\,}\right]$$

p.57 問16　\(x=0\) で連続
　\(x=1\) で不連続

p.58 問17\({\small (1)}~\)最大値なし、最小値 \(-1\)
\({\small (2)}~\)最大値 \(-1\)、最小値 \(-3\)

p.59 問18[証明] \(f(x)=x-2\sin{x}-3\) とすると、\(f(x)\) は閉区間 \([0~,~\pi]\) で連続であり、$$~~~f(0)=-3<0$$$$~~~f(\pi)=\pi-3>0$$したがって、中間値の定理より方程式 \(f(x)=0\) は \(0< x < \pi\) の範囲に少なくとも１つの実数解をもつ [終]

p.60 問題 18[証明] \(f(x)=\log_{10}x-{\large \frac{\,x\,}{\,20\,}}\) とすると、\(f(x)\) は閉区間 \([10~,~10\sqrt{10}]\) で連続であり、$$~~~f(10)=\frac{\,1\,}{\,2\,}>0$$$$~~~f(10\sqrt{10})=\frac{\,3-\sqrt{10}\,}{\,2\,}<0$$したがって、中間値の定理より方程式 \(f(x)=0\) は \(10< x < 10\sqrt{10}\) の範囲に少なくとも１つの実数解をもつ [終]

p.60 問題 19[証明] \(a~,~b~,~c~,~d\) を実数として、３次方程式を \(ax^3+bx^2+cx+d=0\) として、
\(f(x)=ax^3+bx^2+cx+d\) とすると、\(f(x)\) は閉区間 \([-\infty~,~\infty]\) で連続であり、$$~~~f(x)=x^3\left(a+\frac{\,b\,}{\,x\,}+\frac{\,c\,}{\,x^2\,}+\frac{\,d\,}{\,x^3\,}\right)$$とすると、$$~~~\lim_{x\to\infty}f(x)=\infty > 0$$$$~~~\lim_{x\to-\infty}f(x)=-\infty < 0$$したがって、中間値の定理より方程式 \(f(x)=0\) は少なくとも１つの実数解をもつ [終]