東京書籍：Standard数学Ⅰ

2019.04.102022.03.29

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。

１章　数と式
２章　集合と論証
３章　２次関数
４章　図形と計量

５章　データの分析

p.163
問1

p.163
問2

p.164
問3
\(26.5\)

p.165
問4
中央値 \(26.5\)
最頻値 \(29\)
→ 平均値・中央値・最頻値

p.167
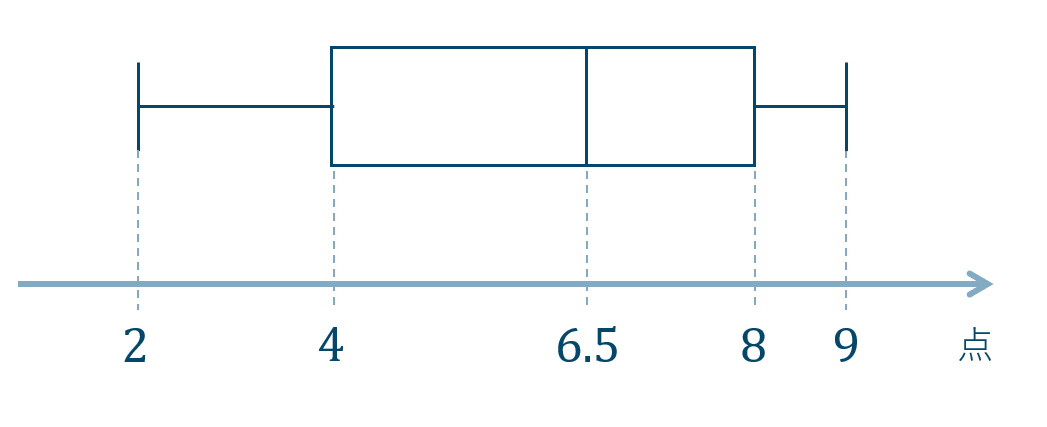
問5
１班
　第１四分位数 \(5.5\)
　第２四分位数 \(9.5\)
　第３四分位数 \(14.5\)
２班
　第１四分位数 \(1\)
　第２四分位数 \(9\)
　第３四分位数 \(18\)

p.168
問6

範囲 \(7\)
四分位範囲 \(4\)
四分位偏差 \(2\)
→ 箱ひげ図

p.169
問7
Ａ： \(\rm Y\)
Ｂ： \(\rm Z\)
Ｃ： \(\rm X\)

p.170
問8

２班の散らばりが大きい

p.172
問9
分散 \(64\)、標準偏差 \(8\)
→ 分散と標準偏差

Training

p.173
1
\({\small (1)}~\)

最頻値 \(35\)
\({\small (2)}~28.6\)

p.173
2
\({\small (1)}~\)

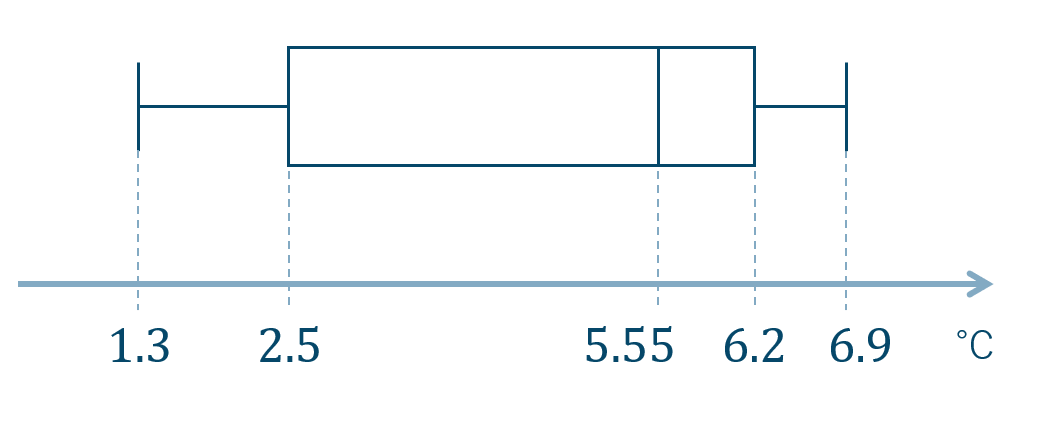
\({\small (2)}~{\rm D}\)

p.173
3
A \(2\)、B \(6.8\)

p.174
参考1
\(5.4\)

p.176
問1

p.179
問2
\(0.5\)
→ 相関係数

p.180
参考1

Training

p.181
1
図a：\(r=0.9\)
図b：\(r=0.6\)
図c：\(r=-0.8\)
図d：\(r=0\)

p.181
2
\({\small (1)}~\)Ａ：\(4\)　Ｂ：\(16\)　Ｃ：\(2\)　
Ｄ：\(4\)　Ｅ：\(8\)　Ｆ：\(0\)　Ｇ：\(0\)
\({\small (2)}~0.73\)

p.182
1
②と④

p.182
2
\({\small (1)}~10\)
\({\small (2)}~7\)
\({\small (3)}~\)②

p.182
3
\({\small (1)}~{\rm A}=100~,~{\rm B}=-9\)
\({\small (2)}~0.47\)
\({\small (3)}~x\) の分散：③
　\(x\) と \(y\) の相関係数：①