文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
資料 集合
p.156
問1
\(5\in {\rm A}~,~6\notin {\rm A}\)
問1
\(5\in {\rm A}~,~6\notin {\rm A}\)
p.157
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{-2,2\}\)
\({\small (3)}~\{5,10,15,20\cdots\}\)
→ 集合の表し方と要素
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{-2,2\}\)
\({\small (3)}~\{5,10,15,20\cdots\}\)
→ 集合の表し方と要素
p.157
問3
\({\rm A}\)、\({\rm C}\)
問3
\({\rm A}\)、\({\rm C}\)
p.158
問4
\({\small (1)}~\)
\({\rm A\cap B}=\{1,3,5\}\)
\({\rm A\cup B}=\{1,2,3,4,5,6,7\}\)
\({\small (2)}~\)
\({\rm A\cap B}=\{1,2,4,8\}\)
\({\rm A\cup B}=\{1,2,3,4,6,8,12,16,24,32\}\)
\({\small (3)}~\)
\({\rm A\cap B}=\{3\}\)
\({\rm A\cup B}=\{1,3,4,5,7,9\}\)
→ 共通部分と和集合
問4
\({\small (1)}~\)
\({\rm A\cap B}=\{1,3,5\}\)
\({\rm A\cup B}=\{1,2,3,4,5,6,7\}\)
\({\small (2)}~\)
\({\rm A\cap B}=\{1,2,4,8\}\)
\({\rm A\cup B}=\{1,2,3,4,6,8,12,16,24,32\}\)
\({\small (3)}~\)
\({\rm A\cap B}=\{3\}\)
\({\rm A\cup B}=\{1,3,4,5,7,9\}\)
→ 共通部分と和集合
p.159
問5
\({\small (1)}~\phi~,~\{3\}~,~\{4\}~,~\{3,4\}\)
\({\small (2)}~\phi~,~\{5\}~,~\{6\}~,~\{7\}\)
\(\{5,6\}~,~\{6,7\}~,~\{5,7\}~,~\{5,6,7\}\)
→ 集合の包含関係と部分集合
問5
\({\small (1)}~\phi~,~\{3\}~,~\{4\}~,~\{3,4\}\)
\({\small (2)}~\phi~,~\{5\}~,~\{6\}~,~\{7\}\)
\(\{5,6\}~,~\{6,7\}~,~\{5,7\}~,~\{5,6,7\}\)
→ 集合の包含関係と部分集合
p.159
問6
\({\small (1)}~{\rm \overline {A}}=\{1,3,5,7,8,9\}\)
\({\small (2)}~{\rm \overline {B}}=\{2,5,6,8,9\}\)
\({\small (3)}~{\rm \overline {A}\cap \overline {B}}=\{5,8,9\}\)
\({\small (4)}~{\rm \overline {A\cup B}}=\{5,8,9\}\)
問6
\({\small (1)}~{\rm \overline {A}}=\{1,3,5,7,8,9\}\)
\({\small (2)}~{\rm \overline {B}}=\{2,5,6,8,9\}\)
\({\small (3)}~{\rm \overline {A}\cap \overline {B}}=\{5,8,9\}\)
\({\small (4)}~{\rm \overline {A\cup B}}=\{5,8,9\}\)
p.160
問7
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、

この2つの和集合となるので、

これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
→ 補集合とド・モルガンの法則
問7
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、
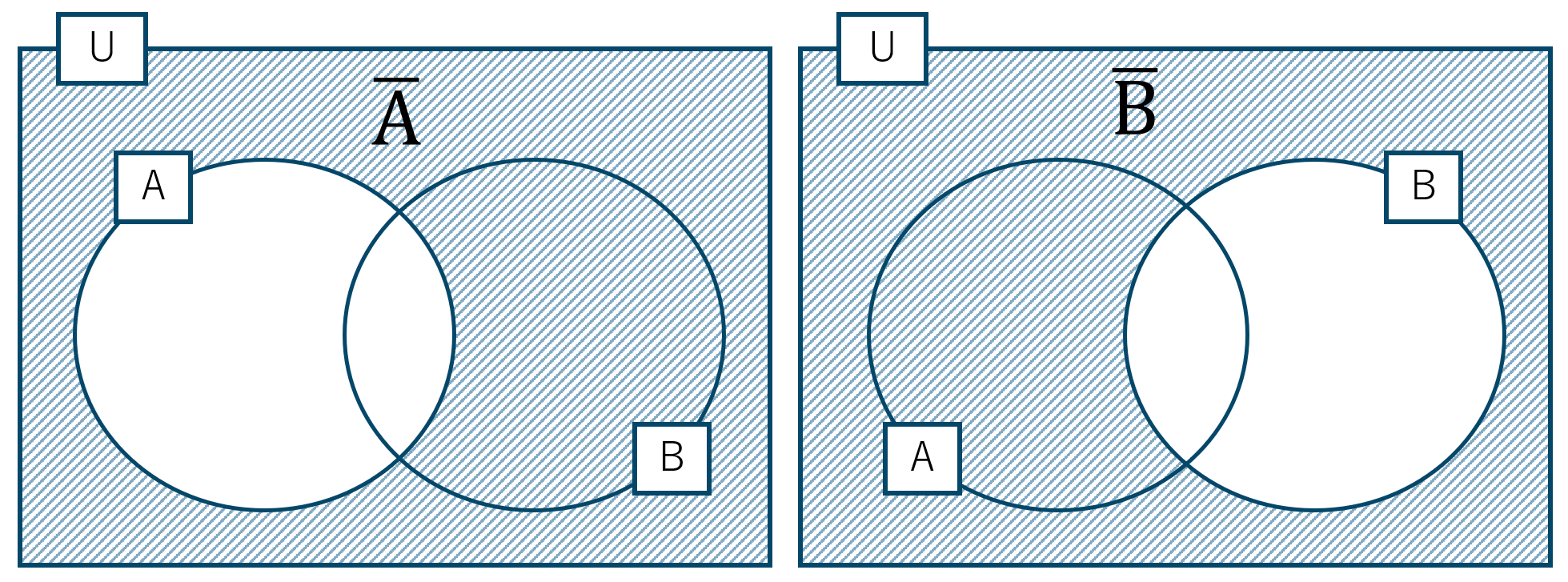
この2つの和集合となるので、
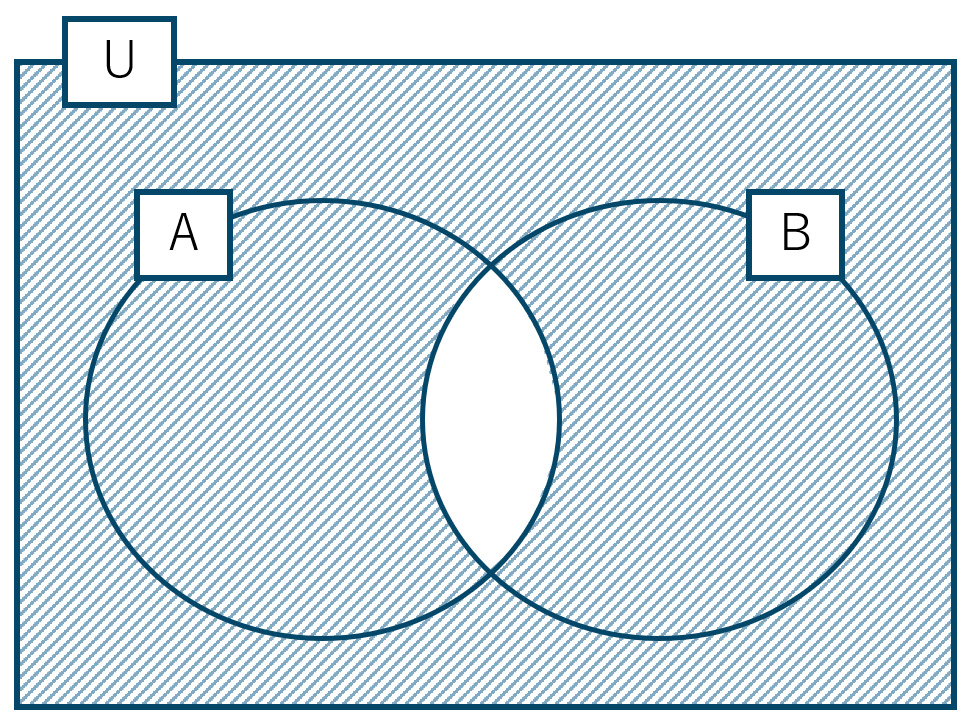
これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
→ 補集合とド・モルガンの法則
Training
p.161
1
\({\small (1)}~{\rm A}\cap{\rm B}=\{x~|~5<x≦7\}\)
\({\small (2)}~{\rm A}\cup{\rm B}=\{x~|~3≦x<10\}\)
\({\small (3)}~{\rm \overline {A}}\cap{\rm \overline {B}}=\{x~|~x≦5~,~7<x\}\)
\({\small (4)}~{\rm \overline {A}}\cup{\rm \overline {B}}=\{x~|~x<3~,~10≦x\}\)
→ 数直線と集合
1
\({\small (1)}~{\rm A}\cap{\rm B}=\{x~|~5<x≦7\}\)
\({\small (2)}~{\rm A}\cup{\rm B}=\{x~|~3≦x<10\}\)
\({\small (3)}~{\rm \overline {A}}\cap{\rm \overline {B}}=\{x~|~x≦5~,~7<x\}\)
\({\small (4)}~{\rm \overline {A}}\cup{\rm \overline {B}}=\{x~|~x<3~,~10≦x\}\)
→ 数直線と集合
p.161
2
\({\small (1)}~{\rm B}=\{2,4,6,7,8,9\}\)
\({\small (2)}~{\rm A}\cap{\rm \overline {B}}=\{1,3\}\)
\({\small (3)}~{\rm A \cup \overline {B}}=\{1,3,4,5,6,8,10\}\)
\({\small (4)}~{\rm \overline {\overline {A} \cap B}}=\{1,3,4,5,6,8,10\}\)
2
\({\small (1)}~{\rm B}=\{2,4,6,7,8,9\}\)
\({\small (2)}~{\rm A}\cap{\rm \overline {B}}=\{1,3\}\)
\({\small (3)}~{\rm A \cup \overline {B}}=\{1,3,4,5,6,8,10\}\)
\({\small (4)}~{\rm \overline {\overline {A} \cap B}}=\{1,3,4,5,6,8,10\}\)


