文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
3章 図形の性質
Readiness check
p.106
問1
\(x=60^\circ~,~y=105^\circ\)
問1
\(x=60^\circ~,~y=105^\circ\)
p.106
問2
\(x=23^\circ\)
問2
\(x=23^\circ\)
p.106
問3
\(\triangle {\rm ABC} \equiv \triangle {\rm JLK}\)
→1組の辺とその両端の角がそれぞれ等しい
\(\triangle {\rm DEF} \equiv \triangle {\rm NOM}\)
→3組の辺がそれぞれ等しい
\(\triangle {\rm GHI} \equiv \triangle {\rm PRQ}\)
→2組の辺とその間の角がそれぞれ等しい
問3
\(\triangle {\rm ABC} \equiv \triangle {\rm JLK}\)
→1組の辺とその両端の角がそれぞれ等しい
\(\triangle {\rm DEF} \equiv \triangle {\rm NOM}\)
→3組の辺がそれぞれ等しい
\(\triangle {\rm GHI} \equiv \triangle {\rm PRQ}\)
→2組の辺とその間の角がそれぞれ等しい
p.107
問4
\(\triangle {\rm ABC} \equiv \triangle {\rm KJL}\)
→斜辺と1組の鋭角がそれぞれ等しい
\(\triangle {\rm DEF} \equiv \triangle {\rm IGH}\)
→斜辺と他の1組の辺がそれぞれ等しい
問4
\(\triangle {\rm ABC} \equiv \triangle {\rm KJL}\)
→斜辺と1組の鋭角がそれぞれ等しい
\(\triangle {\rm DEF} \equiv \triangle {\rm IGH}\)
→斜辺と他の1組の辺がそれぞれ等しい
p.107
問5
\({\small (1)}~75^\circ\) \({\small (2)}~40^\circ\)
問5
\({\small (1)}~75^\circ\) \({\small (2)}~40^\circ\)
p.107
問6
\(\triangle {\rm ABC}\sim\triangle {\rm JLK}\)
→2組の角がそれぞれ等しい
\(\triangle {\rm DEF}\sim\triangle {\rm MNO}\)
→2組の辺の比とその間の角がそれぞれ等しい
\(\triangle {\rm GHI}\sim\triangle {\rm QPR}\)
→3組の辺の比がそれぞれ等しい
問6
\(\triangle {\rm ABC}\sim\triangle {\rm JLK}\)
→2組の角がそれぞれ等しい
\(\triangle {\rm DEF}\sim\triangle {\rm MNO}\)
→2組の辺の比とその間の角がそれぞれ等しい
\(\triangle {\rm GHI}\sim\triangle {\rm QPR}\)
→3組の辺の比がそれぞれ等しい
1節 三角形と比
p.109
問2
\({\small (1)}~\)平行四辺形
\({\small (2)}~\)ひし形
問2
\({\small (1)}~\)平行四辺形
\({\small (2)}~\)ひし形
Training
p.121
1
\({\small (1)}~10\) \({\small (2)}~40\)
1
\({\small (1)}~10\) \({\small (2)}~40\)
p.121
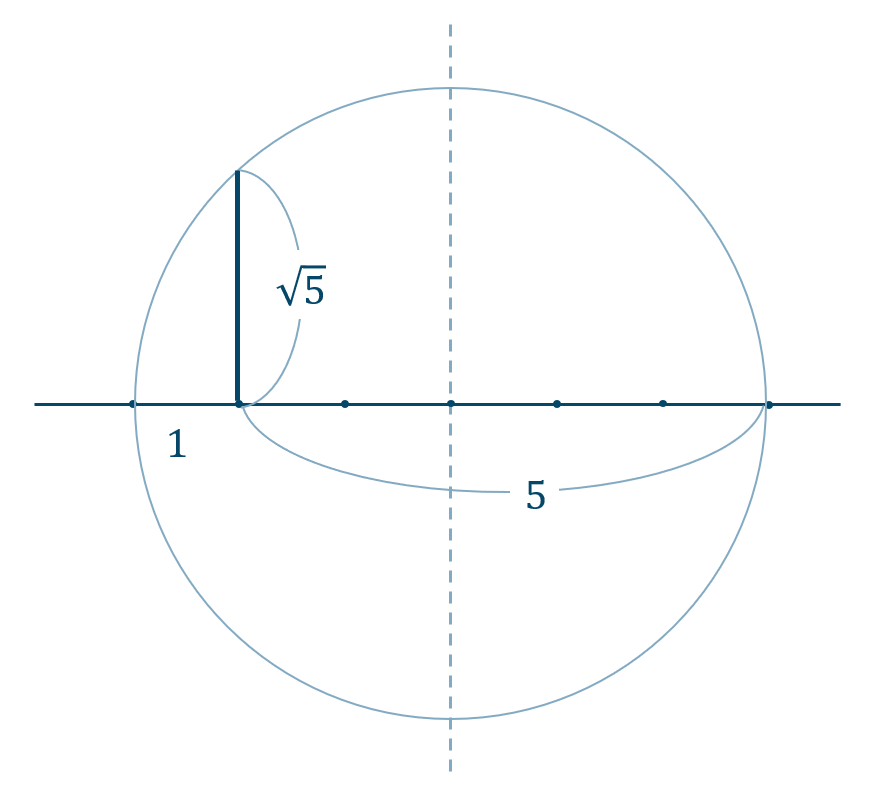
2
\({\small (1)}~{\large \frac{3\sqrt{2}}{2}}\) \({\small (2)}~{\large \frac{\sqrt{10}}{2}}\)
2
\({\small (1)}~{\large \frac{3\sqrt{2}}{2}}\) \({\small (2)}~{\large \frac{\sqrt{10}}{2}}\)
p.121
3
\({\small (1)}~130^\circ\) \({\small (2)}~115^\circ\)
3
\({\small (1)}~130^\circ\) \({\small (2)}~115^\circ\)
p.121
4
\({\small (1)}~30^\circ\) \({\small (2)}~125^\circ\)
4
\({\small (1)}~30^\circ\) \({\small (2)}~125^\circ\)
p.121
5
\({\small (1)}~4:9\)
\({\small (2)}~13:6\)
5
\({\small (1)}~4:9\)
\({\small (2)}~13:6\)
p.123
参考1
辺 \({\rm BC}\) と辺 \({\rm CA}\) の長さの和は、
\(2+3=5\)
これは、辺 \({\rm AB}\) の長さ \(6\) より小さい
よって、
\({\rm AB>BC+CA}\)
2辺の和が他の1辺の長さより大きくならないので、このような \(\triangle {\rm ABC}\) は存在しない
→ 三角形になるための条件
参考1
辺 \({\rm BC}\) と辺 \({\rm CA}\) の長さの和は、
\(2+3=5\)
これは、辺 \({\rm AB}\) の長さ \(6\) より小さい
よって、
\({\rm AB>BC+CA}\)
2辺の和が他の1辺の長さより大きくならないので、このような \(\triangle {\rm ABC}\) は存在しない
→ 三角形になるための条件
2節 円の性質
p.124
問1
\({\small (1)}~40^\circ\) \({\small (2)}~40^\circ\)
\({\small (3)}~220^\circ\)
問1
\({\small (1)}~40^\circ\) \({\small (2)}~40^\circ\)
\({\small (3)}~220^\circ\)
p.126
問4
\({\small (1)}~106^\circ\) \({\small (2)}~80^\circ\)
\({\small (3)}~100^\circ\)
→ 円に内接する四角形と角
問4
\({\small (1)}~106^\circ\) \({\small (2)}~80^\circ\)
\({\small (3)}~100^\circ\)
→ 円に内接する四角形と角
p.131
問9
[証明] 接弦定理より、
\(\angle{\rm ACB}=\angle{\rm BAD}\)
また、\({\rm AC=AD}\) より \(\triangle {\rm ACD}\) は二等辺三角形となり底角が等しいので、
\(\angle{\rm ACD}=\angle{\rm ADC}\)
よって、
\(\angle{\rm BAD}=\angle{\rm BDA}\)
底角が等しいので、\(\triangle {\rm BAD}\) は二等辺三角形となる
したがって、
\({\rm BA=BD}\) [終]
問9
[証明] 接弦定理より、
\(\angle{\rm ACB}=\angle{\rm BAD}\)
また、\({\rm AC=AD}\) より \(\triangle {\rm ACD}\) は二等辺三角形となり底角が等しいので、
\(\angle{\rm ACD}=\angle{\rm ADC}\)
よって、
\(\angle{\rm BAD}=\angle{\rm BDA}\)
底角が等しいので、\(\triangle {\rm BAD}\) は二等辺三角形となる
したがって、
\({\rm BA=BD}\) [終]
p.134
問12
\({\small (1)}~\)4本 \({\small (2)}~\)3本 \({\small (3)}~\)2本
\({\small (4)}~\)1本 \({\small (5)}~\)0本
→ 2つの円の位置関係と共通接線
問12
\({\small (1)}~\)4本 \({\small (2)}~\)3本 \({\small (3)}~\)2本
\({\small (4)}~\)1本 \({\small (5)}~\)0本
→ 2つの円の位置関係と共通接線
Training
p.136
6
\({\small (1)}~47^\circ\) \({\small (2)}~40^\circ\)
\({\small (3)}~83^\circ\)
6
\({\small (1)}~47^\circ\) \({\small (2)}~40^\circ\)
\({\small (3)}~83^\circ\)
p.136
7
\({\small (1)}~{\large \frac{21}{2}}\) \({\small (2)}~4\)
7
\({\small (1)}~{\large \frac{21}{2}}\) \({\small (2)}~4\)
p.136
8
\({\small (1)}~28^\circ\) \({\small (2)}~20^\circ\)
8
\({\small (1)}~28^\circ\) \({\small (2)}~20^\circ\)
p.136
9
\({\small (1)}~{\large \frac{5}{2}}\) \({\small (2)}~5\)
9
\({\small (1)}~{\large \frac{5}{2}}\) \({\small (2)}~5\)
p.136
10
\(2\sqrt{22}\)
10
\(2\sqrt{22}\)
3節 作図
p.137
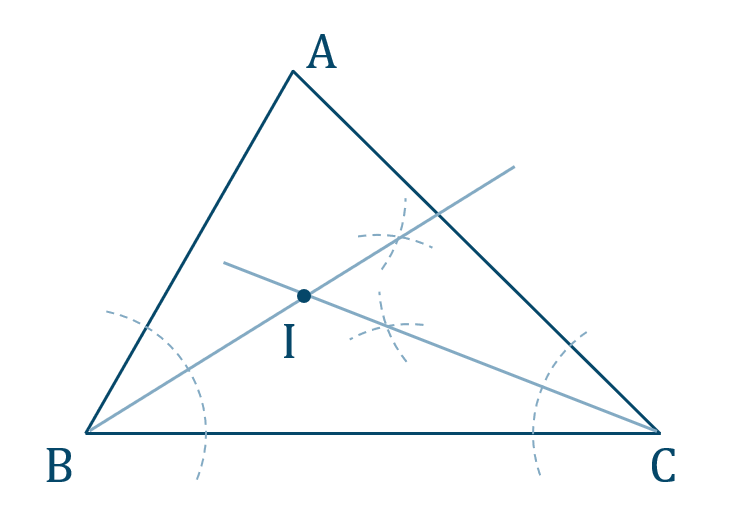
問1

問1
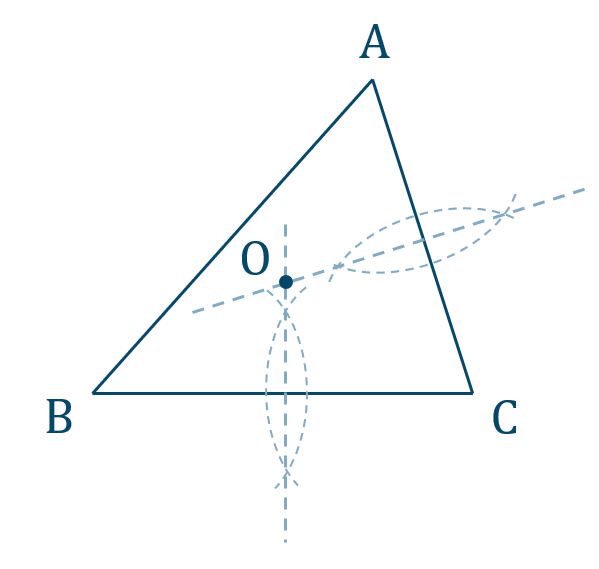
p.137
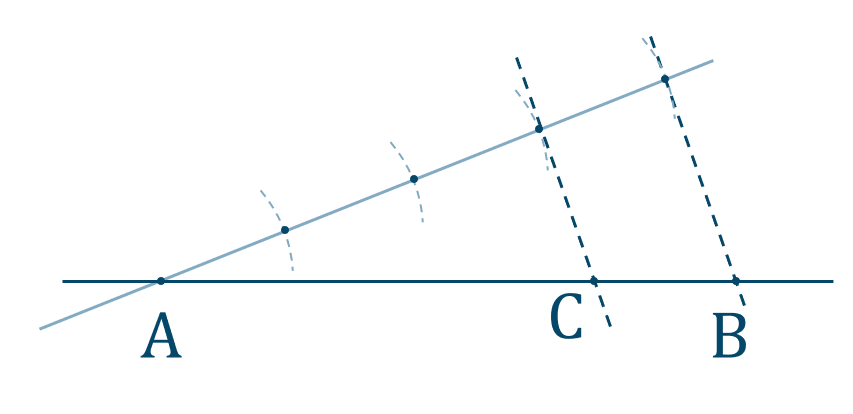
問2

問2
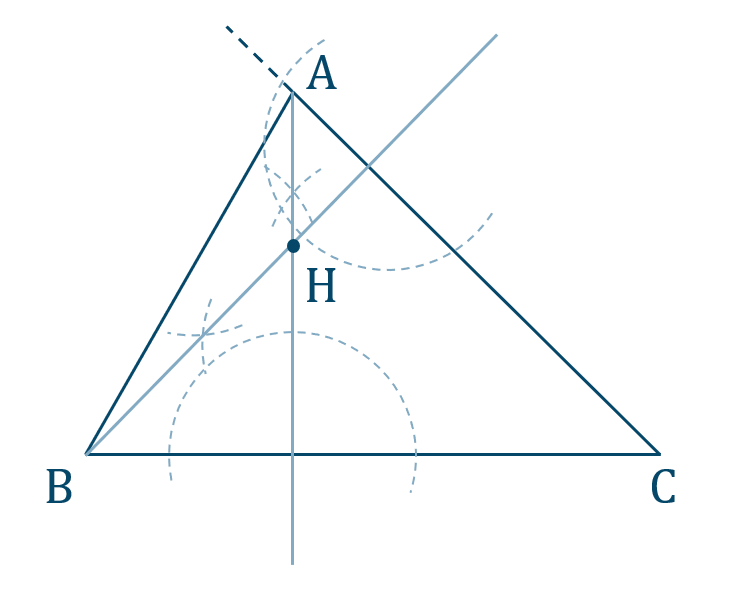
Training
p.142
11

11
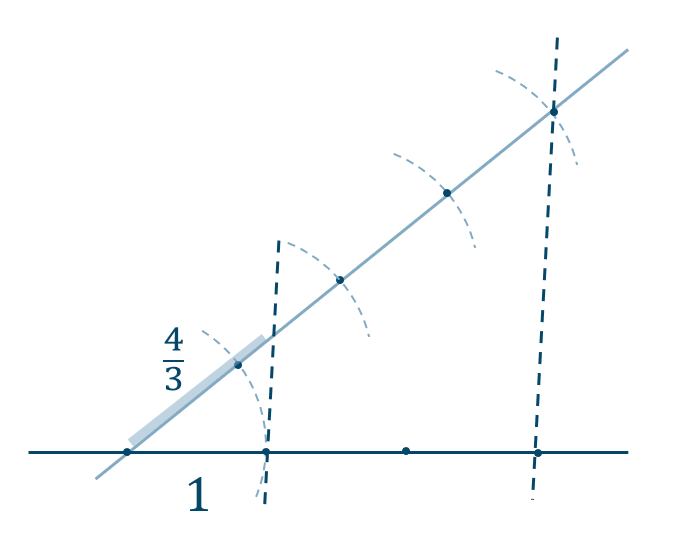
p.142
12

12

p.142
13

13
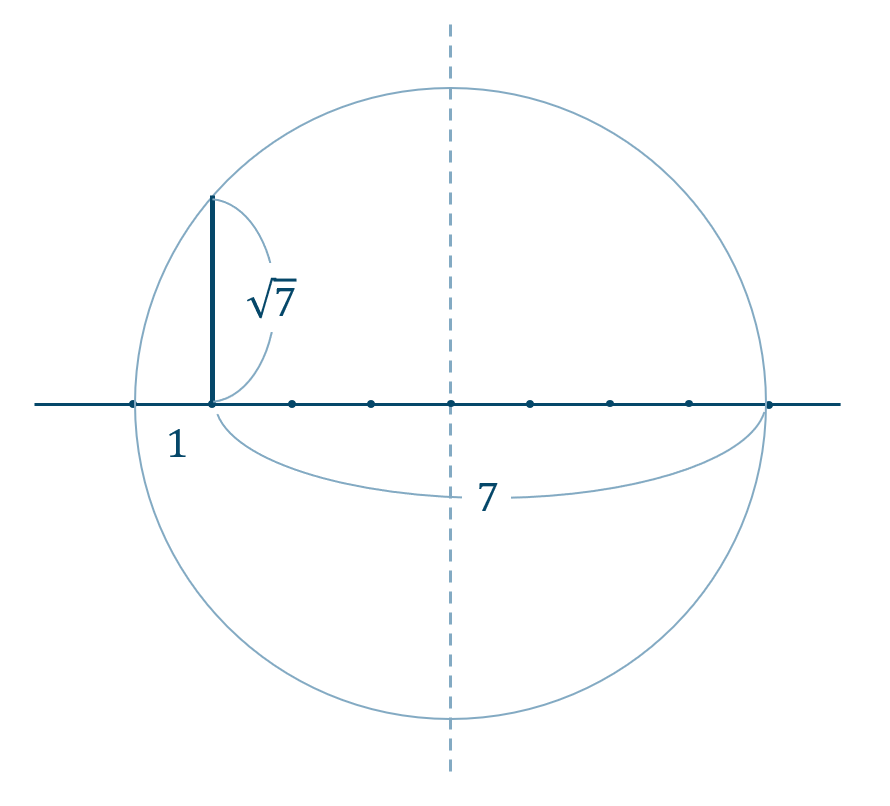
4節 空間図形
p.143
問1
\({\small (1)}~90^\circ\) \({\small (2)}~45^\circ\)
\({\small (3)}~90^\circ\)
問1
\({\small (1)}~90^\circ\) \({\small (2)}~45^\circ\)
\({\small (3)}~90^\circ\)
p.146
問3
[証明] \(\triangle {\rm OAB}\) において、
\({\rm OA=OC}\) の二等辺三角形で、点 \({\rm P}\) は正方形 \({\rm ABCD}\) の対角線の交点より
\({\rm AP=CP}\)
よって、
\({\rm OP\perp AC}\)
\(\triangle {\rm OBD}\) でも同様に考えて、
\({\rm OP\perp BD}\)
したがって、直線 \({\rm OP}\) は面 \({\rm ABCD}\) 上の2直線 \({\rm AC~,~BD}\) に垂直であるので、
平面 \({\rm ABCD\perp OP}\) [終]
問3
[証明] \(\triangle {\rm OAB}\) において、
\({\rm OA=OC}\) の二等辺三角形で、点 \({\rm P}\) は正方形 \({\rm ABCD}\) の対角線の交点より
\({\rm AP=CP}\)
よって、
\({\rm OP\perp AC}\)
\(\triangle {\rm OBD}\) でも同様に考えて、
\({\rm OP\perp BD}\)
したがって、直線 \({\rm OP}\) は面 \({\rm ABCD}\) 上の2直線 \({\rm AC~,~BD}\) に垂直であるので、
平面 \({\rm ABCD\perp OP}\) [終]
p.147
問4
\({\small (1)}~\)[証明] 直線 \(l\) は \(\alpha\) 上にあるので、\({\rm PO}\perp\alpha\) より、
\({\rm PO}\perp l\)
また、仮定より
\({\rm OA}\perp l\)
ここで、平面 \({\rm PAO}\) 上の2直線に垂直であるので、
\(l\perp\) 平面 \({\rm PAO}\)
したがって、平面 \({\rm PAO}\) 上の直線 \({\rm PA}\) に対しても \({\rm PA}\perp l\) [終]
\({\small (2)}~\)[証明] 直線 \(l\) は平面 \(\alpha\) 上にあり、
\({\rm PO}\perp \alpha\) より \({\rm PO}\perp l\)
また、仮定より \({\rm PA}\perp l\)
よって、平面 \({\rm PAO}\) 上の2直線に垂直であるので、
\(l\perp \) 平面 \({\rm PAO}\)
したがって、平面 \({\rm PAO}\) 上の直線 \({\rm OA}\) に対しても \({\rm OA}\perp l\) [終]
問4
\({\small (1)}~\)[証明] 直線 \(l\) は \(\alpha\) 上にあるので、\({\rm PO}\perp\alpha\) より、
\({\rm PO}\perp l\)
また、仮定より
\({\rm OA}\perp l\)
ここで、平面 \({\rm PAO}\) 上の2直線に垂直であるので、
\(l\perp\) 平面 \({\rm PAO}\)
したがって、平面 \({\rm PAO}\) 上の直線 \({\rm PA}\) に対しても \({\rm PA}\perp l\) [終]
\({\small (2)}~\)[証明] 直線 \(l\) は平面 \(\alpha\) 上にあり、
\({\rm PO}\perp \alpha\) より \({\rm PO}\perp l\)
また、仮定より \({\rm PA}\perp l\)
よって、平面 \({\rm PAO}\) 上の2直線に垂直であるので、
\(l\perp \) 平面 \({\rm PAO}\)
したがって、平面 \({\rm PAO}\) 上の直線 \({\rm OA}\) に対しても \({\rm OA}\perp l\) [終]
p.148
問5
頂点 \(4~,~8~,~6~,~(20)~,~12\)
辺 \(6~,~12~,~12~,~(30)~,~30\)
問5
頂点 \(4~,~8~,~6~,~(20)~,~12\)
辺 \(6~,~12~,~12~,~(30)~,~30\)
p.149
参考1
\(v\) は \(3\) 増加する
\(e\) は \(4\) 増加する
\(f\) は \(1\) 増加する
また、
\(3-4+1=0\)
これより、\(v-e+f\) は変化しない
参考1
\(v\) は \(3\) 増加する
\(e\) は \(4\) 増加する
\(f\) は \(1\) 増加する
また、
\(3-4+1=0\)
これより、\(v-e+f\) は変化しない
Training
p.151
14
[証明] \(\triangle {\rm ABD}\) において、
\({\rm AP:AB=AS:AD}=2:3\) であり、平行線と線分の比の関係より、
\({\rm PS\parallel BD}\)
\({\rm PS:BD}=2:3\)
次に、\(\triangle {\rm CBD}\) において、
\({\rm CQ:CB=CR:CD}=2:3\) であり、平行線と線分の比の関係より、
\({\rm QR\parallel BD}\)
\({\rm QR:BD}=2:3\)
これらより、
\({\rm PS\parallel QR}\)
\({\rm PS=QR}\)
1組の対辺が平行で等しいので、四角形 \({\rm PQRS}\) は平行四辺形である [終]
14
[証明] \(\triangle {\rm ABD}\) において、
\({\rm AP:AB=AS:AD}=2:3\) であり、平行線と線分の比の関係より、
\({\rm PS\parallel BD}\)
\({\rm PS:BD}=2:3\)
次に、\(\triangle {\rm CBD}\) において、
\({\rm CQ:CB=CR:CD}=2:3\) であり、平行線と線分の比の関係より、
\({\rm QR\parallel BD}\)
\({\rm QR:BD}=2:3\)
これらより、
\({\rm PS\parallel QR}\)
\({\rm PS=QR}\)
1組の対辺が平行で等しいので、四角形 \({\rm PQRS}\) は平行四辺形である [終]
p.151
15
\({\small (1)}~60^\circ\) \({\small (2)}~45^\circ\)
\({\small (3)}~90^\circ\)
15
\({\small (1)}~60^\circ\) \({\small (2)}~45^\circ\)
\({\small (3)}~90^\circ\)
p.151
16
\({\small (1)}~45^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~90^\circ\)
16
\({\small (1)}~45^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~90^\circ\)
p.151
17
\({\small (1)}~\)[証明]正方形 \({\rm ABCD}\) の対角線は直交するので、
\({\rm AC\perp BD}\) …①
\({\rm AE\parallel BF}\) で四角形 \({\rm BFHD}\) が長方形より、\({\rm BD}\) と \({\rm BF}\) のなす角が \(90^\circ\)となり、 \({\rm BD}\) と \({\rm AE}\) のなす角が \(90^\circ\) となるので、
\({\rm AE\perp BD}\) …②
よって、\({\rm AC~,~AE}\) は平面 \({\rm AECG}\) 上の直線であり、①と②より直線 \({\rm BD}\) はこの2直線にそれぞれ直交する
したがって
直線 \({\rm BD}\) \(\perp\) 平面 \({\rm AEGC}\) [終]
\({\small (2)}~\)[証明] (1) より、平面 \({\rm AEGC}\) 上のすべての直線が直線 \({\rm BD}\) と垂直であるので、
\({\rm CE\perp BD}\) [終]
17
\({\small (1)}~\)[証明]正方形 \({\rm ABCD}\) の対角線は直交するので、
\({\rm AC\perp BD}\) …①
\({\rm AE\parallel BF}\) で四角形 \({\rm BFHD}\) が長方形より、\({\rm BD}\) と \({\rm BF}\) のなす角が \(90^\circ\)となり、 \({\rm BD}\) と \({\rm AE}\) のなす角が \(90^\circ\) となるので、
\({\rm AE\perp BD}\) …②
よって、\({\rm AC~,~AE}\) は平面 \({\rm AECG}\) 上の直線であり、①と②より直線 \({\rm BD}\) はこの2直線にそれぞれ直交する
したがって
直線 \({\rm BD}\) \(\perp\) 平面 \({\rm AEGC}\) [終]
\({\small (2)}~\)[証明] (1) より、平面 \({\rm AEGC}\) 上のすべての直線が直線 \({\rm BD}\) と垂直であるので、
\({\rm CE\perp BD}\) [終]
p.151
18
[証明] \({\rm \triangle {\rm ACD}}\) は正三角形であり、点 \({\rm M}\) は線分 \({\rm CD}\) の中点であるので、
\({\rm AM\perp CD}\)
次に、\({\rm \triangle {\rm BCD}}\) は正三角形であり、点 \({\rm M}\) は線分 \({\rm CD}\) の中点であるので、
\({\rm BM\perp CD}\)
仮定より
\({\rm AH\perp BM}\)
したがって、三垂線の定理より
\({\rm AH} \perp\) 平面 \({\rm BCD}\) [終]
18
[証明] \({\rm \triangle {\rm ACD}}\) は正三角形であり、点 \({\rm M}\) は線分 \({\rm CD}\) の中点であるので、
\({\rm AM\perp CD}\)
次に、\({\rm \triangle {\rm BCD}}\) は正三角形であり、点 \({\rm M}\) は線分 \({\rm CD}\) の中点であるので、
\({\rm BM\perp CD}\)
仮定より
\({\rm AH\perp BM}\)
したがって、三垂線の定理より
\({\rm AH} \perp\) 平面 \({\rm BCD}\) [終]
Level Up 図形の性質
p.152
1
\({\small (1)}~{\large \frac{7}{2}}\) \({\small (2)}~2:1\)
1
\({\small (1)}~{\large \frac{7}{2}}\) \({\small (2)}~2:1\)
p.152
2
\({\small (1)}~\)[証明]

図のように点 \({\rm J}\) から線分 \({\rm BC}\) に下ろした垂線を \({\rm JH}\) とすると、
\({\rm \triangle {\rm JBP}}\) と \({\rm \triangle {\rm JBH}}\) において、
共通な辺より、
\({\rm JB=JB}\)
仮定より、
\(\angle{\rm JBP}=\angle{\rm JBH}\)
斜辺と1組の角がそれぞれ等しいので、
\(\triangle {\rm JBP}\equiv\triangle {\rm JBH}\)
よって、
\({\rm JP=JH}\)
同様に、\({\rm \triangle {\rm JCQ}}\) と \({\rm \triangle {\rm JCH}}\) でも考えると、
\({\rm \triangle {\rm JCQ}\equiv\triangle {\rm JCH}}\)
よって、
\({\rm JQ=JH}\)
したがって、
\({\rm JP=JQ}\) [終]
\({\small (2)}~\)[証明] \({\rm \triangle {\rm APJ}}\) と \({\rm \triangle {\rm AQJ}}\) において、
\(\angle{\rm APJ}=\angle{\rm AQJ}=90^\circ\)
共通な辺より、
\({\rm AJ=AJ}\)
斜辺と他の1組の辺がそれぞれ等しいので、
\(\triangle {\rm APJ}\equiv\triangle {\rm AQJ}\)
対応する角が等しいので、
\(\angle{\rm JAP}=\angle{\rm JAQ}\)
したがって、点 \({\rm J}\) は \(\angle {\rm A}\) の二等分線上にある [終]
2
\({\small (1)}~\)[証明]
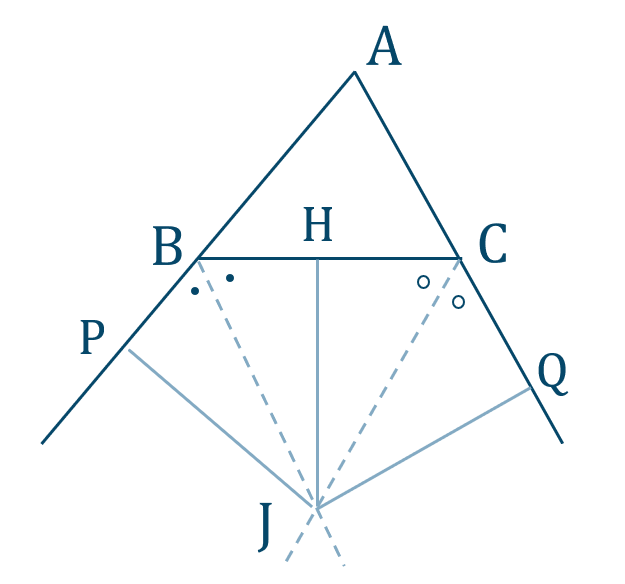
図のように点 \({\rm J}\) から線分 \({\rm BC}\) に下ろした垂線を \({\rm JH}\) とすると、
\({\rm \triangle {\rm JBP}}\) と \({\rm \triangle {\rm JBH}}\) において、
共通な辺より、
\({\rm JB=JB}\)
仮定より、
\(\angle{\rm JBP}=\angle{\rm JBH}\)
斜辺と1組の角がそれぞれ等しいので、
\(\triangle {\rm JBP}\equiv\triangle {\rm JBH}\)
よって、
\({\rm JP=JH}\)
同様に、\({\rm \triangle {\rm JCQ}}\) と \({\rm \triangle {\rm JCH}}\) でも考えると、
\({\rm \triangle {\rm JCQ}\equiv\triangle {\rm JCH}}\)
よって、
\({\rm JQ=JH}\)
したがって、
\({\rm JP=JQ}\) [終]
\({\small (2)}~\)[証明] \({\rm \triangle {\rm APJ}}\) と \({\rm \triangle {\rm AQJ}}\) において、
\(\angle{\rm APJ}=\angle{\rm AQJ}=90^\circ\)
共通な辺より、
\({\rm AJ=AJ}\)
斜辺と他の1組の辺がそれぞれ等しいので、
\(\triangle {\rm APJ}\equiv\triangle {\rm AQJ}\)
対応する角が等しいので、
\(\angle{\rm JAP}=\angle{\rm JAQ}\)
したがって、点 \({\rm J}\) は \(\angle {\rm A}\) の二等分線上にある [終]
p.152
3
\(3:8\)
3
\(3:8\)
p.152
4
[証明]

図のように、直線 \({\rm CD}\) の延長線上に点 \({\rm P}\) をとると、
\({\rm AD\parallel BC}\) の同位角より、
\(\angle{\rm ADP}=\angle{\rm BCF}\) …①
四角形 \({\rm EBCF}\) は円に内接しているので、外角の条件より、
\(\angle{\rm BCF}=\angle{\rm AEF}\) …②
①、②より、
\(\angle{\rm ADP}=\angle{\rm AEF}\)
四角形 \({\rm AEFD}\) において、1つの外角が隣り合う内角の対角に等しいので、四角形 \({\rm AEFD}\) は円に内接する
したがって、4点 \({\rm A~,~E~,~F~,~D}\) は同一円周上にある [終]
4
[証明]
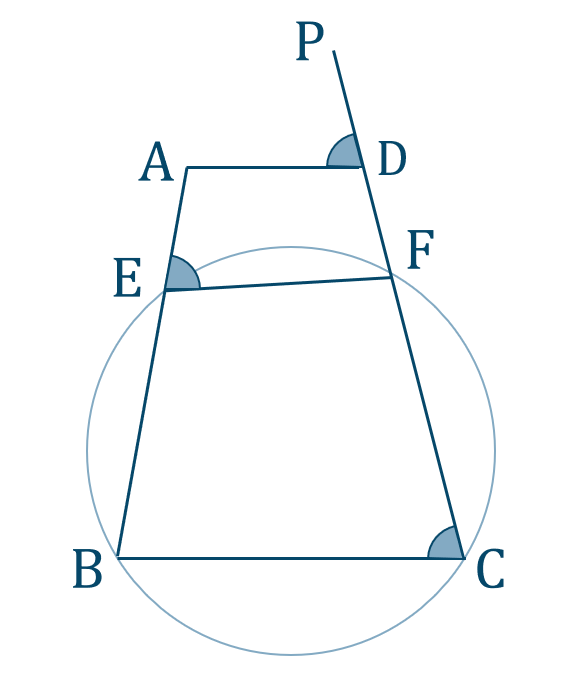
図のように、直線 \({\rm CD}\) の延長線上に点 \({\rm P}\) をとると、
\({\rm AD\parallel BC}\) の同位角より、
\(\angle{\rm ADP}=\angle{\rm BCF}\) …①
四角形 \({\rm EBCF}\) は円に内接しているので、外角の条件より、
\(\angle{\rm BCF}=\angle{\rm AEF}\) …②
①、②より、
\(\angle{\rm ADP}=\angle{\rm AEF}\)
四角形 \({\rm AEFD}\) において、1つの外角が隣り合う内角の対角に等しいので、四角形 \({\rm AEFD}\) は円に内接する
したがって、4点 \({\rm A~,~E~,~F~,~D}\) は同一円周上にある [終]
p.152
5
[証明]

図のように、四角形 \({\rm ABCD}\) と円との接点を \({\rm P~,~Q~,~R~,~S}\) とすると、
接線の条件より、
\({\rm AP=AS}=a\)
\({\rm BP=BQ}=b\)
\({\rm CQ=CR}=c\)
\({\rm DR=DS}=d\)
よって、
\({\rm AB+CD}\)
\({\rm =AP+BP+CR+DR}\)
\(=a+b+c+d\)
また、
\({\rm AD+BC}\)
\({\rm =AS+DS+BQ+CQ}\)
\(=a+d+b+c\)
\(=a+b+c+d\)
したがって、
\({\rm AB+CD=AD+BC}\) [終]
5
[証明]
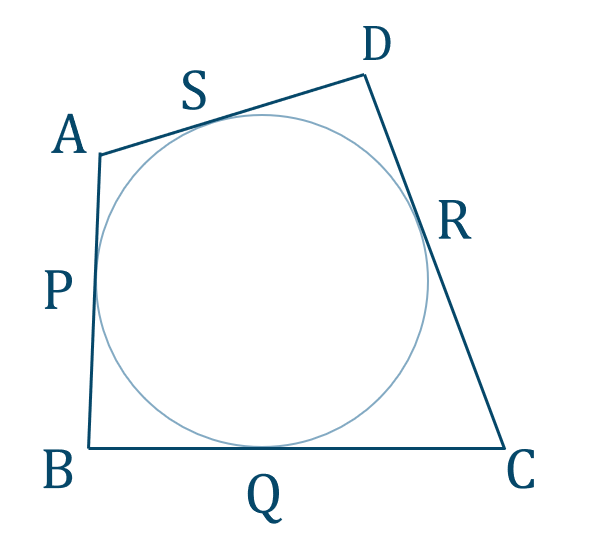
図のように、四角形 \({\rm ABCD}\) と円との接点を \({\rm P~,~Q~,~R~,~S}\) とすると、
接線の条件より、
\({\rm AP=AS}=a\)
\({\rm BP=BQ}=b\)
\({\rm CQ=CR}=c\)
\({\rm DR=DS}=d\)
よって、
\({\rm AB+CD}\)
\({\rm =AP+BP+CR+DR}\)
\(=a+b+c+d\)
また、
\({\rm AD+BC}\)
\({\rm =AS+DS+BQ+CQ}\)
\(=a+d+b+c\)
\(=a+b+c+d\)
したがって、
\({\rm AB+CD=AD+BC}\) [終]
p.153
6
[証明] 円 \({\rm O}\) について、方べきの定理より、
\({\rm PQ^2=PA\cdot PB}\) …①
円 \({\rm O’}\) について、方べきの定理より、
\({\rm PR^2=PA\cdot PB}\) …②
①、②より、
\({\rm PQ^2=PR^2}\)
辺の長さより \({\rm PQ>0~,~PR>0}\) であるので、
\({\rm PQ=PR}\) [終]
6
[証明] 円 \({\rm O}\) について、方べきの定理より、
\({\rm PQ^2=PA\cdot PB}\) …①
円 \({\rm O’}\) について、方べきの定理より、
\({\rm PR^2=PA\cdot PB}\) …②
①、②より、
\({\rm PQ^2=PR^2}\)
辺の長さより \({\rm PQ>0~,~PR>0}\) であるので、
\({\rm PQ=PR}\) [終]
p.153
7
\({\small (1)}~\)[証明] \(\triangle {\rm OCH}\) と \(\triangle {\rm ODH}\) において、
\(\angle{\rm OHC}=\angle{\rm OHD}=90^\circ\)
円の半径より、
\({\rm OC=OD}\)
共通な辺より、
\({\rm OH=OH}\)
斜辺と他の1組の辺がそれぞれ等しいので、
\(\triangle {\rm OCH}\equiv\triangle {\rm ODH}\)
よって、
\({\rm CH=DH}\)
ここで、\({\rm AB~,~CD}\) について方べきの定理より、
\({\rm CH\cdot DH=AH\cdot BH}\)
\({\rm DH=CH~,~AH=}a~,~{\rm BH=}b\) より、
\({\rm CH^2}=ab\)
\({\rm CH}>0\) であるので、
\({\rm CH}=\sqrt{ab}\) [終]
\({\small (2)}~\)

7
\({\small (1)}~\)[証明] \(\triangle {\rm OCH}\) と \(\triangle {\rm ODH}\) において、
\(\angle{\rm OHC}=\angle{\rm OHD}=90^\circ\)
円の半径より、
\({\rm OC=OD}\)
共通な辺より、
\({\rm OH=OH}\)
斜辺と他の1組の辺がそれぞれ等しいので、
\(\triangle {\rm OCH}\equiv\triangle {\rm ODH}\)
よって、
\({\rm CH=DH}\)
ここで、\({\rm AB~,~CD}\) について方べきの定理より、
\({\rm CH\cdot DH=AH\cdot BH}\)
\({\rm DH=CH~,~AH=}a~,~{\rm BH=}b\) より、
\({\rm CH^2}=ab\)
\({\rm CH}>0\) であるので、
\({\rm CH}=\sqrt{ab}\) [終]
\({\small (2)}~\)
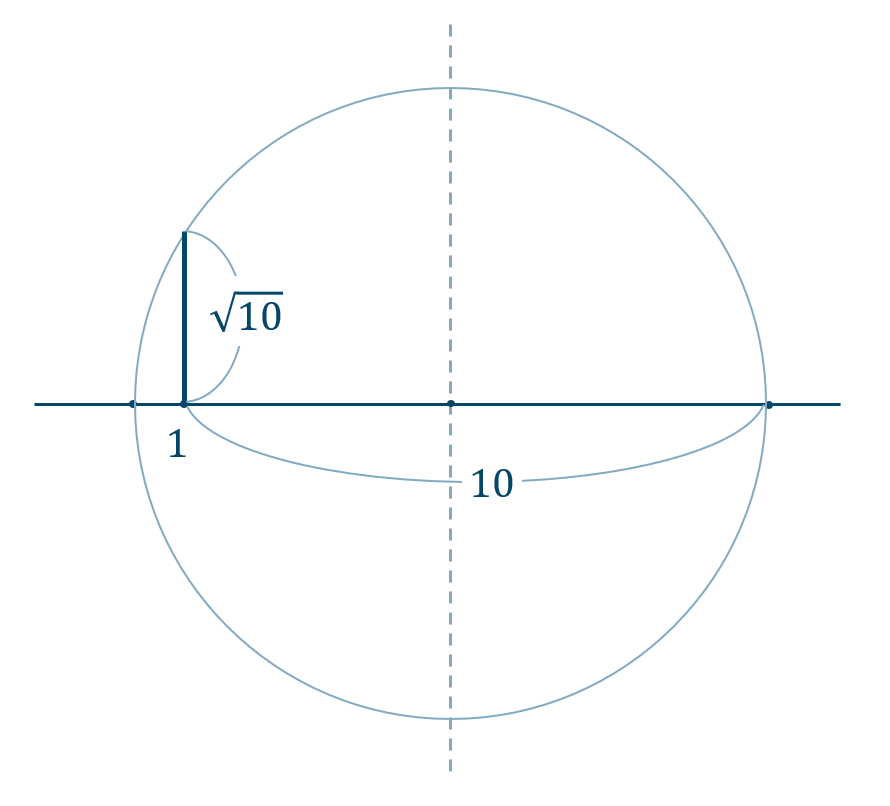
p.153
8
\(60^\circ\)
8
\(60^\circ\)
p.153
9
\({\small (1)}~\sqrt{2}a\) \({\small (2)}~{\large \frac{\sqrt{2}}{3}}a^3\)
\({\small (3)}~2\sqrt{3}a^2\)
9
\({\small (1)}~\sqrt{2}a\) \({\small (2)}~{\large \frac{\sqrt{2}}{3}}a^3\)
\({\small (3)}~2\sqrt{3}a^2\)
次のページ「資料 集合」