p.104 問8[証明] 接弦定理より、
　$\angle{\rm ACB}=\angle{\rm BAD}$
また、${\rm AC=AD}$ より $\triangle {\rm ACD}$ は二等辺三角形となり底角が等しいので、
　$\angle{\rm ACD}=\angle{\rm ADC}$
よって、
　$\angle{\rm BAD}=\angle{\rm BDA}$
底角が等しいので、$\triangle {\rm BAD}$ は二等辺三角形となる
したがって、
　${\rm BA=BD}$ [終]

p.104 問9[証明] 円周角の定理より、
　$\angle{\rm BAD}=\angle{\rm BCD}$
また、接線と弦のつくる角の定理より、
　$\angle{\rm CDT}=\angle{\rm DAC}$
仮定より $\angle{\rm BAD}=\angle{\rm DAC}$ であるので、
　$\angle{\rm BAD}=\angle{\rm CDT}$
錯覚が等しいので、
　${\rm BC\,//\, DT}$ [終]

p.106 問10$${\small (1)}~9$$$${\small (2)}~5$$→ 方べきの定理

p.107 問11$${\small (1)}~3\sqrt{5}$$$${\small (2)}~{ \frac{\,5\,}{\,2\,}}$$→ 方べきの定理

p.109 問12${\small (1)}~$４本
${\small (2)}~$３本
${\small (3)}~$２本
${\small (4)}~$１本
${\small (5)}~$０本
→ ２つの円の位置関係と共通接線

p.109 問13$${\small (1)}~5\sqrt{3}$$$${\small (2)}~12$$→ 共通接線の長さ

Training

p.113 Training 7$${\small (1)}~47^\circ$$$${\small (2)}~40^\circ$$$${\small (3)}~83^\circ$$

p.113 Training 8$${\small (1)}~{ \frac{\,21\,}{\,2\,}}$$$${\small (2)}~4$$

p.113 Training 9$${\small (1)}~28^\circ$$$${\small (2)}~20^\circ$$

p.113 Training 10$${\small (1)}~{ \frac{\,5\,}{\,2\,}}$$$${\small (2)}~5$$

p.113 Training 11$$~~~2\sqrt{22}$$

p.113 Training 12$$\begin{split}&r-r’=2\\[2pt]~~~&r+r’=6\\[2pt]~~~&d=3\end{split}$$これより、$$~~~r-r'< d< r+r’$$したがって、２つの円は２点で交わる

３節　空間図形

p.115 問1$${\small (1)}~90^\circ$$$${\small (2)}~45^\circ$$$${\small (3)}~60^\circ$$

p.117 問2$${\small (1)}~45^\circ$$$${\small (2)}~90^\circ$$→ 空間図形の位置関係

p.119 問3[証明] $\triangle {\rm OAB}$ において、
${\rm OA=OC}$ の二等辺三角形で、点 ${\rm P}$ は正方形 ${\rm ABCD}$ の対角線の交点より
　${\rm AP=CP}$
よって、
　${\rm OP\perp AC}$
$\triangle {\rm OBD}$ でも同様に考えて、
　${\rm OP\perp BD}$
したがって、直線 ${\rm OP}$ は面 ${\rm ABCD}$ 上の２直線 ${\rm AC~,~BD}$ に垂直であるので、
　平面 ${\rm ABCD\perp OP}$ [終]

p.120 問4${\small (1)}~$[証明] 直線 $l$ は $\alpha$ 上にあるので、${\rm PO}\perp\alpha$ より、
　${\rm PO}\perp l$
また、仮定より
　${\rm OA}\perp l$
ここで、平面 ${\rm PAO}$ 上の２直線に垂直であるので、
　$l\perp$ 平面 ${\rm PAO}$
したがって、平面 ${\rm PAO}$ 上の直線 ${\rm PA}$ に対しても ${\rm PA}\perp l$ [終]

${\small (2)}~$[証明] 直線 $l$ は平面 $\alpha$ 上にあり、
　${\rm PO}\perp \alpha$ より ${\rm PO}\perp l$
また、仮定より ${\rm PA}\perp l$
よって、平面 ${\rm PAO}$ 上の２直線に垂直であるので、
　$l\perp $ 平面 ${\rm PAO}$
したがって、平面 ${\rm PAO}$ 上の直線 ${\rm OA}$ に対しても ${\rm OA}\perp l$ [終]

Training

p.121 Training 13[証明] $\triangle {\rm ABD}$ において、
${\rm AP:AB=AS:AD}=2:3$ であり、平行線と線分の比の関係より、
　${\rm PS\,//\, BD}$
　${\rm PS:BD}=2:3$
次に、$\triangle {\rm CBD}$ において、
${\rm CQ:CB=CR:CD}=2:3$ であり、平行線と線分の比の関係より、
　${\rm QR\,//\, BD}$
　${\rm QR:BD}=2:3$
これらより、
　${\rm PS\,//\, QR}$
　${\rm PS=QR}$
１組の対辺が平行で等しいので、四角形 ${\rm PQRS}$ は平行四辺形である [終]

p.121 Training 14$${\small (1)}~45^\circ$$$${\small (2)}~90^\circ$$

p.121 Training 15$${\small (1)}~45^\circ$$$${\small (2)}~30^\circ$$$${\small (3)}~90^\circ$$

p.121 Training 16${\small (1)}~$[証明] 正方形 ${\rm ABCD}$ の対角線は直交するので、
　${\rm AC\perp BD}$　…①
${\rm AE\,//\, BF}$ で四角形 ${\rm BFHD}$ が長方形より、${\rm BD}$ と ${\rm BF}$ のなす角が $90^\circ$となり、 ${\rm BD}$ と ${\rm AE}$ のなす角が $90^\circ$ となるので、
　${\rm AE\perp BD}$　…②
よって、${\rm AC~,~AE}$ は平面 ${\rm AECG}$ 上の直線であり、①と②より直線 ${\rm BD}$ はこの２直線にそれぞれ直交する
したがって
直線 ${\rm BD}$ $\perp$ 平面 ${\rm AEGC}$ [終]

${\small (2)}~$[証明] (1) より、平面 ${\rm AEGC}$ 上のすべての直線が直線 ${\rm BD}$ と垂直であるので、
　${\rm CE\perp BD}$ [終]

p.121 Training 17[証明] ${\rm \triangle {\rm ACD}}$ は正三角形であり、点 ${\rm M}$ は線分 ${\rm CD}$ の中点であるので、
　${\rm AM\perp CD}$
次に、${\rm \triangle {\rm BCD}}$ は正三角形であり、点 ${\rm M}$ は線分 ${\rm CD}$ の中点であるので、
　${\rm BM\perp CD}$
仮定より
　${\rm AH\perp BM}$
したがって、三垂線の定理より
　${\rm AH} \perp$ 平面 ${\rm BCD}$ [終]

p.121 Training 18$\alpha$ 上の直線 $g$ が $l$ と交わり、$m$ と垂直であるとき

Level Up　図形の性質

p.122 Level Up 1$${\small (1)}~{ \frac{\,7\,}{\,2\,}}$$$${\small (2)}~2:1$$

p.122 Level Up 2[証明]

平行四辺形の対角線の交点を ${\rm O}$ とする
　${\rm AO=CO~,~BO=DO}$
これより、点 ${\rm P}$ は $\triangle {\rm ABC}$ の重心となり、
　${\rm BP:PO}=2:1$
また、点 ${\rm Q}$ は $\triangle {\rm AC}$ の重心となり、
　${\rm DQ:QO}=2:1$
${\rm BO:DO}=1:1$ より、$$\begin{eqnarray}~~~{\rm BP}&=&\frac{\,1\,}{\,2\,}\times\frac{\,2\,}{\,3\,}{\rm BD}=\frac{\,1\,}{\,3\,}{\rm BD}\\[3pt]~~~{\rm QD}&=&\frac{\,1\,}{\,2\,}\times\frac{\,2\,}{\,3\,}{\rm BD}=\frac{\,1\,}{\,3\,}{\rm BD}\\[3pt]~~~{\rm PQ}&=&{\rm PO+QO}\\[3pt]~~~&=&\frac{\,1\,}{\,2\,}\times\frac{\,1\,}{\,3\,}{\rm BD}+\frac{\,1\,}{\,2\,}\times\frac{\,1\,}{\,3\,}{\rm BD}\\[3pt]~~~&=&\frac{\,1\,}{\,3\,}{\rm BD}\end{eqnarray}$$したがって、$$~~~{\rm BP=PQ=QD}$$[終]

p.122 Level Up 3$$~~~3:8$$

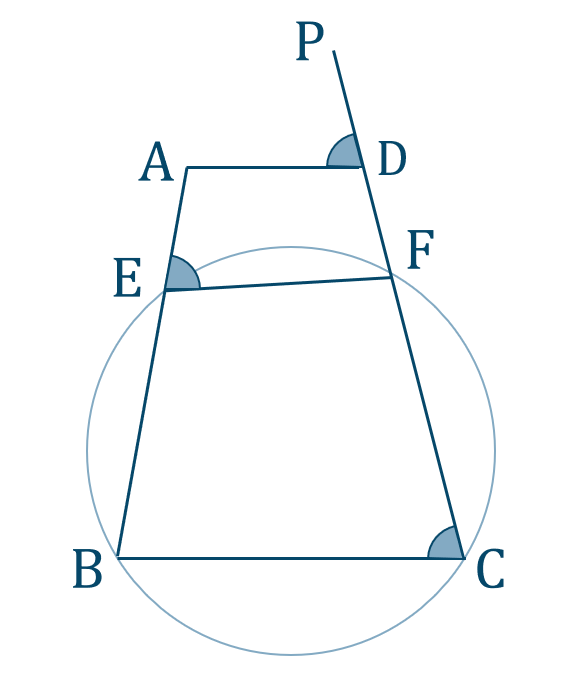
p.122 Level Up 4[証明]

図のように、直線 ${\rm CD}$ の延長線上に点 ${\rm P}$ をとると、
${\rm AD\,//\, BC}$ の同位角より、
　$\angle{\rm ADP}=\angle{\rm BCF}$　…①
四角形 ${\rm EBCF}$ は円に内接しているので、外角の条件より、
　$\angle{\rm BCF}=\angle{\rm AEF}$　…②
①、②より、
　$\angle{\rm ADP}=\angle{\rm AEF}$
四角形 ${\rm AEFD}$ において、１つの外角が隣り合う内角の対角に等しいので、四角形 ${\rm AEFD}$ は円に内接する
したがって、４点 ${\rm A~,~E~,~F~,~D}$ は同一円周上にある [終]

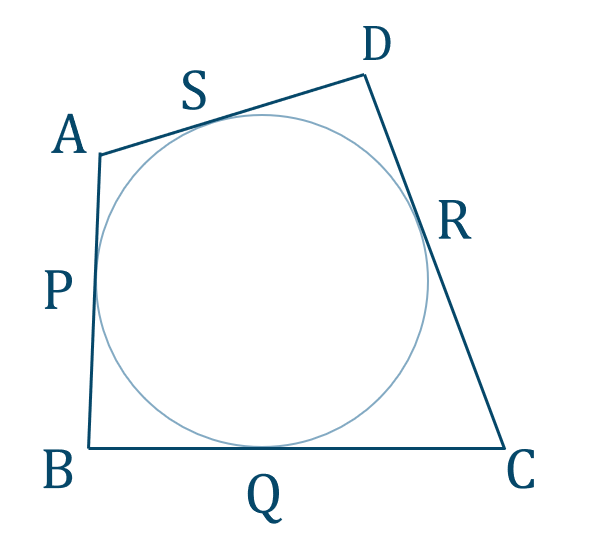
p.123 Level Up 5[証明]

図のように、四角形 ${\rm ABCD}$ と円との接点を ${\rm P~,~Q~,~R~,~S}$ とすると、
接線の条件より、
　${\rm AP=AS}=a$
　${\rm BP=BQ}=b$
　${\rm CQ=CR}=c$
　${\rm DR=DS}=d$
よって、
　${\rm AB+CD}$
${\rm =AP+BP+CR+DR}$
$=a+b+c+d$
また、
　${\rm AD+BC}$
${\rm =AS+DS+BQ+CQ}$
$=a+d+b+c$
$=a+b+c+d$
したがって、
　${\rm AB+CD=AD+BC}$ [終]

p.123 Level Up 6[証明] 円 ${\rm O}$ について、方べきの定理より、
　${\rm PQ^2=PA\cdot PB}$　…①
円 ${\rm O’}$ について、方べきの定理より、
　${\rm PR^2=PA\cdot PB}$　…②
①、②より、
　${\rm PQ^2=PR^2}$
辺の長さより ${\rm PQ>0~,~PR>0}$ であるので、
　${\rm PQ=PR}$ [終]

p.123 Level Up 7$$~~~60^\circ$$

p.123 Level Up 8$${\small (1)}~\sqrt{2}a$$$${\small (2)}~{ \frac{\,\sqrt{2}\,}{\,3\,}}a^3$$$${\small (3)}~2\sqrt{3}a^2$$

２章 図形の性質

１節 三角形と比

２節 円の性質

３節 空間図形

Level Up 図形の性質

２章　図形の性質

１節　三角形と比

２節　円の性質

３節　空間図形

Level Up　図形の性質