【新課程】数研出版：数学Ⅰ[712]

p.177 練習1

階級(℃) 以上 ~ 未満	度数
\(3\) ~ \(6\)	\(1\)
\(6\) ~ \(9\)	\(9\)
\(9\) ~ \(12\)	\(3\)
\(12\) ~ \(15\)	\(8\)
\(15\) ~ \(18\)	\(3\)
\(18\) ~ \(21\)	\(3\)
\(21\) ~ \(24\)	\(1\)
\(24\) ~ \(27\)	\(2\)
計	\(30\)

p.177 練習2
→ 度数分布表

p.178 練習3$$~~~15.1$$

p.179 練習4\(7\) 人の中央値 \(43\)
\(8\) 人の中央値 \(42\)

p.179 練習5$$~~~22.5$$→ 平均値・中央値・最頻値

p.181 練習6Ａ町 \(15\) 日、Ｂ町 \(5\) 日
Ａ町の方が散らばりの度合いが大きい

p.182 練習7\({\small (1)}~\)
　第１四分位数 \(65\)
　第３四分位数 \(77\)
\({\small (2)}~\)
　第１四分位数 \(22\)
　第３四分位数 \(31\)

p.183 練習8\({\small (1)}~2\)
\({\small (2)}~\)
Ａが一番散らばりの度合いが大きい
ＢとＣの散らばりの度合いはほぼ同じ

p.185 練習9
東京がデータの散らばり度合いが一番と大きい
大阪の四分位範囲は大きい方に分布
名古屋の四分位範囲は小さい方に分布
→ 箱ひげ図

p.186 深める外れ値を含む場合と含まない場合では平均値が大きく異なる。
また、中央値や最頻値は外れ値を含んでも値の変化は少ない。

p.188 練習10　分散 \(4\)、標準偏差 \(2\)

p.188 深める外れ値を含むと平均値に影響して、分散の値に影響を受ける。

p.189 問1　分散 \(1.4\)、標準偏差 \(1.2\)

p.189 練習11　分散 \(4.1\)、標準偏差 \(2.0\)
→ 分散と標準偏差

p.191 研究 練習1　平均値 \(59.0\)
　分散 \(29.16\)、標準偏差 \(5.4\)

p.192 研究 練習2\({\small (1)}~\)平均値 \({\large \frac{\,1\,}{\,2\,}}\) 、標準偏差 \({\large \frac{\,3\,}{\,2\,}}\)
\({\small (2)}~\)平均値 \(745\) 、標準偏差 \(15\)

p.194 練習12\({\small (1)}~\)

\({\small (2)}~\)負の相関がある
→ 散布図と相関

p.196 練習13$$~~~0.88$$

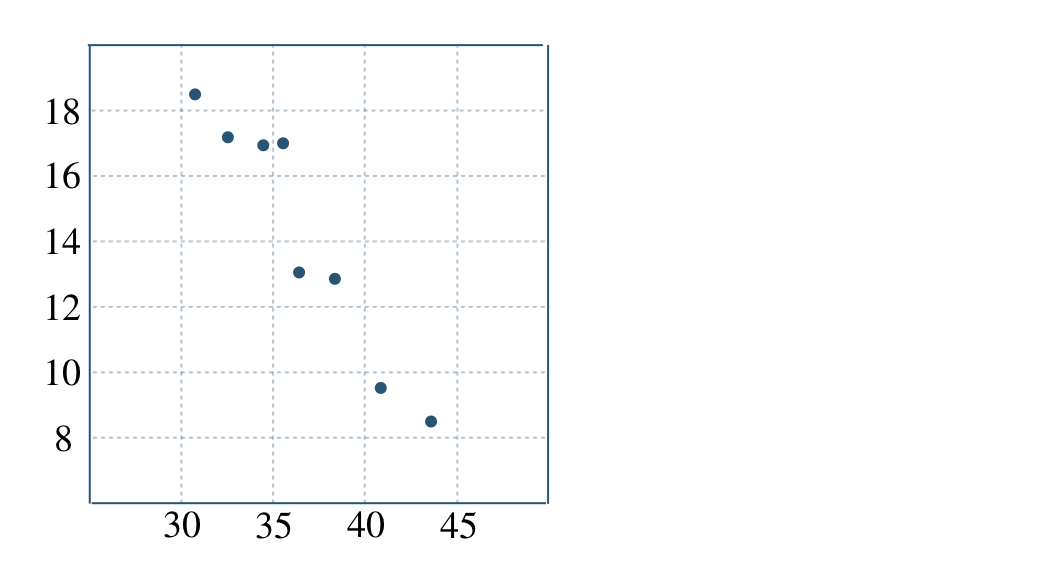
p.197 練習14$$~~~-0.71$$→ 相関係数

p.199 練習15\({\small (1)}~\)

\({\small (2)}~\)

p.199 深める教材Ｂの方が試験の合否に影響を及ぼしている

p.204 練習16水道水がおいしくなったと住民から評価されていると判断してよい。

p.205 発展 練習1このコインは表が出やすいと判断できない。