東京書籍：Advanced数学Ａ

p.6
問1
\({\small (1)}~\{2,4,6,8,10,12,14,16,18,20\}\)
\({\small (2)}~\{-3,3\}\)

p.7
問2
\({\rm A}\cup{\rm B}=\{1,2,3,4,5\}\)
\({\rm A}\cup{\rm C}=\{1,2,4,6\}\)
\({\rm B}\cap{\rm C}=\{4\}\)

p.7
問3
\({\small (1)}~\{1,3,5,7,8,9\}\)
\({\small (2)}~\{2,5,6,8,9\}\)
\({\small (3)}~\{5,8,9\}\)
\({\small (4)}~\{5,8,9\}\)

p.8
問1
\(4\)

p.9
問2
\(50\)
→ 集合の要素の個数

p.10
問3
\(67\)

p.11
問4
\({\small (1)}~150\)　\({\small (2)}~25\)
→ 補集合の要素の個数

p.12
問5
\(15\)

p.12
問6
\(18\)

p.13
問7
\(6\)

p.13
問8
\(4\)

p.14
問9
\(21\)

p.14
問10
\(6\)

p.15
問11
\(27\)
→ 和の法則と積の法則

p.15
問12
\({\small (1)}~12\)　\({\small (2)}~24\)
→ 約数の個数と展開式の項の個数

p.16
問13
\(60\)

p.17
問14
\({\small (1)}~20\)　\({\small (2)}~360\)　\({\small (3)}~210\)

p.17
問15
\(120~,~720\)
→ 順列と階乗の記号

p.18
問16
\(6840\)

p.18
問17
\(144\)

p.18
問18
\(36\)
→ 文字の順列

p.19
問19
\({\small (1)}~18\)　\({\small (2)}~30\)
→ 数字の順列

p.20
問20
\(24\)
→ 円順列とじゅず順列

p.21
問21
\({\small (1)}~48\)　\({\small (2)}~12\)
→ 条件付き円順列

p.21
問22
\({\small (1)}~125\)　\({\small (2)}~100\)
→ 重複を許す順列

p.23
問23
\({\small (1)}~10\)　\({\small (2)}~20\)　\({\small (3)}~210\)

p.23
問24
\(15\)

p.23
問25
\({\small (1)}~21\)　\({\small (2)}~8\)　\({\small (3)}~220\)
→ 組合せの記号

p.24
問26
\(20\)
→ 図形と組合せ

p.24
問27
\({\small (1)}~2100\)　\({\small (2)}~4795\)
→ 代表を選ぶ

p.25
問28
\({\small (1)}~70\)　\({\small (2)}~35\)
→ ３つのグループに分ける

p.26
問29
\(12600\)
→ 同じものを含む順列

p.27
問30
\({\small (1)}~126\)　\({\small (2)}~60\)　\({\small (3)}~66\)　\({\small (4)}~24\)
→ 最短経路問題

p.28
1
\({\small (1)}~720\)　\({\small (2)}~2880\)

p.28
2
\({\small (1)}~12\)　\({\small (2)}~24\)

p.28
3
\({\small (1)}~32\)　\({\small (2)}~30\)

p.28
4
[証明] \(n\) 個のもののなかから \(r\) 個取り出す組合せは、\({}_{n}{\rm C}_{r}\)
\(n\) 個のもののなかに特定の \(a\) があるとき、
(ⅰ) 取り出した \(r\) 個に特定の \(a\) を含む場合
\(a\) は取り出すのが確定しているので、それ以外の \(n-1\) 個のもののなかから \(r-1\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r-1}$$(ⅱ) 取り出した \(r\) 個に特定の \(a\) を含まない場合
\(a\) 以外の \(n-1\) 個のもののなかから \(r\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r}$$これらは同時に起こらないので和の法則より、$$~~~{}_{n}{\rm C}_{r}={}_{n-1}{\rm C}_{r-1}+{}_{n-1}{\rm C}_{r}$$[終]

p.28
5
\(60\)

p.28
6
\({\small (1)}~1260\)　\({\small (2)}~280\)　\({\small (3)}~378\)

p.28
7
\(120\)

p.29
参考1
\({\rm A}\cap({\rm B}\cup{\rm C})\) をベン図で表すと次のようになる

また、\({\rm A}\cap{\rm B}\) と \({\rm A}\cap{\rm C}\) をベン図で表すと次のようになる

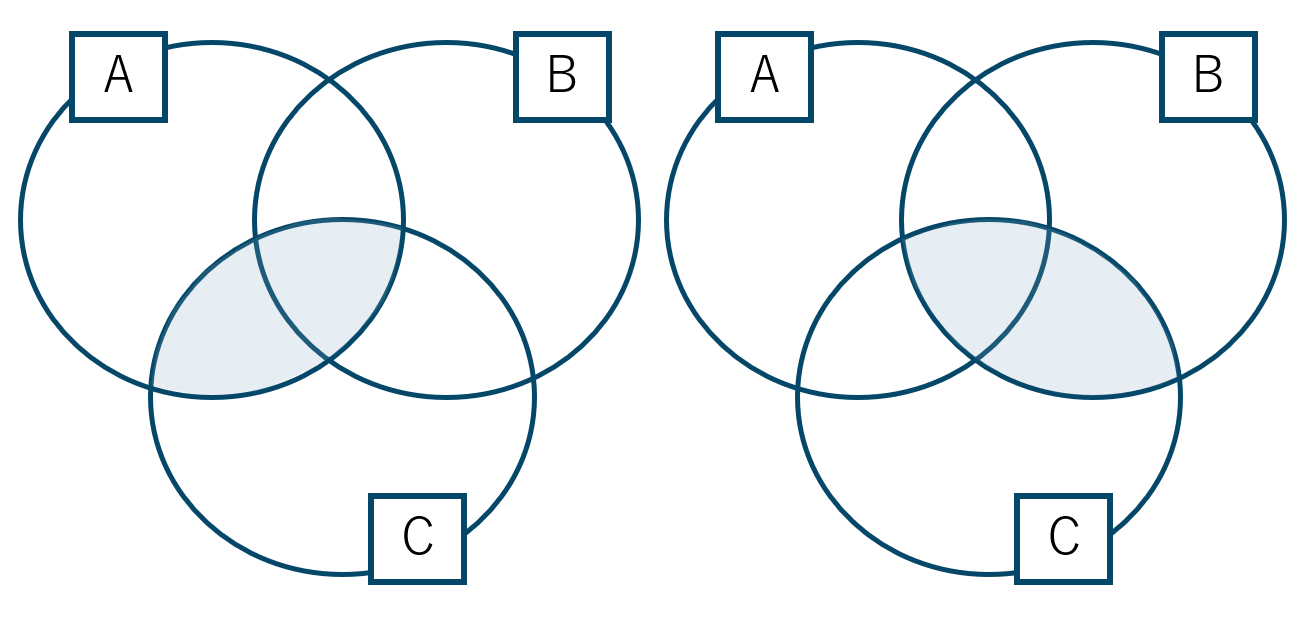
これらの和集合が上の \({\rm A}\cap({\rm B}\cup{\rm C})\) と一致する
したがって、
\({\rm A}\cap({\rm B}\cup{\rm C})=({\rm A}\cap{\rm B})\cup ({\rm A}\cap{\rm C})\)
→ ３つの集合の要素の個数

p.30
参考1
\(220\)

p.31
参考2
\(91\)
→ 等式を満たす自然数の組合せ

p.31
参考3
\(84\)
→ 重複組合せ

p.33
問1
\(\{1\}~,~\{3\}~,~\{5\}\)

p.33
問2
\({\rm U}=\{1,2,3,4,5,6,7,8,9,10\}\)
\({\rm A}=\{1,2,5,10\}\)

p.34
問3
\({\Large \frac{2}{3}}\)
→ 確率の基本

p.35
問4
\({\Large \frac{1}{9}}\)
→ さいころの確率

p.35
問5
\({\Large \frac{3}{10}}\)
→ ボールを取り出す確率

p.35
問6
\({\Large \frac{1}{15}}\)

p.35
問7
\({\small (1)}~{\Large \frac{1}{2}}\)　\({\small (2)}~{\Large \frac{1}{6}}\)
→ 一列に並べる確率

p.36
問8
\({\rm A}\cap{\rm B}=\{(2,2)\}\)
\({\rm A}\cup{\rm B}=\{(1,3),(1,4),(2,2),(3,1),(4,1)\}\)

p.37
問9
\({\rm A}\) と \({\rm B}\)、\({\rm A}\) と \({\rm C}\)

p.39
問10
\({\Large \frac{1}{6}}\)

p.40
問11
\({\Large \frac{6}{25}}\)
→ 和事象と排反事象

p.41
問12
\({\Large \frac{91}{216}}\)
→ 余事象の確率

p.42
8
\({\small (1)}~{\Large \frac{7}{24}}\)　\({\small (2)}~{\Large \frac{21}{40}}\)

p.42
9
\({\small (1)}~{\Large \frac{1}{10}}\)　\({\small (2)}~{\Large \frac{1}{2}}\)

p.42
10
\({\Large \frac{14}{45}}\)

p.42
11
\({\small (1)}~{\Large \frac{1}{10}}\)　\({\small (2)}~{\Large \frac{17}{50}}\)

p.42
12
\({\small (1)}~{\Large \frac{1}{9}}\)　\({\small (2)}~{\Large \frac{1}{3}}\)

p.42
13
\({\Large \frac{3}{4}}\)

p.42
14
\({\small (1)}~{\Large \frac{2}{7}}\)　\({\small (2)}~{\Large \frac{5}{7}}\)　\({\small (3)}~{\Large \frac{1}{2}}\)

p.43
問1
\({\small (1)}~\)独立である
\({\small (2)}~\)独立でない

p.45
問2
\({\Large \frac{1}{3}}\)

p.45
問3
\({\small (1)}~{\Large \frac{13}{25}}\)　\({\small (2)}~{\Large \frac{12}{25}}\)

p.45
問4
\({\small (1)}~{\Large \frac{57}{140}}\)　\({\small (2)}~{\Large \frac{32}{35}}\)
→ 独立試行の確率

p.47
問5
\({\Large \frac{10}{243}}\)

p.48
問6
\({\Large \frac{144}{625}}\)

p.48
問7
\({\Large \frac{13}{256}}\)

p.49
問8
\({\Large \frac{15}{64}}\)
→ 反復試行の確率①（コイン）
→ 反復試行の確率②（さいころ）

p.49
問9
\({\Large \frac{160}{729}}\)
→ 点が動く確率

p.50
問10
\({\small (1)}~{\Large \frac{81}{512}}\)　\({\small (2)}~{\Large \frac{459}{512}}\)
→ ○勝先取の確率

p.51
問11
\({\Large \frac{3}{19}}\)

p.52
問12
\({\Large \frac{2}{5}}\)
→ 条件付き確率

p.53
問13
\({\Large \frac{4}{15}}\)

p.53
問14
\({\Large \frac{1}{2}}\)
→ 確率の乗法定理

p.54
問15
\({\Large \frac{1}{9703}}\)

p.55
15
\({\small (1)}~{\Large \frac{9}{100}}\)　\({\small (2)}~{\Large \frac{99}{100}}\)

p.55
16
\({\Large \frac{1}{7}}\)

p.55
17
\({\small (1)}~{\Large \frac{8}{27}}\)　\({\small (2)}~{\Large \frac{16}{81}}\)　\({\small (3)}~{\Large \frac{64}{81}}\)

p.55
18
\({\Large \frac{3}{8}}\)

p.55
19
\({\Large \frac{3}{7}}\)

p.56
1
\(39\)

p.56
2
\(16\)

p.56
3
\({\small (1)}~480\)　\({\small (2)}~240\)

p.56
4
\({\Large \frac{13}{25}}\)

p.56
5
\({\small (1)}~{\Large \frac{1}{10}}\)　\({\small (2)}~{\Large \frac{33}{100}}\)

p.56
6
\({\Large \frac{3}{16}}\)

p.57
7
\(12\)

p.57
8
\({\small (1)}~1440\)　\({\small (2)}~840\)

p.57
9
\({\Large \frac{108}{343}}\)

p.57
10
\(3\) 個または \(6\) 個

p.57
11
\({\Large \frac{496}{729}}\)

p.57
12
\({\small (1)}~{\Large \frac{197}{5000}}\)　\({\small (2)}~{\Large \frac{297}{394}}\)