【新課程】数研出版：新編数学Ａ[714]

p.116 練習1\({\small (1)}~\)(例) \(100\)
\({\small (2)}~10\) の倍数となる

p.117 練習2$${\small (1)}~\pm1~,~\pm2~,~\pm3~,~\pm4~,~\pm6~,~\pm12$$$${\small (2)}~6~,~12~,~18~,~24~,~30$$→ 約数と倍数

p.118 練習3４桁の自然数 \(N\) の千の位を \(a\)、百の位を \(b\)、十の位を \(c\)、一の位を \(d\) とすると、$$\begin{eqnarray}~~~N&=&1000a+100b+10c+d\\[2pt]~~~&=&8\times125a+(100b+10c+d)\end{eqnarray}$$よって、\(N\) が \(8\) の倍数となるのは、
\(100b+10c+d\) が \(8\) の倍数であればよい
したがって、下３桁が \(8\) の倍数のときである

p.119 練習4$$~~~5$$→ 倍数判別法

p.120 練習5$$~~~2~,~3~,~5~,~7~,~11~,~13~,~17$$$$~~~,~19~,~23~,~29~,~31~,~37~,~41$$$$~~~,~43~,~47~,~53~,~59~,~61~,~67$$$$~~~,~71~,~73~,~79~,~83~,~89~,~97$$

p.120 深める２行目以降では、\(7\) で割った余りが \(1\) または \(5\) となる列に何度も現れる

p.121 練習6$${\small (1)}~2^4\cdot3^2$$$${\small (2)}~2^2\cdot3^2\cdot5$$$${\small (3)}~3\cdot5^2\cdot7$$→ 素因数分解

p.122 練習7$${\small (1)}~1~,~2~,~4~,~7~,~8~,~14~,~28~,~56$$$${\small (2)}~1~,~2~,~3~,~5~,~6~,~9~,~10$$$$~~~~~15~,~18~,~30~,~45~,~90$$

p.123 練習8\({\small (1)}~6\) 個
\({\small (2)}~9\) 個
\({\small (3)}~18\) 個
→ 約数の個数・平方数

p.123 練習9\({\small (1)}~\)奇数
\({\small (2)}~\)奇数
\({\small (3)}~\)(1) と (2) より、正の約数の個数が奇数であれば、ひっくり返された回数が奇数となり、裏向きのカードとなる
\(1\) 〜 \(15\) までの数を素因数分解し、正の約数の個数を調べると、
　\(1=1^1\) 正の約数 \(1\) 個
　\(2=2^1\) 正の約数 \(2\) 個
　\(3=3^1\) 正の約数 \(2\) 個
　\(4=2^2\) 正の約数 \(3\) 個
　\(5=5^1\) 正の約数 \(2\) 個
　\(6=2^1\cdot 3^1\) 正の約数 \(4\) 個
　\(7=7^1\) 正の約数 \(2\) 個
　\(8=2^3\) 正の約数 \(4\) 個
　\(9=3^2\) 正の約数 \(3\) 個
　\(10=2^1\cdot 5^1\) 正の約数 \(4\) 個
　\(11=11^1\) 正の約数 \(2\) 個
　\(12=2^2\cdot 3^1\) 正の約数 \(6\) 個
　\(13=13^1\) 正の約数 \(2\) 個
　\(14=2^1\cdot 7^1\) 正の約数 \(4\) 個
　\(15=3^1\cdot 5^1\) 正の約数 \(4\) 個
これより、正の約数の個数が奇数となるのは、
　\(1=1^2~,~4=2^2~,~9=3^2\)
これらで、\(n^2\) の形をした数だけである

p.124 練習10$${\small (1)}~1~,~2~,~3~,~4~,~5~,~6~,~10$$$$~~~~~12~,~15~,~20~,~30~,~60$$$${\small (2)}~1~,~2~,~3~,~6~,~8~,~9~,~12$$$$~~~~~18~,~24~,~36~,~72$$$${\small (3)}~a=12$$

p.125 練習11$${\small (1)}~12$$$${\small (2)}~35$$$${\small (3)}~4$$→ 最大公約数と最小公倍数

p.125 練習12$$~~~a=24$$

p.127 練習13$${\small (1)}~360$$$${\small (2)}~4200$$$${\small (3)}~1260$$→ 最大公約数と最小公倍数

p.127 練習14　\(465\) 年後

p.128 練習15$${\small (1)}~4~~~11~~~18~~~25~~~32$$$$~~~~~39~~~46~~~53~~~60~~~67$$$$~~~~~74~~~81~~~88~~~95~~~102$$$${\small (2)}~4~~~1~~~3~~~0~~~2$$$$~~~~~4~~~1~~~3~~~0~~~2$$$$~~~~~4~~~1~~~3~~~0~~~2$$$${\small (3)}~53$$

p.129 練習16\({\small (1)}~\)商 \(4\)、余り \(4\)
\({\small (2)}~\)商 \(-7\)、余り \(1\)

p.130 練習17$${\small (1)}~2$$$${\small (2)}~3$$$${\small (3)}~2$$$${\small (4)}~0$$→ 除法の性質

p.131 練習18[証明]
\(70a+21b+15c\) を \(3\) で割った余りは、$$~~~70a+21b+15c=3(23a+7b+5c)+a$$これより、\(a\) となる
 
\(70a+21b+15c\) を \(5\) で割った余りは、$$~~~70a+21b+15c=5(14a+4b+3c)+b$$これより、\(b\) となる
 
\(70a+21b+15c\) を \(7\) で割った余りは、$$~~~70a+21b+15c=7(10a+3b+2c)+c$$これより、\(c\) となる
[終]

p.131 練習19$$~~~71$$

p.132 練習20それぞれを素因数分解すると、
　\(391=17\times23~,~299=13\times23\)
よって、\(391\) と \(299\) の最大公約数である

p.133 練習21$${\small (1)}~37$$$${\small (2)}~29$$$${\small (3)}~19$$→ ユークリッドの互除法

p.134 練習22$$~~~\frac{\,1\,}{\,13\,}$$

p.134 練習23$$~~~\frac{\,3\,}{\,10\,}$$

p.135 練習24長方形 \({\rm IFHC}\)
[証明]$$\begin{eqnarray}~~~{\rm IF}&=&\sqrt{2}-1\\[2pt]~~~{\rm IC}&=&1-(\sqrt{2}-1)=2-\sqrt{2}\end{eqnarray}$$ここで、$$\begin{split}&{\rm IF:IC}\\[2pt]~~=~&\sqrt{2}-1:2-\sqrt{2}\\[3pt]~~=~&\frac{\,\sqrt{2}-1\,}{\,\sqrt{2}-1\,}:\frac{\,2-\sqrt{2}\,}{\,\sqrt{2}-1\,}\\[3pt]~~=~&1:\sqrt{2}\end{split}$$よって、$$~~~{\rm IF:IC=AD:AB}$$したがって、もとの長方形と相似である
[終]

p.136 練習25(例)

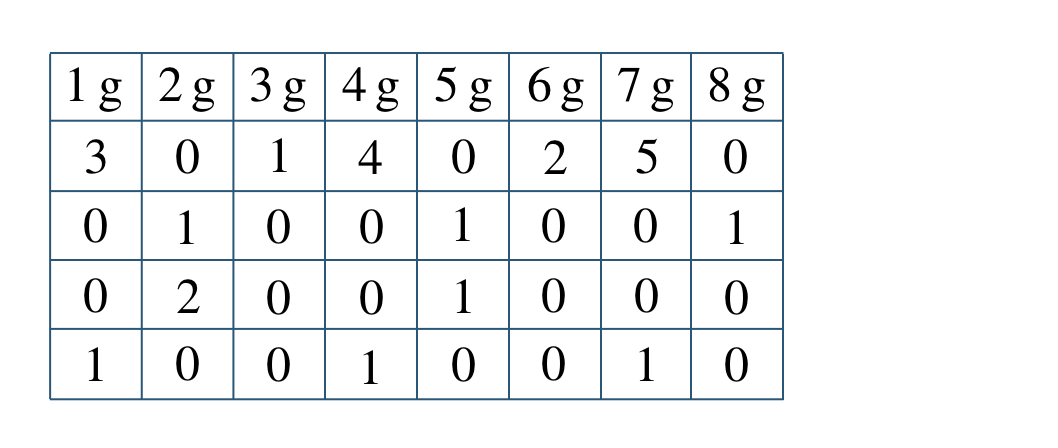
p.138 練習26$${\small (1)}~x=-2~,~y=5$$$${\small (2)}~x=9~,~y=-21$$

p.139 練習27\(k\) を整数とする$${\small (1)}~x=7k+2~,~y=-4k-1$$$${\small (2)}~x=7k+2~,~y=5k+1$$$${\small (3)}~x=22k-7~,~y=-31k+10$$→ 不定方程式①

p.139 練習28\({\small (1)}~\)\(k\) を整数とする
　\(x=3k+2~,~y=7k+3\)
\({\small (2)}~\)\(x\) が正で最も小さくなるときの \(k\) の値は、\(k=0\)
よって、このときの \(x~,~y\) の値は、$$\begin{eqnarray}~~~x&=&3\times0+2=2\\[2pt]~~~y&=&7\times0+3=3\end{eqnarray}$$したがって、\(x=2~,~y=3\) となる
\({\small (3)}~\)
　①→②→③→②→③→①→②→③
→ 不定方程式②（互除法）

p.140 練習29\({\small (1)}~\)

\({\small (2)}~\)

p.141 練習30$${\small (1)}~{\rm LXXXVII}$$$${\small (2)}~{\rm DCXXIX}$$

p.141 深める位が上がっても新しい数字(記号)が現れない

p.142 練習31$${\small (1)}~36$$$${\small (2)}~59$$$${\small (3)}~236$$$${\small (4)}~55$$→ n進法①（10進法で表す）

p.143 練習32$${\small (1)}~101101_{(2)}$$$${\small (2)}~110111_{(2)}$$$${\small (3)}~10201_{(3)}$$→ n進法②（n進法で表す）

p.145 練習33$${\small (1)}~(4~,~3)$$$${\small (2)}~(-1~,~-5)$$

p.145 練習34点 \({\rm O}\) から東へ \(12~{\rm m}\)、北へ \(9~{\rm m}\) 進んだ位置

p.145 深める点 \({\rm O}\) を中心に半径 \(13\) の円と、点 \({\rm A}\) を中心に半径 \(37\) の円をかき、これら２つの円の交点のうち北側( \(y>0\) )の点が \({\rm P}\) となる

p.147 練習35$${\small (1)}~(3~,~6~,~2)$$$${\small (2)}~(-4~,~4~,~-3)$$

p.147 練習36[証明]$$\begin{eqnarray}~~~{\rm OQ^2}&=&{\rm OA^2+AQ^2}\\[2pt]~~~&=&{\rm OA^2+OB^2}\\[2pt]~~~&=&a^2+b^2\end{eqnarray}$$また、\({\rm PQ^2=OC^2}=c^2\)
よって、\({\rm OP^2=OQ^2+PQ^2}\) より、$$\begin{eqnarray}~~~{\rm OP^2}&=&(a^2+b^2)+c^2\\[2pt]~~~&=&a^2+b^2+c^2\end{eqnarray}$$[終]

p.148 練習37先手が書いた◯の上下左右の4ヶ所のいずれかに書いたとき

p.149 練習38先手が中央に◯を置いたとき、
(ⅰ) 後手が先手の置いた◯の上下左右の4ヶ所のいずれかに置いたとき、

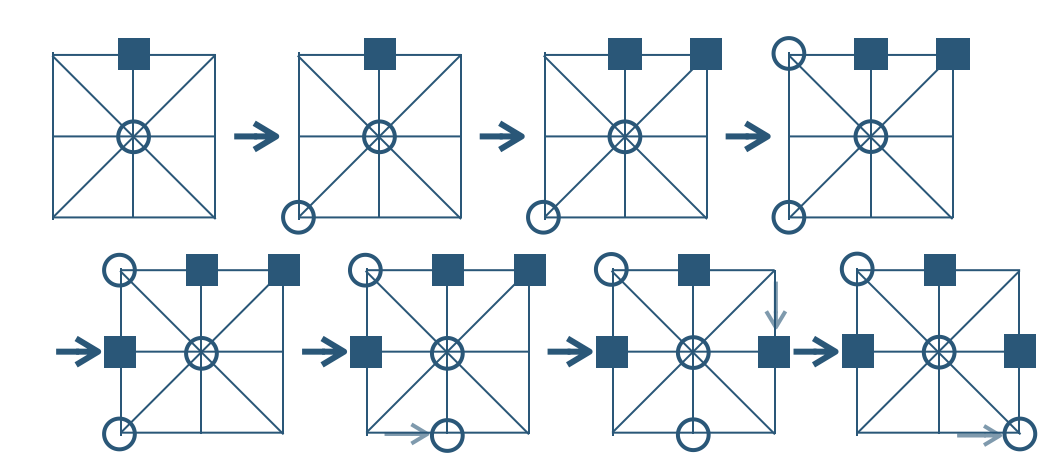
(ⅱ) 後手が四隅の4ヶ所のいずれかに置いたとき、

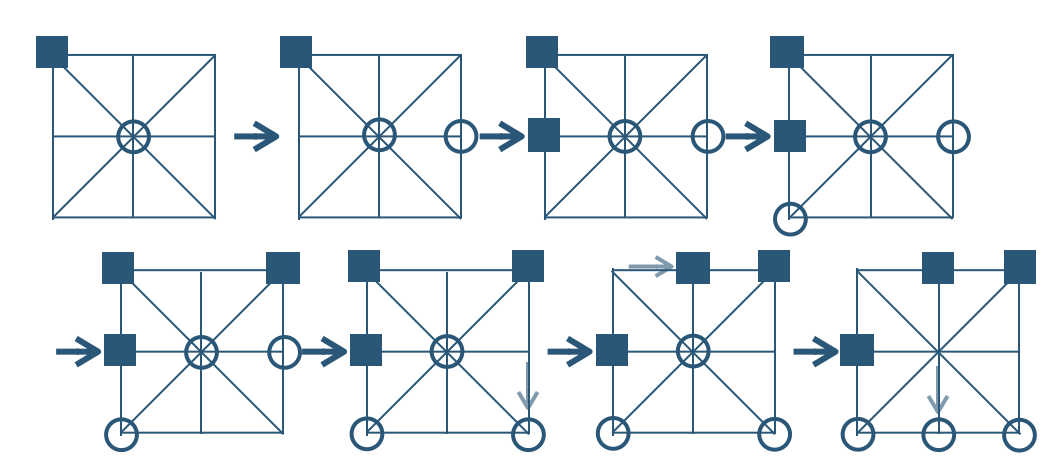
これより、先手が必ず勝つ方法はあるが、後手が必ず勝つ方法はない

p.150 練習39\({\small (1)}~~(1~,~5~,~9)~,~(1~,~6~,~8)\)
\({\small (2)}~\)\(1\) を含む \(3\) 個の数の和が \(15\) となるのは \(2\) 組しかない
四隅の \(4\) マスでは \(3\) 組必要になるので \(1\) は入らない

p.151 練習40\({\small (1)}~\)

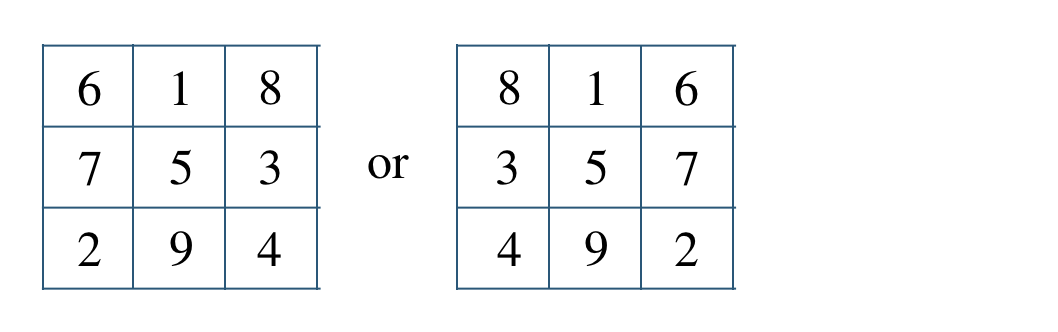
\({\small (2)}~\)

p.151 練習41$${\large ①}~~1+4+13+16=34$$$${\large ②}~~7+6+11+10=34$$$${\large ③}~~1+14+12+7=34$$$$~~~~~~15+4+6+9=34$$$$~~~~~~8+11+13+2=34$$$$~~~~~~10+5+3+16=34$$

p.152 練習42例17より、$$\begin{eqnarray}~~~{\rm 4S-N}&=&{\rm 4S-M}\\[2pt]~~~{\rm N}&=&{\rm M}\end{eqnarray}$$また、\({\rm M+N=2S}\) となるので、$$\begin{eqnarray}~~~\rm M+N&=&2S\\[2pt]~~~\rm M+M&=&2S\\[2pt]~~~\rm M&=& S=34\end{eqnarray}$$また、\({\rm N=M}\) より、$$~~~{\rm N=S}=34$$したがって、①と②の４つの数の和が魔法陣で \(34\) となる

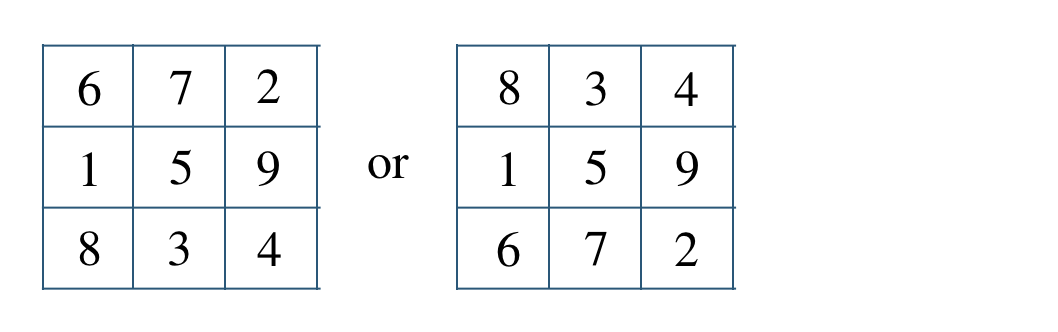
p.153 練習43$${\small (1)}~a=1~,~b=8~,~c=14$$

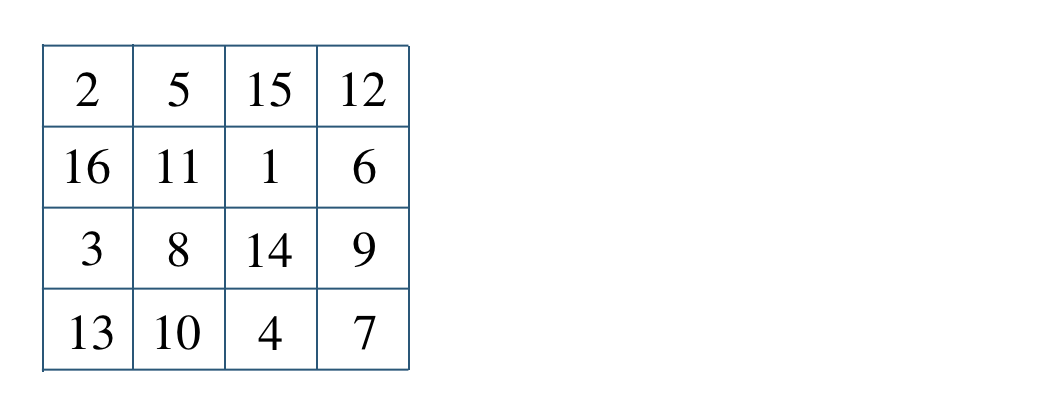
$${\small (2)}~a=15~,~b=2~,~c=8$$

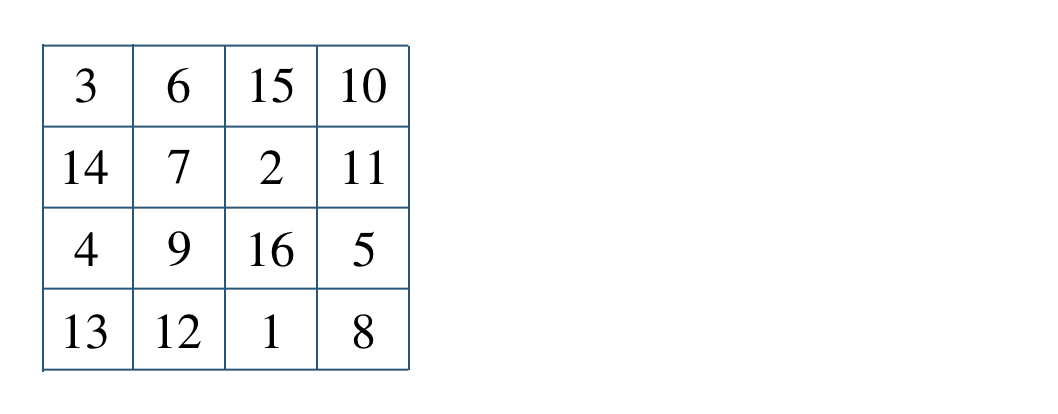
p.153 練習44\({\rm S}=34\) として、左上の４つの数の和を \({\rm A}\)、右下の４つの数の和を \({\rm B}\) とする
また、全体から右下の４つの数の和を除いた部分の和を \({\rm T}\) とすると、

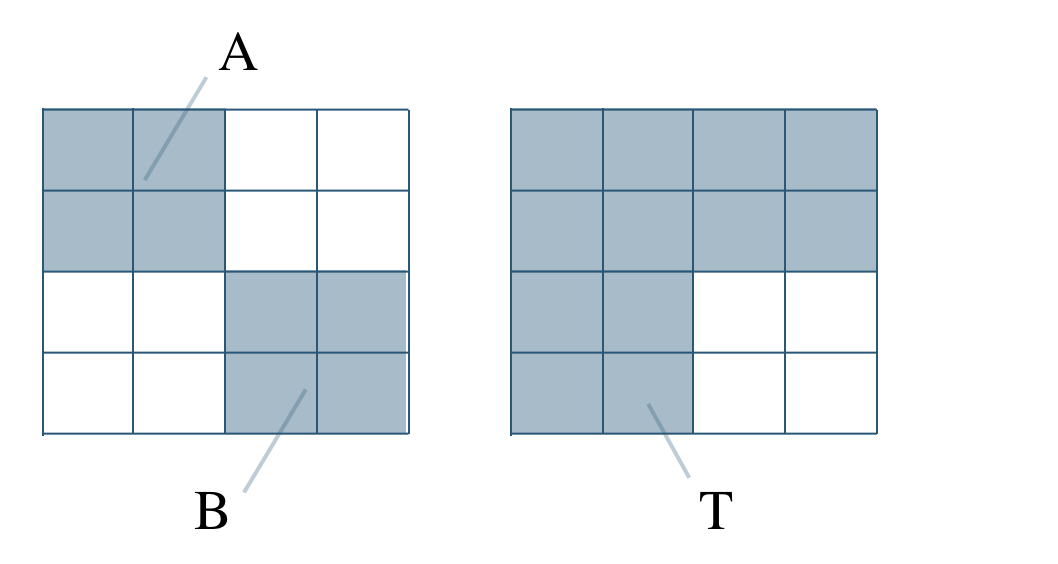
\({\rm T}\) は、
上２行の和 \({\rm 2S}\) と左２列の和 \({\rm 2S}\) から \({\rm A}\) を引いたものになるので、$$~~~{\rm T=2S+2S-A=4S-A}$$
また、\({\rm T}\) は、全体 \({\rm 4S}\) から \({\rm B}\) を引いたものでもあるので、$$~~~{\rm T=4S-B}$$
よって、$$\begin{eqnarray}~~~{\rm 4S-A}&=&{\rm 4S-B}\\[2pt]~~~{\rm A}&=&{\rm B}\end{eqnarray}$$したがって、
　左上の４つの数の和＝右下の４つの数の和
が成り立つ
同様に考えて、
　右上の４つの数の和＝左下の４つの数の和
が成り立つ