このページは、数研出版:新編数学A[714]
第2章 図形の性質
第2章 図形の性質

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介 高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
新編数学A 第1章 場合の数と確率
新編数学A 第2章 図形の性質
新編数学A 第3章 数学と人間の活動
第2章 図形の性質
第1節 平面図形
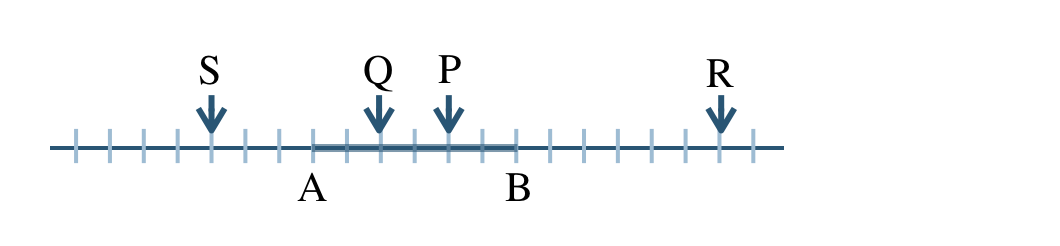
p.70 練習2$${\small (1)}~2:1$$$${\small (2)}~{ \frac{\,16\,}{\,3\,}}$$
p.70 練習3[証明]

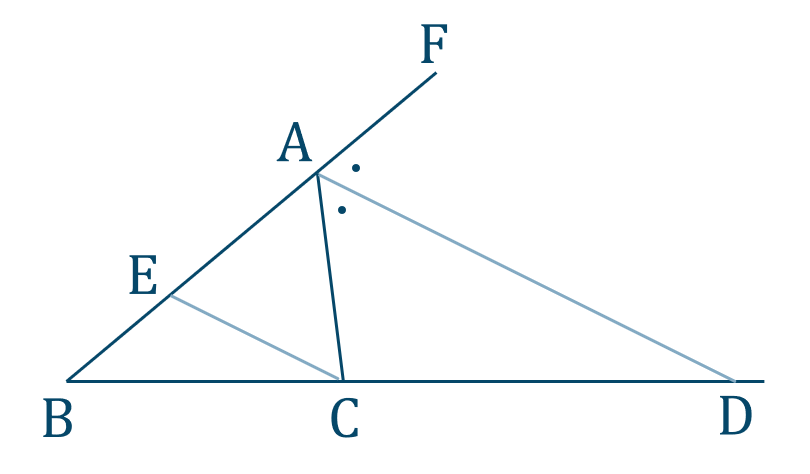
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\,//\, EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\,//\, EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\,//\, EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\,//\, EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
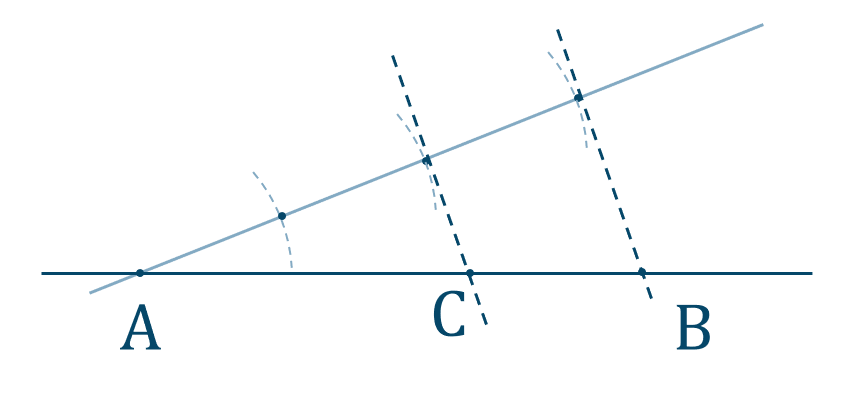
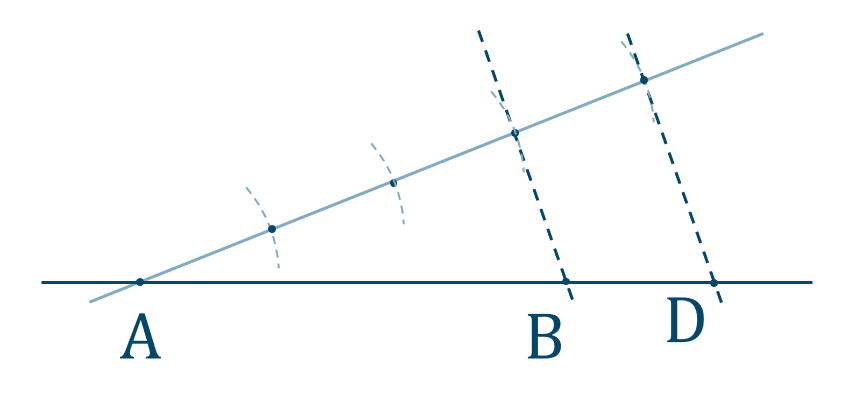
p.70 練習4$$~~~40$$→ 角の二等分線と比
p.72 練習5$${\small (1)}~40^{\circ}$$$${\small (2)}~100^{\circ}$$$${\small (3)}~20^{\circ}$$→ 三角形の外心
p.74 練習6$${\small (1)}~130^{\circ}$$$${\small (2)}~25^{\circ}$$$${\small (3)}~110^{\circ}$$→ 三角形の内心
p.75 練習7$${\small (1)}~5$$$${\small (2)}~4$$
p.77 練習8$${\small (1)}~1:3$$$${\small (2)}~1:3$$→ 三角形の重心
p.77 練習9$$~~~3:2$$
p.77 練習10$$~~~2:3$$→ チェバの定理
p.78 深める
p.79 練習11$${\small (1)}~1:2$$$${\small (2)}~5:4$$→ メネラウスの定理
p.79 練習12$${\small (1)}~3:1$$$${\small (2)}~1:2$$
p.80 研究 練習2[証明] \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) において、
他の角は \(\angle{\rm C}\) より小さい鋭角であるので、
\(\angle{\rm C}>\angle{\rm A}~,~\angle{\rm C}>\angle{\rm B}\)
三角形の辺と角の大小関係より、
\(c>a~,~c>b\)
したがって、\(c\) が最大の辺となるので、直角三角形では3辺のうち斜辺が最大である [終]
他の角は \(\angle{\rm C}\) より小さい鋭角であるので、
\(\angle{\rm C}>\angle{\rm A}~,~\angle{\rm C}>\angle{\rm B}\)
三角形の辺と角の大小関係より、
\(c>a~,~c>b\)
したがって、\(c\) が最大の辺となるので、直角三角形では3辺のうち斜辺が最大である [終]
p.82 練習13円の一部分上に任意の異なる3点 \({\rm A,B,C}\) をとる
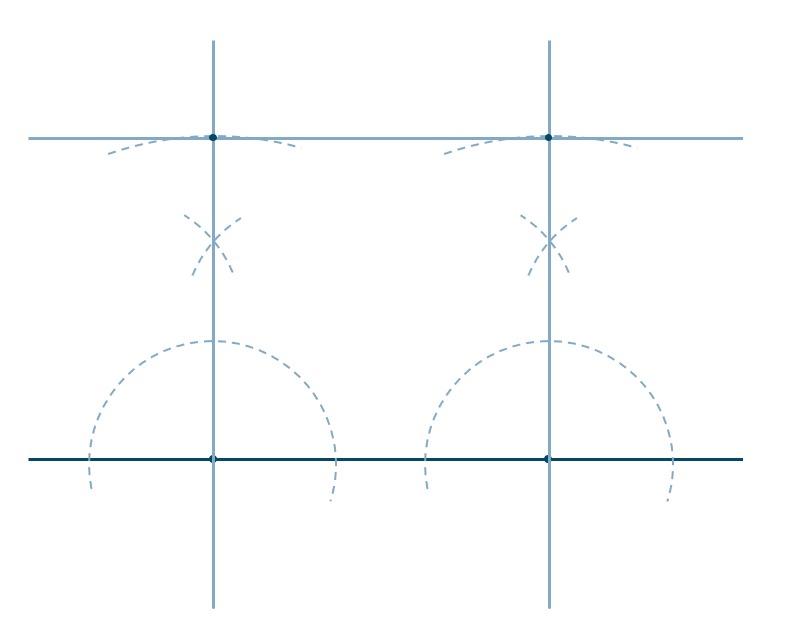
この円の中心は三角形 \({\rm ABC}\) の外心となるので、線分 \({\rm AB}\) と 線分 \({\rm BC}\) のそれぞれの垂直二等分線を引き、その交点が円の中心となる
この円の中心は三角形 \({\rm ABC}\) の外心となるので、線分 \({\rm AB}\) と 線分 \({\rm BC}\) のそれぞれの垂直二等分線を引き、その交点が円の中心となる
p.83 練習14$${\small (1)}~105^{\circ}$$$${\small (2)}~60^{\circ}$$$${\small (3)}~43^{\circ}$$→ 円周角と中心角
p.83 練習15\({\small (1)}\)対頂角より、
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
p.84 練習16$${\small (1)}~105^{\circ}$$$${\small (2)}~95^{\circ}$$→ 円に内接する四角形と角
p.85 練習17 ②、③
p.87 練習18$${\small (1)}~3$$$${\small (2)}~1$$→ 内接円と接線の条件
p.88 練習19$${\small (1)}~60^{\circ}$$$${\small (2)}~78^{\circ}$$$${\small (3)}~85^{\circ}$$→ 接弦定理
p.89 練習20$${\small (1)}~15$$$${\small (2)}~75$$→ 方べきの定理
p.90 練習21$${\small (1)}~6$$$${\small (2)}~\frac{\,5\,}{\,3\,}$$
p.90 練習22$$~~~2\sqrt{6}$$
p.93 練習23\({\small (1)}~\)[2]
\({\small (2)}~\)[1]
\({\small (3)}~\)[4]
\({\small (4)}~\)[3]
\({\small (5)}~\)[5]
→ 2つの円の位置関係と共通接線
\({\small (2)}~\)[1]
\({\small (3)}~\)[4]
\({\small (4)}~\)[3]
\({\small (5)}~\)[5]
→ 2つの円の位置関係と共通接線
p.93 練習24$$~~~60^\circ$$
p.94 練習25$$~~~\sqrt{26}$$
p.94 練習26$$~~~6$$→ 共通接線の長さ
p.96 練習28①より、\({\rm AB=AP}\)
②より、\({\rm AP=BC=PC}\)
2組の辺がそれぞれ等しいので、四角形 \({\rm ABCP}\) は平行四辺形となる
よって、\({\rm AB\,//\,PC}\) となり、直線 \({\rm PC}\) が \(l\) と平行となる
②より、\({\rm AP=BC=PC}\)
2組の辺がそれぞれ等しいので、四角形 \({\rm ABCP}\) は平行四辺形となる
よって、\({\rm AB\,//\,PC}\) となり、直線 \({\rm PC}\) が \(l\) と平行となる
p.99 研究 練習1\({\small (1)}~\)[証明] 正五角形 \({\rm ABCDE}\) は円に内接しており、\({\rm CD=BC}\) の同じ弦に対する円周角の定理より、
\(\angle{\rm CAD}=\angle{\rm FDC}=a\) …①
同様に、
\(\angle{\rm BAC}=\angle{\rm CBD}\)
\(=\angle{\rm ACE}=\angle{\rm ECD}=a\)
\(\triangle {\rm BFC}\) の \(\angle{\rm BFC}\) の外角の条件より、
\(\angle{\rm DFC}=\angle{\rm CBF}+\angle{\rm BCA}=2a\)
次に、弧 \({\rm AD}\) における円周角より、
\(\angle{\rm ACD}=\angle{\rm ACE}+\angle{\rm ECD}=2a\)
よって、
\(\angle{\rm ACD}=\angle{\rm DFC}\) …②
①と②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm DFC}\) は二等辺三角形より、
\({\rm CD=DF}=1\)
\(\triangle {\rm AFD}\) は二等辺三角形より、
\({\rm FD=FA}=1\)
よって、
\({\rm FC=AC-FA}=x-1\)
(1) より、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\)
よって、
\({\rm AC:DF=CD:FC}\)
したがって、
\(x:1=1:x-1\) [終]
\({\small (3)}~\)[証明] (2) より、
\(x:1=1:x-1\)
これより、$$\begin{eqnarray}~~~x(x-1)&=&1\\[2pt]~~~x^2-x-1&=&0\end{eqnarray}$$解の公式より、$$~~~x={ \frac{\,1\pm \sqrt{5}\,}{\,2\,}}$$ここで、\(x>0\) より、$$~~~x={ \frac{\,1+\sqrt{5}\,}{\,2\,}}$$また、\({\rm CD:AC}=1:x\) より、
\({\rm CD:AC}=1:{\large \frac{1+\sqrt{5}}{2}}\) [終]
\(\angle{\rm CAD}=\angle{\rm FDC}=a\) …①
同様に、
\(\angle{\rm BAC}=\angle{\rm CBD}\)
\(=\angle{\rm ACE}=\angle{\rm ECD}=a\)
\(\triangle {\rm BFC}\) の \(\angle{\rm BFC}\) の外角の条件より、
\(\angle{\rm DFC}=\angle{\rm CBF}+\angle{\rm BCA}=2a\)
次に、弧 \({\rm AD}\) における円周角より、
\(\angle{\rm ACD}=\angle{\rm ACE}+\angle{\rm ECD}=2a\)
よって、
\(\angle{\rm ACD}=\angle{\rm DFC}\) …②
①と②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm DFC}\) は二等辺三角形より、
\({\rm CD=DF}=1\)
\(\triangle {\rm AFD}\) は二等辺三角形より、
\({\rm FD=FA}=1\)
よって、
\({\rm FC=AC-FA}=x-1\)
(1) より、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\)
よって、
\({\rm AC:DF=CD:FC}\)
したがって、
\(x:1=1:x-1\) [終]
\({\small (3)}~\)[証明] (2) より、
\(x:1=1:x-1\)
これより、$$\begin{eqnarray}~~~x(x-1)&=&1\\[2pt]~~~x^2-x-1&=&0\end{eqnarray}$$解の公式より、$$~~~x={ \frac{\,1\pm \sqrt{5}\,}{\,2\,}}$$ここで、\(x>0\) より、$$~~~x={ \frac{\,1+\sqrt{5}\,}{\,2\,}}$$また、\({\rm CD:AC}=1:x\) より、
\({\rm CD:AC}=1:{\large \frac{1+\sqrt{5}}{2}}\) [終]
p.99 研究 練習2

p.100 研究 練習1[証明] \(\triangle {\rm ABB’}\) と \(\triangle {\rm ACC’}\) において、
\(\triangle {\rm ABC}\) と \(\triangle {\rm AB’C’}\) はともに正三角形より、\(\angle{\rm BAC}=\angle{\rm B’AC’}=60^\circ\) であり、
\(\angle{\rm BAB’}=60^\circ-\angle{\rm B’AC}\)
\(\angle{\rm CAC’}=60^\circ-\angle{\rm B’AC}\)
これより、
\(\angle{\rm BAB’}=\angle{\rm CAC’}\)…①
また、\({\rm AB=AC~,~AB’=AC’}\) より、
\({\rm AB:AB’=AC:AC’}\)…②
①、②より、2組の辺の比とその間の角がそれぞれ等しいので、
\(\triangle {\rm ABB’}\sim\triangle {\rm ACC’}\)
これより、
\(\angle{\rm ABB’}=\angle{\rm ACC’}\)
\(\angle{\rm ABB’}\) の大きさは点 \({\rm B’}\) が直線 \(n\) 上の点より一定で、\(\angle{\rm ACC’}\) の大きさも一定
したがって、正三角形の残りの頂点は直線上にある [終]
\(\triangle {\rm ABC}\) と \(\triangle {\rm AB’C’}\) はともに正三角形より、\(\angle{\rm BAC}=\angle{\rm B’AC’}=60^\circ\) であり、
\(\angle{\rm BAB’}=60^\circ-\angle{\rm B’AC}\)
\(\angle{\rm CAC’}=60^\circ-\angle{\rm B’AC}\)
これより、
\(\angle{\rm BAB’}=\angle{\rm CAC’}\)…①
また、\({\rm AB=AC~,~AB’=AC’}\) より、
\({\rm AB:AB’=AC:AC’}\)…②
①、②より、2組の辺の比とその間の角がそれぞれ等しいので、
\(\triangle {\rm ABB’}\sim\triangle {\rm ACC’}\)
これより、
\(\angle{\rm ABB’}=\angle{\rm ACC’}\)
\(\angle{\rm ABB’}\) の大きさは点 \({\rm B’}\) が直線 \(n\) 上の点より一定で、\(\angle{\rm ACC’}\) の大きさも一定
したがって、正三角形の残りの頂点は直線上にある [終]
p.100 研究 練習2
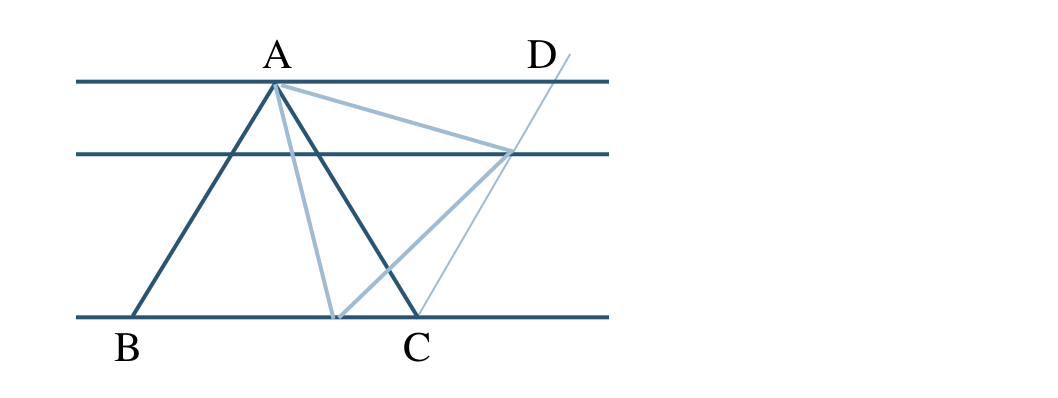
p.100 研究 練習3

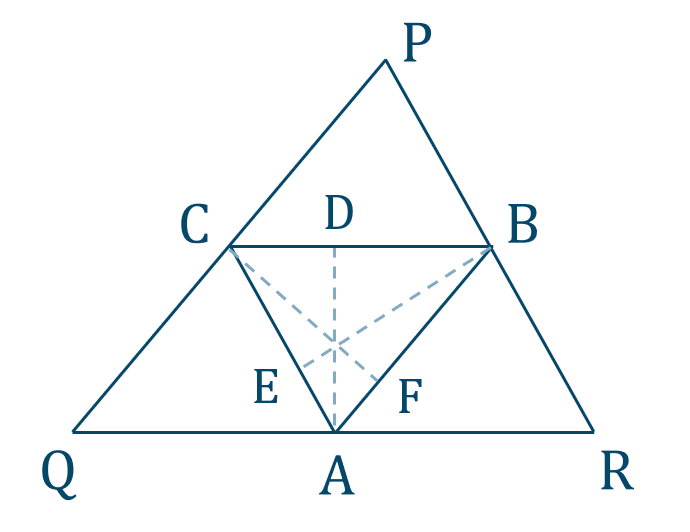
p.101 補充問題1[証明]

点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
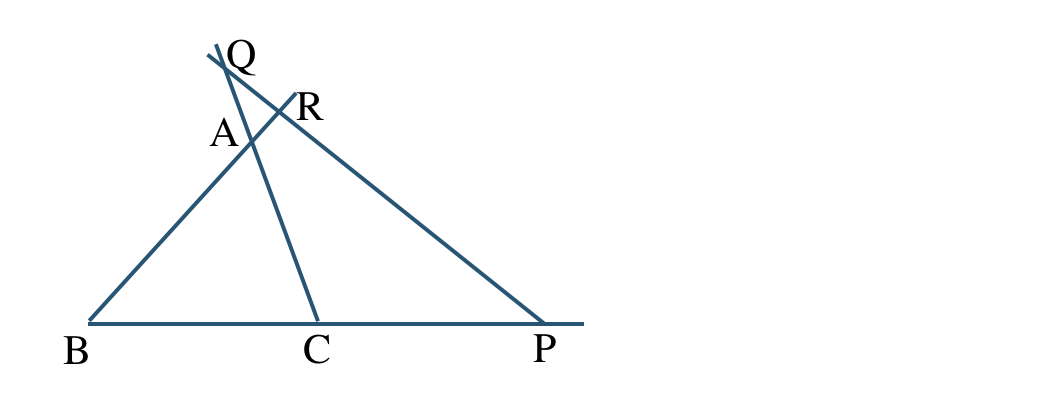
\({\rm CB\,//\, QR,CA\,//\, PR,AB\,//\, QP}\)
ここで、\({\rm CB\,//\, QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
\({\rm CB\,//\, QR,CA\,//\, PR,AB\,//\, QP}\)
ここで、\({\rm CB\,//\, QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
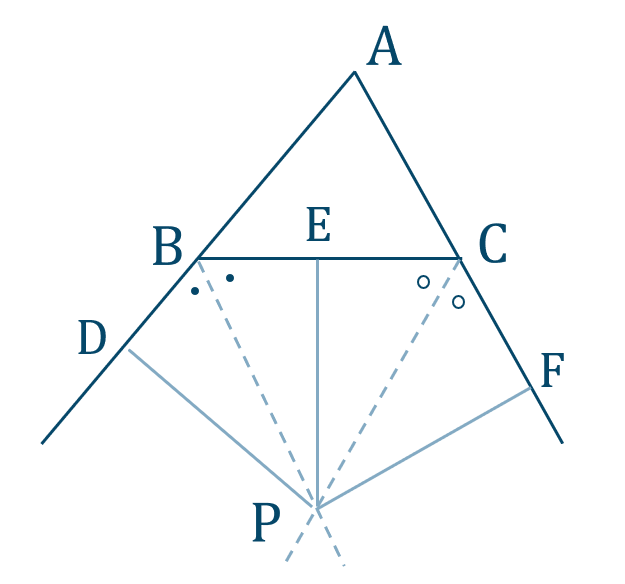
p.101 補充問題2[証明]

点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
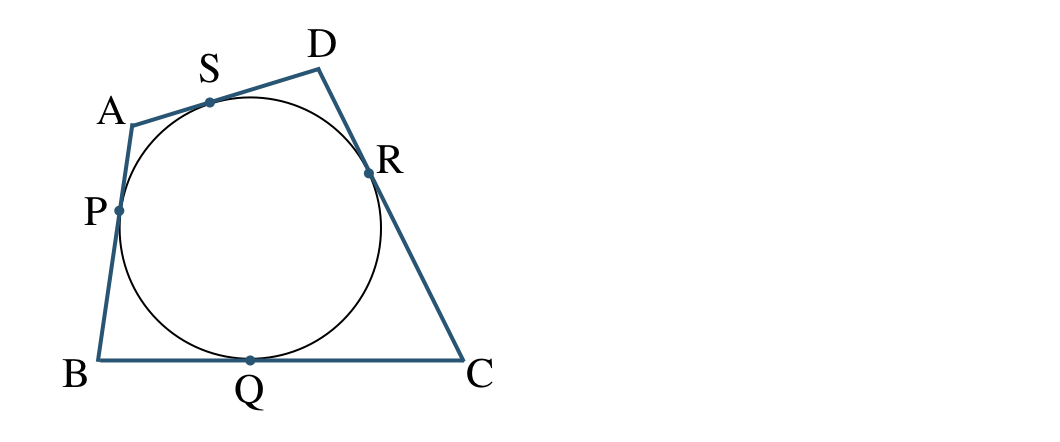
p.101 補充問題3[証明]

図のように、接点を \({\rm P~,~Q~,~R~,~S}\) とすると、
\({\rm AP=AS~,~BP=BQ}\)
\({\rm CQ=BQ~,~DR=DS}\)
よって、$$\begin{split}&{\rm AB+CD}\\[2pt]~~=~&{\rm (AP+BP)+(CR+DR)}\\[2pt]~~=~&{\rm AS+BQ+CQ+DS}\\[2pt]~~=~&{\rm (AS+DS)+(BQ+CQ)}\\[2pt]~~=~&{\rm AD+BC}\end{split}$$したがって、$$~~~{\rm AB+CD=BC+DA}$$[終]
図のように、接点を \({\rm P~,~Q~,~R~,~S}\) とすると、
\({\rm AP=AS~,~BP=BQ}\)
\({\rm CQ=BQ~,~DR=DS}\)
よって、$$\begin{split}&{\rm AB+CD}\\[2pt]~~=~&{\rm (AP+BP)+(CR+DR)}\\[2pt]~~=~&{\rm AS+BQ+CQ+DS}\\[2pt]~~=~&{\rm (AS+DS)+(BQ+CQ)}\\[2pt]~~=~&{\rm AD+BC}\end{split}$$したがって、$$~~~{\rm AB+CD=BC+DA}$$[終]
第2節 空間図形
p.103 練習32\({\small (1)}~\)辺CD、辺EF、辺GH
\({\small (2)}~\)辺FG、辺EH、辺CG、辺DH
\({\small (3)}~{\large ①}~90^{\circ}\)
\({\large ②}~45^{\circ}\)
\({\large ③}~90^{\circ}\)
→ 空間図形の位置関係
\({\small (2)}~\)辺FG、辺EH、辺CG、辺DH
\({\small (3)}~{\large ①}~90^{\circ}\)
\({\large ②}~45^{\circ}\)
\({\large ③}~90^{\circ}\)
→ 空間図形の位置関係
p.103 深める$$~~~60^\circ$$
p.104 練習33\({\small (1)}~\)[証明]
条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である[終]
\({\small (2)}~\)[証明]
(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である[終]
\({\small (2)}~\)[証明]
(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
p.105 練習34\({\small (1)}~\)

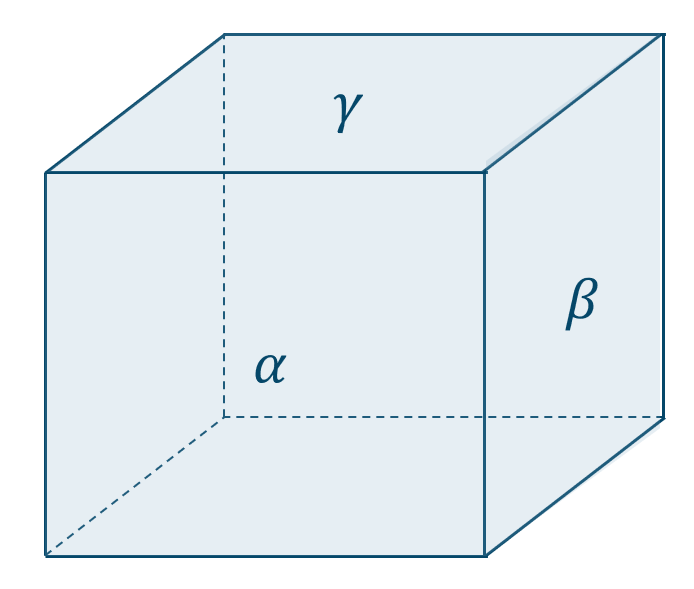
図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \,//\, \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)

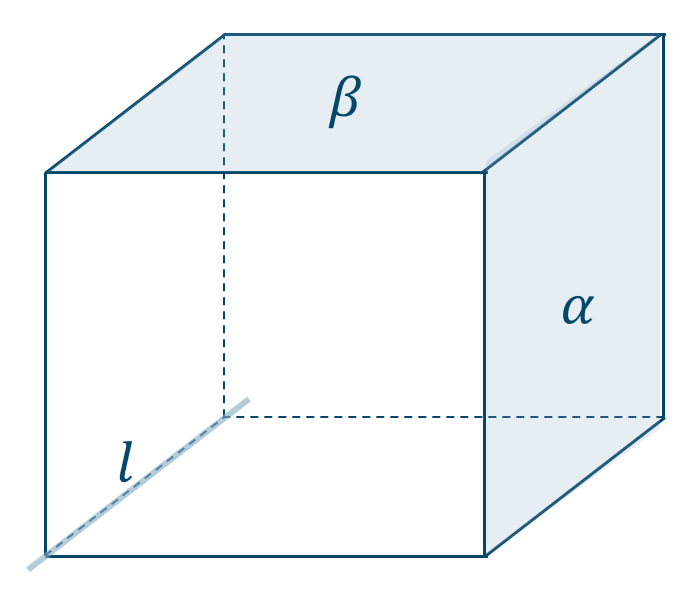
図より、\({\rm \alpha \,//\, l , \beta \,//\, l}\) としても \({\rm \alpha \,//\, \beta}\) でない
よって、正しくない
図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \,//\, \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)
図より、\({\rm \alpha \,//\, l , \beta \,//\, l}\) としても \({\rm \alpha \,//\, \beta}\) でない
よって、正しくない
p.107 練習35正四面体|\(\,4\,\)|正三角形|\(\,4\,\)|\(\,6\,\)
正六面体|\(\,6\,\)|正方形|\(\,8\,\)|\(\,12\,\)
正十二面体|\(\,12\,\)|正五角形|\(\,20\,\)|\(\,30\,\)
正二十面体|\(\,20\,\)|正三角形|\(\,12\,\)|\(\,30\,\)
正六面体|\(\,6\,\)|正方形|\(\,8\,\)|\(\,12\,\)
正十二面体|\(\,12\,\)|正五角形|\(\,20\,\)|\(\,30\,\)
正二十面体|\(\,20\,\)|正三角形|\(\,12\,\)|\(\,30\,\)
p.107 練習36それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
p.107 練習37面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\(14-24+12=2\)
\(14-24+12=2\)
p.108 練習38[証明]
\({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である [終]
\({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である [終]
p.109 研究 練習1$$~~~{ \frac{\sqrt{2}}{12}}a^3$$
p.111 補充問題4\({\small (1)}~\)

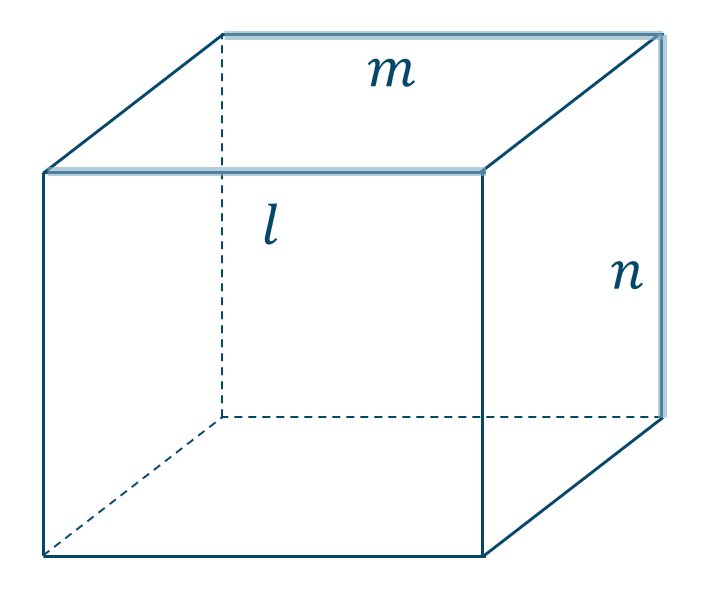
図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
章末問題 図形の性質
p.112 章末問題A5[証明]

\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \,//\, AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \,//\, AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \,//\, SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる [終]
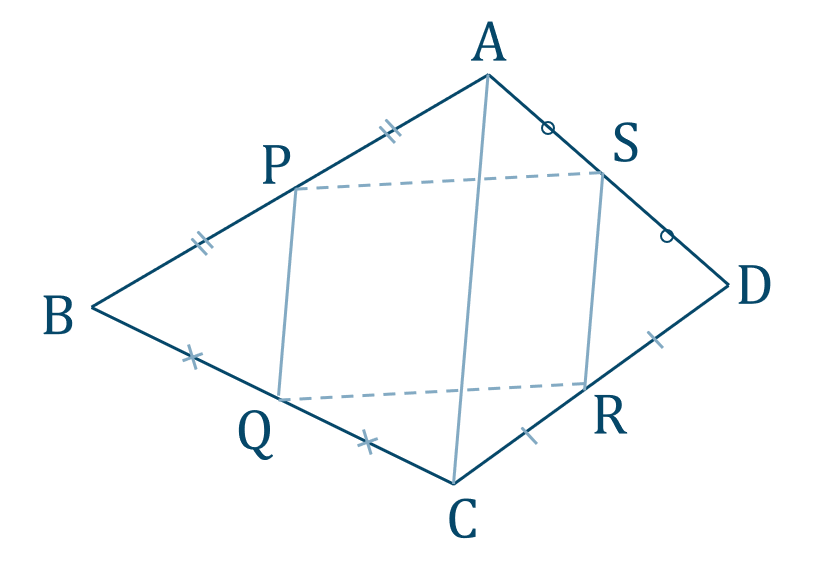
\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \,//\, AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \,//\, AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \,//\, SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる [終]
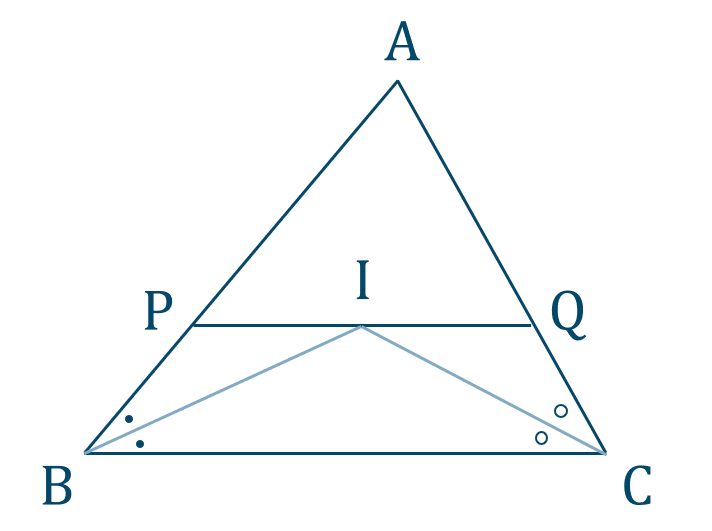
p.113 章末問題B6[証明]

点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \,//\, BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \,//\, BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \,//\, BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \,//\, BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
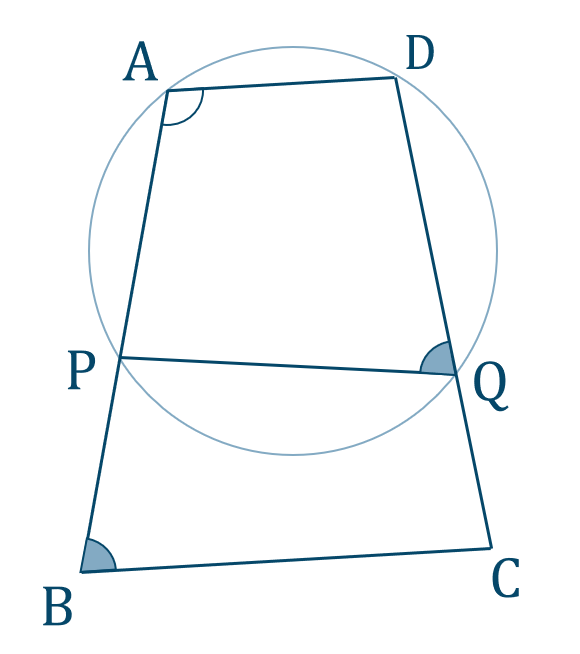
p.113 章末問題B7[証明]

\({\rm AD \,//\, BC}\) より、錯角との関係を用いて、
\(\angle{\rm BAD}+\angle{\rm ABC}=180^{\circ}\)
また、四角形 \(\rm APQB\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm PAD}+\angle{\rm DQP}=180^{\circ}\)
ここで、\(\angle{\rm BAD}=\angle{\rm PAD}\) であるので、
\(\angle{\rm ABC}=\angle{\rm DQP}\)
これより、四角形 \(\rm PBCQ\) において、内角と対角の外角が等しくなる
したがって、四角形 \(\rm PBCQ\) は円に内接する[終]
\({\rm AD \,//\, BC}\) より、錯角との関係を用いて、
\(\angle{\rm BAD}+\angle{\rm ABC}=180^{\circ}\)
また、四角形 \(\rm APQB\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm PAD}+\angle{\rm DQP}=180^{\circ}\)
ここで、\(\angle{\rm BAD}=\angle{\rm PAD}\) であるので、
\(\angle{\rm ABC}=\angle{\rm DQP}\)
これより、四角形 \(\rm PBCQ\) において、内角と対角の外角が等しくなる
したがって、四角形 \(\rm PBCQ\) は円に内接する[終]
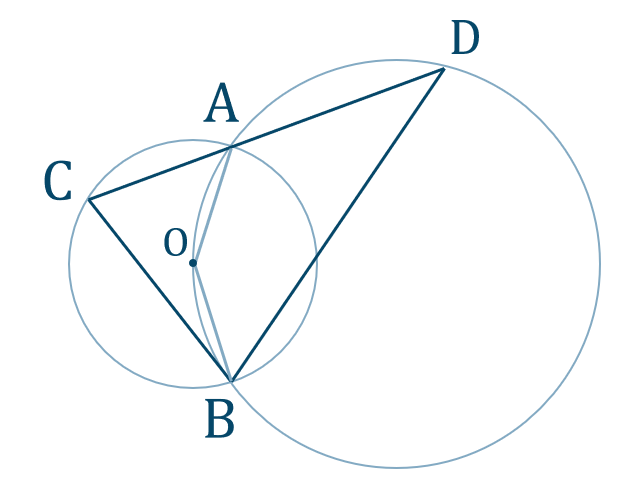
p.113 章末問題B8[証明]

\(\angle{\rm ACB}=x\) とすると、円周角と中心角の関係より、
\(\angle{\rm AOB}=2\angle{\rm ACB}=2x\)
また、四角形 \(\rm AOBD\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm ADB}=180^{\circ}-\angle{\rm AOB}=180^{\circ}-2x\)
次に \(\triangle{\rm DCB}\) の内角の和より、
\(\angle{\rm DBC}=180^{\circ}-(\angle{\rm DCB}+\angle{\rm CDB})\)
\(~~~~~=180^{\circ}-(x+180^{\circ}-2x)=x\)
よって、\(\angle{\rm DCB}=\angle{\rm DBC}=x\) となるので、\(\triangle{\rm DCB}\) は二等辺三角形となる[終]
\(\angle{\rm ACB}=x\) とすると、円周角と中心角の関係より、
\(\angle{\rm AOB}=2\angle{\rm ACB}=2x\)
また、四角形 \(\rm AOBD\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm ADB}=180^{\circ}-\angle{\rm AOB}=180^{\circ}-2x\)
次に \(\triangle{\rm DCB}\) の内角の和より、
\(\angle{\rm DBC}=180^{\circ}-(\angle{\rm DCB}+\angle{\rm CDB})\)
\(~~~~~=180^{\circ}-(x+180^{\circ}-2x)=x\)
よって、\(\angle{\rm DCB}=\angle{\rm DBC}=x\) となるので、\(\triangle{\rm DCB}\) は二等辺三角形となる[終]
p.113 章末問題B9\({\small (1)}~\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、

これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、
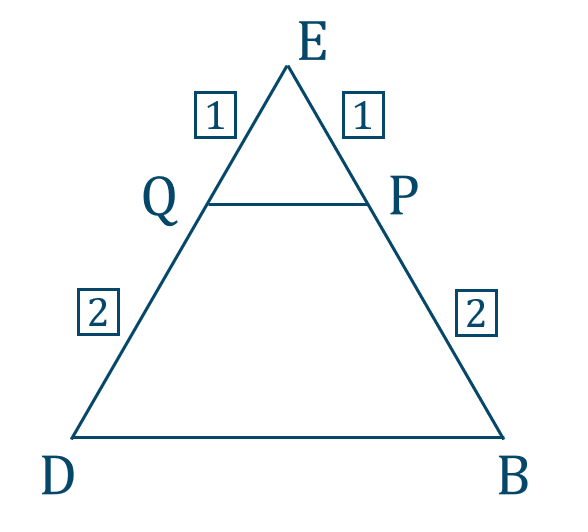
これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
次のページ「第3章 数学と人間の活動」