【新課程】数研出版：数学Ａ[712]

p.132 練習1\({\small (1)}~\)(例) \(100\)
\({\small (2)}~10\) の倍数となる

p.133 練習2$${\small (1)}~\pm1~,~\pm2~,~\pm3~,~\pm6~,~\pm9~,~\pm18$$$${\small (2)}~6~,~12~,~18~,~24~,~30$$→ 約数と倍数

p.134 練習3４桁の自然数 \(N\) の千の位を \(a\)、百の位を \(b\)、十の位を \(c\)、一の位を \(d\) とすると、$$\begin{eqnarray}~~~N&=&1000a+100b+10c+d\\[2pt]~~~&=&8\times125a+(100b+10c+d)\end{eqnarray}$$よって、\(N\) が \(8\) の倍数となるのは、
\(100b+10c+d\) が \(8\) の倍数であればよい
したがって、下３桁が \(8\) の倍数のときである

p.135 練習4$$~~~8$$→ 倍数判別法

p.135 練習5\({\small (1)}~\)偶数桁目の数の和は、$$~~~1+5+0+4+7=17$$奇数桁目の数の和は、$$~~~3+8+2+6+9=28$$これらの差は、$$~~~28-17=11$$これが \(11\) の倍数となるので、
\(1358024679\) は \(11\) の倍数となる
 
\({\small (2)}~7\)

p.136 練習6$$~~~2~,~3~,~5~,~7~,~11~,~13~,~17$$$$~~~,~19~,~23~,~29~,~31~,~37~,~41$$$$~~~,~43~,~47~,~53~,~59~,~61~,~67$$$$~~~,~71~,~73~,~79~,~83~,~89~,~97$$

p.136 深める２行目以降では、\(7\) で割った余りが \(1\) または \(5\) となる列に何度も現れる

p.137 練習7$${\small (1)}~2^5\cdot3$$$${\small (2)}~3^2\cdot5^2$$$${\small (3)}~2\cdot3^3\cdot7$$$${\small (4)}~2^2\cdot3\cdot5\cdot7^2$$→ 素因数分解

p.138 練習8$${\small (1)}~1~,~2~,~4~,~7~,~8~,~14~,~28~,~56$$$${\small (2)}~1~,~2~,~3~,~5~,~6~,~9~,~10$$$$~~~~~15~,~18~,~30~,~45~,~90$$

p.139 練習9\({\small (1)}~10\) 個
\({\small (2)}~16\) 個
\({\small (3)}~24\) 個
→ 約数の個数・平方数

p.139 練習10\({\small (1)}~\)奇数
\({\small (2)}~\)奇数
\({\small (3)}~\)(1) と (2) より、正の約数の個数が奇数であれば、ひっくり返された回数が奇数となり、裏向きのカードとなる
\(1\) 〜 \(15\) までの数を素因数分解し、正の約数の個数を調べると、
　\(1=1^1\) 正の約数 \(1\) 個
　\(2=2^1\) 正の約数 \(2\) 個
　\(3=3^1\) 正の約数 \(2\) 個
　\(4=2^2\) 正の約数 \(3\) 個
　\(5=5^1\) 正の約数 \(2\) 個
　\(6=2^1\cdot 3^1\) 正の約数 \(4\) 個
　\(7=7^1\) 正の約数 \(2\) 個
　\(8=2^3\) 正の約数 \(4\) 個
　\(9=3^2\) 正の約数 \(3\) 個
　\(10=2^1\cdot 5^1\) 正の約数 \(4\) 個
　\(11=11^1\) 正の約数 \(2\) 個
　\(12=2^2\cdot 3^1\) 正の約数 \(6\) 個
　\(13=13^1\) 正の約数 \(2\) 個
　\(14=2^1\cdot 7^1\) 正の約数 \(4\) 個
　\(15=3^1\cdot 5^1\) 正の約数 \(4\) 個
これより、正の約数の個数が奇数となるのは、
　\(1=1^2~,~4=2^2~,~9=3^2\)
これらで、\(n^2\) の形をした数だけである

p.140 練習11$${\small (1)}~1~,~2~,~3~,~4~,~5~,~6~,~10$$$$~~~~~12~,~15~,~20~,~30~,~60$$$${\small (2)}~1~,~2~,~3~,~6~,~8~,~9~,~12$$$$~~~~~18~,~24~,~36~,~72$$$${\small (3)}~a=12$$

p.141 練習12$${\small (1)}~6$$$${\small (2)}~126$$$${\small (3)}~12$$→ 最大公約数と最小公倍数

p.141 練習13$$~~~a=24$$

p.143 練習14$${\small (1)}~1260$$$${\small (2)}~3780$$$${\small (3)}~6300$$→ 最大公約数と最小公倍数

p.143 練習15　\(465\) 年後

p.144 練習16$${\small (1)}~4~~~11~~~18~~~25~~~32$$$$~~~~~39~~~46~~~53~~~60~~~67$$$$~~~~~74~~~81~~~88~~~95~~~102$$$${\small (2)}~4~~~1~~~3~~~0~~~2$$$$~~~~~4~~~1~~~3~~~0~~~2$$$$~~~~~4~~~1~~~3~~~0~~~2$$$${\small (3)}~53$$

p.145 練習17\({\small (1)}~\)商 \(4\)、余り \(5\)
\({\small (2)}~\)商 \(-4\)、余り \(1\)

p.146 練習18$${\small (1)}~0$$$${\small (2)}~1$$$${\small (3)}~2$$$${\small (4)}~0$$→ 除法の性質

p.147 練習19[証明]
\(70a+21b+15c\) を \(3\) で割った余りは、$$~~~70a+21b+15c=3(23a+7b+5c)+a$$これより、\(a\) となる
 
\(70a+21b+15c\) を \(5\) で割った余りは、$$~~~70a+21b+15c=5(14a+4b+3c)+b$$これより、\(b\) となる
 
\(70a+21b+15c\) を \(7\) で割った余りは、$$~~~70a+21b+15c=7(10a+3b+2c)+c$$これより、\(c\) となる
[終]

p.147 練習20$$~~~71$$

p.148 練習21$$~~~a=23~{\rm cm}$$
それぞれを素因数分解すると、
　\(391=17\times23~,~299=13\times23\)
よって、\(391\) と \(299\) の最大公約数である

p.149 練習22$${\small (1)}~19$$$${\small (2)}~21$$$${\small (3)}~1$$$${\small (4)}~47$$→ ユークリッドの互除法

p.150 練習23$$~~~\frac{\,1\,}{\,13\,}$$

p.150 練習24$$~~~\frac{\,8\,}{\,225\,}$$

p.151 練習25長方形 \({\rm IFHC}\)
[証明]$$\begin{eqnarray}~~~{\rm IF}&=&\sqrt{2}-1\\[2pt]~~~{\rm IC}&=&1-(\sqrt{2}-1)=2-\sqrt{2}\end{eqnarray}$$ここで、$$\begin{split}&{\rm IF:IC}\\[2pt]~~=~&\sqrt{2}-1:2-\sqrt{2}\\[3pt]~~=~&\frac{\,\sqrt{2}-1\,}{\,\sqrt{2}-1\,}:\frac{\,2-\sqrt{2}\,}{\,\sqrt{2}-1\,}\\[3pt]~~=~&1:\sqrt{2}\end{split}$$よって、$$~~~{\rm IF:IC=AD:AB}$$したがって、もとの長方形と相似である
[終]

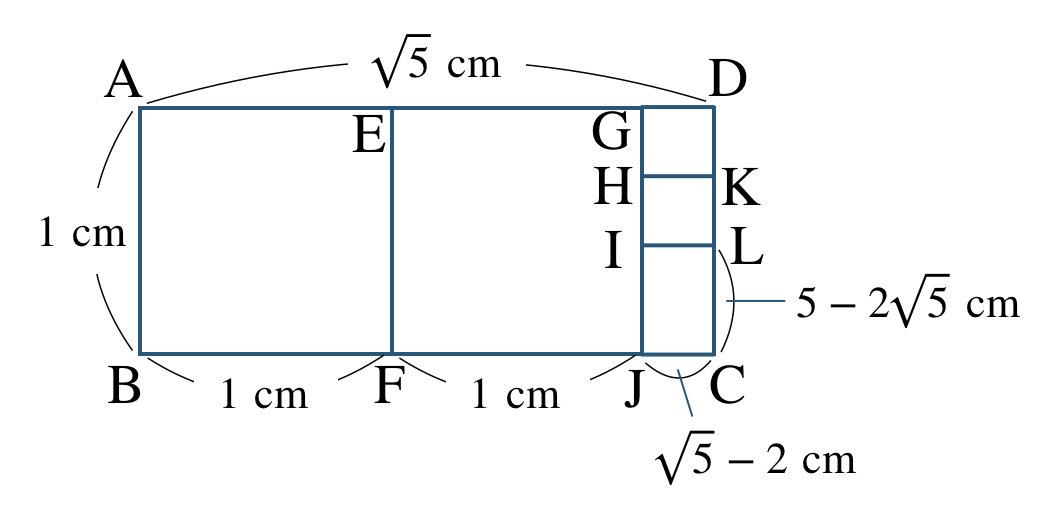
p.151 練習26

\(2<\sqrt{5}<3\) より、この長方形に１辺の長さ \(1\) の正方形を２個敷き詰めることができ、２辺の長さが \(1~,~\sqrt{5}-2\) の長方形が残る
この長方形には、１辺の長さが \(\sqrt{5}-2\) の正方形を２個敷き詰めると、２辺の長さが \(\sqrt{5}-2~,~5-2\sqrt{5}\) の長方形 \({\rm LIJC}\) が残る
これより、$$\begin{split}&{\rm LI:LC}\\[2pt]~~=~&\sqrt{5}-2:5-2\sqrt{5}\\[3pt]~~=~&\frac{\,\sqrt{5}-2\,}{\,\sqrt{5}-2\,}:\frac{\,5-2\sqrt{5}\,}{\,\sqrt{5}-2\,}\\[3pt]~~=~&1:\sqrt{5}\end{split}$$よって、もとの長方形と相似な長方形が現れ、この長方形を正方形で敷き詰めていく操作がいつまても終わらない
したがって、この長方形は１種類の正方形で敷き詰めることができないので、\(\sqrt{5}\) は無理数である

p.152 練習27(例)

p.154 練習28$${\small (1)}~x=5~,~y=-7$$$${\small (2)}~x=6~,~y=-20$$$${\small (3)}~x=21~,~y=30$$

p.155 練習29$${\small (1)}~x=-11~,~y=52$$$${\small (2)}~x=-88~,~y=17$$

p.155 深める$$~~~y=160$$

p.157 練習30\(k\) を整数とする$${\small (1)}~x=3k-1~,~y=-2k+1$$$${\small (2)}~x=3k-1~,~y=5k-2$$$${\small (3)}~x=9k-1~,~y=4k-1$$→ 不定方程式①

p.157 問1$${\small (1)}~x=5~,~y=-7$$$${\small (2)}~x=32k+20~,~y=-45k-28$$ただし、\(k\) は整数とする

p.157 練習31\(k\) を整数とする$$~~~x=15k-20~,~y=41k-55$$→ 不定方程式②（互除法）

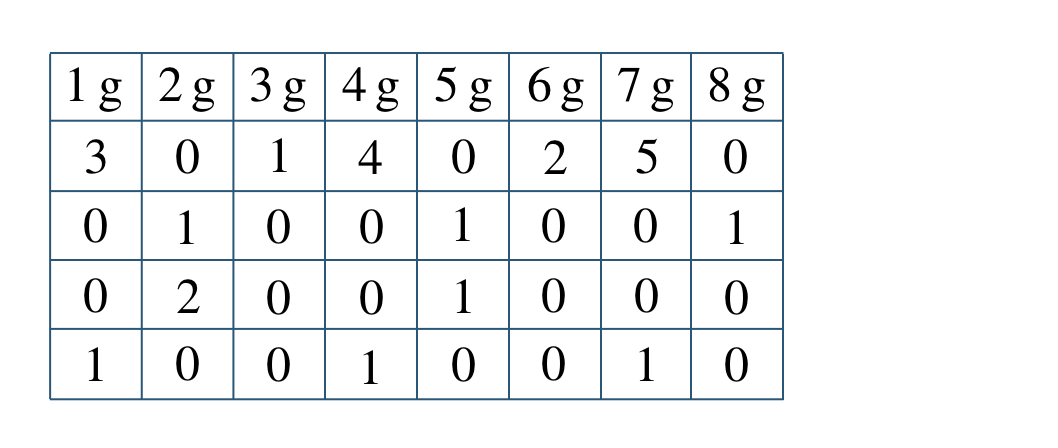
p.157 練習32左の皿に \(8~{\rm g}\) を \(2\) 個、右の皿に \(3~{\rm g}\) を \(2\) 個のせる

p.157 深める\(k\) を整数とする$$~~~x=4k+3~,~y=-3k-2$$この式の \(k\) を \(k-1\) とすると、$$\begin{eqnarray}~~~x&=&4(k-1)+3\\[2pt]~~~&=&4k-1\end{eqnarray}$$$$\begin{eqnarray}~~~y&=&-3(k-1)-2\\[2pt]~~~&=&-3k+1\end{eqnarray}$$例題２の解と等しくなる
したがって、整数 \(k\) 全体で考えると、すべての解が等しくなる

p.159 練習33$${\small (1)}~{\rm LXXXVII}$$$${\small (2)}~{\rm DCXXIX}$$

p.159 深める位が上がっても新しい数字(記号)が現れない

p.160 練習34$${\small (1)}~21$$$${\small (2)}~142$$$${\small (3)}~273$$$${\small (4)}~119$$→ n進法①（10進法で表す）

p.161 練習35$${\small (1)}~1000011_{(2)}$$$${\small (2)}~303_{(5)}$$$${\small (3)}~7414_{(8)}$$→ n進法②（n進法で表す）

p.163 練習36$${\small (1)}~(5~,~3)$$$${\small (2)}~(-7~,~-1)$$

p.163 練習37点 \({\rm O}\) から東へ \(12~{\rm m}\)、北へ \(9~{\rm m}\) 進んだ位置

p.163 深める点 \({\rm O}\) を中心に半径 \(13\) の円と、点 \({\rm A}\) を中心に半径 \(37\) の円をかき、これら２つの円の交点のうち北側( \(y>0\) )の点が \({\rm P}\) となる

p.165 練習38$${\small (1)}~(2~,~1~,~5)$$$${\small (2)}~(-3~,~2~,~-1)$$

p.165 練習39[証明]$$\begin{eqnarray}~~~{\rm OQ^2}&=&{\rm OA^2+AQ^2}\\[2pt]~~~&=&{\rm OA^2+OB^2}\\[2pt]~~~&=&a^2+b^2\end{eqnarray}$$また、\({\rm PQ^2=OC^2}=c^2\)
よって、\({\rm OP^2=OQ^2+PQ^2}\) より、$$\begin{eqnarray}~~~{\rm OP^2}&=&(a^2+b^2)+c^2\\[2pt]~~~&=&a^2+b^2+c^2\end{eqnarray}$$[終]

p.168 練習40先手が書いた◯の上下左右の4ヶ所のいずれかに書いたとき

p.169 練習41先手が中央に◯を置いたとき、
(ⅰ) 後手が先手の置いた◯の上下左右の4ヶ所のいずれかに置いたとき、

(ⅱ) 後手が四隅の4ヶ所のいずれかに置いたとき、

これより、先手が必ず勝つ方法はあるが、後手が必ず勝つ方法はない

p.170 練習42\({\small (1)}~~(1~,~5~,~9)~,~(1~,~6~,~8)\)
\({\small (2)}~\)\(1\) を含む \(3\) 個の数の和が \(15\) となるのは \(2\) 組しかない
四隅の \(4\) マスでは \(3\) 組必要になるので \(1\) は入らない

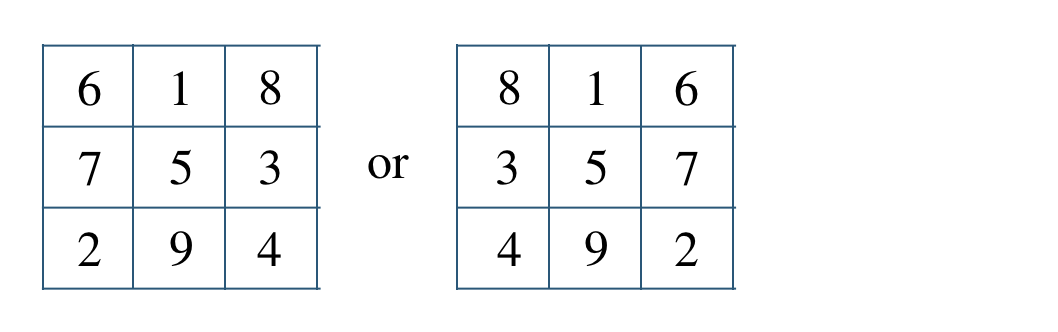
p.171 練習43\({\small (1)}~\)

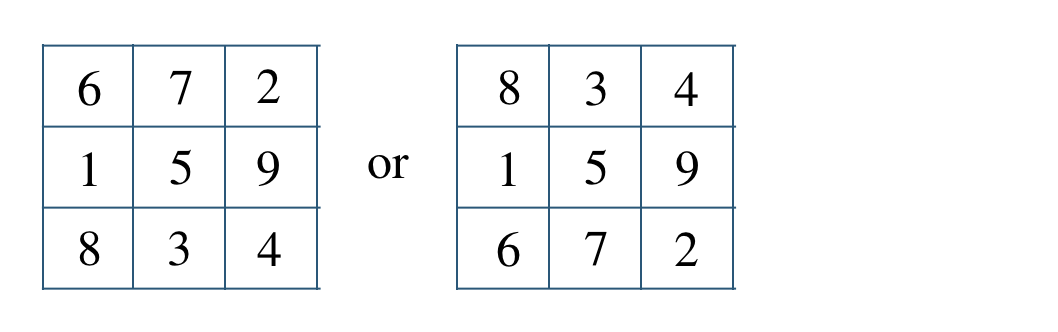
\({\small (2)}~\)

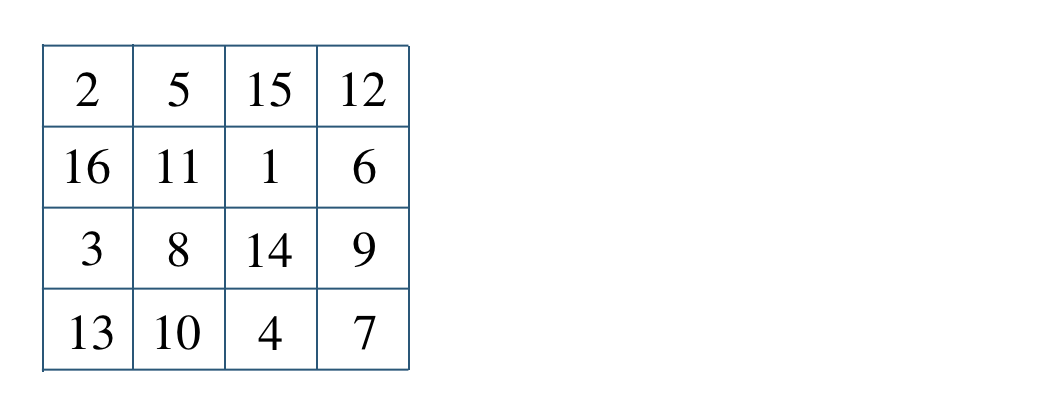
p.171 練習44$${\large ①}~~1+4+13+16=34$$$${\large ②}~~7+6+11+10=34$$$${\large ③}~~1+14+12+7=34$$$$~~~~~~15+4+6+9=34$$$$~~~~~~8+11+13+2=34$$$$~~~~~~10+5+3+16=34$$

p.172 練習45例18より、$$\begin{eqnarray}~~~{\rm 4S-N}&=&{\rm 4S-M}\\[2pt]~~~{\rm N}&=&{\rm M}\end{eqnarray}$$また、\({\rm M+N=2S}\) となるので、$$\begin{eqnarray}~~~\rm M+N&=&2S\\[2pt]~~~\rm M+M&=&2S\\[2pt]~~~\rm M&=& S=34\end{eqnarray}$$また、\({\rm N=M}\) より、$$~~~{\rm N=S}=34$$したがって、①と②の４つの数の和が魔法陣で \(34\) となる

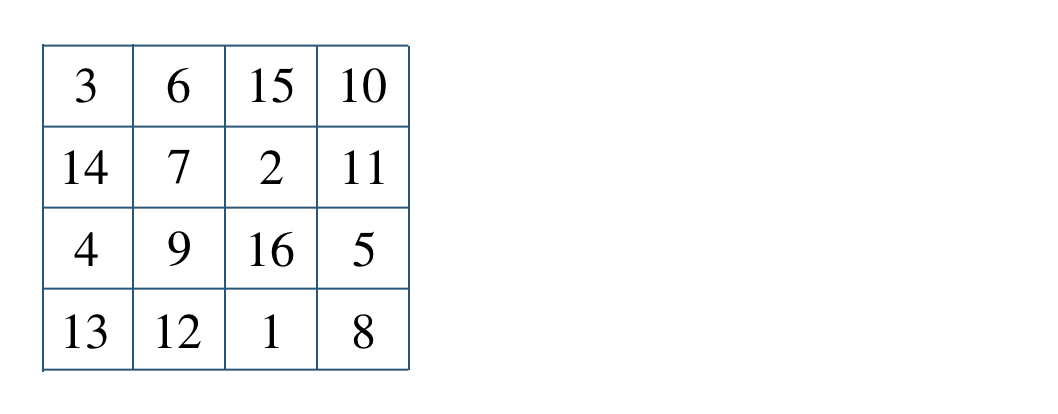
p.172 練習46$${\small (1)}~a=1~,~b=8~,~c=14$$

$${\small (2)}~a=15~,~b=2~,~c=8$$

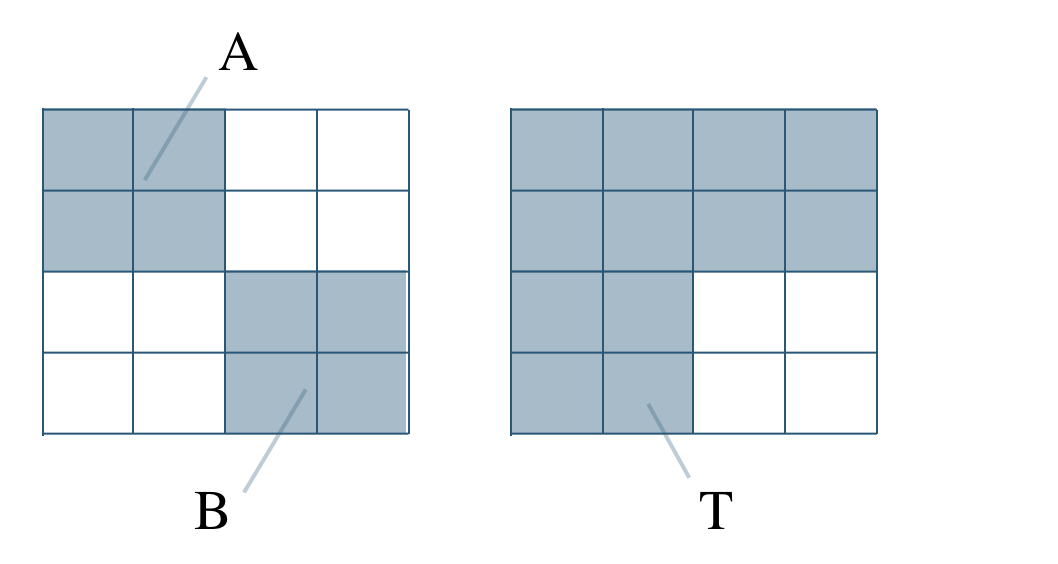
p.173 練習47\({\rm S}=34\) として、左上の４つの数の和を \({\rm A}\)、右下の４つの数の和を \({\rm B}\) とする
また、全体から右下の４つの数の和を除いた部分の和を \({\rm T}\) とすると、

\({\rm T}\) は、
上２行の和 \({\rm 2S}\) と左２列の和 \({\rm 2S}\) から \({\rm A}\) を引いたものになるので、$$~~~{\rm T=2S+2S-A=4S-A}$$
また、\({\rm T}\) は、全体 \({\rm 4S}\) から \({\rm B}\) を引いたものでもあるので、$$~~~{\rm T=4S-B}$$
よって、$$\begin{eqnarray}~~~{\rm 4S-A}&=&{\rm 4S-B}\\[2pt]~~~{\rm A}&=&{\rm B}\end{eqnarray}$$したがって、
　左上の４つの数の和＝右下の４つの数の和
が成り立つ
同様に考えて、
　右上の４つの数の和＝左下の４つの数の和
が成り立つ

p.175 補足 練習1[証明]
\(a\equiv c~({\rm mod~} m)\) より、整数 \(s\) を用いて、
　\(a-c=ms\)　…①
\(b\equiv d~({\rm mod~} m)\) より、整数 \(t\) を用いて、
　\(b-d=mt\)　…②
①-②より、
　(左辺)
\(=(a-c)-(b-d)\)
\(=(a-b)-(c-d)\)
　(右辺)
\(=ms-mt\)
\(=m(s-t)\)
したがって、
　\(a-b\equiv c-d~({\rm mod~} m)\) [終]

p.176 補足 練習2$${\small (1)}~1$$$${\small (2)}~2$$$${\small (3)}~9$$

p.178 補足 練習1$$~~~(x~,~y)=(-1~,~-3)~,~(3~,~1)$$$$~~~~~~~~~~,~(-3~,~7)~,~(-7~,~3)$$

p.178 補足 練習2$${\small (1)}~(x~,~y)=(0~,~2)~,~(-2~,~4)$$$${\small (2)}~(x~,~y)=(5~,~5)~,~(8~,~2)~,~(6~,~3)$$$$~~~~~~~~~~,~(2~,~-1)~,~(3~,~-3)~,~(0~,~0)$$→ 等式を満たす整数の組

p.178 補足 練習3$${\small (1)}~(x+3y+4)(2x+y+3)$$$${\small (2)}~(x~,~y)=(2~,~1)$$