【新課程】数研出版：数学Ａ[712]

p.6 練習1$${\small (1)}~\in$$$${\small (2)}~\notin$$$${\small (3)}~\in$$

p.7 練習2$${\small (1)}~{\rm F}=\{1~,~2~,~3~,~6~,~9~,~18\}$$$${\small (2)}~{\rm G}=\{10~,~12~,~14\}$$$${\small (3)}~{\rm H}=\{1~,~3~,~5~,~7~,~\cdots\}$$→ 集合の表し方と要素

p.7 深める\({\small (1)}~{\rm B}=\{x~|~x\) は \(99\) 以下の正の奇数 \(\}\)
\({\small (2)}~{\rm C}=\{5n~|~n=1~,~2~,~3~,~\cdots\}\)

p.8 練習3$${\small (1)}~{\rm B\subset A}$$$${\small (2)}~{\rm A=C}$$$${\small (3)}~{\rm A\subset D}$$

p.9 練習4$$~~~\phi~,~\{1\}~,~ \{2\}~,~ \{3\}$$$$~~~~~~~~,~\{1,2\}~,~ \{2,3\}~,~ \{1,3\}~,~ \{1,2,3\}$$→ 集合の包含関係と部分集合

p.9 練習5$$~~~{\rm A\cap B}=\{5,15\}$$$$~~~{\rm A\cup B}=\{1,3,5,7,9,10,11,13,15\}$$→ 共通部分と和集合

p.10 問1$$~~~{\rm A\cap B\cap C}=\{3,5\}$$$$~~~{\rm A\cup B\cup C}=\{1,2,3,4,5,7,11\}$$

p.10 練習6$$~~~{\rm A\cap B\cap C}=\{1,2,3,6\}$$$$~~~{\rm A\cup B\cup C}=\{1,2,3,4,5,6,7,9,12,18\}$$

p.11 練習7$${\small (1)}~\{1,4,6,8,9\}$$$${\small (2)}~\{1,2,6,7,8,9\}$$$${\small (3)}~\{1,6,8,9\}$$$${\small (4)}~\{1,2,4,6,7,8,9\}$$$${\small (5)}~\{4\}$$$${\small (6)}~\{2,7\}$$$${\small (7)}~\{1,2,3,5,6,7,8,9\}$$$${\small (8)}~\{1,3,4,5,6,8,9\}$$→ 補集合とド・モルガンの法則

p.11 練習8全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、

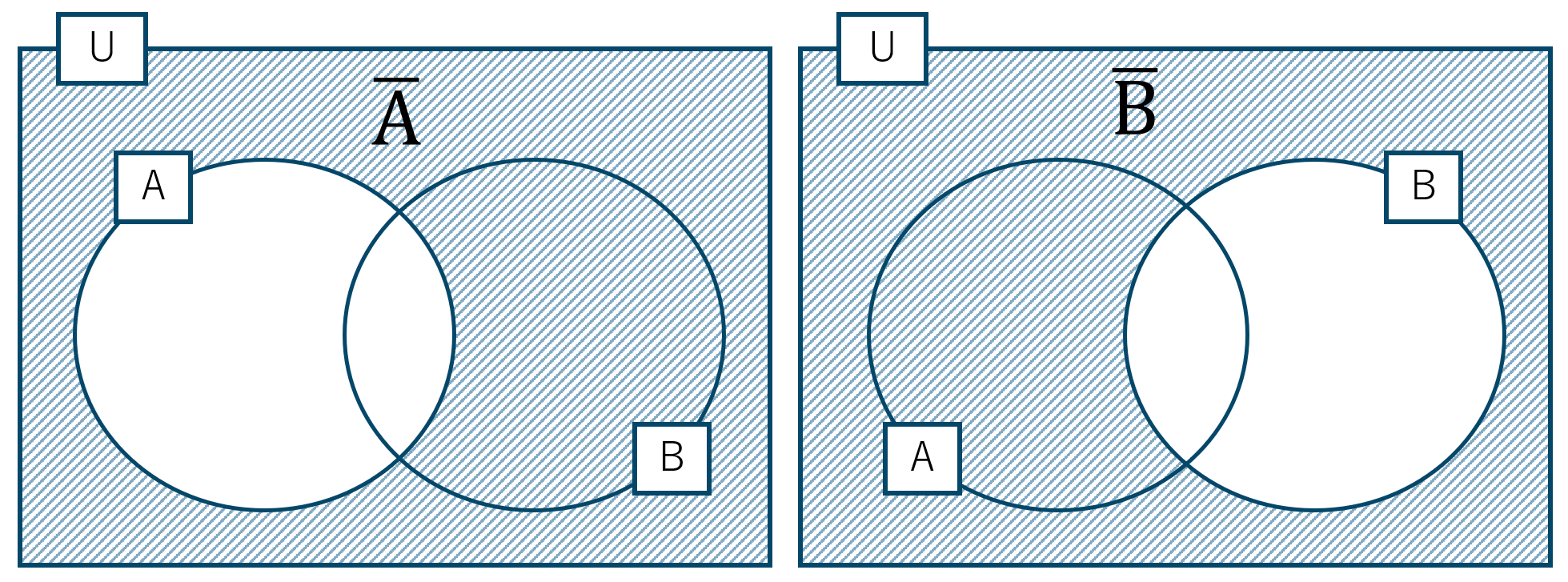
この２つの和集合となるので、

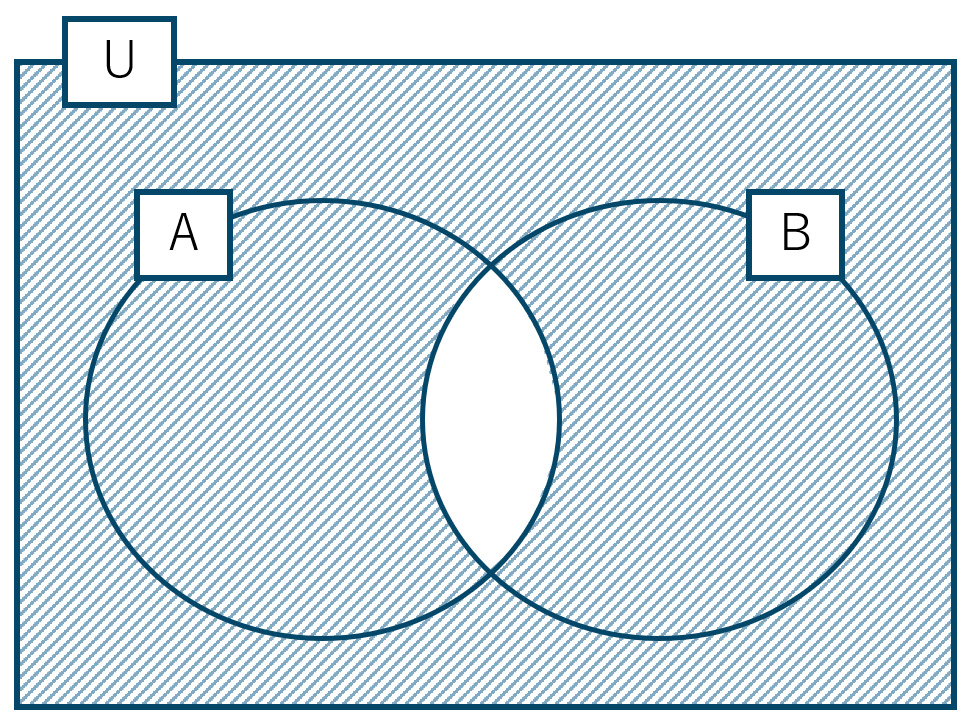
これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、$$~~~\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}$$

p.11 練習9[証明]$$\begin{eqnarray}~~~{\rm U}&=&\{1,2,3,4,5,6,7,8,9\}\\[2pt]~~~{\rm A}&=&\{2,4,6,8\}\\[2pt]~~~{\rm B}&=&\{3,6,9\}\\[2pt]~~~{\rm \overline {A}}&=&\{1,3,5,7,9\}\\[2pt]~~~{\rm \overline {B}}&=&\{1,2,4,5,7,8\}\end{eqnarray}$$これらより、$$~~~{\rm A\cup B}=\{2,3,4,6,8,9\}$$この否定は、$$~~~{\rm \overline {A\cup B}}=\{1,5,7\}$$また、$$~~~{\rm \overline {A}\cap \overline {B}}=\{1,5,7\}$$したがって、$$~~~{\rm \overline {A\cup B}}={\rm \overline {A}\cap \overline {B}}$$次に、$$~~~{\rm A\cap B}=\{6\}$$この否定は、$$~~~{\rm \overline {A\cap B}}=\{1,2,3,4,5,7,8,9\}$$また、$$~~~{\rm \overline {A}\cup \overline {B}}=\{1,2,3,4,5,7,8,9\}$$したがって、$$~~~{\rm \overline {A\cap B}}={\rm \overline {A}\cup \overline {B}}$$[終]

p.14 練習1$$~~~n({\rm A})=4~,~n({\rm B})=3$$

p.15 練習2$$~~~24$$→ 集合の要素の個数

p.16 練習3　\(134\) 個

p.16 深める　\(27\) 個

p.17 問1　\(11\) 人

p.17 練習4$${\small (1)}~10$$$${\small (2)}~13$$$${\small (3)}~5$$→ 補集合の要素の個数

p.18 研究 練習1[証明] 左辺は、$$\begin{split}&n({\rm A\cup B\cup C})\\[2pt]~~=~&a+b+c+d+e+f+g\end{split}$$また、右辺は、$$\begin{eqnarray}~~~n({\rm A})&=&a+d+g+f\\[2pt]~~~+n({\rm B})&=&b+d+g+e\\[2pt]~~~+n({\rm C})&=&c+f+g+e\\[2pt]~~~-n({\rm A\cap B})&=&-(d+g)\\[2pt]~~~-n({\rm B\cap C})&=&-(g+e)\\[2pt]~~~-n({\rm A\cap C})&=&-(g+f)\\[2pt]~~~+n({\rm A\cap B\cap C})&=&g\end{eqnarray}$$これらの和は、\(a+b+c++d+e+f+g\)
したがって、
$$\begin{split}&n({\rm A\cup B\cup C})\\[2pt]~~=~&n({\rm A})+n({\rm B})+n({\rm C})\\[2pt]&~~~~~~-n({\rm A\cap B})-n({\rm B\cap C})-n({\rm A\cap C})\\[2pt]&~~~~~~~~~~+n({\rm A\cap B\cap C})\end{split}$$[終]

p.18 研究 練習2　\(74\)
→ ３つの集合の要素の個数

p.20 練習5　\(18\)

p.20 練習6　\(21\)

p.20 深める樹形図をかくとき、
　１番目→２番目→３番目や大→中→小
と順番を変えないで数える

p.21 練習7　\(7\)

p.21 問2　\(9\)

p.21 練習8　\(6\)

p.22 練習9　\(35\)

p.22 問3　\(216\)

p.22 練習10　\(27\)
→ 和の法則と積の法則

p.22 練習11$${\small (1)}~12$$$${\small (2)}~12$$

p.23 練習12$${\small (1)}~12~,~195$$$${\small (2)}~18~,~868$$→ 約数の個数と展開式の項の個数

p.25 練習13$${\small (1)}~504$$$${\small (2)}~2520$$$${\small (3)}~6$$→ 順列と階乗の記号

p.25 練習14$${\small (1)}~210$$$${\small (2)}~3024$$

p.26 練習15$${\small (1)}~120$$$${\small (2)}~5040$$$${\small (3)}~40320$$→ 文字の順列

p.27 練習16　\(1680\)

p.27 問4　\(12\)

p.27 練習17$${\small (1)}~720$$$${\small (2)}~144$$

p.28 練習18$${\small (1)}~144$$$${\small (2)}~156$$→ 数字の順列

p.28 深める６個の数字から４個を取って並べる順列は、$$~~~{}_{ 6 } {\rm P}_{ 4 }=6\cdot5\cdot4\cdot3=360$$この中で４桁の整数とならないのは、千の位の数が \(0\) のときで、残りの百、十、一の位に５個の数字から３個取って並べるから、$$~~~{}_{ 5 } {\rm P}_{ 3 }=5\cdot4\cdot3=60$$したがって、求める整数の個数は、$$~~~360-60=300$$答えは \(300\) となる

p.30 練習19　\(120\)
→ 円順列とじゅず順列

p.30 問5　\(12\)

p.30 練習20　\(144\)
→ 条件付き円順列

p.31 練習21　\(64\)

p.31 練習22$${\small (1)}~243$$$${\small (2)}~120$$→ 重複を許す順列

p.31 練習23　\(128\)

p.33 練習24$${\small (1)}~35$$$${\small (2)}~15$$$${\small (3)}~4$$$${\small (4)}~1$$

p.33 問6[証明] \(n\) 個のもののなかから \(r\) 個取り出す組合せは、\({}_{n}{\rm C}_{r}\)
\(n\) 個のもののなかに特定の \(a\) があるとき、
(ⅰ) 取り出した \(r\) 個に特定の \(a\) を含む場合
\(a\) は取り出すのが確定しているので、それ以外の \(n-1\) 個のもののなかから \(r-1\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r-1}$$(ⅱ) 取り出した \(r\) 個に特定の \(a\) を含まない場合
\(a\) 以外の \(n-1\) 個のもののなかから \(r\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r}$$これらは同時に起こらないので和の法則より、$$~~~{}_{n}{\rm C}_{r}={}_{n-1}{\rm C}_{r-1}+{}_{n-1}{\rm C}_{r}$$[終]

p.34 練習25$${\small (1)}~9$$$${\small (2)}~21$$$${\small (3)}~560$$→ 組合せの記号

p.34 練習26　\(120\)

p.34 練習27$${\small (1)}~56$$$${\small (2)}~70$$$${\small (3)}~20$$→ 図形と組合せ

p.35 練習28$${\small (1)}~210$$$${\small (2)}~460$$→ 代表を選ぶ

p.35 練習29　\(60\)
→ 図形と組合せ

p.35 深める大人１人、子ども４人のとき、$$~~~{}_{ 10 } {\rm C}_{ 1 }\times{}_{ 6 } {\rm C}_{ 4 }=160$$大人２人、子ども３人のとき、$$~~~{}_{ 10 } {\rm C}_{ 1 }\times{}_{ 6 } {\rm C}_{ 3 }=900$$大人３人、子ども２人のとき、$$~~~{}_{ 10 } {\rm C}_{ 3 }\times{}_{ 6 } {\rm C}_{ 2 }=1800$$大人４人、子ども１人のとき、$$~~~{}_{ 10 } {\rm C}_{ 4 }\times{}_{ 6 } {\rm C}_{ 1 }=1260$$大人５人のとき、$$~~~{}_{ 10 } {\rm C}_{ 5 }=252$$よって、$$\begin{split}&150+900+1800+1260+252\\[2pt]~~=~&4362\end{split}$$したがって、\(4362\) 通りとなる

p.36 練習30$${\small (1)}~1680$$$${\small (2)}~280$$$${\small (3)}~378$$→ ３つのグループに分ける

p.37 深める\({\small (1)}~\)６個の文字の順列より、$$~~~{}_{ 6 } {\rm P}_{ 6 }=6!=720$$よって、\(720\) 通りとなる
 
\({\small (2)}~\)\(a_1~,~a_2~,~a_3\) の区別をなくすと、
\(a_1~,~a_2~,~a_3\) の区別があるときの順列である$$~~~{}_{ 3 } {\rm P}_{ 3 }=3!=6$$この \(6\) 通りがすべて \(a\) だけの \(1\) 通りになる
よって、\(720\) から割ると、$$~~~720\div6=120$$また、\(b_1~,~b_2\) の区別をなくすと、
\(b_1~,~b_2\) の区別があるときの順列である$$~~~{}_{ 2 } {\rm P}_{ }=2!=2$$この \(2\) 通りがすべて \(b\) だけの \(1\) 通りになる
よって、\(120\) をさらに \(2\) で割ると、$$~~~120\div2=60$$したがって、\(60\) 通りとなる

p.38 問7　\(210\)

p.38 練習31　\(3360\)
→ 同じものを含む順列

p.38 練習32$${\small (1)}~462$$$${\small (2)}~150$$$${\small (3)}~312$$→ 最短経路問題

p.40 研究 練習1　\(120\)

p.40 研究 練習2$${\small (1)}~286$$$${\small (2)}~84$$→ 重複組合せ

p.40 研究 練習3$${\small (1)}~66$$$${\small (2)}~36$$→ 等式を満たす自然数の組合せ

p.44 問8　Ａ：\(\{(\) 裏 \(,\) 裏 \()\}\)
　Ｂ：\(\{(\) 表 \(,\) 表 \()\}~,~\{(\) 表 \(,\) 裏 \()\}~,~\{(\) 裏 \(,\) 表 \()\}\)

p.44 練習33\({\small (1)}~\)
　\(\{(a_1,a_2), (a_1,b_1), (a_1,b_2), (a_1,b_3), (a_2,b_1)\)
　　\((a_2,b_2), (a_2,b_3), (b_1,b_2), (b_1,b_3), (b_2,b_3)\}\)
\({\small (2)}~\)
　\(\{(a_1,b_1), (a_1,b_2), (a_1,b_3)\)
　　\((a_2,b_1),(a_2,b_2), (a_2,b_3)\}\)

p.45 練習34$$~~~ \frac{\,3\,}{\,25\,}$$

p.46 練習35$$~~~ \frac{\,1\,}{\,2\,}$$→ 確率の基本

p.46 練習36　目の和が \(7\) の事象 \({\large \frac{\,1\,}{\,6\,}}\)
→ さいころの確率

p.47 練習37$${\small (1)}~ \frac{\,1\,}{\,2\,}$$$${\small (2)}~\frac{\,1\,}{\,6\,}$$→ ボールを取り出す確率

p.47 練習38$$~~~\frac{\,2\,}{\,5\,}$$→ 一列に並べる確率

p.49 問9$$\begin{eqnarray}~~~{\rm A\cap B}&=&\{1,2,3\}\\[2pt]~~~{\rm A\cup B}&=&\{1,2,3,4,6\}\end{eqnarray}$$$$~~~\frac{\,1\,}{\,2\,}~,~\frac{\,5\,}{\,6\,}$$

p.49 練習39$$~~~\frac{\,1\,}{\,6\,}~,~\frac{\,2\,}{\,3\,}$$→ 和事象と排反事象

p.49 練習40　\({\rm A}\) と \({\rm D}\)、\({\rm C}\) と \({\rm D}\)

p.51 練習41$$~~~ \frac{\,5\,}{\,57\,}$$

p.51 練習42$$~~~\frac{\,7\,}{\,36\,}$$→ 和事象と排反事象

p.52 問10$$~~~\frac{\,4\,}{\,13\,}$$

p.52 練習43$$~~~\frac{\,2\,}{\,9\,}$$

p.53 練習44$$~~~ \frac{\,11\,}{\,50\,}$$→ 和事象と排反事象

p.54 練習45$${\small (1)}~ \frac{\,11\,}{\,36\,}$$$${\small (2)}~ \frac{\,5\,}{\,6\,}$$→ 余事象の確率

p.56 練習46\({\small (1)}~\)独立である
\({\small (2)}~\)独立でない

p.58 練習47$${\small (1)}~\frac{\,1\,}{\,3\,}$$$${\small (2)}~\frac{\,1\,}{\,6\,}$$

p.58 練習48$$~~~0.95~~~\left(=\frac{\,19\,}{\,20\,}\right)$$

p.59 練習49$${\small (1)}~\frac{\,29\,}{\,50\,}$$$${\small (2)}~ \frac{\,21\,}{\,50\,}$$

p.60 練習50$${\small (1)}~\frac{\,1\,}{\,12\,}$$$${\small (2)}~\frac{\,7\,}{\,8\,}$$→ 独立試行の確率

p.62 練習51$$~~~\frac{\,625\,}{\,3888\,}$$→ 反復試行の確率②（さいころ）

p.62 練習52$${\small (1)}~\frac{\,1053\,}{\,3125\,}$$$${\small (2)}~\frac{\,288\,}{\,3125\,}$$

p.63 練習53$$~~~ \frac{\,80\,}{\,243\,}$$→ 点が動く確率

p.65 練習54$$~~~ \frac{\,3\,}{\,8\,}$$

p.66 練習55$$~~~0.6~~\left(=\frac{\,3\,}{\,5\,}\right)$$$$~~~0.75~~\left(=\frac{\,3\,}{\,4\,}\right)$$→ 条件付き確率

p.66 練習56$$~~~\frac{\,3\,}{\,4\,}$$

p.67 練習57$$~~~\frac{\,3\,}{\,28\,}$$

p.67 練習58$$~~~\frac{\,1\,}{\,21\,}$$

p.68 練習59$${\small (1)}~ \frac{\,1\,}{\,3\,}$$$${\small (2)}~ \frac{\,10\,}{\,21\,}$$→ 確率の乗法定理

p.68 深める$$~~~\frac{\,3\,}{\,20\,}$$

p.69 練習60$$~~~\frac{\,2\,}{\,3\,}$$

p.69 練習61$${\small (1)}~\frac{\,28\,}{\,75\,}$$$${\small (2)}~\frac{\,47\,}{\,75\,}$$

p.71 研究 練習1$$~~~\frac{\,9\,}{\,59\,}$$

p.74 練習62$$~~~\frac{\,3\,}{\,2\,}$$

p.75 練習63$$~~~5$$

p.75 練習64　［２］

p.76 練習65　得である