数研出版：改訂版新編数学Ａ

p.5
練習1
\({\small (1)}~\in\)　\({\small (2)}~\notin\)　\({\small (3)}~\notin\)

p.6
練習2
\({\small (1)}~{\rm A}=\{1,2,3,4,6,12\}\)
\({\small (2)}~{\rm B}=\{1,3,5,7,\cdots,29\}\)

p.6
練習3
\({\small (1)}~{\rm A}=\{3,6,9,12,15,18\}\)
\({\small (2)}~{\rm B}=\{1,3,5,7,\cdots\}\)
→ 集合の表し方と要素

p.7
練習4
\({\small (1)}~\rm A\subset B\)　\({\small (2)}~\rm C=D\)　\({\small (3)}~\rm P\supset Q\)

p.7
練習5
\({\small (1)}~\phi,\{1\},\{2\},\{1,2\}\)
\({\small (2)}~\phi,\{a\},\{b\},\{c\}\)
\(~~~~~~\{a,b\},\{b,c\},\{a,c\},\{a,b,c\}\)
→ 集合の包含関係と部分集合

p.8
練習6
\({\small (1)}~\{2,4,6\}\)
\({\small (2)}~\{1,2,3,4,5,6,7,8\}\)
\({\small (3)}~\phi\)
\({\small (4)}~\{1,2,3,4,6,8\}\)
→ 共通部分と和集合

p.8
練習7
\({\small (1)}~\{2,3\}\)
\({\small (2)}~\{1,2,3,4,5,6,7,11,12,13,17,19\}\)

p.9
練習8
\({\small (1)}~\{1,2,4,5\}\)
\({\small (2)}~\{1,2,4,5,6\}\)
\({\small (3)}~\{4,5\}\)
\({\small (4)}~\{1,2,4,5,6\}\)
\({\small (5)}~\{6\}\)
\({\small (6)}~\{1,2\}\)

p.10
練習9
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、

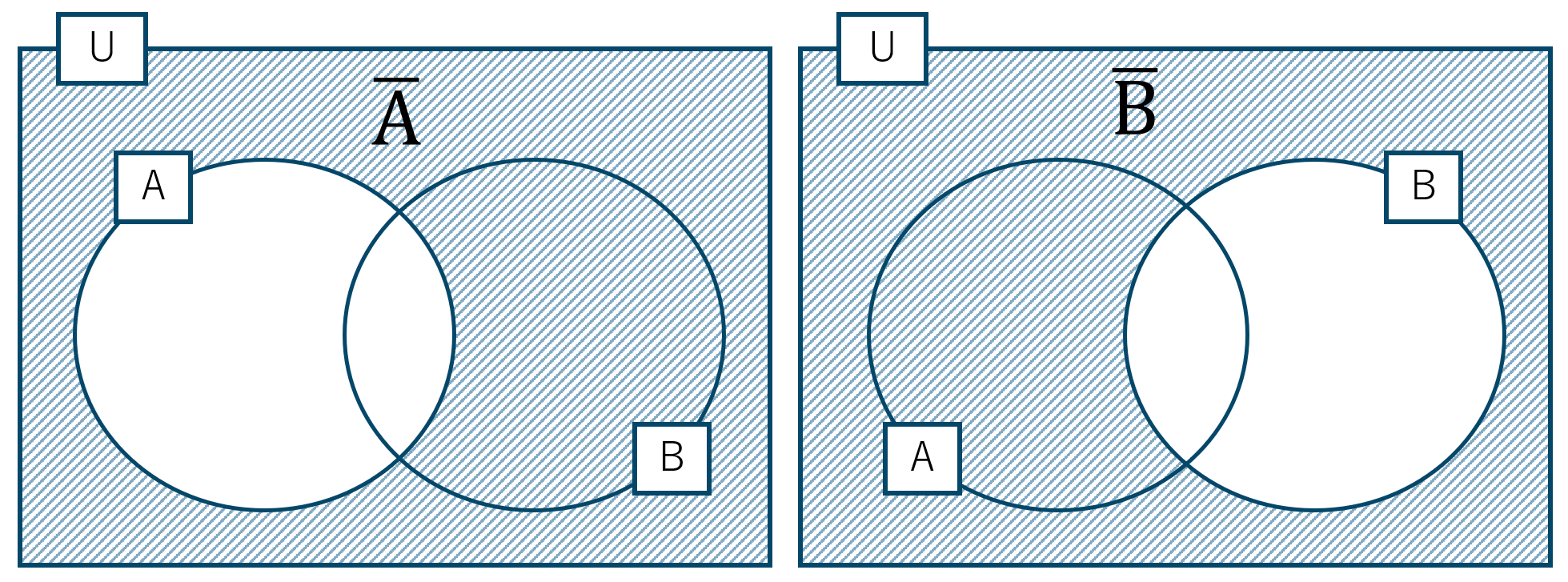
この２つの和集合となるので、

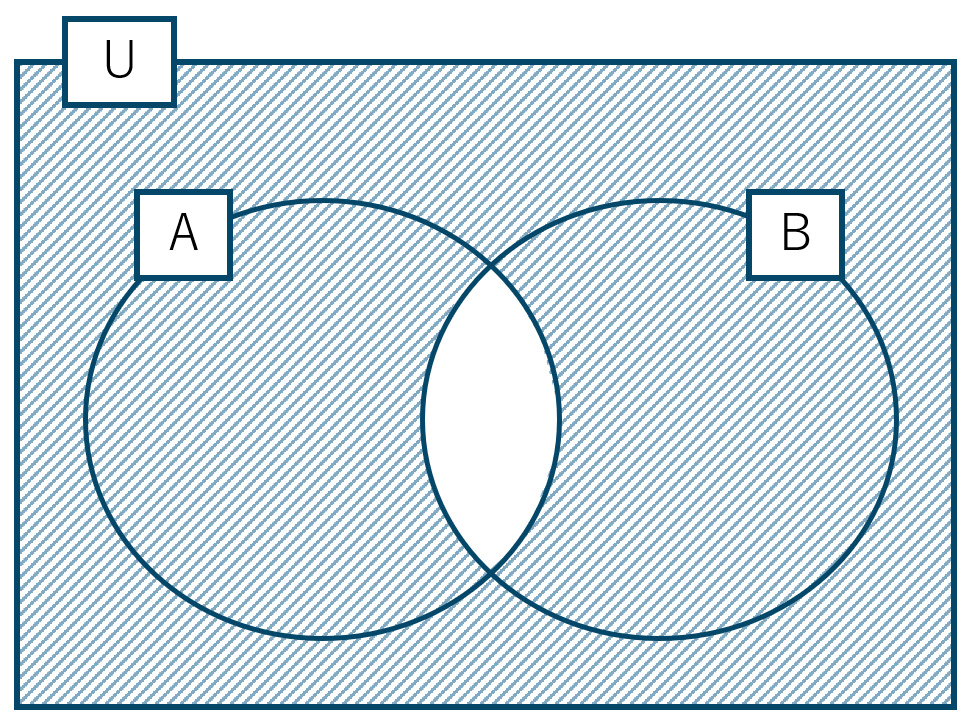
これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
　\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
→ 補集合とド・モルガンの法則

p.10
研究1
\({\rm A}\cap{\rm B}\cap{\rm C}=\{6\}\)
\({\rm A}\cup{\rm B}\cup{\rm C}=\{1,2,3,4,6,8,9,10,12\}\)

p.12
練習1
\({\small (1)}~6\)　\({\small (2)}~3\)　\({\small (3)}~2\)　\({\small (4)}~1\)　\({\small (5)}~2\)

p.13
練習2
\({\small (1)}~15\)　\({\small (2)}~3\)　\({\small (3)}~3\)

p.14
練習3
\({\small (1)}~16\)　\({\small (2)}~84\)　\({\small (3)}~8\)　\({\small (4)}~33\)

p.15
練習4
\({\small (1)}~11\)　\({\small (2)}~18\)

p.15
練習5
\({\small (1)}~16\)　\({\small (2)}~8\)
→ 集合の要素の個数
→ 補集合の要素の個数

p.16
練習6
\(\rm ABC,ACB,BAC,BCA,CAB,CBA\)

p.17
練習7
\({\small (1)}~15\)　\({\small (2)}~9\)

p.17
練習8
\(10\)

p.18
練習9
\({\small (1)}~11\)　\({\small (2)}~9\)

p.19
練習10
\({\small (1)}~36\)　\({\small (2)}~12\)
→ 和の法則と積の法則

p.19
練習11
\({\small (1)}~216\)　\({\small (2)}~12\)

p.20
練習12
\({\small (1)}~5\)　\({\small (2)}~15\)
→ 約数の個数と展開式の項の個数

p.22
練習13
\({\small (1)}~20\)　\({\small (2)}~1680\)　\({\small (3)}~3\)　\({\small (4)}~720\)
→ 順列と階乗の記号

p.22
練習14
\({\small (1)}~990\)　\({\small (2)}~840\)

p.23
練習15
\({\small (1)}~120\)　\({\small (2)}~5040\)

p.23
練習16
\(360\)

p.23
練習17
\(120\)

p.24
練習18
\({\small (1)}~14400\)　\({\small (2)}~2880\)
→ 文字の順列

p.24
練習19
\({\small (1)}~12\)　\({\small (2)}~24\)　\({\small (3)}~36\)
→ 数字の順列

p.25
練習20
\({\small (1)}~24\)　\({\small (2)}~120\)
→ 円順列とじゅず順列

p.26
練習21
\(2880\)

p.26
練習22
\(48\)
→ 条件付き円順列

p.27
練習23
\({\small (1)}~16\)　\({\small (2)}~64\)
→ 重複を許す順列

p.29
練習24
\({\small (1)}~35\)　\({\small (2)}~6\)　\({\small (3)}~8\)　\({\small (4)}~1\)

p.29
練習25
\({\small (1)}~28\)　\({\small (2)}~15\)

p.30
練習26
\({\small (1)}~5\)　\({\small (2)}~28\)　\({\small (3)}~190\)
→ 組合せの記号

p.31
練習27
\({\small (1)}~20\)　\({\small (2)}~15\)　\({\small (3)}~15\)　\({\small (4)}~9\)
→ 図形と組合せ

p.31
練習28
\(700\)
→ 代表を選ぶ

p.32
練習29
\({\small (1)}~2520\)　\({\small (2)}~105\)
→ ３つのグループに分ける

p.34
練習30
\(60\)
→ 同じものを含む順列

p.34
練習31
\({\small (1)}~10\)　\({\small (2)}~30\)　\({\small (3)}~26\)
→ 最短経路問題

p.35
研究1
\(120\)

p.36
1
\({\small (1)}~120\)　\({\small (2)}~27\)　\({\small (3)}~189\)　\({\small (4)}~9\)

p.36
2
\({\small (1)}~300\)　\({\small (2)}~144\)　\({\small (3)}~156\)

p.36
3
\({\small (1)}~140\)　\({\small (2)}~210\)
→ 代表を選ぶ

p.36
4
\({\small (1)}~560\)　\({\small (2)}~280\)
→ ３つのグループに分ける

p.39
練習32
\((1,1),(1,2),(1,3),(1,4),(1,5),(1,6)\)
\((2,1),(2,2),(2,3),(2,4),(2,5),(2,6)\)
\((3,1),(3,2),(3,3),(3,4),(3,5),(3,6)\)
\((4,1),(4,2),(4,3),(4,4),(4,5),(4,6)\)
\((5,1),(5,2),(5,3),(5,4),(5,5),(5,6)\)
\((6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\)

p.40
練習33
\({\small (1)}~{\Large \frac{1}{2}}\)　\({\small (2)}~{\Large \frac{2}{3}}\)

p.40
練習34
\({\Large \frac{2}{5}}\)
→ ボールを取り出す確率

p.40
練習35
\({\small (1)}~{\Large \frac{1}{8}}\)　\({\small (2)}~{\Large \frac{3}{8}}\)

p.41
練習36
\({\small (1)}~{\Large \frac{1}{6}}\)　\({\small (2)}~{\Large \frac{1}{4}}\)
→ さいころの確率

p.41
練習37
\({\small (1)}~{\Large \frac{1}{4}}\)　\({\small (2)}~{\Large \frac{1}{12}}\)
→ 一列に並べる確率

p.42
練習38
\({\small (1)}~{\Large \frac{1}{15}}\)　\({\small (2)}~{\Large \frac{7}{24}}\)

p.42
練習39
\({\small (1)}~{\Large \frac{10}{21}}\)　\({\small (2)}~{\Large \frac{5}{21}}\)

p.43
練習40
\({\rm A}\cup{\rm B}=\{7,9\}\)
\({\rm A}\cap{\rm B}=\{1,3,5,7,8,9,10\}\)

p.44
練習41
\({\rm A}\) と \({\rm B}\)

p.45
練習42
\({\small (1)}~{\Large \frac{3}{10}}\)　\({\small (2)}~{\Large \frac{7}{20}}\)
→ 和事象と排反事象

p.46
練習43
\({\Large \frac{11}{120}}\)

p.47
練習44
\({\Large \frac{67}{100}}\)

p.47
練習45
\({\Large \frac{13}{14}}\)

p.47
練習46
\({\Large \frac{5}{6}}\)
→ 余事象の確率

p.48
練習47
\({\small (1)}~{\Large \frac{12}{25}}\)　\({\small (2)}~{\Large \frac{13}{25}}\)
→ 和事象と排反事象

p.50
練習48
\({\small (1)}~{\Large \frac{1}{8}}\)　\({\small (2)}~{\Large \frac{1}{6}}\)

p.50
練習49
\({\small (1)}~{\Large \frac{1}{8}}\)　\({\small (2)}~{\Large \frac{7}{8}}\)

p.51
練習50
\({\small (1)}~{\Large \frac{2}{5}}\)　\({\small (2)}~{\Large \frac{8}{15}}\)
→ 独立試行の確率

p.53
練習51
\({\small (1)}~{\Large \frac{5}{324}}\)　\({\small (2)}~{\Large \frac{8}{27}}\)
→ 反復試行の確率②（さいころ）

p.53
練習52
\({\Large \frac{11}{243}}\)

p.54
練習53
\({\Large \frac{1}{2}}\)
→ 条件付き確率

p.55
練習54
\({\Large \frac{3}{5}}\)
→ 条件付き確率

p.56
練習55
\({\small (1)}~{\Large \frac{4}{15}}\)　\({\small (2)}~{\Large \frac{1}{3}}\)

p.57
練習56
\({\Large \frac{1}{286}}\)

p.57
練習57
\({\Large \frac{5}{12}}\)
→ 確率の乗法定理

p.58
5
\({\small (1)}~{\Large \frac{1}{9}}\)　\({\small (2)}~{\Large \frac{2}{9}}\)　\({\small (3)}~{\Large \frac{1}{3}}\)

p.58
6
\({\Large \frac{80}{729}}\)

p.58
7
\({\small (1)}~{\Large \frac{7}{40}}\)　\({\small (2)}~{\Large \frac{3}{10}}\)

p.59
1
\(203\)

p.59
2
\({\small (1)}~24\)　\({\small (2)}~48\)

p.59
3
\(18\)
→ 図形と組合せ

p.59
4
[証明] \(n\) 個のもののなかから \(r\) 個取り出す組合せは、\({}_{n}{\rm C}_{r}\)
\(n\) 個のもののなかに特定の \(a\) があるとき、
(ⅰ) 取り出した \(r\) 個に特定の \(a\) を含む場合
\(a\) は取り出すのが確定しているので、それ以外の \(n-1\) 個のもののなかから \(r-1\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r-1}$$(ⅱ) 取り出した \(r\) 個に特定の \(a\) を含まない場合
\(a\) 以外の \(n-1\) 個のもののなかから \(r\) 個取り出せばよいので、$$~~~{}_{n-1}{\rm C}_{r}$$これらは同時に起こらないので和の法則より、$$~~~{}_{n}{\rm C}_{r}={}_{n-1}{\rm C}_{r-1}+{}_{n-1}{\rm C}_{r}$$[終]

p.59
5
\({\small (1)}~{\Large \frac{1}{35}}\)　\({\small (2)}~{\Large \frac{5}{7}}\)

p.59
6
\({\small (1)}~{\Large \frac{5}{42}}\)　\({\small (2)}~{\Large \frac{37}{42}}\)

p.59
7
\({\Large \frac{2}{3}}\)

p.60
8
\(9\)

p.60
9
\({\small (1)}~64\)　\({\small (2)}~31\)
→ ２つのグループに分ける

p.60
10
\({\small (1)}~270\)　\({\small (2)}~210\)

p.60
11
\({\Large \frac{2}{5}}\)

p.60
12
\({\Large \frac{21}{128}}\)
→ 点が動く確率

p.60
13
\({\small (1)}~{\Large \frac{1}{3}}\)　\({\small (2)}~{\Large \frac{1}{3}}\)　\({\small (3)}~{\Large \frac{5}{27}}\)
→ ○勝先取の確率