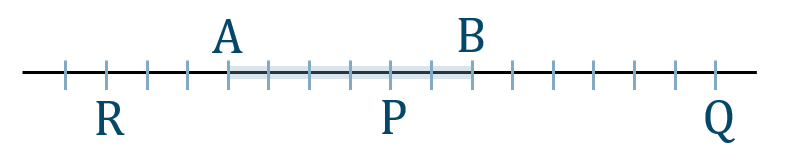文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第2章 図形の性質
第1節 平面図形
p.64
練習2
\({\small (1)}~5:3\) \({\small (2)}~{\Large \frac{15}{2}}\)
練習2
\({\small (1)}~5:3\) \({\small (2)}~{\Large \frac{15}{2}}\)
p.64
練習3
[証明]

図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\parallel EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\parallel EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
練習3
[証明]
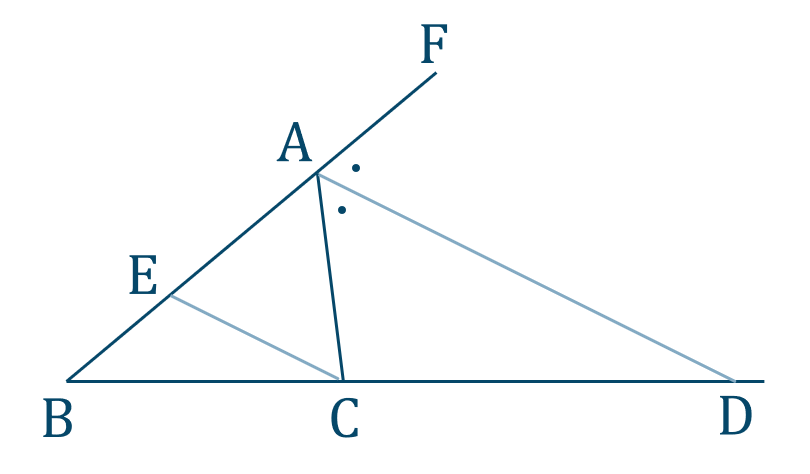
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\parallel EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\parallel EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
p.66
練習5
\({\small (1)}~40^{\circ}\) \({\small (2)}~100^{\circ}\) \({\small (3)}~20^{\circ}\)
→ 三角形の外心
練習5
\({\small (1)}~40^{\circ}\) \({\small (2)}~100^{\circ}\) \({\small (3)}~20^{\circ}\)
→ 三角形の外心
p.68
練習6
\({\small (1)}~130^{\circ}\) \({\small (2)}~25^{\circ}\) \({\small (3)}~110^{\circ}\)
→ 三角形の内心
練習6
\({\small (1)}~130^{\circ}\) \({\small (2)}~25^{\circ}\) \({\small (3)}~110^{\circ}\)
→ 三角形の内心
p.69
練習7
\({\small (1)}~5\) \({\small (2)}~4\)
練習7
\({\small (1)}~5\) \({\small (2)}~4\)
p.71
練習9
\(3:2\)
練習9
\(3:2\)
p.75
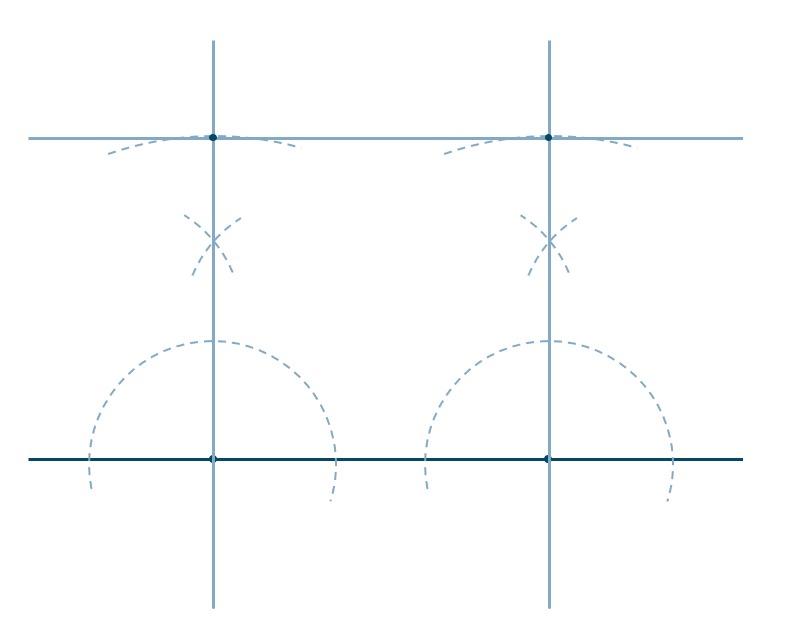
練習12
円の一部分上に任意の異なる3点 \({\rm A,B,C}\) をとります
この円の中心は三角形 \({\rm ABC}\) の外心となるります
よって、線分 \({\rm AB}\) と 線分 \({\rm BC}\) のそれぞれの垂直二等分線を引き、その交点が円の中心となります。
練習12
円の一部分上に任意の異なる3点 \({\rm A,B,C}\) をとります
この円の中心は三角形 \({\rm ABC}\) の外心となるります
よって、線分 \({\rm AB}\) と 線分 \({\rm BC}\) のそれぞれの垂直二等分線を引き、その交点が円の中心となります。
p.76
練習13
\({\small (1)}~105^{\circ}\) \({\small (2)}~60^{\circ}\) \({\small (3)}~43^{\circ}\)
→ 円周角と中心角
練習13
\({\small (1)}~105^{\circ}\) \({\small (2)}~60^{\circ}\) \({\small (3)}~43^{\circ}\)
→ 円周角と中心角
p.76
練習14
\({\small (1)}\)
対頂角より、
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)
\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
練習14
\({\small (1)}\)
対頂角より、
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)
\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
p.78
練習16
②、③
練習16
②、③
p.81
練習18
\({\small (1)}~60^{\circ}\) \({\small (2)}~78^{\circ}\) \({\small (3)}~85^{\circ}\)
→ 接弦定理
練習18
\({\small (1)}~60^{\circ}\) \({\small (2)}~78^{\circ}\) \({\small (3)}~85^{\circ}\)
→ 接弦定理
p.83
練習20
[証明]方べきの定理より、
\({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\)
ここで、\({\rm PC}=r+{\rm PO},{\rm PF}=r-{\rm PO}\) であることより、
\({\rm PA}\cdot{\rm PB}=(r+{\rm PO})(r-{\rm PO})\)
したがって、
\({\rm PA}\cdot{\rm PB}=r^2-{\rm PO}^2\) [終]
練習20
[証明]方べきの定理より、
\({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\)
ここで、\({\rm PC}=r+{\rm PO},{\rm PF}=r-{\rm PO}\) であることより、
\({\rm PA}\cdot{\rm PB}=(r+{\rm PO})(r-{\rm PO})\)
したがって、
\({\rm PA}\cdot{\rm PB}=r^2-{\rm PO}^2\) [終]
p.83
練習21
[証明]

\(\triangle{\rm PAT}\) と \(\triangle{\rm PTB}\) において、
共通の角より、\(\angle{\rm APT}=\angle{\rm TPB}\)
接弦定理より、\(\angle{\rm PAT}=\angle{\rm PBT}\)
よって、2組の角がそれぞれ等しいので
\(\triangle{\rm PAT}\sim\triangle{\rm PTB}\)
対応する辺の比が等しいので、
\({\rm PA}:{\rm PT}={\rm PT}:{\rm PB}\)
計算すると、
\({\rm PA}\cdot{\rm PB}={\rm PT}^2\) [終]
練習21
[証明]
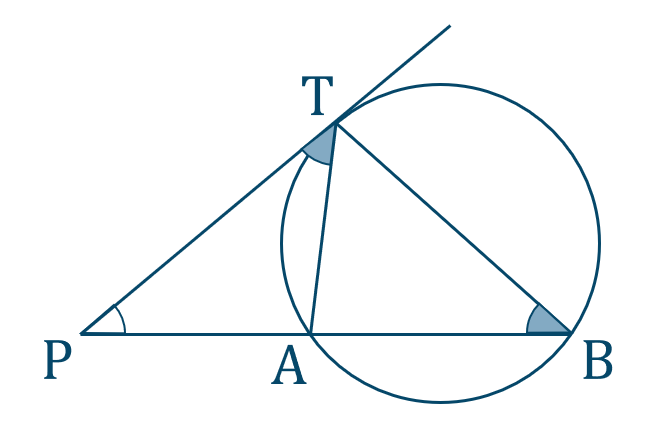
\(\triangle{\rm PAT}\) と \(\triangle{\rm PTB}\) において、
共通の角より、\(\angle{\rm APT}=\angle{\rm TPB}\)
接弦定理より、\(\angle{\rm PAT}=\angle{\rm PBT}\)
よって、2組の角がそれぞれ等しいので
\(\triangle{\rm PAT}\sim\triangle{\rm PTB}\)
対応する辺の比が等しいので、
\({\rm PA}:{\rm PT}={\rm PT}:{\rm PB}\)
計算すると、
\({\rm PA}\cdot{\rm PB}={\rm PT}^2\) [終]
p.84
\({\small (2)}~d=r+r’\) \({\small (3)}~r-r’ < d < r+r’\)
\({\small (4)}~d=r-r’\) \({\small (5)}~d < r-r’\)
→ 2つの円の位置関係と共通接線
\({\small (2)}~d=r+r’\) \({\small (3)}~r-r’ < d < r+r’\)
\({\small (4)}~d=r-r’\) \({\small (5)}~d < r-r’\)
→ 2つの円の位置関係と共通接線
p.85
練習22
\({\small (1)}~\)[2] \({\small (2)}~\)[1]
\({\small (3)}~\)[4] \({\small (4)}~\)[3]
\({\small (5)}~\)[5]
→ 2つの円の位置関係と共通接線
練習22
\({\small (1)}~\)[2] \({\small (2)}~\)[1]
\({\small (3)}~\)[4] \({\small (4)}~\)[3]
\({\small (5)}~\)[5]
→ 2つの円の位置関係と共通接線
p.86
練習23
\(2\sqrt{6}\)
練習23
\(2\sqrt{6}\)
p.88
練習26
四角形 \(\rm ABCP\) は4つの辺が等しいのでひし形となる
したがって、直線 \(\rm PC\) は直線 \(l\) と平行となる
練習26
四角形 \(\rm ABCP\) は4つの辺が等しいのでひし形となる
したがって、直線 \(\rm PC\) は直線 \(l\) と平行となる
補充問題
p.91
1
[証明]

点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
\({\rm CB\parallel QR,CA\parallel PR,AB\parallel QP}\)
ここで、\({\rm CB\parallel QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
1
[証明]
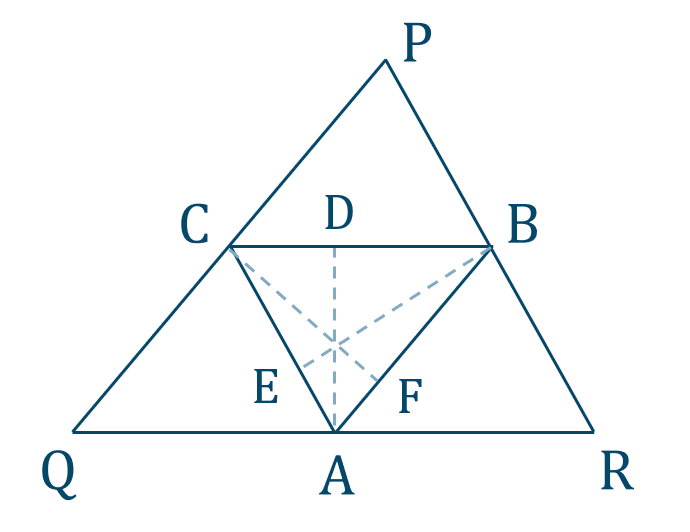
点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
\({\rm CB\parallel QR,CA\parallel PR,AB\parallel QP}\)
ここで、\({\rm CB\parallel QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
p.91
2
[証明]

点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
2
[証明]
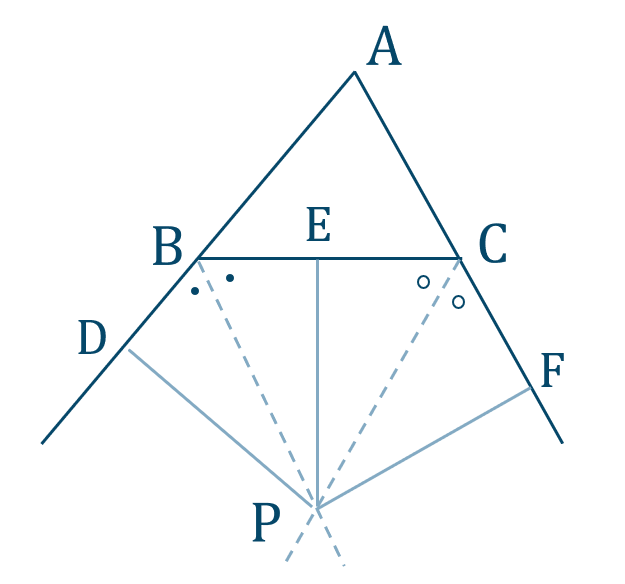
点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
p.91
3
[証明]

\(\triangle{\rm PAD}\) と \(\triangle{\rm PCB}\) において、
条件の \({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\) より比の式にすると、
\({\rm PA}:{\rm PD}={\rm PC}:{\rm PB}\)
また、対頂角より、(右の図では共通の角)
\(\angle{\rm APD}=\angle{\rm CPB}\)
よって、2組の角がそれぞれ等しいので
\(\triangle{\rm PAD}\sim\triangle{\rm PCB}\)
対応する角が等しいので、
\(\angle{\rm PDA}=\angle{\rm PBC}\)
また、
\(\angle{\rm CDA}=\angle{\rm ABC}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある[終]
3
[証明]

\(\triangle{\rm PAD}\) と \(\triangle{\rm PCB}\) において、
条件の \({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\) より比の式にすると、
\({\rm PA}:{\rm PD}={\rm PC}:{\rm PB}\)
また、対頂角より、(右の図では共通の角)
\(\angle{\rm APD}=\angle{\rm CPB}\)
よって、2組の角がそれぞれ等しいので
\(\triangle{\rm PAD}\sim\triangle{\rm PCB}\)
対応する角が等しいので、
\(\angle{\rm PDA}=\angle{\rm PBC}\)
また、
\(\angle{\rm CDA}=\angle{\rm ABC}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある[終]
第2節 空間図形
p.93
練習30
\({\small (1)}~\)辺CD、辺EF、辺GH
\({\small (2)}~\)辺FG、辺EH、辺CG、辺DH
\({\small (3)}~{\large ①}~90^{\circ}\) \({\large ②}~45^{\circ}\) \({\large ③}~90^{\circ}\)
→ 空間図形の位置関係
練習30
\({\small (1)}~\)辺CD、辺EF、辺GH
\({\small (2)}~\)辺FG、辺EH、辺CG、辺DH
\({\small (3)}~{\large ①}~90^{\circ}\) \({\large ②}~45^{\circ}\) \({\large ③}~90^{\circ}\)
→ 空間図形の位置関係
p.93
練習31
\({\small (1)}~\)[証明]
条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である[終]
\({\small (2)}~\)[証明]
(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
練習31
\({\small (1)}~\)[証明]
条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である[終]
\({\small (2)}~\)[証明]
(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
p.95
練習32
\({\small (1)}~\)

図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \parallel \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)

図より、\({\rm \alpha \parallel l , \beta \parallel l}\) としても \({\rm \alpha \parallel \beta}\) でない
よって、正しくない
練習32
\({\small (1)}~\)
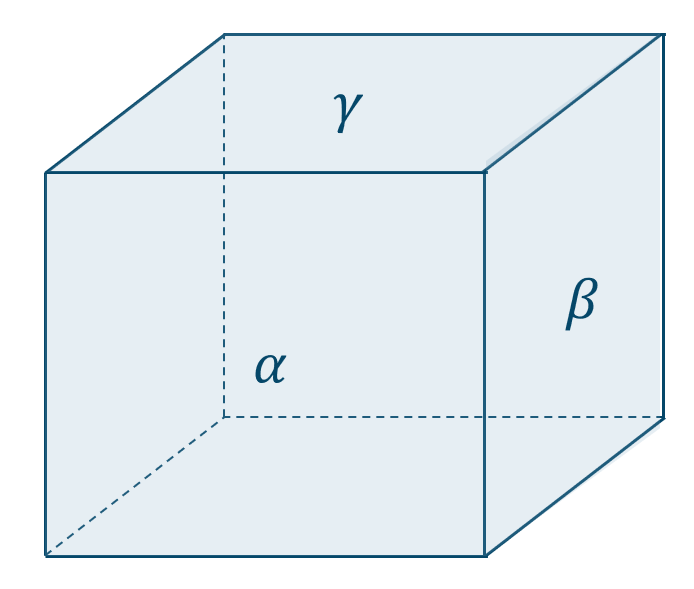
図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \parallel \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)
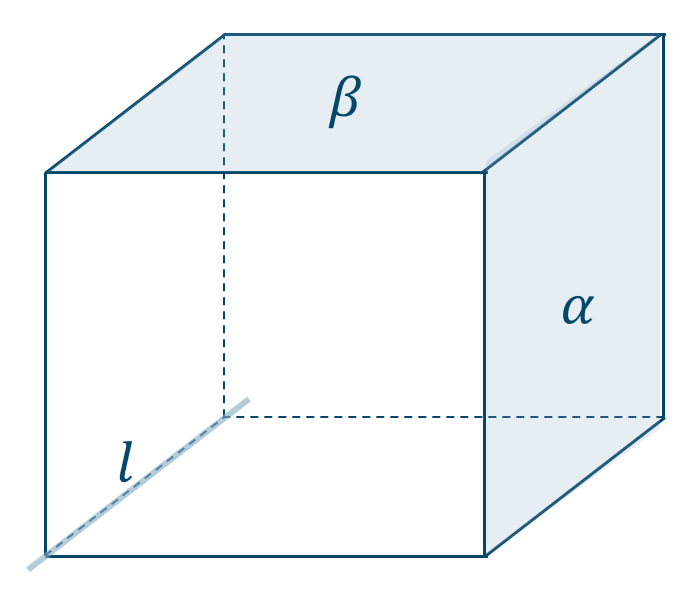
図より、\({\rm \alpha \parallel l , \beta \parallel l}\) としても \({\rm \alpha \parallel \beta}\) でない
よって、正しくない
p.96
研究1
\({\small (1)}~\)[証明]
\(\rm EA \perp \) 面 \(\rm EFGH\)
\(\rm EK \perp FH\)
よって、三垂線の定理1より
\(\rm AK \perp FH\) [終]
\({\small (2)}~\)[証明] \(\rm AE \perp \) 面 \(\rm ABCD\) より、
\(\rm BD \perp AE\)
正方形 \(\rm ABCD\) の対角線は直交するので、
\(\rm BD \perp AC\)
これらより、\(\rm BD \perp \) 面 \(\rm ACE\) となり、点 \(\rm G\) が面 \(\rm ACE\) 上にあるので、
\(\rm AG \perp BD\) [終]
研究1
\({\small (1)}~\)[証明]
\(\rm EA \perp \) 面 \(\rm EFGH\)
\(\rm EK \perp FH\)
よって、三垂線の定理1より
\(\rm AK \perp FH\) [終]
\({\small (2)}~\)[証明] \(\rm AE \perp \) 面 \(\rm ABCD\) より、
\(\rm BD \perp AE\)
正方形 \(\rm ABCD\) の対角線は直交するので、
\(\rm BD \perp AC\)
これらより、\(\rm BD \perp \) 面 \(\rm ACE\) となり、点 \(\rm G\) が面 \(\rm ACE\) 上にあるので、
\(\rm AG \perp BD\) [終]
p.98
練習33
正四面体 \(4\) 正三角形 \(4\) \(6\)
正六面体 \(6\) 正方形 \(8\) \(12\)
正十二面体 \(12\) 正五角形 \(20\) \(30\)
正二十面体 \(20\) 正三角形 \(12\) \(30\)
練習33
正四面体 \(4\) 正三角形 \(4\) \(6\)
正六面体 \(6\) 正方形 \(8\) \(12\)
正十二面体 \(12\) 正五角形 \(20\) \(30\)
正二十面体 \(20\) 正三角形 \(12\) \(30\)
p.98
練習34
それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
練習34
それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
p.98
練習35
面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\(14-24+12=2\)
練習35
面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\(14-24+12=2\)
p.99
練習36
\({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である
練習36
\({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である
p.100
研究1
\({\Large \frac{\sqrt{2}}{12}}a^3\)
研究1
\({\Large \frac{\sqrt{2}}{12}}a^3\)
補充問題
p.102
4
\({\small (1)}~\)

図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
4
\({\small (1)}~\)
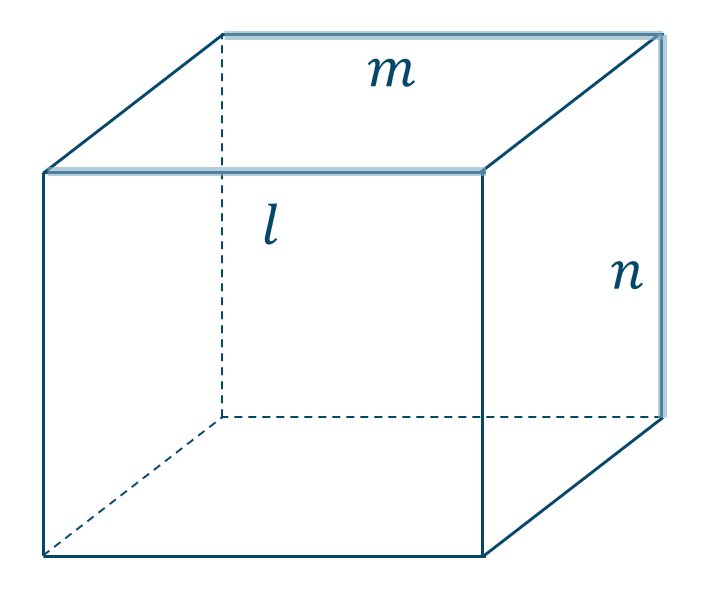
図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
p.102
5
頂点 \(60\)、辺 \(90\)
5
頂点 \(60\)、辺 \(90\)
章末問題 図形の性質
章末問題A
p.103
1
\({\small (1)}~{\Large \frac{20}{7}}\) \({\small (2)}~7:5\)
1
\({\small (1)}~{\Large \frac{20}{7}}\) \({\small (2)}~7:5\)
p.103
2
\({\small (1)}~125^{\circ}\) \({\small (2)}~52^{\circ}\)
2
\({\small (1)}~125^{\circ}\) \({\small (2)}~52^{\circ}\)
p.103
3
\({\small (1)}~45^{\circ}\) \({\small (2)}~2\)
3
\({\small (1)}~45^{\circ}\) \({\small (2)}~2\)
p.103
4
\({\small (1)}~1:1\) \({\small (2)}~3:5\)
4
\({\small (1)}~1:1\) \({\small (2)}~3:5\)
p.103
5
[証明]

\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \parallel AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \parallel AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \parallel SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる
5
[証明]
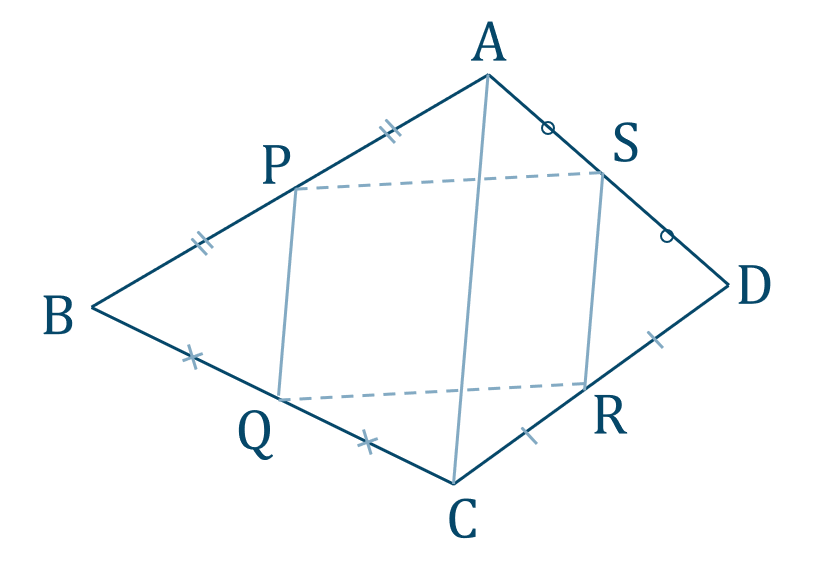
\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \parallel AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \parallel AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \parallel SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる
章末問題B
p.104
6
[証明]

点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
6
[証明]
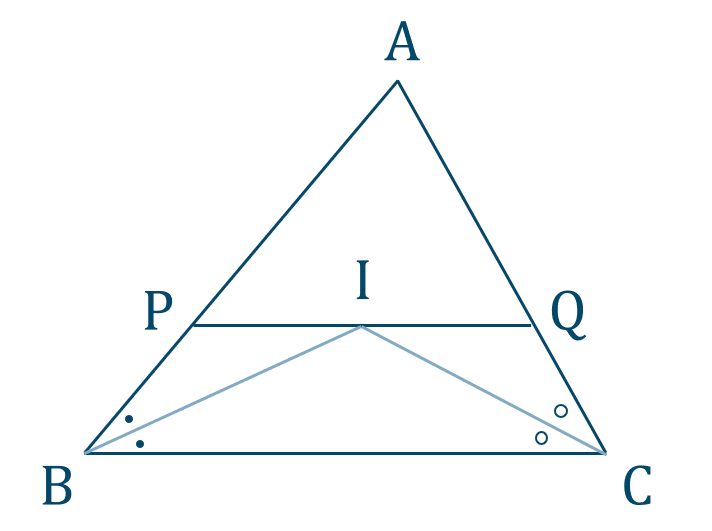
点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
p.104
7
[証明]

\({\rm AD \parallel BC}\) より、錯角との関係を用いて、
\(\angle{\rm BAD}+\angle{\rm ABC}=180^{\circ}\)
また、四角形 \(\rm APQB\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm PAD}+\angle{\rm DQP}=180^{\circ}\)
ここで、\(\angle{\rm BAD}=\angle{\rm PAD}\) であるので、
\(\angle{\rm ABC}=\angle{\rm DQP}\)
これより、四角形 \(\rm PBCQ\) において、内角と対角の外角が等しくなる
したがって、四角形 \(\rm PBCQ\) は円に内接する[終]
7
[証明]
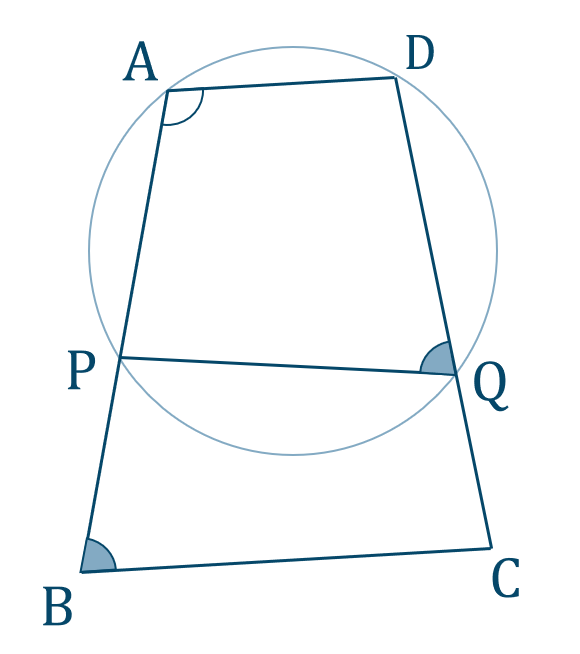
\({\rm AD \parallel BC}\) より、錯角との関係を用いて、
\(\angle{\rm BAD}+\angle{\rm ABC}=180^{\circ}\)
また、四角形 \(\rm APQB\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm PAD}+\angle{\rm DQP}=180^{\circ}\)
ここで、\(\angle{\rm BAD}=\angle{\rm PAD}\) であるので、
\(\angle{\rm ABC}=\angle{\rm DQP}\)
これより、四角形 \(\rm PBCQ\) において、内角と対角の外角が等しくなる
したがって、四角形 \(\rm PBCQ\) は円に内接する[終]
p.104
8
[証明]

\(\angle{\rm ACB}=x\) とすると、円周角と中心角の関係より、
\(\angle{\rm AOB}=2\angle{\rm ACB}=2x\)
また、四角形 \(\rm AOBD\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm ADB}=180^{\circ}-\angle{\rm AOB}=180^{\circ}-2x\)
次に \(\triangle{\rm DCB}\) の内角の和より、
\(\angle{\rm DBC}=180^{\circ}-(\angle{\rm DCB}+\angle{\rm CDB})\)
\(~~~~~=180^{\circ}-(x+180^{\circ}-2x)=x\)
よって、\(\angle{\rm DCB}=\angle{\rm DBC}=x\) となるので、\(\triangle{\rm DCB}\) は二等辺三角形となる[終]
8
[証明]
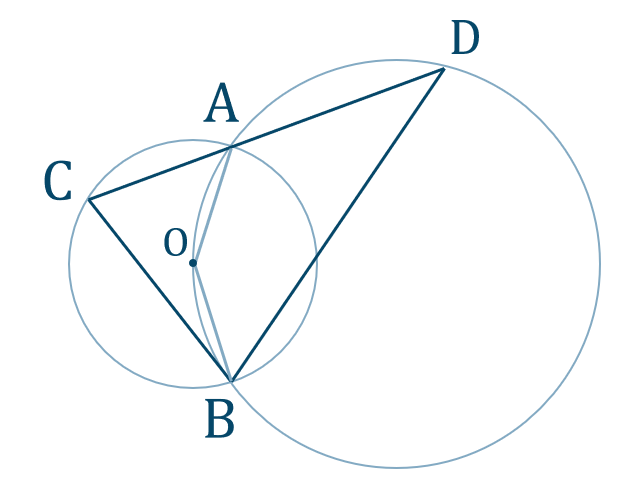
\(\angle{\rm ACB}=x\) とすると、円周角と中心角の関係より、
\(\angle{\rm AOB}=2\angle{\rm ACB}=2x\)
また、四角形 \(\rm AOBD\) は円に内接するので、対角の和が \(180^{\circ}\) より、
\(\angle{\rm ADB}=180^{\circ}-\angle{\rm AOB}=180^{\circ}-2x\)
次に \(\triangle{\rm DCB}\) の内角の和より、
\(\angle{\rm DBC}=180^{\circ}-(\angle{\rm DCB}+\angle{\rm CDB})\)
\(~~~~~=180^{\circ}-(x+180^{\circ}-2x)=x\)
よって、\(\angle{\rm DCB}=\angle{\rm DBC}=x\) となるので、\(\triangle{\rm DCB}\) は二等辺三角形となる[終]
p.104
9
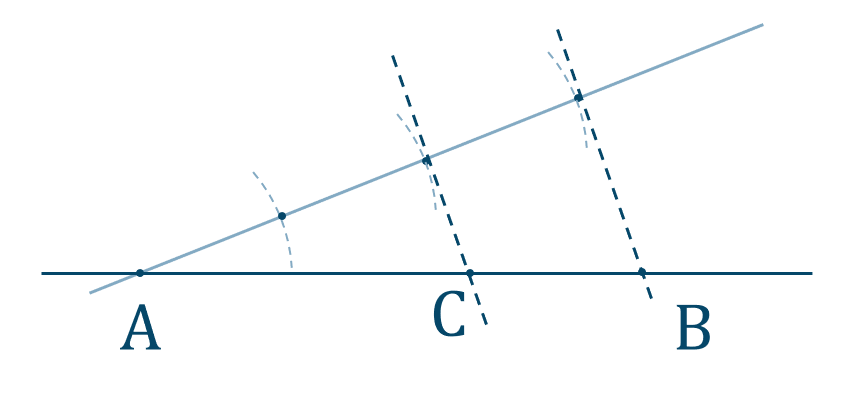
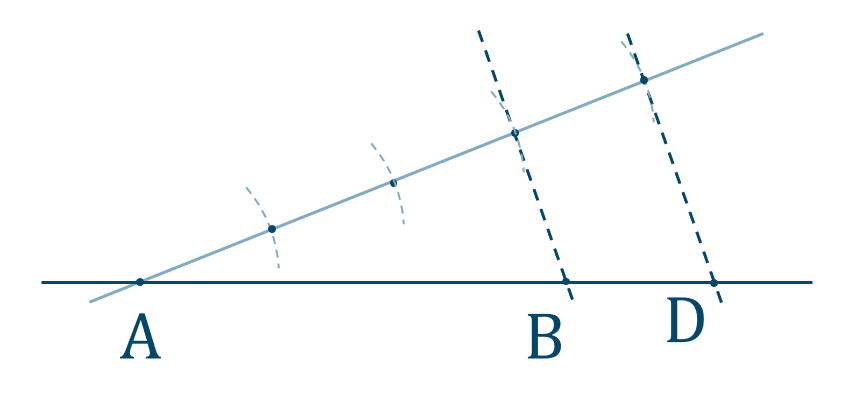
\({\small (1)}~\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、

これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
9
\({\small (1)}~\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、
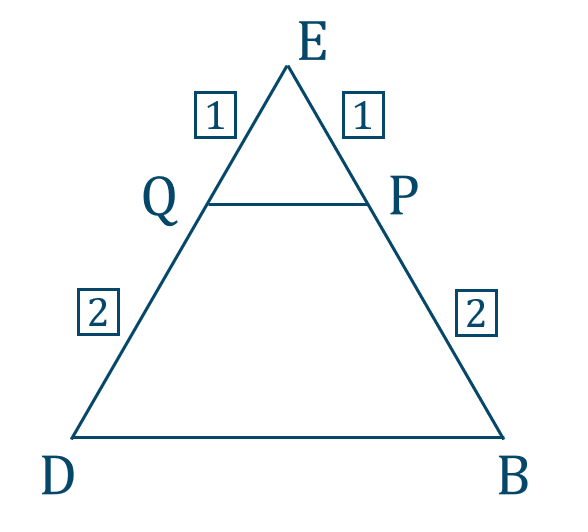
これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
次のページ「第3章 整数の性質」