このページは、東京書籍:Advanced数学A[701]
2章 図形の性質
2章 図形の性質

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学A 1章 場合の数と確率
Advanced数学A 2章 図形の性質
Advanced数学A 3章 数学の人間の活動
2章 図形の性質
1節 三角形の性質
p.66 問1$$~~~7$$→ 中点連結定理と平行線と比
p.68 問3$$~~~{\rm AG}=4~,~{\rm GQ}=2$$→ 三角形の重心
p.69 問4$$~~~140^\circ$$→ 三角形の外心
p.69 問5 \({\rm BC}\) の中点
p.71 問7[証明] \(\triangle {\rm ABC}\) の外心と垂心が点 \({\rm O}\) で一致したとする
また、辺 \({\rm BC}\) の中点を \({\rm D}\) とする

点 \({\rm O}\) は外心より、直線 \({\rm OD}\) は垂直二等分線である
また、点 \({\rm O}\) は垂心てあり、\({\rm AD}\) は垂線であるので \({\rm A~,~O~,~D}\) は一直線上にある
これより、点 \({\rm A}\) は辺 \({\rm BC}\) の垂直二等分線であるから
\({\rm AB=AC}\)
同様に考えて、
\({\rm BC=AC}\)
したがって、\(\triangle {\rm ABC}\) は3辺の長さが等しく、正三角形である [終]
また、辺 \({\rm BC}\) の中点を \({\rm D}\) とする

点 \({\rm O}\) は外心より、直線 \({\rm OD}\) は垂直二等分線である
また、点 \({\rm O}\) は垂心てあり、\({\rm AD}\) は垂線であるので \({\rm A~,~O~,~D}\) は一直線上にある
これより、点 \({\rm A}\) は辺 \({\rm BC}\) の垂直二等分線であるから
\({\rm AB=AC}\)
同様に考えて、
\({\rm BC=AC}\)
したがって、\(\triangle {\rm ABC}\) は3辺の長さが等しく、正三角形である [終]
p.72 問8$$~~~{ \frac{\,7\,}{\,2\,}}$$→ 角の二等分線と比
p.72 問9[証明] \(\triangle {\rm ABM}\) について、\(\angle {\rm AMB}\) の角の二等分線と比の関係より、
\(\rm AD:DB=AM:MB\)
次に \(\triangle {\rm AMC}\) について、\(\angle {\rm AMC}\) の角の二等分線と比の関係より、
\(\rm AE:EC=AM:MC\)
また、点 \(\rm M\) は中点より、\(MB=MC\)
以上より、
\(\rm AD:DB=AE:EC\)
したがって、\(\triangle {\rm ABC}\) について、三角形の平行線と比の関係より、
\(DE\,//\, BC\) [終]
\(\rm AD:DB=AM:MB\)
次に \(\triangle {\rm AMC}\) について、\(\angle {\rm AMC}\) の角の二等分線と比の関係より、
\(\rm AE:EC=AM:MC\)
また、点 \(\rm M\) は中点より、\(MB=MC\)
以上より、
\(\rm AD:DB=AE:EC\)
したがって、\(\triangle {\rm ABC}\) について、三角形の平行線と比の関係より、
\(DE\,//\, BC\) [終]
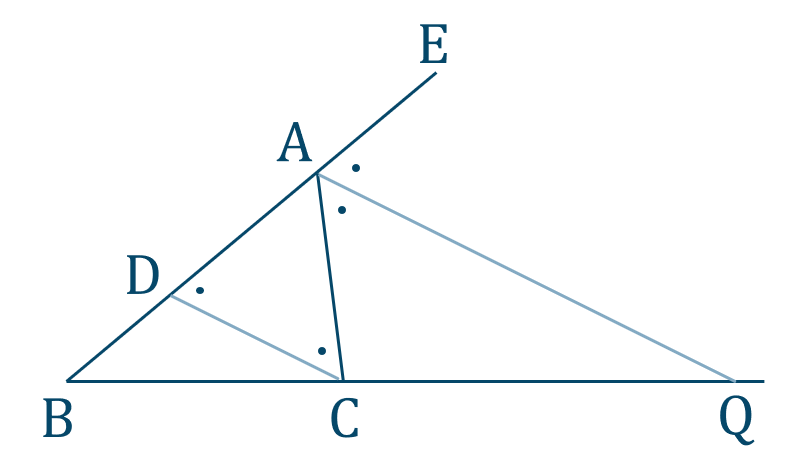
p.73 問10[証明]

図のように、\({\rm AB}\) の延長線上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm EAQ}=\angle{\rm CAQ}\) …①
同位角より、
\(\angle{\rm EAQ}=\angle{\rm ADC}\) …②
錯角より、
\(\angle{\rm CAQ}=\angle{\rm ACD}\) …③
①、②、③より
\(\angle{\rm ADC}=\angle{\rm ACD}\)
よって、\(\triangle{\rm ADC}\) は \({\rm AD=AC}\) の二等辺三角形となる
また、\({\rm AQ\,//\, DC}\) の平行線と線分の比より
\({\rm BQ}:{\rm CQ}={\rm BA}:{\rm DA}\)
\({\rm AD=AC}\) とすると、
\({\rm BQ}:{\rm QC}={\rm AB}:{\rm AC}\) [終]
図のように、\({\rm AB}\) の延長線上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm EAQ}=\angle{\rm CAQ}\) …①
同位角より、
\(\angle{\rm EAQ}=\angle{\rm ADC}\) …②
錯角より、
\(\angle{\rm CAQ}=\angle{\rm ACD}\) …③
①、②、③より
\(\angle{\rm ADC}=\angle{\rm ACD}\)
よって、\(\triangle{\rm ADC}\) は \({\rm AD=AC}\) の二等辺三角形となる
また、\({\rm AQ\,//\, DC}\) の平行線と線分の比より
\({\rm BQ}:{\rm CQ}={\rm BA}:{\rm DA}\)
\({\rm AD=AC}\) とすると、
\({\rm BQ}:{\rm QC}={\rm AB}:{\rm AC}\) [終]
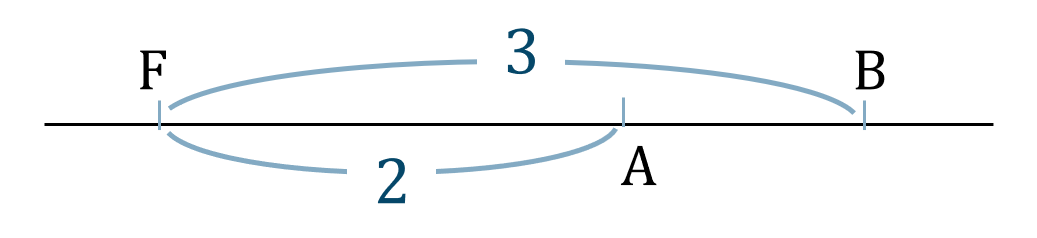
p.73 問11$$~~~10$$→ 角の二等分線と比
p.74 問12$$~~~125^\circ$$→ 三角形の内心
p.75 参考 問1[証明] \(\angle{\rm A}~,~ \angle{\rm B}~,~ \angle{\rm C}\) に対する傍心がそれぞれ \({\rm J~,~J’~,~J”}\) であるとき、
\({\rm AJ~,~BJ’~,~CJ”}\) はそれぞれの角の二等分線であるので、その交点は \(\triangle {\rm ABC}\) の内心 \({\rm I}\) と一致する
また、\({\rm AJ’~,~AJ”}\) はともに \(\angle {\rm A}\) の外角の二等分線であるので、
\(\angle{\rm J’AC}=\angle{\rm J”AB}=a\)
また、\({\rm AJ}\) は内角の二等分線より
\(\angle{\rm CAJ}=\angle{\rm BAJ}=b\)
よって、\(a+a+b+b=180^\circ\) で \(a+b=90^\circ\) となるので、
\(\angle{\rm JAJ’}=\angle{\rm JAJ”}=90^\circ\)
よって、\({\rm AJ}\) と \({\rm J’J”}\) は垂直である
同様に考えて、\({\rm BJ’}\) と \({\rm JJ”}\) は垂直であり、\({\rm CJ”}\) と \({\rm JJ’}\) は垂直である
これより、内心 \({\rm I}\) は \(\triangle {\rm JJ’J”}\) の垂心でもある
したがって、
\(\triangle {\rm JJ’J”}\) の垂心と \(\triangle {\rm ABC}\) の内心は一致する [終]
\({\rm AJ~,~BJ’~,~CJ”}\) はそれぞれの角の二等分線であるので、その交点は \(\triangle {\rm ABC}\) の内心 \({\rm I}\) と一致する
また、\({\rm AJ’~,~AJ”}\) はともに \(\angle {\rm A}\) の外角の二等分線であるので、
\(\angle{\rm J’AC}=\angle{\rm J”AB}=a\)
また、\({\rm AJ}\) は内角の二等分線より
\(\angle{\rm CAJ}=\angle{\rm BAJ}=b\)
よって、\(a+a+b+b=180^\circ\) で \(a+b=90^\circ\) となるので、
\(\angle{\rm JAJ’}=\angle{\rm JAJ”}=90^\circ\)
よって、\({\rm AJ}\) と \({\rm J’J”}\) は垂直である
同様に考えて、\({\rm BJ’}\) と \({\rm JJ”}\) は垂直であり、\({\rm CJ”}\) と \({\rm JJ’}\) は垂直である
これより、内心 \({\rm I}\) は \(\triangle {\rm JJ’J”}\) の垂心でもある
したがって、
\(\triangle {\rm JJ’J”}\) の垂心と \(\triangle {\rm ABC}\) の内心は一致する [終]
p.76 問13[証明]

頂点 \({\rm C}\) を通り、直線 \(l\) に平行な直線を引き、直線 \({\rm AB}\) との交点を \({\rm D}\) とすると、
\({\rm PR\,//\,CD~,~CD\,//\,QR}\) より、$$~~~{\rm \frac{\,BD\,}{\,PC\,}=\frac{\,BR\,}{\,RD\,}~,~\frac{\,CQ\,}{\,QA\,}=\frac{\,DR\,}{\,RA\,}}$$これより、$$\scriptsize~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}\cdot\frac{\,AR\,}{\,RB\,}=\frac{\,BR\,}{\,RD\,}\cdot\frac{\,DR\,}{\,RA\,}\cdot\frac{\,AR\,}{\,RB\,}=1}$$したがって、$$~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}\cdot\frac{\,AR\,}{\,RB\,}=1}$$[終]
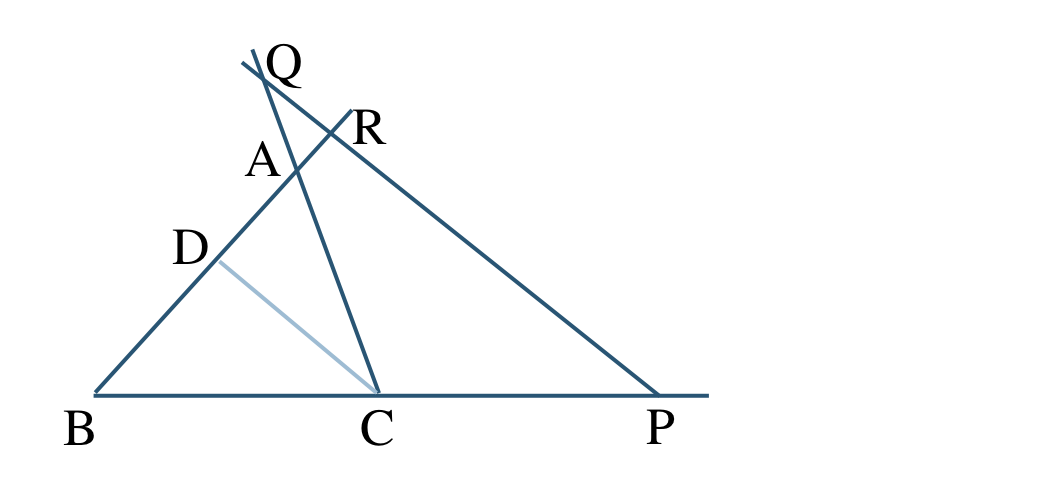
頂点 \({\rm C}\) を通り、直線 \(l\) に平行な直線を引き、直線 \({\rm AB}\) との交点を \({\rm D}\) とすると、
\({\rm PR\,//\,CD~,~CD\,//\,QR}\) より、$$~~~{\rm \frac{\,BD\,}{\,PC\,}=\frac{\,BR\,}{\,RD\,}~,~\frac{\,CQ\,}{\,QA\,}=\frac{\,DR\,}{\,RA\,}}$$これより、$$\scriptsize~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}\cdot\frac{\,AR\,}{\,RB\,}=\frac{\,BR\,}{\,RD\,}\cdot\frac{\,DR\,}{\,RA\,}\cdot\frac{\,AR\,}{\,RB\,}=1}$$したがって、$$~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}\cdot\frac{\,AR\,}{\,RB\,}=1}$$[終]
p.76 問14$${\small (1)}~2$$$${\small (2)}~9$$→ メネラウスの定理
p.77 問15[証明] \(\triangle {\rm BRC}\) について、メネラウスの定理より、$$~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CS\,}{\,SR\,}\cdot\frac{\,RA\,}{\,AB\,}}=1~~~\cdots{\large ①}$$\(\triangle {\rm ARC}\) について、メネラウスの定理より、$$~~~{\rm \frac{\,AB\,}{\,BR\,}\cdot\frac{\,RS\,}{\,SC\,}\cdot\frac{\,CQ\,}{\,QA\,}}=1~~~\cdots{\large ②}$$①と②より、両辺を掛け算すると、$$\scriptsize~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CS\,}{\,SR\,}\cdot\frac{\,RA\,}{\,AB\,}}\cdot{\rm \frac{\,AB\,}{\,BR\,}\cdot\frac{\,RS\,}{\,SC\,}\cdot\frac{\,CQ\,}{\,QA\,}}=1$$$$~~~{\rm \frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}\cdot\frac{\,AR\,}{\,RB\,}}=1$$[終]
p.78 問16$${\small (1)}~4$$$${\small (2)}~5$$→ チェバの定理
p.78 問17[証明]
\(\triangle {\rm ABC}\) について、チェバの定理より、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{BM}{MC}}\cdot{ \frac{CQ}{QA}}=1}$$ここで、\({\rm BM=MC}\) より、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{1}{1}}\cdot{ \frac{CQ}{QA}}=1}$$よって、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{CQ}{QA}}=1}$$計算すると、
\({\rm AP:PB=AQ:QC}\)
したがって、平行線と比の関係より、
\({\rm PQ\,//\, BC}\) [終]
\(\triangle {\rm ABC}\) について、チェバの定理より、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{BM}{MC}}\cdot{ \frac{CQ}{QA}}=1}$$ここで、\({\rm BM=MC}\) より、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{1}{1}}\cdot{ \frac{CQ}{QA}}=1}$$よって、$$~~~{\rm { \frac{AP}{PB}}\cdot{ \frac{CQ}{QA}}=1}$$計算すると、
\({\rm AP:PB=AQ:QC}\)
したがって、平行線と比の関係より、
\({\rm PQ\,//\, BC}\) [終]
p.79 参考 問1\({\small (1)}~\)[証明]

\({\rm BC~,~AC~,~AB}\) の中点 \({\rm P~,~Q~,~R}\) とすると、$$~~~{\rm \frac{\,AR\,}{\,RB\,}}=1~,~{\rm \frac{\,BP\,}{\,PC\,}}=1~,~{\rm \frac{\,CQ\,}{\,QA\,}}=1$$これより、$$~~~{\rm \frac{\,AR\,}{\,RB\,}}\cdot{\rm \frac{\,BP\,}{\,PC\,}}\cdot{\rm \frac{\,CQ\,}{\,QA\,}}=1$$チェバの定理の逆が成り立つことより、3本の中線 \({\rm AP~,~BQ~,~CR}\) は1点で交わる [終]
\({\small (2)}~\)[証明]

角の二等分線との交点を \({\rm P~,~Q~,~R}\) にすると、角の二等分線の比の関係より、$$\scriptsize~~~{\rm \frac{\,AR\,}{\,RB\,}=\frac{\,CA\,}{\,CB\,}~,~\frac{\,BP\,}{\,PC\,}=\frac{\,AB\,}{\,AC\,}~,~\frac{\,CQ\,}{\,QA\,}=\frac{\,BC\,}{\,BA\,}}$$これより、$$\scriptsize~~~{\rm \frac{\,AR\,}{\,RB\,}\cdot\frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}=\frac{\,CA\,}{\,CB\,}\cdot\frac{\,AB\,}{\,AC\,}\cdot\frac{\,BC\,}{\,BA\,}=1}$$チェバの定理の逆が成り立つことより、3つの内角の二等分線は1点で交わる [終]
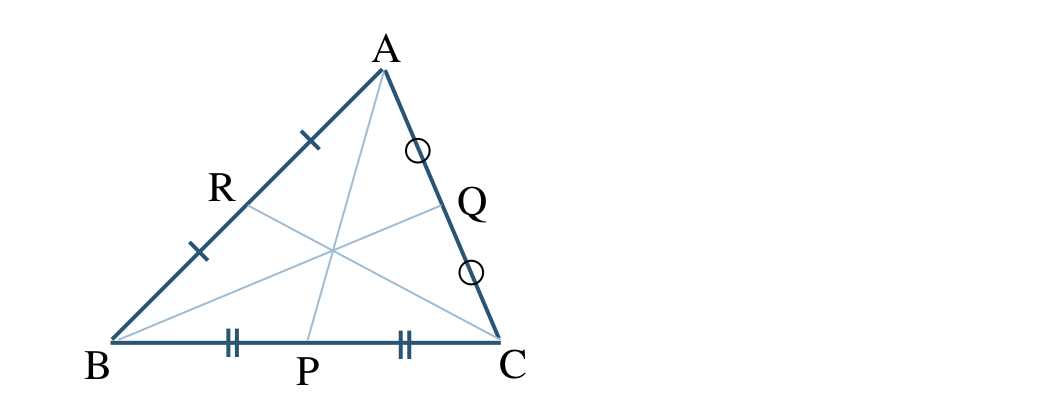
\({\rm BC~,~AC~,~AB}\) の中点 \({\rm P~,~Q~,~R}\) とすると、$$~~~{\rm \frac{\,AR\,}{\,RB\,}}=1~,~{\rm \frac{\,BP\,}{\,PC\,}}=1~,~{\rm \frac{\,CQ\,}{\,QA\,}}=1$$これより、$$~~~{\rm \frac{\,AR\,}{\,RB\,}}\cdot{\rm \frac{\,BP\,}{\,PC\,}}\cdot{\rm \frac{\,CQ\,}{\,QA\,}}=1$$チェバの定理の逆が成り立つことより、3本の中線 \({\rm AP~,~BQ~,~CR}\) は1点で交わる [終]
\({\small (2)}~\)[証明]
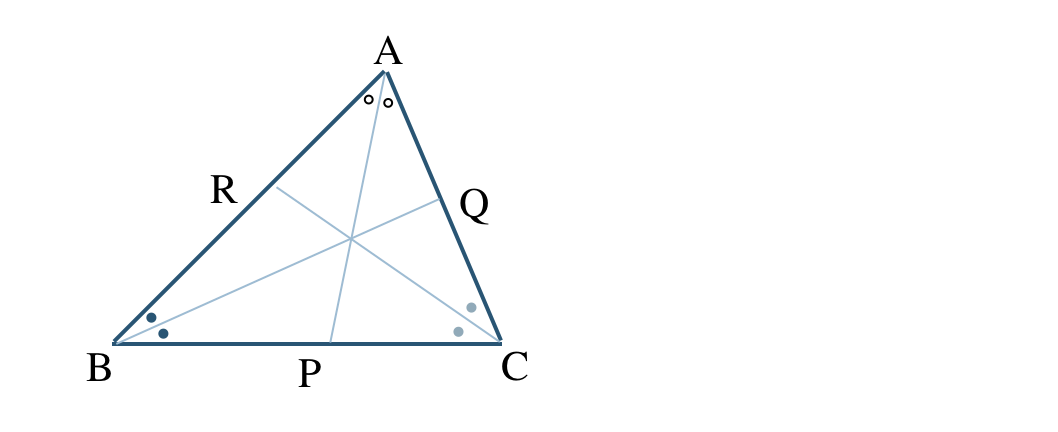
角の二等分線との交点を \({\rm P~,~Q~,~R}\) にすると、角の二等分線の比の関係より、$$\scriptsize~~~{\rm \frac{\,AR\,}{\,RB\,}=\frac{\,CA\,}{\,CB\,}~,~\frac{\,BP\,}{\,PC\,}=\frac{\,AB\,}{\,AC\,}~,~\frac{\,CQ\,}{\,QA\,}=\frac{\,BC\,}{\,BA\,}}$$これより、$$\scriptsize~~~{\rm \frac{\,AR\,}{\,RB\,}\cdot\frac{\,BP\,}{\,PC\,}\cdot\frac{\,CQ\,}{\,QA\,}=\frac{\,CA\,}{\,CB\,}\cdot\frac{\,AB\,}{\,AC\,}\cdot\frac{\,BC\,}{\,BA\,}=1}$$チェバの定理の逆が成り立つことより、3つの内角の二等分線は1点で交わる [終]
p.81 参考 問1[証明] \(\triangle {\rm ABC}\) において、3辺の条件は次のようになる
\({\rm AB+AC>BC}\) …①
\({\rm AC+BC>AB}\) …②
\({\rm AB+BC>AC}\) …③
②より、
\({\rm AB-AC<BC}\)
③より、
\({\rm AB-AC>-BC}\)
よって、
\({\rm -BC<AB-AC<BC}\)
\({\rm |AB-AC|<BC}\)
他の辺でも同様に成り立つので、
\({\rm |BA-BC|<AC}\)
\({\rm |CA-CB|<AB}\)
したがって、三角形の2辺の長さの差は、他の1辺の長さより小さい [終]
→ 三角形の辺と角の大小比較
\({\rm AB+AC>BC}\) …①
\({\rm AC+BC>AB}\) …②
\({\rm AB+BC>AC}\) …③
②より、
\({\rm AB-AC<BC}\)
③より、
\({\rm AB-AC>-BC}\)
よって、
\({\rm -BC<AB-AC<BC}\)
\({\rm |AB-AC|<BC}\)
他の辺でも同様に成り立つので、
\({\rm |BA-BC|<AC}\)
\({\rm |CA-CB|<AB}\)
したがって、三角形の2辺の長さの差は、他の1辺の長さより小さい [終]
→ 三角形の辺と角の大小比較
p.82 問題3[証明] \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) は高さの等しい三角形より、面積比=底辺の比であることより、
\(\triangle {\rm ABD}:\triangle {\rm ACD}={\rm BD:CD}\)
また、仮定より、
\(\triangle {\rm ABD}:\triangle {\rm ACD}={\rm AB:AC}\)
よって、
\({\rm BD:CD=AB:AC}\)
角の二等分線と比の関係が成り立つので、\({\rm AD}\) は \(\angle{\rm A}\) を二等分する [終]
\(\triangle {\rm ABD}:\triangle {\rm ACD}={\rm BD:CD}\)
また、仮定より、
\(\triangle {\rm ABD}:\triangle {\rm ACD}={\rm AB:AC}\)
よって、
\({\rm BD:CD=AB:AC}\)
角の二等分線と比の関係が成り立つので、\({\rm AD}\) は \(\angle{\rm A}\) を二等分する [終]
p.82 問題5[証明] 対角線 \({\rm BD}\) と \({\rm AC}\) の交点を \({\rm O}\) とすると、

\(\triangle {\rm ABD}\) において、チェバの定理より、$$~~~{\rm { \frac{AK}{KB}}\cdot{ \frac{BO}{OD}}\cdot{ \frac{DN}{NA}}}=1$$\(\triangle {\rm CBC}\) において、チェバの定理より、$$~~~{\rm { \frac{CM}{MD}}\cdot{ \frac{DO}{OB}}\cdot{ \frac{BL}{LC}}}=1$$これらの両辺をかけ合わせると、$$~~~{\rm { \frac{AK}{KB}}\cdot{ \frac{BL}{LC}}\cdot{ \frac{CM}{MD}}\cdot{ \frac{DN}{NA}}}=1$$[終]
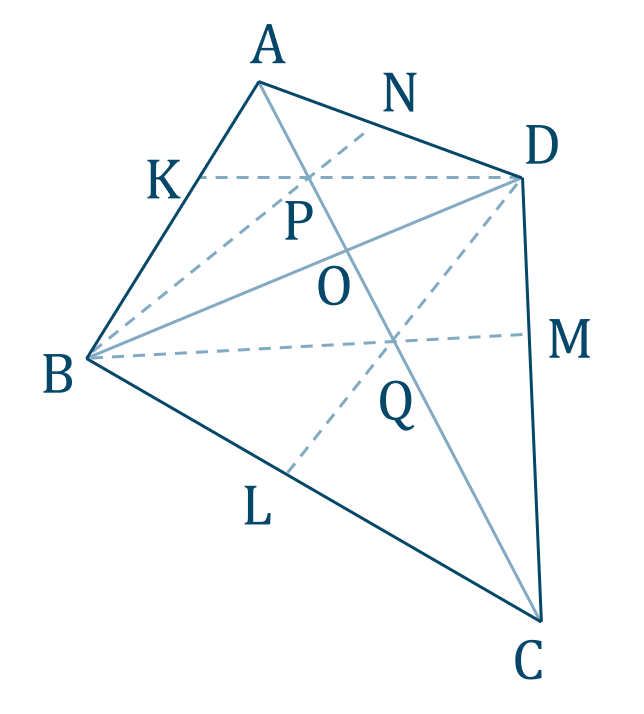
\(\triangle {\rm ABD}\) において、チェバの定理より、$$~~~{\rm { \frac{AK}{KB}}\cdot{ \frac{BO}{OD}}\cdot{ \frac{DN}{NA}}}=1$$\(\triangle {\rm CBC}\) において、チェバの定理より、$$~~~{\rm { \frac{CM}{MD}}\cdot{ \frac{DO}{OB}}\cdot{ \frac{BL}{LC}}}=1$$これらの両辺をかけ合わせると、$$~~~{\rm { \frac{AK}{KB}}\cdot{ \frac{BL}{LC}}\cdot{ \frac{CM}{MD}}\cdot{ \frac{DN}{NA}}}=1$$[終]
2節 円の性質
p.84 問1$${\small (1)}~40^\circ$$$${\small (2)}~20^\circ$$$${\small (3)}~140^\circ$$
p.85 問3$${\small (1)}~106^\circ$$$${\small (2)}~100^\circ$$$${\small (3)}~75^\circ$$
p.87 問5\({\small (1)}~\)[証明]
\(\angle{\rm AQP}=90^\circ~,~ \angle{\rm ARP}=90^\circ\)
よって、四角形 \({\rm ARPQ}\) の対角の和が \(180^\circ\) となるので、四角形 \({\rm ARPQ}\) は円に内接する
したがって、4点 \({\rm A~,~R~,~P~,~Q}\) は同一円周上にある [終]
\({\small (2)}~\)[証明]
\(\triangle {\rm ABP}\) と \(\triangle {\rm APR}\) について、
\(\angle{\rm APB}=\angle{\rm ARP}=90^\circ\)
\(\angle{\rm BAP}=\angle{\rm PAR}\) (共通角)
よって、2組の角がそれぞれ等しいので
\(\triangle {\rm ABP}\sim\triangle {\rm ARP}\)
これより、
\(\angle{\rm ABP}=\angle{\rm APR}\)
また、(1)より四角形 \({\rm ARPQ}\) は円に内接するので円周角の定理より、
\(\angle{\rm APR}=\angle{\rm AQR}\)
以上より、
\(\angle{\rm ABP}=\angle{\rm AQR}\)
よって、四角形 \({\rm BCQR}\) の1つの外角がその隣り合う内角の対角と等しいので四角形 \({\rm BCQR}\) は円に内接する
したがって、4点 \({\rm B~,~C~,~Q~,~R}\) は同一円周上にある [終]
\(\angle{\rm AQP}=90^\circ~,~ \angle{\rm ARP}=90^\circ\)
よって、四角形 \({\rm ARPQ}\) の対角の和が \(180^\circ\) となるので、四角形 \({\rm ARPQ}\) は円に内接する
したがって、4点 \({\rm A~,~R~,~P~,~Q}\) は同一円周上にある [終]
\({\small (2)}~\)[証明]
\(\triangle {\rm ABP}\) と \(\triangle {\rm APR}\) について、
\(\angle{\rm APB}=\angle{\rm ARP}=90^\circ\)
\(\angle{\rm BAP}=\angle{\rm PAR}\) (共通角)
よって、2組の角がそれぞれ等しいので
\(\triangle {\rm ABP}\sim\triangle {\rm ARP}\)
これより、
\(\angle{\rm ABP}=\angle{\rm APR}\)
また、(1)より四角形 \({\rm ARPQ}\) は円に内接するので円周角の定理より、
\(\angle{\rm APR}=\angle{\rm AQR}\)
以上より、
\(\angle{\rm ABP}=\angle{\rm AQR}\)
よって、四角形 \({\rm BCQR}\) の1つの外角がその隣り合う内角の対角と等しいので四角形 \({\rm BCQR}\) は円に内接する
したがって、4点 \({\rm B~,~C~,~Q~,~R}\) は同一円周上にある [終]
p.88 問6・直角の場合
[証明]

\(\angle{\rm BAT}=90^\circ\) で、\({\rm AB}\) ら直径となるので、$$~~~\angle{\rm ACB}=90^\circ$$したがって、$$~~~\angle{\rm BAT}=\angle{\rm ACB}$$[終]
・鈍角の場合
[証明]

直径 \({\rm AD}\) を引くと、円に内接する四角形より、$$~~~\angle{\rm ACB}=180^\circ-\angle{\rm BPA}~~~\cdots{\large ①}$$\(\triangle {\rm ABP}\) は直角三角形より、$$~~~\angle{\rm BAP}=90^\circ-\angle{\rm BPA}~~~\cdots{\large ②}$$また、\(\angle{\rm PAT}=90^\circ\) より、$$~~~\angle{\rm BAT}=\angle{\rm BAP}+90^\circ~~~\cdots{\large ③}$$②を代入すると、$$\begin{eqnarray}~~~\angle{\rm BAT}&=&(90^\circ-\angle{\rm BPA})+90^\circ\\[2pt]~~~&=&180^\circ-\angle{\rm BPA}\end{eqnarray}$$①より、$$~~~\angle{\rm BAT}=\angle{\rm ACB}$$[終]
→ 内接円と接線の条件
[証明]

\(\angle{\rm BAT}=90^\circ\) で、\({\rm AB}\) ら直径となるので、$$~~~\angle{\rm ACB}=90^\circ$$したがって、$$~~~\angle{\rm BAT}=\angle{\rm ACB}$$[終]
・鈍角の場合
[証明]

直径 \({\rm AD}\) を引くと、円に内接する四角形より、$$~~~\angle{\rm ACB}=180^\circ-\angle{\rm BPA}~~~\cdots{\large ①}$$\(\triangle {\rm ABP}\) は直角三角形より、$$~~~\angle{\rm BAP}=90^\circ-\angle{\rm BPA}~~~\cdots{\large ②}$$また、\(\angle{\rm PAT}=90^\circ\) より、$$~~~\angle{\rm BAT}=\angle{\rm BAP}+90^\circ~~~\cdots{\large ③}$$②を代入すると、$$\begin{eqnarray}~~~\angle{\rm BAT}&=&(90^\circ-\angle{\rm BPA})+90^\circ\\[2pt]~~~&=&180^\circ-\angle{\rm BPA}\end{eqnarray}$$①より、$$~~~\angle{\rm BAT}=\angle{\rm ACB}$$[終]
→ 内接円と接線の条件
p.89 問7$${\small (1)}~104^\circ$$$${\small (2)}~146^\circ$$$${\small (3)}~46^\circ$$→ 接弦定理
p.89 問8\({\small (1)}~\)等しい、円に内接する四角形の定理
\({\small (2)}~\)等しい、接線と弦のつくる角の定理
\({\small (3)}~\)等しい、円周角の定理
\({\small (2)}~\)等しい、接線と弦のつくる角の定理
\({\small (3)}~\)等しい、円周角の定理
p.90 問9$$~~~6$$
p.91 問10[証明] \(\triangle {\rm PAC}\) と \(\triangle {\rm PDB}\) において、
円周角の定理より、$$~~~\angle{\rm CAP}=\angle{\rm BDP}$$対頂角より、$$~~~\angle{\rm APC}=\angle{\rm DPB}$$よって、$$~~~\triangle {\rm PAC}∽\triangle {\rm PDB}$$これより、$$~~~{\rm PA:PD=PC:PB}$$したがって、$$~~~{\rm PA\cdot PB=PC\cdot PD}$$[終]
円周角の定理より、$$~~~\angle{\rm CAP}=\angle{\rm BDP}$$対頂角より、$$~~~\angle{\rm APC}=\angle{\rm DPB}$$よって、$$~~~\triangle {\rm PAC}∽\triangle {\rm PDB}$$これより、$$~~~{\rm PA:PD=PC:PB}$$したがって、$$~~~{\rm PA\cdot PB=PC\cdot PD}$$[終]
p.91 問11$${\small (1)}~8$$$${\small (2)}~3$$
p.92 問12$${\small (1)}~x=2\sqrt{7}$$$${\small (2)}~x=3~,~y=2\sqrt{6}$$→ 方べきの定理
p.93 問13\({\small (1)}~\)円に内接する四角形の定理
\({\small (2)}~\)円周角の定理
\({\small (2)}~\)円周角の定理
p.93 問14[証明] 方べきの定理より、$$~~~{\rm PA\cdot PB=PT^2}$$$$~~~{\rm PC\cdot PD=PT^2}$$よって、$$~~~{\rm PA\cdot PB=PC\cdot PD}$$したがって、方べきの定理の逆より、4点 \({\rm A~,~B~,~C~,~D}\) は同一円周上にある [終]
p.94 問15\({\small [1]}~4\)本
\({\small [2]}~3\)本
\({\small [3]}~2\)本
\({\small [4]}~1\)本
\({\small [5]}~0\)本
→ 2つの円の位置関係と共通接線
\({\small [2]}~3\)本
\({\small [3]}~2\)本
\({\small [4]}~1\)本
\({\small [5]}~0\)本
→ 2つの円の位置関係と共通接線
p.95 問16$${\small (1)}~4\sqrt{10}$$$${\small (2)}~2\sqrt{22}$$→ 共通接線の長さ
p.95 問17[証明] 点 \({\rm P}\) における接線 \({\rm PT}\) を引くと、

接弦定理より、
\(\angle{\rm ACP}=\angle{\rm APT}\)
\(\angle{\rm BDC}=\angle{\rm BPT}\)
よって、
\(\angle{\rm ACD}=\angle{\rm BDP}\)
同位角が等しいので、\({\rm AC}\,//\,{\rm BD}\) [終]
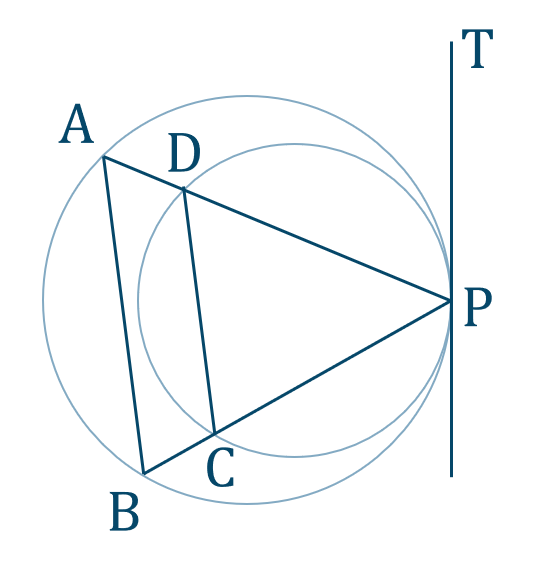
接弦定理より、
\(\angle{\rm ACP}=\angle{\rm APT}\)
\(\angle{\rm BDC}=\angle{\rm BPT}\)
よって、
\(\angle{\rm ACD}=\angle{\rm BDP}\)
同位角が等しいので、\({\rm AC}\,//\,{\rm BD}\) [終]
p.98 問題 7[証明]

円に内接する四角形 \({\rm BDPF}\) において、
\(\angle{\rm AFP}=\angle{\rm BDP}\)
また、円に内接する四角形 \({\rm DCEP}\) において、
\(\angle{\rm BDP}=\angle{\rm PEC}\)
よって、四角形 \({\rm AEPF}\) の1つの外角が隣り合う内角の対角と等しいので四角形 \({\rm AEPF}\) は円に内接する
したがって、4点 \({\rm A~,~E~,~P~,~F}\) は同一円周上にある [終]
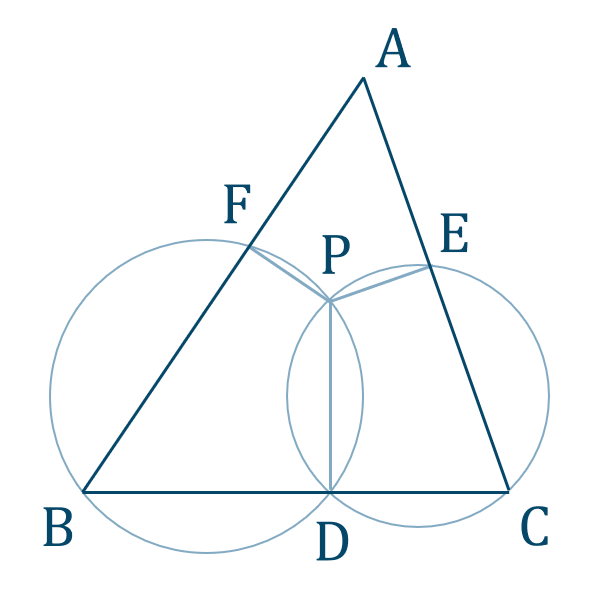
円に内接する四角形 \({\rm BDPF}\) において、
\(\angle{\rm AFP}=\angle{\rm BDP}\)
また、円に内接する四角形 \({\rm DCEP}\) において、
\(\angle{\rm BDP}=\angle{\rm PEC}\)
よって、四角形 \({\rm AEPF}\) の1つの外角が隣り合う内角の対角と等しいので四角形 \({\rm AEPF}\) は円に内接する
したがって、4点 \({\rm A~,~E~,~P~,~F}\) は同一円周上にある [終]
p.98 問題 9[証明] 点 \({\rm P}\) から円に2点で交わる直線を引き、交点を \({\rm A~,~B}\) とする

方べきの定理より、$$~~~{\rm PA\cdot PB=PS^2}$$$$~~~{\rm PA\cdot PB=PT^2}$$よって、$$~~~{\rm PS^2=PT^2}$$したがって、$$~~~{\rm PS=PT}$$[終]

方べきの定理より、$$~~~{\rm PA\cdot PB=PS^2}$$$$~~~{\rm PA\cdot PB=PT^2}$$よって、$$~~~{\rm PS^2=PT^2}$$したがって、$$~~~{\rm PS=PT}$$[終]
3節 空間図形
p.100 問1\({\small (1)}~\) 辺 \({\rm DC~,~HG~,~EF}\)
\({\small (2)}~\) 辺 \({\rm EH~,~FG~,~DH~,~CG}\)
→ 空間図形の位置関係
\({\small (2)}~\) 辺 \({\rm EH~,~FG~,~DH~,~CG}\)
→ 空間図形の位置関係
p.101 問2$${\small (1)}~90^\circ$$$${\small (2)}~45^\circ$$$${\small (3)}~60^\circ$$
p.103 問3$${\small (1)}~45^\circ$$$${\small (2)}~30^\circ$$$${\small (3)}~60^\circ$$
p.104 問4[証明] 四角形 \({\rm BCDE}\) は正方形で、対角線 \({\rm BD}\) と \({\rm CE}\) の交点 \({\rm O}\) はそれぞれの中点で交わる
また、\(\triangle {\rm ABD}\) において、
\({\rm AB=AD~,~BO=DO}\) より、
\({\rm AO\perp BD}\)
同様に、\(\triangle {\rm AEC}\) において、
\({\rm AO\perp EC}\)
直線 \({\rm AO}\) が平面 \({\rm BCDE}\) 上の2直線 \({\rm BD~,~CE}\) に垂直であるので
\({\rm AO}\perp\) 平面 \({\rm BCDE}\)
[終]
また、\(\triangle {\rm ABD}\) において、
\({\rm AB=AD~,~BO=DO}\) より、
\({\rm AO\perp BD}\)
同様に、\(\triangle {\rm AEC}\) において、
\({\rm AO\perp EC}\)
直線 \({\rm AO}\) が平面 \({\rm BCDE}\) 上の2直線 \({\rm BD~,~CE}\) に垂直であるので
\({\rm AO}\perp\) 平面 \({\rm BCDE}\)
[終]
p.104 問5[証明] \({\rm AH}\perp\triangle {\rm BCD}\)
また、仮定より \({\rm AP}\perp{\rm BC}\)
したがって、定理より、
\({\rm HP}\perp{\rm BC}\) [終]
また、仮定より \({\rm AP}\perp{\rm BC}\)
したがって、定理より、
\({\rm HP}\perp{\rm BC}\) [終]
p.105 問6[証明] \({\rm PO}\perp \alpha\) より、
\({\rm PO}\perp l\)
ゆえに \(l\) は平面 \({\rm AOP}\) 上の交わる2直線 \({\rm PO~,~PA}\) に垂直であるから
\(l\perp \) 平面 \({\rm AOP}\)
\({\rm OA}\) は平面 \({\rm AOP}\) 上にあるから
\({\rm OA}\perp l\)
[終]
\({\rm PO}\perp l\)
ゆえに \(l\) は平面 \({\rm AOP}\) 上の交わる2直線 \({\rm PO~,~PA}\) に垂直であるから
\(l\perp \) 平面 \({\rm AOP}\)
\({\rm OA}\) は平面 \({\rm AOP}\) 上にあるから
\({\rm OA}\perp l\)
[終]
p.106 問7[証明] \({\rm AH\perp\triangle {\rm BCD}}\) より、
\({\rm AH\perp CD}\)
また、\({\rm {\rm AB\perp CD}}\) であるので、
面 \({\rm ABH \perp CD}\)
これより、
\({\rm BH\perp CD}~~~\cdots{\large ①}\)
また、同様に考えて、
\({\rm CH\perp BD}~~~\cdots{\large ②}\)
①、②より頂点から対辺に引いた垂線の交点となるので、
点 \({\rm H}\) は \(\triangle {\rm BCD}\) の垂心となる
[終]
\({\rm AH\perp CD}\)
また、\({\rm {\rm AB\perp CD}}\) であるので、
面 \({\rm ABH \perp CD}\)
これより、
\({\rm BH\perp CD}~~~\cdots{\large ①}\)
また、同様に考えて、
\({\rm CH\perp BD}~~~\cdots{\large ②}\)
①、②より頂点から対辺に引いた垂線の交点となるので、
点 \({\rm H}\) は \(\triangle {\rm BCD}\) の垂心となる
[終]
p.107 問8[証明]応用例題3より、
\({\rm CE}\) は \(\triangle {\rm AFH}\) の重心を通る
また、\(\triangle {\rm AFH}\) は正三角形であり、垂心と重心は一致する
よって、\({\rm CE}\) は \(\triangle {\rm AFH}\) の垂心を通るので、
\({\rm CE}\perp\) 平面 \({\rm AFH}\)
[終]
\({\rm CE}\) は \(\triangle {\rm AFH}\) の重心を通る
また、\(\triangle {\rm AFH}\) は正三角形であり、垂心と重心は一致する
よって、\({\rm CE}\) は \(\triangle {\rm AFH}\) の垂心を通るので、
\({\rm CE}\perp\) 平面 \({\rm AFH}\)
[終]
練習問題 図形の性質
p.110 練習問題A 1[証明]

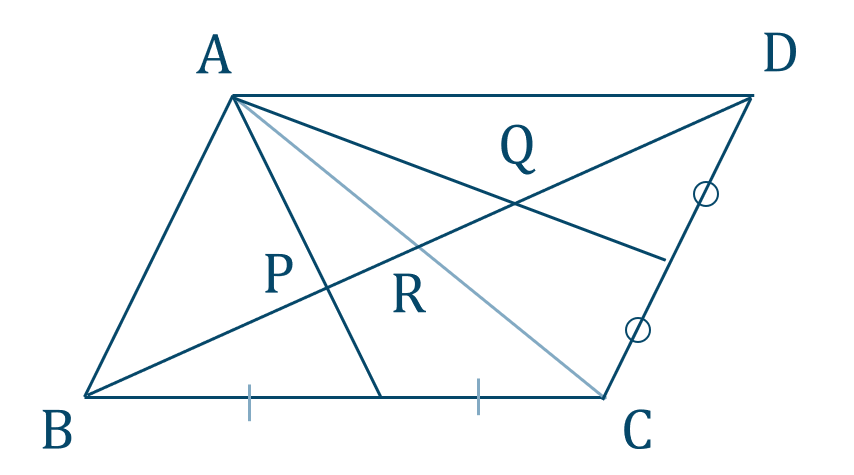
対角線 \({\rm AC}\) を引き、対角線の交点を \({\rm R}\) とすると、
この交点は対角線の中点で交わるので、
\({\rm AR=CR}\)
\({\rm BR=DR}\)
次に、仮定より \({\rm BM:MC}\)
よって、点 \({\rm P}\) は \(\triangle {\rm ABC}\) の重心となり
\({\rm BP:PR}=2:1\)
同様に、仮定より \({\rm CN:ND}\)
よって、点 \({\rm Q}\) は \(\triangle {\rm ACD}\) の重心となり
\({\rm DQ:QR}=2:1\)
以上より、
\({\rm BP:PR+QR:DQ}=2:1+1:2\)
したがって、
\({\rm BP=PQ=QD}\) [終]
対角線 \({\rm AC}\) を引き、対角線の交点を \({\rm R}\) とすると、
この交点は対角線の中点で交わるので、
\({\rm AR=CR}\)
\({\rm BR=DR}\)
次に、仮定より \({\rm BM:MC}\)
よって、点 \({\rm P}\) は \(\triangle {\rm ABC}\) の重心となり
\({\rm BP:PR}=2:1\)
同様に、仮定より \({\rm CN:ND}\)
よって、点 \({\rm Q}\) は \(\triangle {\rm ACD}\) の重心となり
\({\rm DQ:QR}=2:1\)
以上より、
\({\rm BP:PR+QR:DQ}=2:1+1:2\)
したがって、
\({\rm BP=PQ=QD}\) [終]
p.110 練習問題A 2[証明]

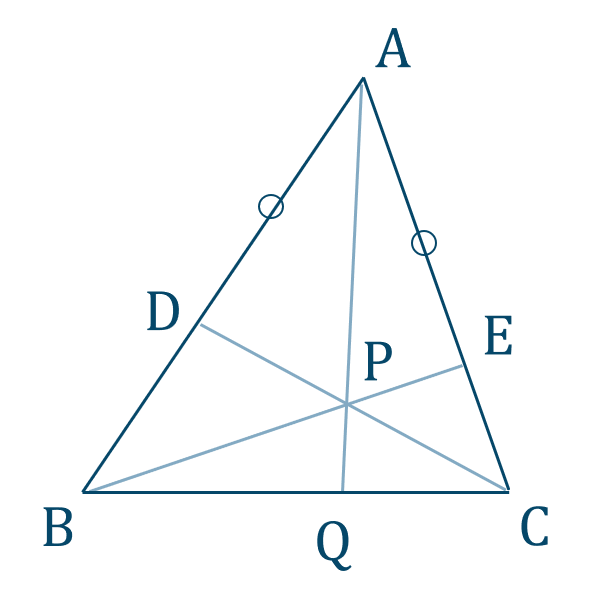
\(\triangle {\rm ABC}\) について、チェバの定理より、
\({\rm {\large \frac{AD}{DB}}\cdot{\large \frac{BQ}{QC}}\cdot{\large \frac{CE}{EA}}=1}\)
ここで、\({\rm AD=AE}\) より、
\({\rm {\large \frac{1}{DB}}\cdot{\large \frac{BQ}{QC}}\cdot{\large \frac{CE}{1}}=1}\)
よって、
\({\rm BQ:QC=BD:CE}\)
したがって、点 \({\rm Q}\) は \({\rm BC}\) を \({\rm BD:CE}\) に内分する [終]
\(\triangle {\rm ABC}\) について、チェバの定理より、
\({\rm {\large \frac{AD}{DB}}\cdot{\large \frac{BQ}{QC}}\cdot{\large \frac{CE}{EA}}=1}\)
ここで、\({\rm AD=AE}\) より、
\({\rm {\large \frac{1}{DB}}\cdot{\large \frac{BQ}{QC}}\cdot{\large \frac{CE}{1}}=1}\)
よって、
\({\rm BQ:QC=BD:CE}\)
したがって、点 \({\rm Q}\) は \({\rm BC}\) を \({\rm BD:CE}\) に内分する [終]
p.110 練習問題A 4[証明]

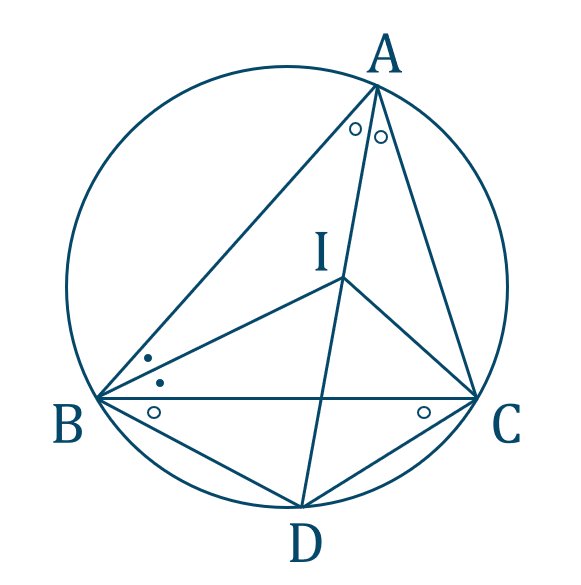
点 \({\rm I}\) は \(\triangle {\rm ABC}\) の内心より、
\(\angle{\rm BAD}=\angle{\rm DAC}=x\)
また、円周角の定理より、
\(\angle{\rm CBD}=\angle{\rm BCD}=x\)
\(\triangle {\rm DBC}\) は底角が等しい二等辺三角形より、
\({\rm DB=DC}\)
次に、\({\rm BI}\) が \(\angle{\rm B}\) の二等分線より、
\(\angle{\rm ABI}=\angle{\rm IBC}=y\)
ここで、\(\triangle {\rm AIB}\) の外角より、
\(\angle{\rm BID}=x+y\)
また、\(\angle{\rm IBD}=x+y\)
よって、\(\triangle {\rm DBI}\) は底角が等しい二等辺三角形より、
\({\rm DB=DI}\)
したがって、\({\rm DI=DB=DC}\) [終]
点 \({\rm I}\) は \(\triangle {\rm ABC}\) の内心より、
\(\angle{\rm BAD}=\angle{\rm DAC}=x\)
また、円周角の定理より、
\(\angle{\rm CBD}=\angle{\rm BCD}=x\)
\(\triangle {\rm DBC}\) は底角が等しい二等辺三角形より、
\({\rm DB=DC}\)
次に、\({\rm BI}\) が \(\angle{\rm B}\) の二等分線より、
\(\angle{\rm ABI}=\angle{\rm IBC}=y\)
ここで、\(\triangle {\rm AIB}\) の外角より、
\(\angle{\rm BID}=x+y\)
また、\(\angle{\rm IBD}=x+y\)
よって、\(\triangle {\rm DBI}\) は底角が等しい二等辺三角形より、
\({\rm DB=DI}\)
したがって、\({\rm DI=DB=DC}\) [終]
p.111 練習問題B 6[証明]

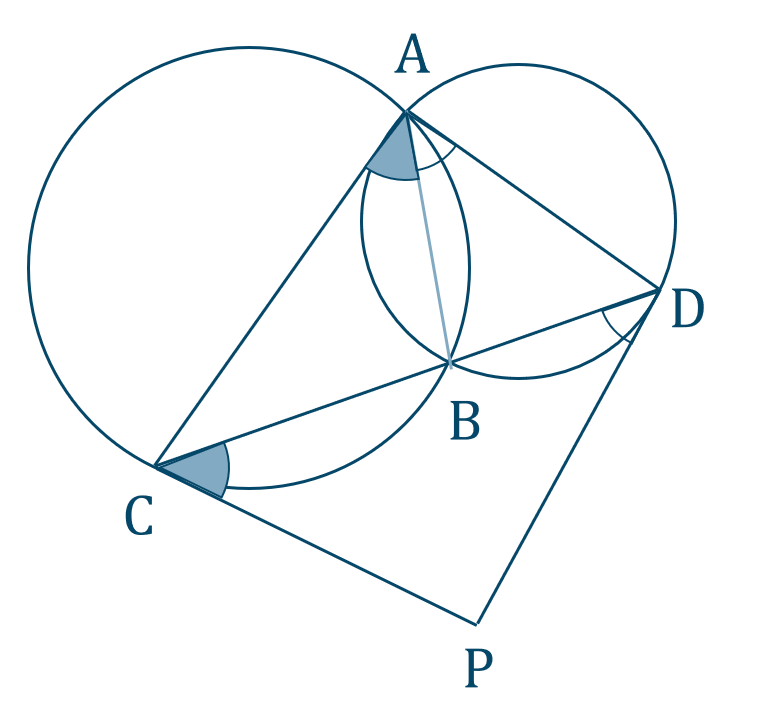
弦 \({\rm AB}\) を引くと、接弦定理より、
\(\angle{\rm PCD}=\angle{\rm CAB}=x\)
\(\angle{\rm PDC}=\angle{\rm DAB}=y\)
よって、\(\angle{\rm CAD}=x+y\)
次に、\(\triangle {\rm CPD}\) の内角の和について、
\(\angle{\rm CPD}=180^\circ-(x+y)\)
よって、
\(\angle{\rm CAD}=\angle{\rm CPD}=180^\circ\)
対角の和が \(180^\circ\) となるので、
四角形 \({\rm ACPD}\) は円に内接する [終]
弦 \({\rm AB}\) を引くと、接弦定理より、
\(\angle{\rm PCD}=\angle{\rm CAB}=x\)
\(\angle{\rm PDC}=\angle{\rm DAB}=y\)
よって、\(\angle{\rm CAD}=x+y\)
次に、\(\triangle {\rm CPD}\) の内角の和について、
\(\angle{\rm CPD}=180^\circ-(x+y)\)
よって、
\(\angle{\rm CAD}=\angle{\rm CPD}=180^\circ\)
対角の和が \(180^\circ\) となるので、
四角形 \({\rm ACPD}\) は円に内接する [終]
p.111 練習問題B 8\({\small (1)}~\)[証明]
\(\triangle {\rm DBC}\) と \(\triangle {\rm DAE}\) について、
\(\angle{\rm CDE}=\angle{\rm BDA}\) (仮定)
\(\angle{\rm BDE}\) (共通角)
これらより、
\(\angle{\rm BDC}=\angle{\rm ADE}\)
また、円周角の定理より、
\(\angle{\rm DBC}=\angle{\rm DAE}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm DBC}\sim\triangle {\rm DAE}\) [終]
\({\small (2)}~\)[証明]
\(\triangle {\rm DAB}\) と \(\triangle {\rm DEC}\) について、
円周角の定理より、
\(\angle{\rm ABD}=\angle{\rm DCE}\)
仮定より、
\(\angle{\rm ADB}=\angle{\rm CDE}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm DAB}\sim\triangle {\rm DEC}\)
よって、対応する辺の比が等しいので、
\({\rm AB:EC=BD:CD}\)
これより、
\({\rm AB\cdot CD=EC\cdot BD}\) …①
また、(1)の結果の \(\triangle {\rm DBC}\sim\triangle {\rm DAE}\) より、対応する辺の比が等しいので、
\({\rm BC:AE=BD:AD}\)
これより、
\({\rm AD\cdot BC=AE\cdot BD}\) …②
①と②の両辺を加えると、
\({\rm AB\cdot CD+BD\cdot BC}\)
\(={\rm EC\cdot BD+AE\cdot BD}\)
\(={\rm (EC+AE)\cdot BD}\)
\(={\rm AC\cdot BD}\)
したがって、
\({\rm AB\cdot CD+BD\cdot BC=AC\cdot BD}\) [終]
\(\triangle {\rm DBC}\) と \(\triangle {\rm DAE}\) について、
\(\angle{\rm CDE}=\angle{\rm BDA}\) (仮定)
\(\angle{\rm BDE}\) (共通角)
これらより、
\(\angle{\rm BDC}=\angle{\rm ADE}\)
また、円周角の定理より、
\(\angle{\rm DBC}=\angle{\rm DAE}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm DBC}\sim\triangle {\rm DAE}\) [終]
\({\small (2)}~\)[証明]
\(\triangle {\rm DAB}\) と \(\triangle {\rm DEC}\) について、
円周角の定理より、
\(\angle{\rm ABD}=\angle{\rm DCE}\)
仮定より、
\(\angle{\rm ADB}=\angle{\rm CDE}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm DAB}\sim\triangle {\rm DEC}\)
よって、対応する辺の比が等しいので、
\({\rm AB:EC=BD:CD}\)
これより、
\({\rm AB\cdot CD=EC\cdot BD}\) …①
また、(1)の結果の \(\triangle {\rm DBC}\sim\triangle {\rm DAE}\) より、対応する辺の比が等しいので、
\({\rm BC:AE=BD:AD}\)
これより、
\({\rm AD\cdot BC=AE\cdot BD}\) …②
①と②の両辺を加えると、
\({\rm AB\cdot CD+BD\cdot BC}\)
\(={\rm EC\cdot BD+AE\cdot BD}\)
\(={\rm (EC+AE)\cdot BD}\)
\(={\rm AC\cdot BD}\)
したがって、
\({\rm AB\cdot CD+BD\cdot BC=AC\cdot BD}\) [終]
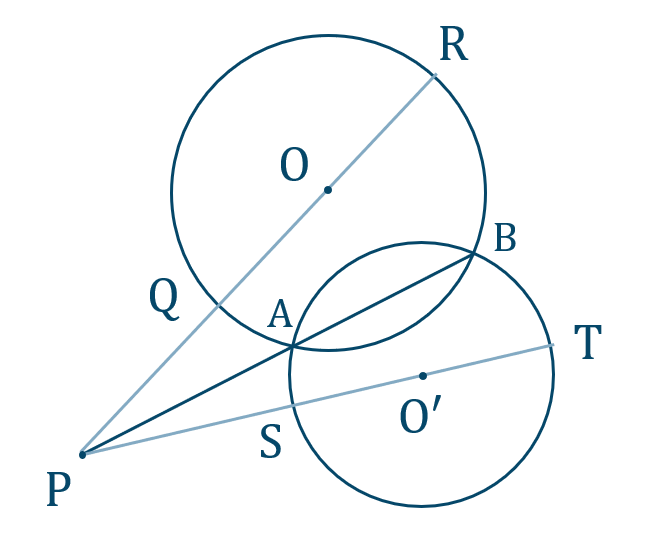
p.111 練習問題B 9[証明]

図のように \({\rm Q~,~R~,~S~,~T}\) をとると、
方べきの定理より、
\({\rm PA\cdot PB=PQ\cdot PR}\)
\({\rm PA\cdot PB=PS\cdot PT}\)
よって、
\({\rm PQ\cdot PR=PS\cdot PT}\) …①
また、
\({\rm PQ=PO}-r\)
\({\rm PR=PO}+r\)
\({\rm PS=PO’}-r’\)
\({\rm PT=PO’}+r’\)
①に代入すると、
\(({\rm PO}-r)({\rm PO}+r)\)
\(=({\rm PO’}-r’)({\rm PO’}+r’)\)
したがって、
\({\rm PO}^2-r^2={\rm PO’}^2-r’^2\) [終]
図のように \({\rm Q~,~R~,~S~,~T}\) をとると、
方べきの定理より、
\({\rm PA\cdot PB=PQ\cdot PR}\)
\({\rm PA\cdot PB=PS\cdot PT}\)
よって、
\({\rm PQ\cdot PR=PS\cdot PT}\) …①
また、
\({\rm PQ=PO}-r\)
\({\rm PR=PO}+r\)
\({\rm PS=PO’}-r’\)
\({\rm PT=PO’}+r’\)
①に代入すると、
\(({\rm PO}-r)({\rm PO}+r)\)
\(=({\rm PO’}-r’)({\rm PO’}+r’)\)
したがって、
\({\rm PO}^2-r^2={\rm PO’}^2-r’^2\) [終]
p.111 練習問題B 10[証明] 正三角形 \({\rm ABC}\) より、
\({\rm AM\perp BC}~~~\cdots{\large ①}\)
正三角形 \({\rm DBC}\) より、
\({\rm DM\perp BC}\)
これより、
\({\rm HM\perp BC}~~~\cdots{\large ②}\)
①、②より、
\(\triangle {\rm AMH\perp BC}\)
よって、
\({\rm AH\perp BC}\)
また、\({\rm AH\perp DM}\) であるので、
\({\rm AH}\perp\) 平面 \({\rm BCD}\)
[終]
\({\rm AM\perp BC}~~~\cdots{\large ①}\)
正三角形 \({\rm DBC}\) より、
\({\rm DM\perp BC}\)
これより、
\({\rm HM\perp BC}~~~\cdots{\large ②}\)
①、②より、
\(\triangle {\rm AMH\perp BC}\)
よって、
\({\rm AH\perp BC}\)
また、\({\rm AH\perp DM}\) であるので、
\({\rm AH}\perp\) 平面 \({\rm BCD}\)
[終]
次のページ「3章 数学の人間の活動」