このページは、数研出版:高等学校数学Ⅰ[713]
第4章 図形と計量
第4章 図形と計量

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
高等学校数学Ⅰ 第1章 数と式
高等学校数学Ⅰ 第2章 集合と命題
高等学校数学Ⅰ 第3章 2次関数
高等学校数学Ⅰ 第4章 図形と計量
高等学校数学Ⅰ 第5章 データの分析
第4章 図形と計量
第1節 三角比
p.130 練習1$${\small (1)}~\sin{\theta}={ \frac{\,2\,}{\,3\,}}~,~\cos{\theta}={ \frac{\,\sqrt{5}\,}{\,3\,}}$$$$~~~~~~\tan{\theta}={ \frac{\,2\,}{\,\sqrt{5}\,}}$$$${\small (2)}~\sin{\theta}={ \frac{\,5\,}{\,13\,}}~,~\cos{\theta}={ \frac{\,12\,}{\,13\,}}$$$$~~~~~~\tan{\theta}={ \frac{\,5\,}{\,12\,}}$$$${\small (3)}~\sin{\theta}={ \frac{\,\sqrt{7}\,}{\,4\,}}~,~\cos{\theta}={ \frac{\,3\,}{\,4\,}}$$$$~~~~~~\tan{\theta}={ \frac{\,\sqrt{7}\,}{\,3\,}}$$→ 直角三角形と三角比
p.130 練習2
| \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | |
| \(\sin{}\) | \({\large \frac{\,1\,}{\,2\,}}\) | \({\large \frac{\,1\,}{\,\sqrt{2}\,}}\) | \({\large \frac{\,\sqrt{3}\,}{\,2\,}}\) |
| \(\cos{}\) | \({\large \frac{\,\sqrt{3}\,}{\,2\,}}\) | \({\large \frac{\,1\,}{\,\sqrt{2}\,}}\) | \({\large \frac{\,1\,}{\,2\,}}\) |
| \(\tan{}\) | \({\large \frac{\,1\,}{\,\sqrt{3}\,}}\) | \(1\) | \(\sqrt{3}\) |
p.131 練習3$${\small (1)}~0.2079$$$${\small (2)}~0.6691$$$${\small (3)}~3.7321$$
p.131 練習4$${\small (1)}~24^\circ$$$${\small (2)}~27^\circ$$
p.132 練習5$$~~~95~{\rm m}$$
p.133 練習6$$~~~32~{\rm m}$$
p.135 練習7$$~~~\sin{\theta}={ \frac{\,2\sqrt{2}\,}{\,3\,}}~,~\tan{\theta}=2\sqrt{2}$$
p.135 練習8$$~~~\cos{\theta}={ \frac{\,\sqrt{3}\,}{\,3\,}}~,~\sin{\theta}={ \frac{\,\sqrt{6}\,}{\,3\,}}$$→ 三角比の相互関係の公式(鋭角)
p.136 練習9$${\small (1)}~28^\circ$$$${\small (2)}~12^\circ$$$${\small (3)}~67^\circ$$
p.136 練習10$${\small (1)}~\cos{26^\circ}$$$${\small (2)}~\sin{32^\circ}$$$${\small (3)}~{ \frac{\,1\,}{\,\tan{7^\circ}\,}}$$→ 余角の公式
p.136 深める\(\theta\) が \(0^\circ\) から \(90^\circ\) の \(\sin{\theta}\) と \(\cos{\theta}\) の値は、\(\theta=45^\circ\) の値を基準として対称的に並ぶ
p.138 練習11$${\small (1)}~r=\sqrt{2}~,~(-1,1)$$$$~~~\sin{135^\circ}={ \frac{\,1\,}{\,\sqrt{2}\,}}~,~\cos{135^\circ}=-{ \frac{\,1\,}{\,\sqrt{2}\,}}$$$$~~~\tan{135^\circ}=-1$$$${\small (2)}~r=2~,~(-\sqrt{3},1)$$$$~~~\sin{150^\circ}={ \frac{\,1\,}{\,2\,}}~,~\cos{150^\circ}=-{ \frac{\,\sqrt{3}\,}{\,2\,}}$$$$~~~\tan{150^\circ}=-{ \frac{\,1\,}{\,\sqrt{3}\,}}$$→ 三角比の拡張
p.140 練習12$${\small (1)}~0.6428$$$${\small (2)}~-0.9135$$$${\small (3)}~-5.6713$$→ 補角の公式
p.141 練習13$${\small (1)}~60^\circ~,~120^\circ$$$${\small (2)}~120^\circ$$$${\small (3)}~0^\circ~,~180^\circ$$
p.142 練習14$${\small (1)}~45^\circ$$$${\small (2)}~150^\circ$$→ 三角比と方程式
p.143 練習15\(0^\circ< \theta < 90^\circ\) のとき$$~~~\cos{\theta}={ \frac{\,3\,}{\,5\,}}~,~\tan{\theta}={ \frac{\,4\,}{\,3\,}}$$\(90^\circ< \theta < 180^\circ\) のとき$$~~~\cos{\theta}=-{ \frac{\,3\,}{\,5\,}}~,~\tan{\theta}=-{ \frac{\,4\,}{\,3\,}}$$
p.143 練習16$${\small (1)}~\sin{\theta}={ \frac{\,2\sqrt{2}\,}{\,3\,}}~,~\tan{\theta}=-2\sqrt{2}$$$${\small (2)}~\cos{\theta}=-{ \frac{\,1\,}{\,\sqrt{5}\,}}~,~\sin{\theta}={ \frac{\,2\,}{\,\sqrt{5}\,}}$$→ 三角比の相互関係の公式(鈍角)
p.144 練習17$${\small (1)}~45^\circ$$$${\small (2)}~120^\circ$$→ 直線の傾きと正接
p.145 問題 2\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
これより、$$~~~{ \frac{\,{\rm B+C}\,}{\,2\,}}=90^\circ-{ \frac{\,{\rm A}\,}{\,2\,}}$$ここで、\(\cos{(90^\circ-\theta)}=\sin{\theta}\) より、$$~~~\cos{\left(90^\circ-{ \frac{\,{\rm A}\,}{\,2\,}}\right)}=\sin{{ \frac{\,{\rm A}\,}{\,2\,}}}$$したがって、$$~~~\sin{{ \frac{\,{\rm A}\,}{\,2\,}}}=\cos{{ \frac{\,{\rm B+C}\,}{\,2\,}}}$$[終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\sin{(180^\circ-\theta)}=\sin{\theta}\) より、
\(\sin{(180^\circ-{\rm A})}=\sin{{\rm A}}\)
したがって、
\(\sin{{\rm A}}=\sin{({\rm B+C})}\)
[終]
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
これより、$$~~~{ \frac{\,{\rm B+C}\,}{\,2\,}}=90^\circ-{ \frac{\,{\rm A}\,}{\,2\,}}$$ここで、\(\cos{(90^\circ-\theta)}=\sin{\theta}\) より、$$~~~\cos{\left(90^\circ-{ \frac{\,{\rm A}\,}{\,2\,}}\right)}=\sin{{ \frac{\,{\rm A}\,}{\,2\,}}}$$したがって、$$~~~\sin{{ \frac{\,{\rm A}\,}{\,2\,}}}=\cos{{ \frac{\,{\rm B+C}\,}{\,2\,}}}$$[終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\sin{(180^\circ-\theta)}=\sin{\theta}\) より、
\(\sin{(180^\circ-{\rm A})}=\sin{{\rm A}}\)
したがって、
\(\sin{{\rm A}}=\sin{({\rm B+C})}\)
[終]
第2節 三角形への応用
p.148 練習18$${\small (1)}~{ \frac{\,5\sqrt{2}\,}{\,2\,}}$$$${\small (2)}~1$$
p.148 練習19$$~~~30^\circ~,~150^\circ$$
p.149 練習20$${\small (1)}~b=1$$$${\small (2)}~c=\sqrt{6}$$→ 正弦定理
p.149 練習21$$~~~200\sqrt{2}~{\rm m}$$
p.150 練習22[証明] \(\triangle {\rm CDB}\) において三平方の定理より、
\({\rm BC}^2={\rm CD}^2+{\rm BD}^2\)
次に、\(\triangle {\rm CAD}\) において
\(\sin{(180^\circ-{\rm A})}={\large \frac{{\rm CD}}{b}}\)
よって、
\(b\sin{{\rm A}}={\rm CD}\)
2乗すると、
\({\rm CD}^2=(b\sin{{\rm A}})^2\)
また、\(\triangle {\rm CAD}\) において、$$~~~\cos{(180^\circ-{\rm A})}={ \frac{\,{\rm AD}\,}{\,b\,}}$$よって、
\(-b\cos{{\rm A}}={\rm AD}\)
ここで、\({\rm BD=AB+AD}\) より、
\({\rm BD}=c-b\cos{{\rm A}}\)
2乗すると、
\({\rm BD}^2=(c-b\cos{{\rm A}})^2\) [終]
\({\rm BC}^2={\rm CD}^2+{\rm BD}^2\)
次に、\(\triangle {\rm CAD}\) において
\(\sin{(180^\circ-{\rm A})}={\large \frac{{\rm CD}}{b}}\)
よって、
\(b\sin{{\rm A}}={\rm CD}\)
2乗すると、
\({\rm CD}^2=(b\sin{{\rm A}})^2\)
また、\(\triangle {\rm CAD}\) において、$$~~~\cos{(180^\circ-{\rm A})}={ \frac{\,{\rm AD}\,}{\,b\,}}$$よって、
\(-b\cos{{\rm A}}={\rm AD}\)
ここで、\({\rm BD=AB+AD}\) より、
\({\rm BD}=c-b\cos{{\rm A}}\)
2乗すると、
\({\rm BD}^2=(c-b\cos{{\rm A}})^2\) [終]
p.151 練習23$${\small (1)}~b=\sqrt{5}$$$${\small (2)}~c=7$$→ 余弦定理
p.151 練習24$$~~~10\sqrt{21}~{\rm m}$$
p.152 練習25$${\small (1)}~{\rm A}=30^\circ$$$${\small (2)}~{\rm B}=135^\circ$$→ 余弦定理
p.154 練習27$$~~~b=2~,~{\rm A}=30^\circ~,~{\rm C}=105^\circ$$
p.154 深める\({\rm A}=60^\circ\) であり、\({\rm B}=135^\circ\) であると内角の和が \(180^\circ\) より大きくなり、三角形とならない
p.155 練習28$$~~~{\rm C}=120^\circ$$
p.157 練習29$${\small (1)}~20\sqrt{2}$$$${\small (2)}~{ \frac{\,15\,}{\,2\,}}$$$${\small (3)}~{ \frac{\,\sqrt{3}\,}{\,4\,}}a^2$$
p.157 練習30$${\small (1)}~10\sqrt{3}$$$${\small (2)}~84$$→ 三角形の面積(三角比)
p.158 練習31$$~~~6\sqrt{3}$$→ 円に内接する四角形
p.159 練習32$$~~~{ \frac{\,\sqrt{15}\,}{\,6\,}}$$→ 内接円の半径
p.160 発展 練習1$$~~~14\sqrt{3}$$
p.161 練習33$$~~~50\sqrt{2}~{\rm m}$$
p.162 練習34$$~~~3\sqrt{29}$$→ 直方体の計量
p.163 研究 練習1$$~~~{ \frac{\,4\sqrt{11}\,}{\,3\,}}$$
章末問題 図形と計量
p.165 章末問題A 3[証明]

\(\triangle {\rm AOD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(\triangle {\rm AOB}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(\triangle {\rm BOC}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(\triangle {\rm OCD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
これら4つの三角形の面積の和が、四角形の面積 \(S\) となるので、
\(S= {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(+ {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(~+{\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(~~+ {\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
因数分解すると、
\(S={\large \frac{1}{2}}({\rm OA+OC})({\rm OB+OD})\sin{\theta}\)
ここで、\({\rm OA+OC}=p~,~{\rm OB+OD}=q\) より、
\(S={\large \frac{1}{2}}pq\sin{\theta}\) [終]
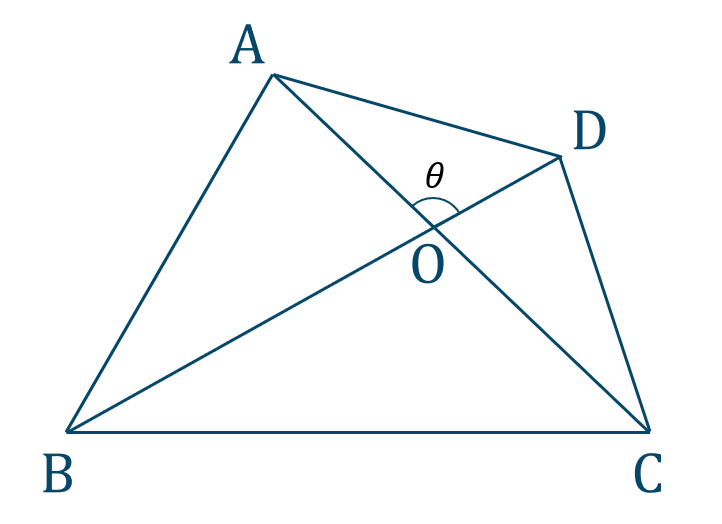
\(\triangle {\rm AOD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(\triangle {\rm AOB}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(\triangle {\rm BOC}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(\triangle {\rm OCD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
これら4つの三角形の面積の和が、四角形の面積 \(S\) となるので、
\(S= {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(+ {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(~+{\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(~~+ {\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
因数分解すると、
\(S={\large \frac{1}{2}}({\rm OA+OC})({\rm OB+OD})\sin{\theta}\)
ここで、\({\rm OA+OC}=p~,~{\rm OB+OD}=q\) より、
\(S={\large \frac{1}{2}}pq\sin{\theta}\) [終]
次のページ「第5章 データの分析」


