このページは、数研出版:高等学校数学Ⅰ[713]
第3章 2次関数
第3章 2次関数

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介 高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
高等学校数学Ⅰ 第1章 数と式
高等学校数学Ⅰ 第2章 集合と命題
高等学校数学Ⅰ 第3章 2次関数
高等学校数学Ⅰ 第4章 図形と計量
高等学校数学Ⅰ 第5章 データの分析
第3章 2次関数
第1節 2次関数とグラフ
p.75 練習1$${\small (1)}~4$$$${\small (2)}~4$$$${\small (3)}~a^2+2a+1$$$${\small (4)}~a^2$$
p.75 練習2$$~~~y=2x~(x≧4)$$
p.76 練習3\({\small (1)}~\)第1象限
\({\small (2)}~\)第4象限
\({\small (3)}~\)第2象限
\({\small (4)}~\)第3象限
→ 関数の値と象限
\({\small (2)}~\)第4象限
\({\small (3)}~\)第2象限
\({\small (4)}~\)第3象限
→ 関数の値と象限
p.76 深める$$~~~y=x+3$$点 \((-1~,~-1)\) は通らない
p.77 練習4\({\small (1)}~-2≦y≦7\)

\({\small (2)}~0≦y≦8\)

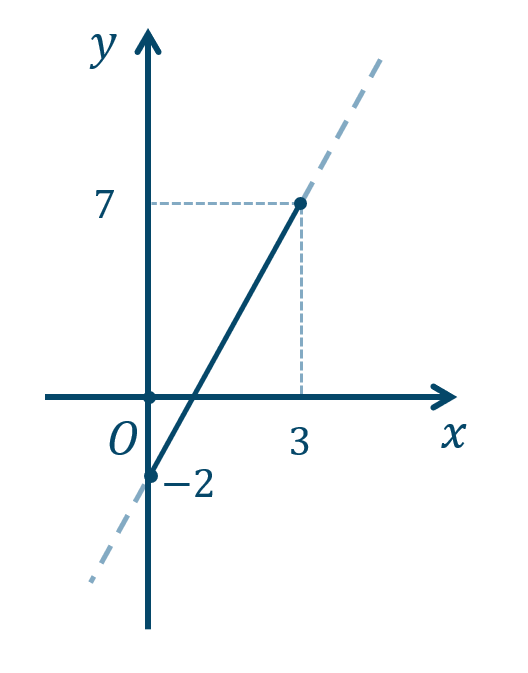
\({\small (2)}~0≦y≦8\)
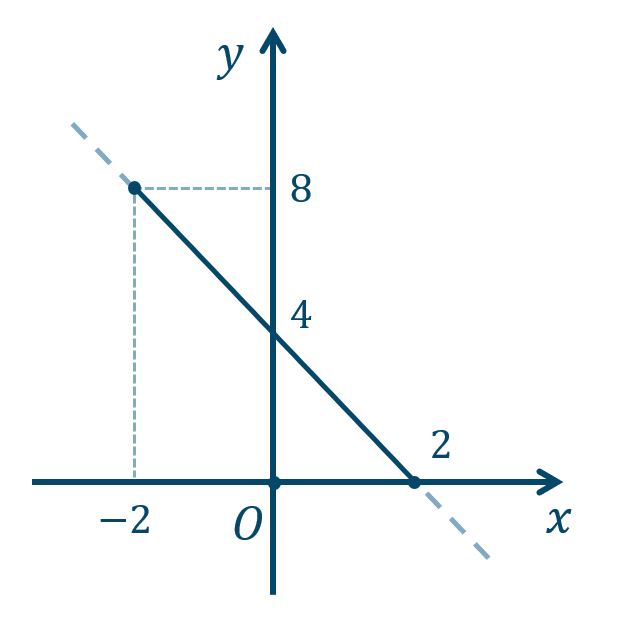
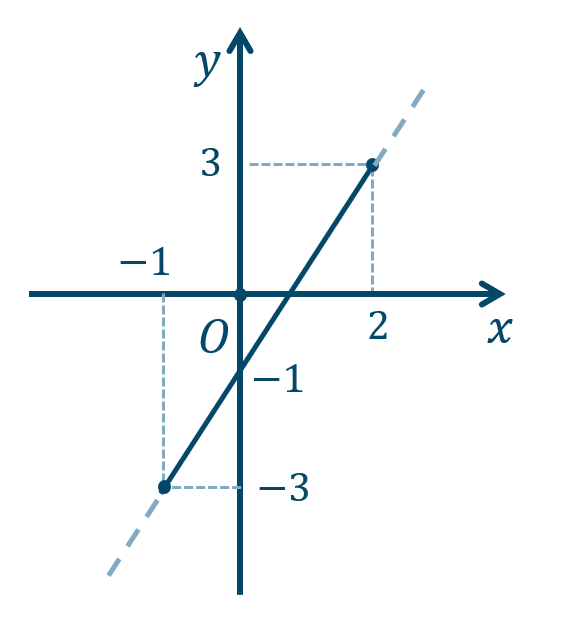
p.77 練習5\({\small (1)}~-3≦y≦3\)
\(x=2\) で、最大値 \(3\)
\(x=-1\) で、最大値 \(-3\)

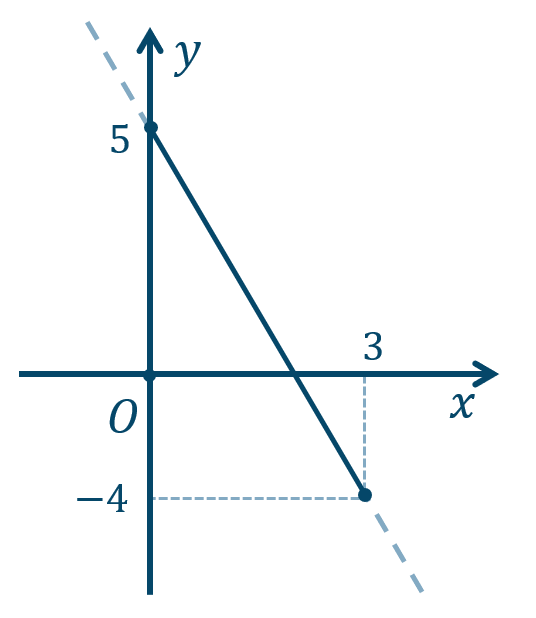
\({\small (2)}~-4≦y≦5\)
\(x=0\) で、最大値 \(5\)
\(x=3\) で、最大値 \(-4\)

→ 関数の値域と最大値・最小値
\(x=2\) で、最大値 \(3\)
\(x=-1\) で、最大値 \(-3\)
\({\small (2)}~-4≦y≦5\)
\(x=0\) で、最大値 \(5\)
\(x=3\) で、最大値 \(-4\)
→ 関数の値域と最大値・最小値
p.79 練習6\({\small (1)}~\)下に凸

\({\small (2)}~\)上に凸

\({\small (3)}~\)下に凸


\({\small (2)}~\)上に凸
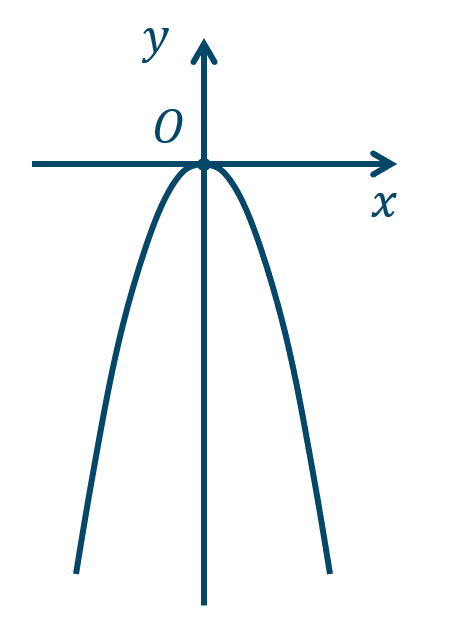
\({\small (3)}~\)下に凸
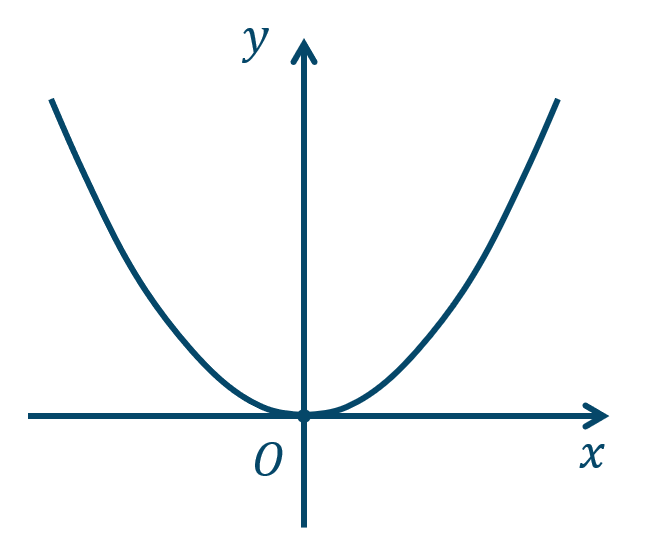
p.80 練習7\({\small (1)}~\)軸は \(y\) 軸、頂点 \((0,3)\)

\({\small (2)}~\)軸は \(y\) 軸、頂点 \((0,-1)\)

\({\small (3)}~\)軸は \(y\) 軸、頂点 \((0,2)\)

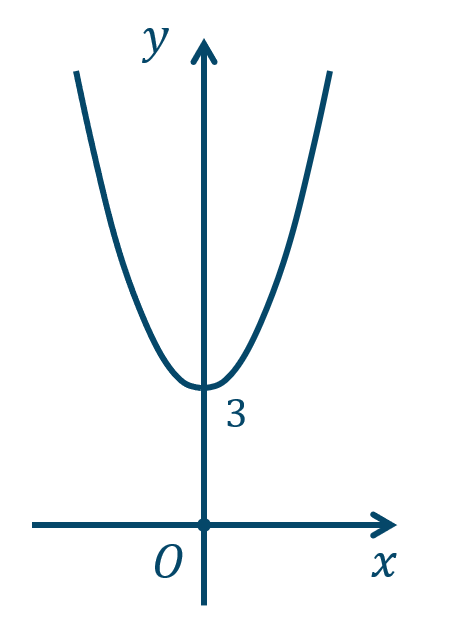
\({\small (2)}~\)軸は \(y\) 軸、頂点 \((0,-1)\)
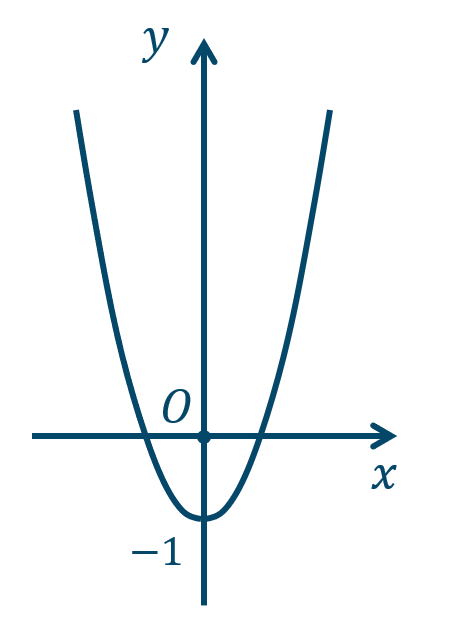
\({\small (3)}~\)軸は \(y\) 軸、頂点 \((0,2)\)
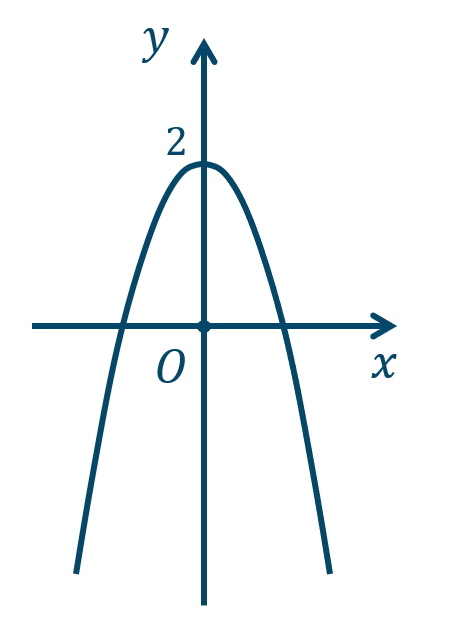
p.81 練習8\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,0)\)

\({\small (2)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)

\({\small (3)}~\)軸は \(x=-2\)、頂点 \((-2,0)\)

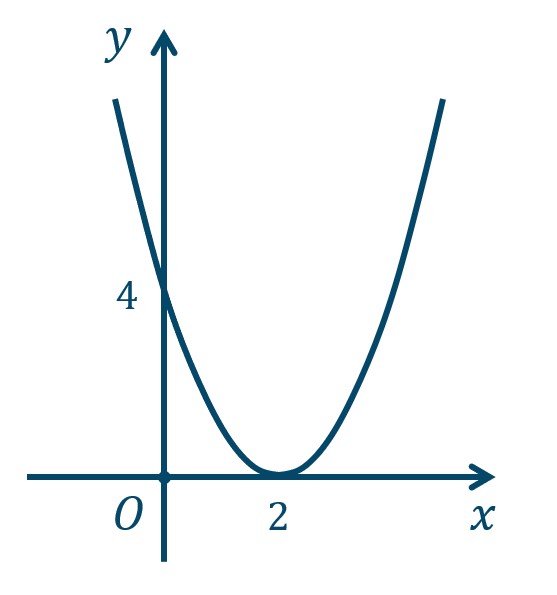
\({\small (2)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)
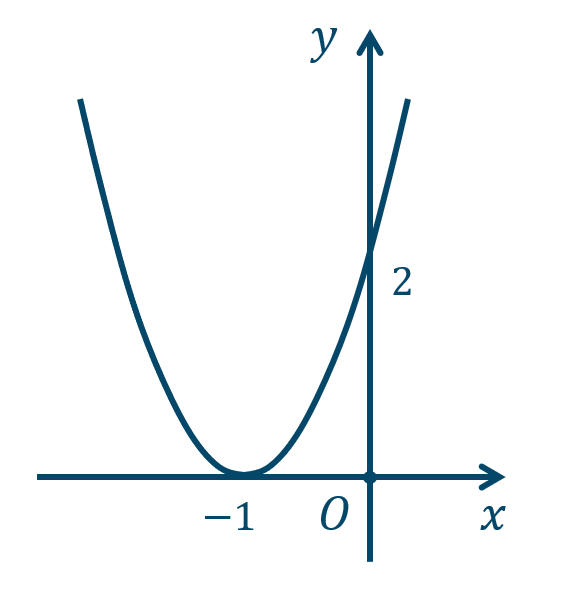
\({\small (3)}~\)軸は \(x=-2\)、頂点 \((-2,0)\)
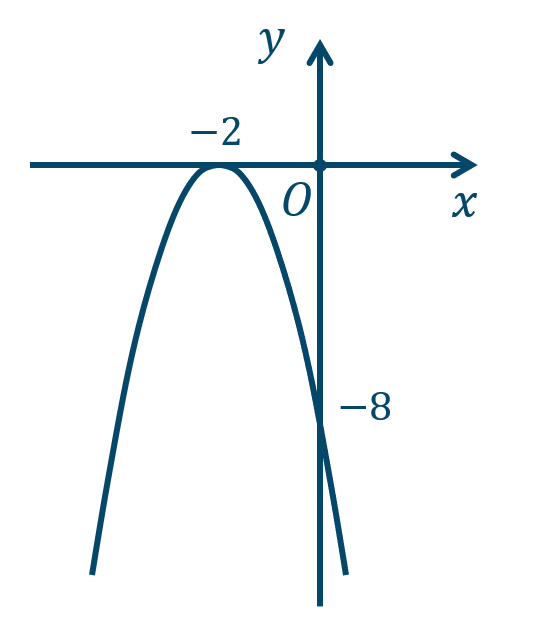
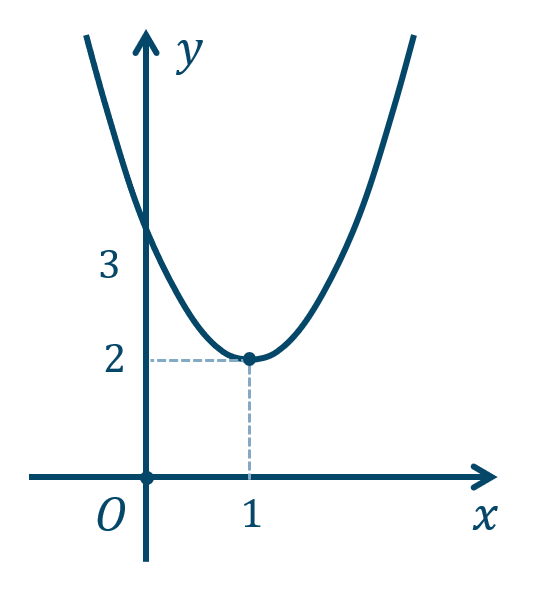
p.82 練習9\({\small (1)}~\)軸は \(x=1\)、頂点 \((1,2)\)

\({\small (2)}~\)軸は \(x=2\)、頂点 \((2,-4)\)

\({\small (3)}~\)軸は \(x=-1\)、頂点 \((-1,2)\)

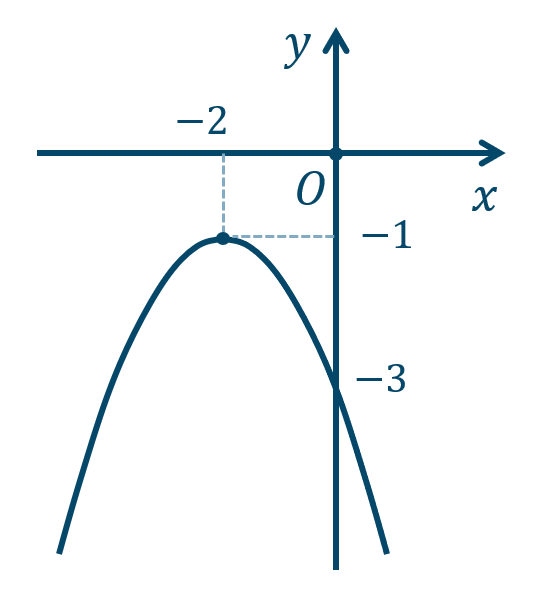
\({\small (4)}~\)軸は \(x=-2\)、頂点 \((-2,-1)\)

→ 2次関数のグラフ
\({\small (2)}~\)軸は \(x=2\)、頂点 \((2,-4)\)
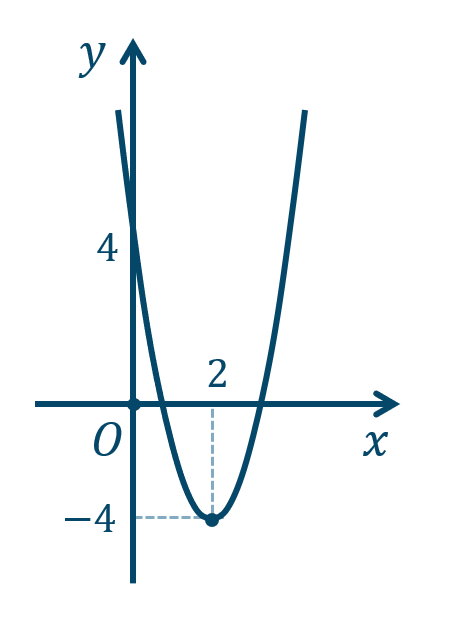
\({\small (3)}~\)軸は \(x=-1\)、頂点 \((-1,2)\)
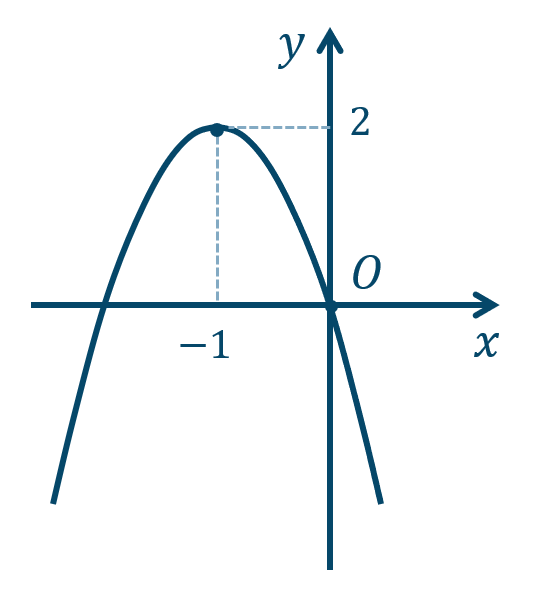
\({\small (4)}~\)軸は \(x=-2\)、頂点 \((-2,-1)\)
→ 2次関数のグラフ
p.83 練習10$${\small (1)}~(x+4)^2-16$$$${\small (2)}~(x-3)^2-1$$$${\small (3)}~2(x-2)^2-3$$$${\small (4)}~3(x+1)^2-1$$$${\small (5)}~\left(x+{ \frac{\,1\,}{\,2\,}}\right)^2-{ \frac{\,9\,}{\,4\,}}$$$${\small (6)}~-2\left(x-{ \frac{\,3\,}{\,2\,}}\right)^2+{ \frac{\,17\,}{\,2\,}}$$
p.84 練習11\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,-1)\)

\({\small (2)}~\)軸は \(x=-2\)、頂点 \((-2,-5)\)

\({\small (3)}~\)軸は \(x=1\)、頂点 \((1,4)\)

\({\small (4)}~\)軸は \(x=-{\large \frac{\,3\,}{\,2\,}}\)、頂点 \(\left(-{\large \frac{\,3\,}{\,2\,}},{\large \frac{\,9\,}{\,4\,}}\right)\)

→ 2次関数の平方完成
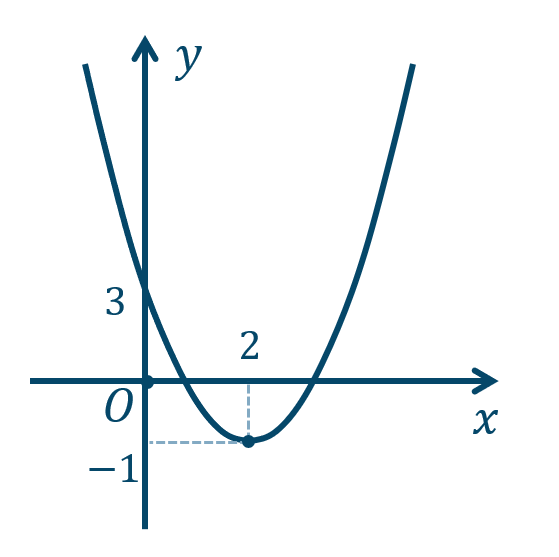
\({\small (2)}~\)軸は \(x=-2\)、頂点 \((-2,-5)\)
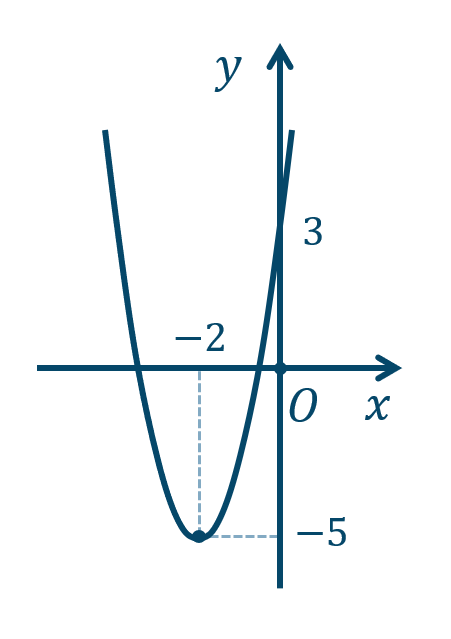
\({\small (3)}~\)軸は \(x=1\)、頂点 \((1,4)\)
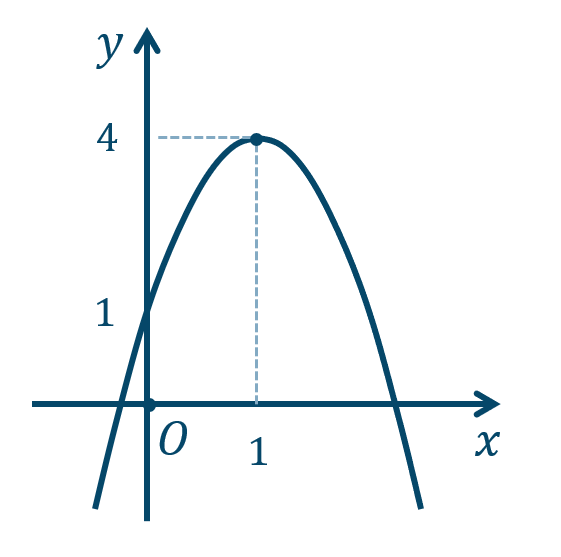
\({\small (4)}~\)軸は \(x=-{\large \frac{\,3\,}{\,2\,}}\)、頂点 \(\left(-{\large \frac{\,3\,}{\,2\,}},{\large \frac{\,9\,}{\,4\,}}\right)\)
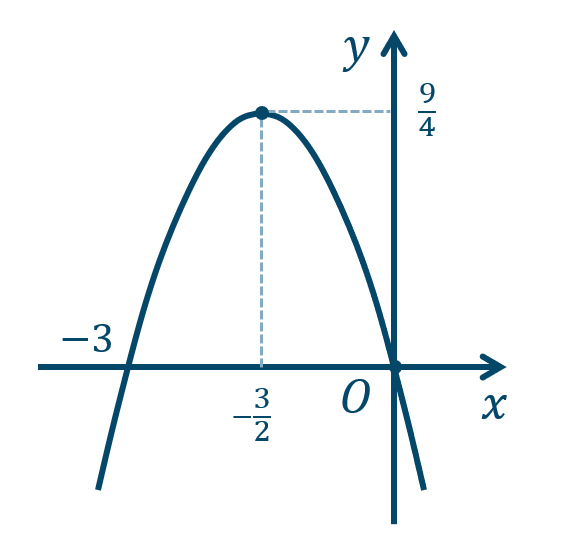
→ 2次関数の平方完成
p.84 深める$$~~~y=x^2-4x+9$$点 \((-1~,~-1)\) は通らない
p.86 研究 練習1$$~~~y=2x^2+3x+2$$→ 平行移動後のグラフ
p.88 問題 4\({\small (1)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)

\({\small (2)}~\)軸は \(x={\large \frac{\,1\,}{\,2\,}}\)、頂点 \(\left({\large \frac{\,1\,}{\,2\,}},1\right)\)

\({\small (3)}~\)軸は \(x=3\)、頂点 \((3,-4)\)

\({\small (4)}~\)軸は \(x=-{\large \frac{\,5\,}{\,4\,}}\)、頂点 \(\left(-{\large \frac{\,5\,}{\,4\,}},-{\large \frac{\,49\,}{\,8\,}}\right)\)

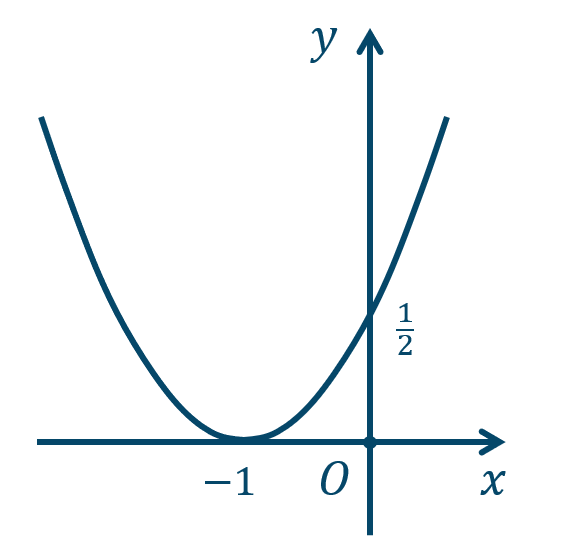
\({\small (2)}~\)軸は \(x={\large \frac{\,1\,}{\,2\,}}\)、頂点 \(\left({\large \frac{\,1\,}{\,2\,}},1\right)\)
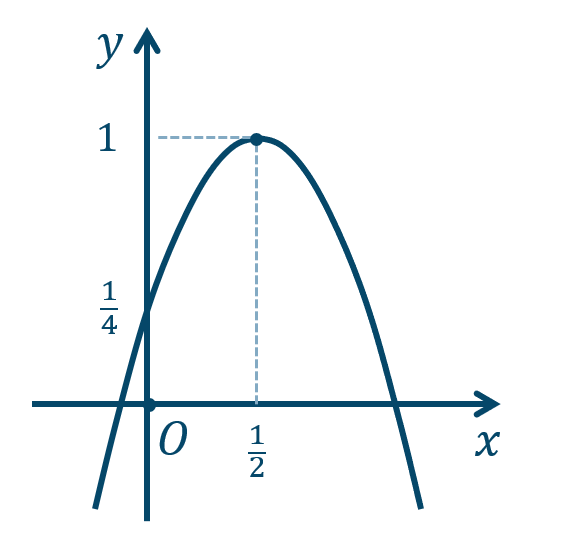
\({\small (3)}~\)軸は \(x=3\)、頂点 \((3,-4)\)
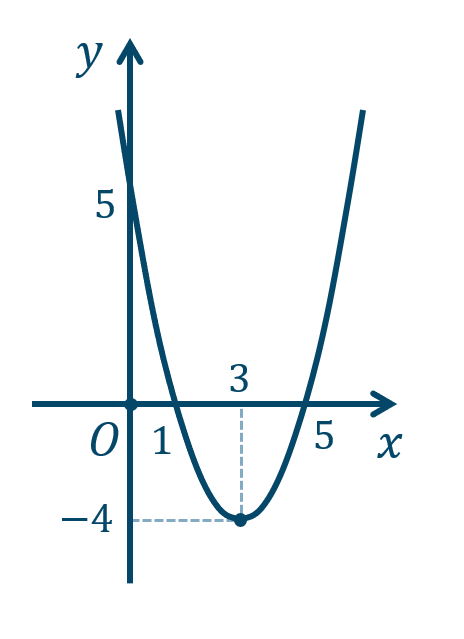
\({\small (4)}~\)軸は \(x=-{\large \frac{\,5\,}{\,4\,}}\)、頂点 \(\left(-{\large \frac{\,5\,}{\,4\,}},-{\large \frac{\,49\,}{\,8\,}}\right)\)
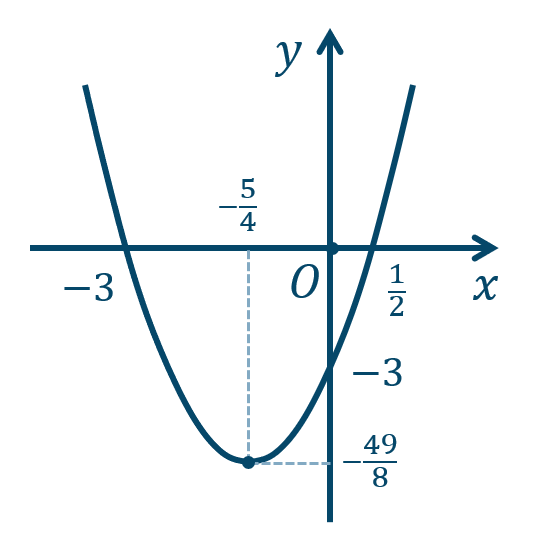
第2節 2次関数の値の変化
p.89 練習13\({\small (1)}~\)最大値なし
\(~~~~~\)最小値 \(4~(x=3)\)
\({\small (2)}~\)最大値 \(-3~(x=-1)\)
\(~~~~~\)最小値なし
\(~~~~~\)最小値 \(4~(x=3)\)
\({\small (2)}~\)最大値 \(-3~(x=-1)\)
\(~~~~~\)最小値なし
p.90 練習14\({\small (1)}~\)最大値なし
\(~~~~~\)最小値 \(-4~(x=3)\)
\({\small (2)}~\)最大値 \({\large \frac{\,25\,}{\,8\,}}~\left(x={\large \frac{\,5\,}{\,4\,}}\right)\)
\(~~~~~\)最小値なし
\(~~~~~\)最小値 \(-4~(x=3)\)
\({\small (2)}~\)最大値 \({\large \frac{\,25\,}{\,8\,}}~\left(x={\large \frac{\,5\,}{\,4\,}}\right)\)
\(~~~~~\)最小値なし
p.90 深める$$~~~y=x^2+2x+1$$
p.91 練習15\({\small (1)}~\)最大値 \(11~(x=2)\)
\(~~~~~\)最小値 \(2~(x=-1)\)
\({\small (2)}~\)最大値 \(1~(x=2)\)
\(~~~~~\)最小値 \(-3~(x=0)\)
\({\small (3)}~\)最大値 \(44~(x=3)\)
\(~~~~~\)最小値 \(8~(x=1)\)
\({\small (4)}~\)最大値 \(18~(x=3)\)
\(~~~~~\)最小値 \(0~(x=0,6)\)
→ 2次関数の最大値・最小値
\(~~~~~\)最小値 \(2~(x=-1)\)
\({\small (2)}~\)最大値 \(1~(x=2)\)
\(~~~~~\)最小値 \(-3~(x=0)\)
\({\small (3)}~\)最大値 \(44~(x=3)\)
\(~~~~~\)最小値 \(8~(x=1)\)
\({\small (4)}~\)最大値 \(18~(x=3)\)
\(~~~~~\)最小値 \(0~(x=0,6)\)
→ 2次関数の最大値・最小値
p.92 練習16$${\small (1)}~-3$$$${\small (2)}~-12$$→ 2次関数の決定③(最大値・最小値)
p.93 練習17\(0<a<1\) のとき
\(x=a\) で最大値 \(-a^2+2a+1\)
\(1≦a\) のとき
\(x=1\) で最大値 \(2\)
→ 定義域が変化する2次関数の最大値・最小値
\(x=a\) で最大値 \(-a^2+2a+1\)
\(1≦a\) のとき
\(x=1\) で最大値 \(2\)
→ 定義域が変化する2次関数の最大値・最小値
p.94 練習18\(a<0\) のとき
\(x=0\) で最小値 \(2a^2\)
\(0≦a≦1\) のとき
\(x=a\) で最小値 \(0\)
\(1<a\) のとき
\(x=1\) で最小値 \(2a^2-4a+2\)
→ 文字係数を含む2次関数の最大値・最小値
\(x=0\) で最小値 \(2a^2\)
\(0≦a≦1\) のとき
\(x=a\) で最小値 \(0\)
\(1<a\) のとき
\(x=1\) で最小値 \(2a^2-4a+2\)
→ 文字係数を含む2次関数の最大値・最小値
p.95 練習19$$~~~{ \frac{\,49\,}{\,2\,}}~(x=7)$$→ 最大値・最小値の文章問題
p.96 練習20$${\small (1)}~y=-{ \frac{\,1\,}{\,2\,}}(x+2)^2+4$$$${\small (2)}~y=2(x-2)^2-13$$→ 2次関数の決定①(頂点)
p.98 練習21$${\small (1)}~a=2~,~b=-6~,~c=4$$$${\small (2)}~x=3~,~y=2~,~z=1$$
p.98 練習22$$~~~y=2x^2-3x-4$$→ 2次関数の決定②(3点を通る)
第3節 2次方程式と2次不等式
p.100 練習23$${\small (1)}~x=0~,~-4$$$${\small (2)}~x=2~,~3$$$${\small (3)}~x=-1~,~-{ \frac{\,1\,}{\,2\,}}$$$${\small (4)}~x=2~,~-{ \frac{\,2\,}{\,3\,}}$$
p.101 練習24$${\small (1)}~x={ \frac{\,-7\pm\sqrt{33}\,}{\,2\,}}$$$${\small (2)}~x={ \frac{\,-2\pm\sqrt{7}\,}{\,3\,}}$$$${\small (3)}~x=3~,~-{ \frac{\,1\,}{\,3\,}}$$$${\small (4)}~x=-{ \frac{\,3\,}{\,2\,}}$$
p.102 練習25$${\small (1)}~x=-1\pm\sqrt{3}$$$${\small (2)}~x={ \frac{\,2\pm\sqrt{10}\,}{\,3\,}}$$$${\small (3)}~x=-\sqrt{3}$$$${\small (4)}~x=\sqrt{3}\pm1$$→ 2次方程式の解
p.104 練習27$$~~~m>-4$$
p.106 練習29$${\small (1)}~(-1~,~0)~,~(3~,~0)$$$${\small (2)}~\left({ \frac{\,3+\sqrt{5}\,}{\,2\,}}~,~0\right)~,~\left({ \frac{\,3-\sqrt{5}\,}{\,2\,}}~,~0\right)$$$${\small (3)}~(-1~,~0)$$$${\small (4)}~(3~,~0)~,~\left(-{ \frac{\,1\,}{\,2\,}}~,~0\right)$$\({\small (3)}\) が \(x\) 軸と接する
→ 2次関数とx軸との交点
→ 2次関数とx軸との交点
p.108 練習30\({\small (1)}~\)0個
\({\small (2)}~\)2個
\({\small (3)}~\)1個
\({\small (2)}~\)2個
\({\small (3)}~\)1個
p.109 発展 練習1$${\small (1)}~(3~,~1)~,~(5~,~5)$$$${\small (2)}~(2~,~2)$$
p.110 発展 練習2$$~~~k=-4~,~(2~,~-2)$$→ 放物線と直線の交点
p.111 練習32$${\small (1)}~x<-2$$$${\small (2)}~x≧2$$
p.113 練習33$${\small (1)}~x<1~,~3<x$$$${\small (2)}~-2<x<5$$$${\small (3)}~-1≦x≦0$$$${\small (4)}~x≦-1~,~2≦x$$$${\small (5)}~x<-3~,~-2<x$$$${\small (6)}~-3≦x≦3$$→ 2次不等式の解①(因数分解)
p.114 練習34$${\small (1)}~x≦{ \frac{\,1\,}{\,2\,}}~,~2≦x$$$${\small (2)}~-{ \frac{\,3\,}{\,2\,}}<x<-1$$$${\small (3)}~-1-\sqrt{2}≦x≦-1+\sqrt{2}$$$${\small (4)}~x<-\sqrt{5}~,~\sqrt{5}<x$$
p.115 練習35$${\small (1)}~x<-{ \frac{\,1\,}{\,2\,}}~,~1<x$$$${\small (2)}~{ \frac{\,5-\sqrt{13}\,}{\,6\,}}≦x≦{ \frac{\,5+\sqrt{13}\,}{\,6\,}}$$→ 2次不等式の解③(解の公式)
p.115 練習36\({\small (1)}~x=2\) 以外のすべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x=-3\)
\({\small (4)}~\)すべての実数
→ 2次不等式の解②(x軸と接する)
\({\small (2)}~\)解なし
\({\small (3)}~x=-3\)
\({\small (4)}~\)すべての実数
→ 2次不等式の解②(x軸と接する)
p.116 練習37\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~\)解なし
\({\small (4)}~\)すべての実数
→ 2次不等式の解④(交点がない)
\({\small (2)}~\)解なし
\({\small (3)}~\)解なし
\({\small (4)}~\)すべての実数
→ 2次不等式の解④(交点がない)
p.117 練習38\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x={\large \frac{\,\sqrt{3}\,}{\,3\,}}\)
\({\small (4)}~-1-\sqrt{3}<x<-1+\sqrt{3}\)
\({\small (2)}~\)解なし
\({\small (3)}~x={\large \frac{\,\sqrt{3}\,}{\,3\,}}\)
\({\small (4)}~-1-\sqrt{3}<x<-1+\sqrt{3}\)
p.118 練習39$$~~~m≦-\sqrt{3}~,~\sqrt{3}≦m$$
p.118 深める2次方程式 \(ax^2+bx+c=0\) の判別式 \(D\) の符号によって、2次関数 \(y=ax^2+bx+c\) のグラフと \(x\) 軸との交点の個数がわかるから
p.119 練習40$$~~~-4<m<0$$→ 絶対不等式
p.119 練習41$${\small (1)}~3<x≦4$$$${\small (2)}~-2≦x<-1~,~0<x≦{ \frac{\,1\,}{\,3\,}}$$
p.120 練習42$${\small (1)}~-4≦x≦-2~,~-1≦x≦1$$$${\small (2)}~-2≦x<-1$$→ 連立2次不等式の解
p.121 練習44$$~~~m>3$$→ 2次方程式の解の符号
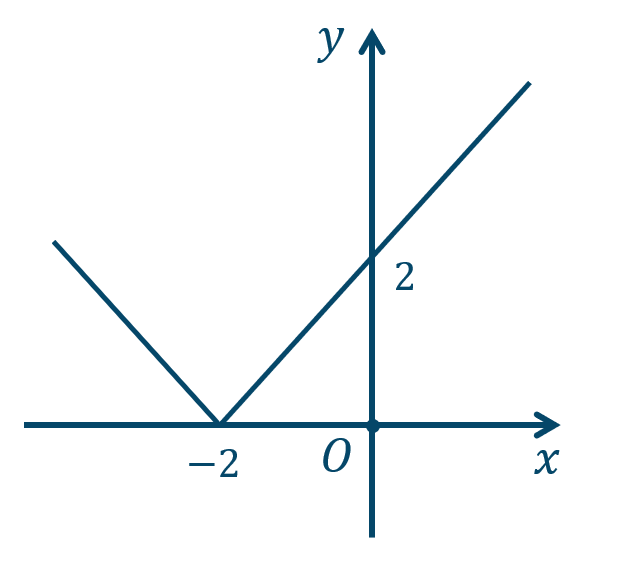
p.123 研究 練習1\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

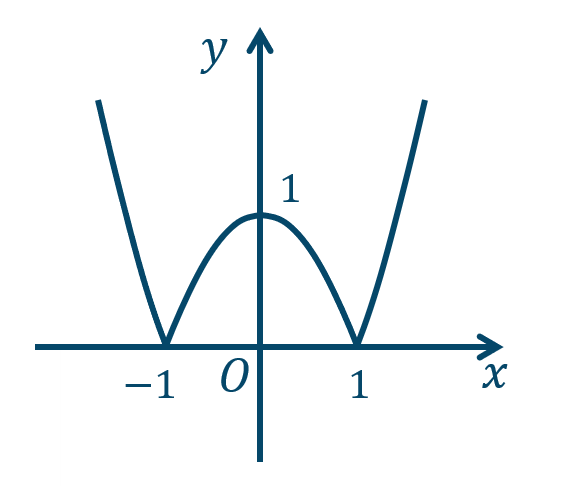
\({\small (2)}~\)
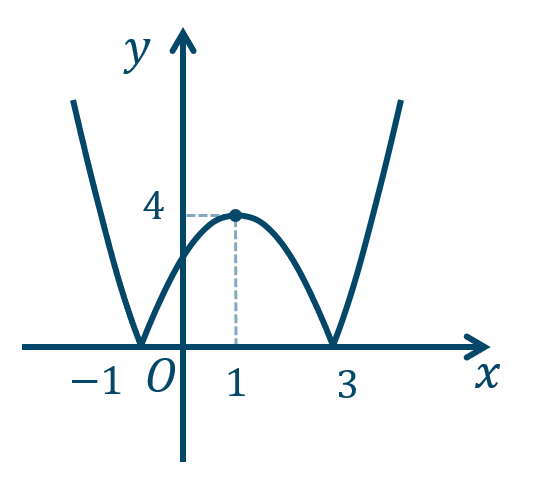
\({\small (3)}~\)
p.126 章末問題B 13[証明] 2次方程式$$~~~x^2-2mx+m-{ \frac{\,1\,}{\,2\,}}=0$$の判別式 \(D\) について、$$~~~D=4m^2-4m+2$$平方完成すると、$$~~~D=4\left(m-{ \frac{\,1\,}{\,2\,}}\right)^2+1$$これより、常に \(D>0\) となるので2次方程式は2つの解をもつ
よって、2次関数$$~~~y=x^2-2mx+m-{ \frac{\,1\,}{\,2\,}}$$は定数 \(m\) の値に関係なく常に \(x\) 軸と共有点をもつ [終]
よって、2次関数$$~~~y=x^2-2mx+m-{ \frac{\,1\,}{\,2\,}}$$は定数 \(m\) の値に関係なく常に \(x\) 軸と共有点をもつ [終]
次のページ「第4章 図形と計量」


