このページは、数研出版:高等学校数学C[709]
第3章 複素数平面
第3章 複素数平面

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
高等学校数学C 第1章 平面のベクトル
高等学校数学C 第2章 空間のベクトル
高等学校数学C 第3章 複素数平面
高等学校数学C 第4章 式と曲線
第3章 複素数平面
p.76 練習1

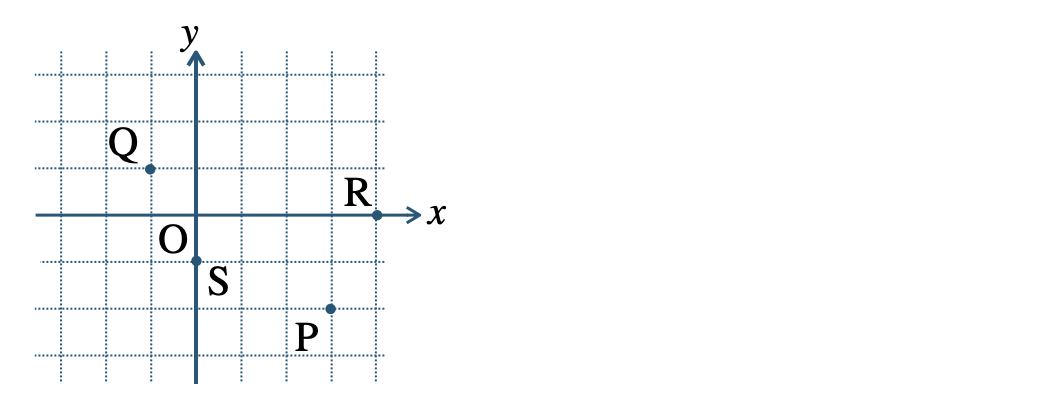
p.77 練習2 虚軸に関して対称
p.77 練習3$${\small (1)}~a=\frac{\,1\,}{\,2\,}(z+\overline {z})~,~b=\frac{\,1\,}{\,2i\,}(z-\overline {z})$$$${\small (2)}~$$性質1
[証明] \(z=a+bi\) が実数のとき、\(b=0\) であるので \({\small (1)}\) より、$$\begin{eqnarray}~~~\frac{\,1\,}{\,2i\,}(z-\overline {z})&=&0
\\[3pt]~~~z-\overline {z}&=&0
\\[2pt]~~~\overline {z}&=&z
\end{eqnarray}$$また、逆に \(\overline {z}=z\) のとき \({\small (1)}\) より、\(b=0\)
よって、\(z=a+bi\) は実数である
したがって、
\(z\) が実数 \(~\Leftrightarrow~\overline {z}=z\) [終]
性質2
[証明] \(z=a+bi\) が純虚数のとき、\(a=0~,~b\neq 0\) であるので \({\small (1)}\) より、$$\begin{eqnarray}~~~\frac{\,1\,}{\,2\,}(z+\overline {z})&=&0
\\[3pt]~~~z+\overline {z}&=&0
\\[2pt]~~~\overline {z}&=&-z
\end{eqnarray}$$また、逆に \(\overline {z}=-z\) で \(z\neq 0\) のとき \({\small (1)}\) より、\(a=0\)
また、\(z\neq 0\) のとき \(b\neq 0\)
よって、\(z=a+bi\) は純虚数である
したがって、
\(z\) が純虚数 \(~\Leftrightarrow~\overline {z}=-z\) ただし、 \(z\neq 0\) [終]
[証明] \(z=a+bi\) が実数のとき、\(b=0\) であるので \({\small (1)}\) より、$$\begin{eqnarray}~~~\frac{\,1\,}{\,2i\,}(z-\overline {z})&=&0
\\[3pt]~~~z-\overline {z}&=&0
\\[2pt]~~~\overline {z}&=&z
\end{eqnarray}$$また、逆に \(\overline {z}=z\) のとき \({\small (1)}\) より、\(b=0\)
よって、\(z=a+bi\) は実数である
したがって、
\(z\) が実数 \(~\Leftrightarrow~\overline {z}=z\) [終]
性質2
[証明] \(z=a+bi\) が純虚数のとき、\(a=0~,~b\neq 0\) であるので \({\small (1)}\) より、$$\begin{eqnarray}~~~\frac{\,1\,}{\,2\,}(z+\overline {z})&=&0
\\[3pt]~~~z+\overline {z}&=&0
\\[2pt]~~~\overline {z}&=&-z
\end{eqnarray}$$また、逆に \(\overline {z}=-z\) で \(z\neq 0\) のとき \({\small (1)}\) より、\(a=0\)
また、\(z\neq 0\) のとき \(b\neq 0\)
よって、\(z=a+bi\) は純虚数である
したがって、
\(z\) が純虚数 \(~\Leftrightarrow~\overline {z}=-z\) ただし、 \(z\neq 0\) [終]
p.78 練習4$${\small (1)}~\sqrt{13}$$$${\small (2)}~2\sqrt{5}$$$${\small (3)}~5$$$${\small (4)}~3$$
p.78 練習5[証明] \(z=a+bi\) とすると、\(-\overline {z}=-a+bi\)
よって、$$~~~|z|=\sqrt{a^2+b^2}$$$$\begin{eqnarray}~~~|-\overline {z}|&=&\sqrt{(-a)^2+b^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$したがって、$$~~~|-\overline {z}|=|z|$$[終]
よって、$$~~~|z|=\sqrt{a^2+b^2}$$$$\begin{eqnarray}~~~|-\overline {z}|&=&\sqrt{(-a)^2+b^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$したがって、$$~~~|-\overline {z}|=|z|$$[終]
p.79 練習6

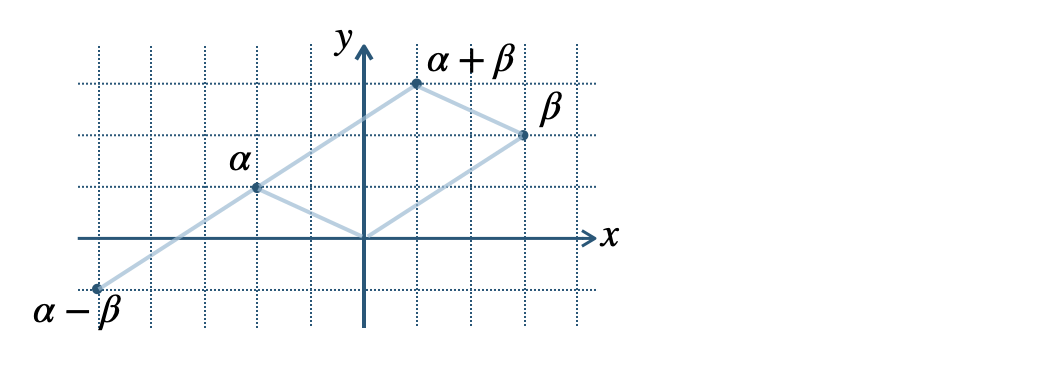
p.80 練習7$${\small (1)}~\sqrt{10}$$$${\small (2)}~2\sqrt{2}$$
p.81 練習8$$~~~y=-2$$
p.83 練習9$$~~~\overline {\alpha}+\overline {\beta}=i$$
p.83 練習10[証明] \(|\alpha|=1\) のとき、$$~~~\alpha \overline {\alpha}=|\alpha|^2=1~\Leftrightarrow~\overline {\alpha}=\frac{\,1\,}{\,\alpha\,}$$これより、$$\begin{eqnarray}~~~\alpha^2+\frac{\,1\,}{\,\alpha^2\,}&=&\alpha^2+(\overline {\alpha})^2
\\[3pt]~~~&=&\alpha^2+\overline {\alpha^2}\end{eqnarray}$$したがって、\(\alpha^2+\overline {\alpha^2}\) は実数であるから
\(\alpha^2+{\Large \frac{\,1\,}{\,\alpha^2\,}}\) も実数である [終]
\\[3pt]~~~&=&\alpha^2+\overline {\alpha^2}\end{eqnarray}$$したがって、\(\alpha^2+\overline {\alpha^2}\) は実数であるから
\(\alpha^2+{\Large \frac{\,1\,}{\,\alpha^2\,}}\) も実数である [終]
p.85 練習11$${\small (1)}~2\left( \cos{\frac{\,\pi\,}{\,6\,}}+i\sin{\frac{\,\pi\,}{\,6\,}} \right)$$$${\small (2)}~2\sqrt{2}\left( \cos{\frac{\,\pi\,}{\,4\,}}+i\sin{\frac{\,\pi\,}{\,4\,}} \right)$$$${\small (3)}~2\left\{ \cos{\left(-\frac{\,\pi\,}{\,3\,}\right)}+i\sin{\left(-\frac{\,\pi\,}{\,3\,}\right)} \right\}$$$${\small (4)}~\cos{\left(-\frac{\,\pi\,}{\,2\,}\right)}+i\sin{\left(-\frac{\,\pi\,}{\,2\,}\right)}$$
p.85 練習12[証明] \(\cos{(\theta+\pi)}=-\cos{\theta}\) と \(\sin{(\theta+\pi)}=-\sin{\theta}\) より、左辺は、$$\begin{split}&r\{ \cos{(\theta+\pi)}+i\sin{(\theta+\pi)} \}\\[2pt]~~=~&-r(\cos{\theta}+i\sin{\theta})\\[2pt]~~=~&-z\end{split}$$[終]
p.87 練習13$$~~~\alpha\beta=4\sqrt{2}\left( \cos{\frac{\,5\,}{\,12\,}\pi}+i\sin{\frac{\,5\,}{\,12\,}\pi} \right)$$$$~~~\frac{\,\alpha\,}{\,\beta\,}=\sqrt{2}\left( \cos{\frac{\,\pi\,}{\,12\,}}+i\sin{\frac{\,\pi\,}{\,12\,}} \right)$$
p.87 練習14$${\small (1)}~6$$$${\small (2)}~8$$$${\small (3)}~\frac{\,2\,}{\,3\,}$$$${\small (4)}~\frac{\,3\,}{\,4\,}$$
p.88 練習15\({\small (1)}~\)原点を中心に \({\Large \frac{\,\pi\,}{\,3\,}}\) 回転し、
原点からの距離を \(2\) 倍した点
\({\small (2)}~\)原点を中心に \({\Large \frac{\,3\,}{\,4\,}}\pi\) 回転し、
原点からの距離を \(\sqrt{2}\) 倍した点
\({\small (3)}~\)原点を中心に \({\Large \frac{\,\pi\,}{\,2\,}}\) 回転し、
原点からの距離を \(2\) 倍した点
原点からの距離を \(2\) 倍した点
\({\small (2)}~\)原点を中心に \({\Large \frac{\,3\,}{\,4\,}}\pi\) 回転し、
原点からの距離を \(\sqrt{2}\) 倍した点
\({\small (3)}~\)原点を中心に \({\Large \frac{\,\pi\,}{\,2\,}}\) 回転し、
原点からの距離を \(2\) 倍した点
p.89 練習16$${\small (1)}~(2\sqrt{3}+1)+(-\sqrt{3}+2)i$$$${\small (2)}~(-2+\sqrt{3})+(1+2\sqrt{3})i$$$${\small (3)}~-2-4i$$$${\small (4)}~(2-\sqrt{3})-(1+2\sqrt{3})i$$
p.89 練習17$$~~~\beta=(1-\sqrt{3})+(1+\sqrt{3})i$$$$~~~\beta=(1+\sqrt{3})+(1-\sqrt{3})i$$
p.91 練習18$${\small (1)}~16-16\sqrt{3}i$$$${\small (2)}~16$$$${\small (3)}~\frac{\,1\,}{\,64\,}$$
p.92 練習19$$~~~\pm1~,~\pm i$$$$~~~\frac{\,\sqrt{2}\,}{\,2\,}+\frac{\,\sqrt{2}\,}{\,2\,}i~,~\frac{\,\sqrt{2}\,}{\,2\,}-\frac{\,\sqrt{2}\,}{\,2\,}i$$$$~~~-\frac{\,\sqrt{2}\,}{\,2\,}+\frac{\,\sqrt{2}\,}{\,2\,}i~,~-\frac{\,\sqrt{2}\,}{\,2\,}-\frac{\,\sqrt{2}\,}{\,2\,}i$$
p.93 練習20$${\small (1)}~z=\frac{\,\sqrt{2}\,}{\,2\,}+\frac{\,\sqrt{2}\,}{\,2\,}i~,~-\frac{\,\sqrt{2}\,}{\,2\,}-\frac{\,\sqrt{2}\,}{\,2\,}i$$$${\small (2)}~z=1+i~,~-1+i~,~1-i~,~-1-i$$$${\small (3)}~z=\frac{\,\sqrt{6}\,}{\,2\,}+\frac{\,\sqrt{2}\,}{\,2\,}i~,~-\frac{\,\sqrt{6}\,}{\,2\,}-\frac{\,\sqrt{2}\,}{\,2\,}i$$
p.94 練習21$${\small (1)}~3+3i$$$${\small (2)}~4+2i$$$${\small (3)}~19-13i$$
p.95 練習22[証明] 頂点を \({\rm A}(\alpha)~,~{\rm B}(\beta)~,~{\rm C}(\gamma)\) とすると、線分 \({\rm BC}\) の中点は、$$~~~\frac{\,\beta+\gamma\,}{\,2\,}$$また、重心 \(\delta\) は線分 \({\rm BC}\) を \(2:1\) に内分するので、$$~~~\delta=\frac{\,\alpha+2\frac{\,\beta+\gamma\,}{\,2\,}\,}{\,2+1\,}=\frac{\,\alpha+\beta+\gamma\,}{\,3\,}$$[終]
p.95 練習23\({\small (1)}~\)原点が中心の半径 \(2\) の円
\({\small (2)}~\)点 \(1+i\) が中心の半径 \(1\) の円
\({\small (3)}~\)2点 \({\rm A}(2)~,~{\rm B}(4i)\) を結ぶ線分 \({\rm AB}\) の垂直二等分線
\({\small (2)}~\)点 \(1+i\) が中心の半径 \(1\) の円
\({\small (3)}~\)2点 \({\rm A}(2)~,~{\rm B}(4i)\) を結ぶ線分 \({\rm AB}\) の垂直二等分線
p.96 練習24 点 \(4\) が中心の半径 \(2\) の円
p.97 練習25 点 \(-2i\) が中心の半径 \(1\) の円
p.98 練習26$$~~~\gamma=2\sqrt{3}+(\sqrt{3}+3)i$$
p.99 練習27$$~~~\frac{\,\pi\,}{\,4\,}$$
p.100 練習28$${\small (1)}~x=0$$$${\small (2)}~x=-5$$
p.101 練習29$${\small (1)}~i$$$${\small (2)}~\angle{\rm A}=\frac{\,\pi\,}{\,2\,}~,~\angle{\rm B}=\frac{\,\pi\,}{\,4\,}~,~\angle{\rm C}=\frac{\,\pi\,}{\,4\,}$$
p.102 研究 練習1 正三角形
問題
p.103 問題2[証明] $$\begin{eqnarray}~~~\overline {\alpha\overline {\beta}+\overline {\alpha}\beta}&=&\overline {\alpha\overline {\beta}}+\overline {\overline {\alpha}\beta}\\[2pt]~~~&=&\overline {\alpha}\beta+\alpha\overline {\beta}\\[2pt]~~~&=&\alpha\overline {\beta}+\overline {\alpha}\beta\end{eqnarray}$$[終]
p.103 問題6[証明] ド・モアブルの定理より、\(k=1~,~2~,~3~,~\cdots n-1\) に対して、$$\begin{eqnarray}~~~\alpha ^k&=&\left( \cos{\frac{\,2\pi\,}{\,n\,}}+i\sin{\frac{\,2\pi\,}{\,n\,}} \right)^k\\[3pt]~~~&=&\cos{\frac{\,2k\pi\,}{\,n\,}}+i\sin{\frac{\,2k\pi\,}{\,n\,}}\end{eqnarray}$$これより、\(k=1~,~2~,~3~,~\cdots n-1\) のとき、\(1\) の \(n\)乗根 \(z_k\) について \(z_k=\alpha ^k\)
したがって、\(1\) の \(n\)乗根は
\(1~,~\alpha~,~\alpha^2~,~\alpha^3~,~\cdots~,~\alpha^{n-1}\)
である [終]
したがって、\(1\) の \(n\)乗根は
\(1~,~\alpha~,~\alpha^2~,~\alpha^3~,~\cdots~,~\alpha^{n-1}\)
である [終]
p.103 問題10$${\small (1)}~\gamma=-\beta$$\({\small (2)}~\)[証明] \(\gamma=-\beta\) より、$$\begin{split}&{\rm AB^2+AC^2}
\\[2pt]~~=~&|\beta-\alpha|^2+|\gamma-\alpha|^2
\\[2pt]~~~=&|\beta-\alpha|^2+|\beta+\alpha|^2
\\[2pt]~~~=&(\beta-\alpha)(\overline {\beta}-\overline {\alpha})+(\beta+\alpha)(\overline {\beta}+\overline {\alpha})
\\[2pt]~~~=&2\alpha\overline {\alpha}+2\beta\overline {\beta}
\\[2pt]~~~=&2(|\alpha|^2+|\beta|^2)
\end{split}$$また、$$\begin{eqnarray}~~~2({\rm AM^2+BM^2})&=&2(|0-\alpha|^2+|0-\beta|^2)
\\[2pt]~~~&=&2(|\alpha|^2+|\beta|^2)
\end{eqnarray}$$したがって、$$~~~{\rm AB^2+AC^2}=2({\rm AM^2+BM^2})$$[終]
\\[2pt]~~=~&|\beta-\alpha|^2+|\gamma-\alpha|^2
\\[2pt]~~~=&|\beta-\alpha|^2+|\beta+\alpha|^2
\\[2pt]~~~=&(\beta-\alpha)(\overline {\beta}-\overline {\alpha})+(\beta+\alpha)(\overline {\beta}+\overline {\alpha})
\\[2pt]~~~=&2\alpha\overline {\alpha}+2\beta\overline {\beta}
\\[2pt]~~~=&2(|\alpha|^2+|\beta|^2)
\end{split}$$また、$$\begin{eqnarray}~~~2({\rm AM^2+BM^2})&=&2(|0-\alpha|^2+|0-\beta|^2)
\\[2pt]~~~&=&2(|\alpha|^2+|\beta|^2)
\end{eqnarray}$$したがって、$$~~~{\rm AB^2+AC^2}=2({\rm AM^2+BM^2})$$[終]
章末問題
p.104 章末問題B 6\({\small (1)}~\)[証明] \(|z|=|z-\alpha|\) より、$$\begin{eqnarray}~~~|z|^2&=&|z-\alpha|^2
\\[2pt]~~~z\overline {z}&=&(z-\alpha)(\overline {z}-\overline {\alpha})
\\[2pt]~~~z\overline {z}&=&z\overline {z}-\overline {\alpha}z-\alpha\overline {z}+\alpha\overline {\alpha}
\\[2pt]~~~\overline {\alpha}z+\alpha\overline {z}&=&\alpha\overline {\alpha}=|\alpha|^2
\end{eqnarray}$$したがって、\(\overline {\alpha}z+\alpha\overline {z}\) の値は一定 [終]
$${\small (2)}~\overline {\alpha}z+\alpha\overline {z}=4$$
\\[2pt]~~~z\overline {z}&=&(z-\alpha)(\overline {z}-\overline {\alpha})
\\[2pt]~~~z\overline {z}&=&z\overline {z}-\overline {\alpha}z-\alpha\overline {z}+\alpha\overline {\alpha}
\\[2pt]~~~\overline {\alpha}z+\alpha\overline {z}&=&\alpha\overline {\alpha}=|\alpha|^2
\end{eqnarray}$$したがって、\(\overline {\alpha}z+\alpha\overline {z}\) の値は一定 [終]
$${\small (2)}~\overline {\alpha}z+\alpha\overline {z}=4$$
次のページ「第4章 式と曲線」


