このページは、数研出版:数学Ⅱ[709]
第3章 図形と方程式
第3章 図形と方程式

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版数学Ⅱ 第1章 式と証明
数研出版数学Ⅱ 第2章 複素数と方程式
数研出版数学Ⅱ 第3章 図形と方程式
数研出版数学Ⅱ 第4章 三角関数
数研出版数学Ⅱ 第5章 指数関数と対数関数
数研出版数学Ⅱ 第6章 微分法と積分法
第3章 図形と方程式
第1節 点と直線
p.72 練習1$${\small (1)}~6$$$${\small (2)}~3$$$${\small (3)}~3$$
p.73 深める\(a> b\) のとき、\(b<x<a\) であるから、
\({\rm AP}=a-x~,~{\rm PB}=x-b\)
\({\rm AP:PB}=m:n\) より、$$\begin{eqnarray}~~~a-x:x-b&=&m:n\\[2pt]~~~n(a-x)&=&m(x-b)\\[2pt]~~~(m+n)x&=&na+mb\\[3pt]~~~x&=&\frac{\,na+mb\,}{\,m+n\,}\end{eqnarray}$$
\({\rm AP}=a-x~,~{\rm PB}=x-b\)
\({\rm AP:PB}=m:n\) より、$$\begin{eqnarray}~~~a-x:x-b&=&m:n\\[2pt]~~~n(a-x)&=&m(x-b)\\[2pt]~~~(m+n)x&=&na+mb\\[3pt]~~~x&=&\frac{\,na+mb\,}{\,m+n\,}\end{eqnarray}$$
p.74 問1$${\small (1)}~4$$$${\small (2)}~2$$$${\small (3)}~7$$$${\small (4)}~-1$$
p.74 練習2$${\small (1)}~{ \frac{\,14\,}{\,5\,}}$$$${\small (2)}~22$$$${\small (3)}~-18$$$${\small (4)}~2$$→ 直線上の線分の長さ・内分点・外分点
p.75 練習3$${\small (1)}~5$$$${\small (2)}~5\sqrt{2}$$→ 平面上の線分の長さ
p.76 練習4[証明]
2点間の距離の公式より、
\({\rm AB}^2=3^2+(-1)^2=10\)
\({\rm BC}^2=(-2)^2+4)^2=20\)
\({\rm CA}^2=(-1)^2+(-3)^2=10\)
これより、
\({\rm BC^2=AB^2+CA^2}\) と \({\rm AB=CA}\)
が成り立つ
したがって、\(\triangle {\rm ABC}\) は辺 \({\rm BC}\) を斜辺とする直角二等辺三角形となる [終]
→ 平面上の三角形の形状
2点間の距離の公式より、
\({\rm AB}^2=3^2+(-1)^2=10\)
\({\rm BC}^2=(-2)^2+4)^2=20\)
\({\rm CA}^2=(-1)^2+(-3)^2=10\)
これより、
\({\rm BC^2=AB^2+CA^2}\) と \({\rm AB=CA}\)
が成り立つ
したがって、\(\triangle {\rm ABC}\) は辺 \({\rm BC}\) を斜辺とする直角二等辺三角形となる [終]
→ 平面上の三角形の形状
p.76 練習5[証明] 座標平面上に4点 \({\rm A~,~B~,~C~,~D}\) を次のようにとると、
\({\rm A}(a~,~b)\) \({\rm B}(-c~,~0)\)
\({\rm C}(2c~,~0)\) \({\rm D}(0~,~0)\)
このとき、
\({\rm AB}^2=(-c-a)^2+(-b)^2\)
\(=a^2+b^2+c^2+2ca\)
\({\rm AC}^2=(2c-a)^2+(-b)^2\)
\(=a^2+b^2+4c^2-4ca\)
よって、
\(2{\rm AB}^2+{\rm AC}^2\)
\(=3(a^2+b^2+2c^2)\)
また、
\({\rm AD}^2=a^2+b^2\)
\({\rm BD}^2=(-c)^2=c^2\)
よって、
\({\rm AD}^2+2{\rm BD}^2\)
\(=a^2+b^2+2c^2\)
したがって、
\(2{\rm AB}^2+{\rm AC}^2=3({\rm AD}^2+2{\rm BD}^2)\) [終]
→ 座標を利用した等式の証明
\({\rm A}(a~,~b)\) \({\rm B}(-c~,~0)\)
\({\rm C}(2c~,~0)\) \({\rm D}(0~,~0)\)
このとき、
\({\rm AB}^2=(-c-a)^2+(-b)^2\)
\(=a^2+b^2+c^2+2ca\)
\({\rm AC}^2=(2c-a)^2+(-b)^2\)
\(=a^2+b^2+4c^2-4ca\)
よって、
\(2{\rm AB}^2+{\rm AC}^2\)
\(=3(a^2+b^2+2c^2)\)
また、
\({\rm AD}^2=a^2+b^2\)
\({\rm BD}^2=(-c)^2=c^2\)
よって、
\({\rm AD}^2+2{\rm BD}^2\)
\(=a^2+b^2+2c^2\)
したがって、
\(2{\rm AB}^2+{\rm AC}^2=3({\rm AD}^2+2{\rm BD}^2)\) [終]
→ 座標を利用した等式の証明
p.78 練習6$${\small (1)}~{\rm C}\left(-{ \frac{\,3\,}{\,5\,}}~,~-{ \frac{\,4\,}{\,5\,}}\right)$$$${\small (2)}~{\rm D}(9~,~-20)$$$${\small (3)}~{\rm E}(-11~,~20)$$$${\small (4)}~{\rm M}(-1~,~0)$$
p.79 練習7$${\small (1)}~(2~,~1)$$$${\small (2)}~\left(-3~,~-{ \frac{\,5\,}{\,3\,}}\right)$$→ 平面上の内分点・外分点・重心
p.79 練習8$$~~~(8~,~-3)$$→ 点に対して対称な点
p.80 練習9\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

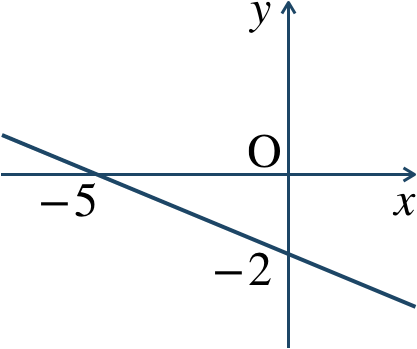
\({\small (2)}~\)
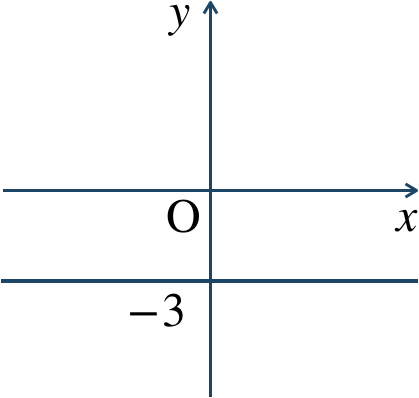
\({\small (3)}~\)
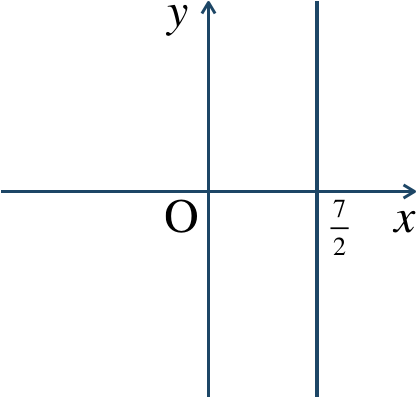
p.81 練習10$${\small (1)}~y=2x-1$$$${\small (2)}~y=-{ \frac{\,2\,}{\,3\,}}x-{ \frac{\,11\,}{\,3\,}}$$$${\small (3)}~x=2$$→ 直線の方程式
p.82 練習11$${\small (1)}~y=-2x+11$$$${\small (2)}~y=x+3$$$${\small (3)}~y=-1$$$${\small (4)}~x=-3$$→ 2点を通る直線の方程式
p.82 練習12[証明] 2点 \((a~,~0)~,~(0~,~b)\) を通る直線であるので、
\(y-0={\large \frac{\,b-0\,}{\,0-a\,}}(x-a)\)
これより、
\(y=-{\large \frac{\,b\,}{\,a\,}}x+b\)
移項すると、
\({\large \frac{\,bx\,}{\,a\,}}+y=b\)
両辺を \(b\) で割ると、
\({\large \frac{\,x\,}{\,a\,}}+{\large \frac{\,y\,}{\,b\,}}=1\) [終]
\(y-0={\large \frac{\,b-0\,}{\,0-a\,}}(x-a)\)
これより、
\(y=-{\large \frac{\,b\,}{\,a\,}}x+b\)
移項すると、
\({\large \frac{\,bx\,}{\,a\,}}+y=b\)
両辺を \(b\) で割ると、
\({\large \frac{\,x\,}{\,a\,}}+{\large \frac{\,y\,}{\,b\,}}=1\) [終]
p.84 練習13\({\small (1)}~\)垂直
\({\small (2)}~\)平行
\({\small (2)}~\)平行
p.85 問2解をもたない \(a=2~,~c\neq3\)
無数の解をもつ \(a=2~,~c=3\)
無数の解をもつ \(a=2~,~c=3\)
p.85 練習15ただ1組の解をもつ \(a\neq -{\large \frac{\,2\,}{\,3\,}}\)
解をもたない \(a=-{\large \frac{\,2\,}{\,3\,}},~c\neq{\large \frac{\,4\,}{\,3\,}}\)
無数の解をもつ \(a=-{\large \frac{\,2\,}{\,3\,}},~c={\large \frac{\,4\,}{\,3\,}}\)
解をもたない \(a=-{\large \frac{\,2\,}{\,3\,}},~c\neq{\large \frac{\,4\,}{\,3\,}}\)
無数の解をもつ \(a=-{\large \frac{\,2\,}{\,3\,}},~c={\large \frac{\,4\,}{\,3\,}}\)
p.86 練習16$$~~~x-3y-4=0$$→ 2直線の交点を通る直線
p.86 深める同じではない
①’は、2直線の交点を通る直線を表すが、直線 \(2x-y-3=0\) は表すことができない
①’は、2直線の交点を通る直線を表すが、直線 \(2x-y-3=0\) は表すことができない
p.87 練習17$${\small (1)}~(1~,~3)$$$${\small (2)}~(1~,~4)$$→ 直線に対して対称な点
p.89 練習18$${\small (1)}~\sqrt{5}$$$${\small (2)}~1$$$${\small (3)}~{ \frac{\,2\sqrt{5}\,}{\,5\,}}$$$${\small (4)}~{ \frac{\,\sqrt{10}\,}{\,2\,}}$$→ 点と直線との距離
p.90 練習19[証明] 座標平面上に3点を
\({\rm A}(a~,~b)~,~{\rm B}(-c~,~0)~,~{\rm C}(c~,~0)\)
とすると、
直線 \({\rm AB}\) の傾きが \({\large \frac{\,b\,}{\,a+c\,}}\) で、辺 \({\rm AB}\) の中点が \(\left({\large \frac{\,a-c\,}{2}}~,~{\large \frac{\,b\,}{\,2\,}}\right)\) より、辺 \({\rm AB}\) の垂直二等分線の方程式は、$$~~~y-\frac{\,b\,}{\,2\,}=-\frac{\,a+c\,}{b}\left(x-\frac{\,a-c\,}{2}\right)$$$$~\Leftrightarrow~y=-\frac{\,a+c\,}{b}x+\frac{\,a^2+b^2-c^2\,}{2b}$$これを①とする
次に、直線 \({\rm AC}\) の傾きが \({\large \frac{b}{\,a-c\,}}\) で、辺 \({\rm AC}\) の中点が \(\left({\large \frac{\,a+c\,}{2}}~,~{\large \frac{\,b\,}{2}}\right)\) より、辺 \({\rm AC}\) の垂直二等分線の方程式は、$$~~~y-\frac{\,b\,}{2}=-\frac{\,a-c\,}{b}\left(x-\frac{\,a+c\,}{2}\right)$$$$~\Leftrightarrow~y=-\frac{\,a-c\,}{b}x+\frac{\,a^2+b^2-c^2\,}{2b}$$これを②とする
①と②を連立すると、交点は$$~~~\left(0~,~\frac{\,a^2+b^2-c^2\,}{2b}\right)$$これは、\(y\) 軸上のの点で辺 \({\rm BC}\) 上にある
したがって、三角形の3辺の垂直二等分線は、1点で交わる [終]
\({\rm A}(a~,~b)~,~{\rm B}(-c~,~0)~,~{\rm C}(c~,~0)\)
とすると、
直線 \({\rm AB}\) の傾きが \({\large \frac{\,b\,}{\,a+c\,}}\) で、辺 \({\rm AB}\) の中点が \(\left({\large \frac{\,a-c\,}{2}}~,~{\large \frac{\,b\,}{\,2\,}}\right)\) より、辺 \({\rm AB}\) の垂直二等分線の方程式は、$$~~~y-\frac{\,b\,}{\,2\,}=-\frac{\,a+c\,}{b}\left(x-\frac{\,a-c\,}{2}\right)$$$$~\Leftrightarrow~y=-\frac{\,a+c\,}{b}x+\frac{\,a^2+b^2-c^2\,}{2b}$$これを①とする
次に、直線 \({\rm AC}\) の傾きが \({\large \frac{b}{\,a-c\,}}\) で、辺 \({\rm AC}\) の中点が \(\left({\large \frac{\,a+c\,}{2}}~,~{\large \frac{\,b\,}{2}}\right)\) より、辺 \({\rm AC}\) の垂直二等分線の方程式は、$$~~~y-\frac{\,b\,}{2}=-\frac{\,a-c\,}{b}\left(x-\frac{\,a+c\,}{2}\right)$$$$~\Leftrightarrow~y=-\frac{\,a-c\,}{b}x+\frac{\,a^2+b^2-c^2\,}{2b}$$これを②とする
①と②を連立すると、交点は$$~~~\left(0~,~\frac{\,a^2+b^2-c^2\,}{2b}\right)$$これは、\(y\) 軸上のの点で辺 \({\rm BC}\) 上にある
したがって、三角形の3辺の垂直二等分線は、1点で交わる [終]
p.91 問題6\({\small (1)}~\)[証明]
それぞれの直線の傾きは、
\(-{\large \frac{\,a\,}{\,b\,}}~,~-{\large \frac{\,a’\,}{\,b’\,}}\)
これより、2直線が平行となるので、
\(-{\large \frac{\,a\,}{\,b\,}}=-{\large \frac{\,a’\,}{\,b’\,}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
また、2直線が垂直となるので、
\(\left(-{\large \frac{\,a\,}{\,b\,}}\right)\left(-{\large \frac{\,a’\,}{\,b’\,}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
[終]
\({\small (2)}~\)
平行 \(a=-{\large \frac{\,1\,}{\,3\,}}\)
垂直 \(a=1~,~-2\)
それぞれの直線の傾きは、
\(-{\large \frac{\,a\,}{\,b\,}}~,~-{\large \frac{\,a’\,}{\,b’\,}}\)
これより、2直線が平行となるので、
\(-{\large \frac{\,a\,}{\,b\,}}=-{\large \frac{\,a’\,}{\,b’\,}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
また、2直線が垂直となるので、
\(\left(-{\large \frac{\,a\,}{\,b\,}}\right)\left(-{\large \frac{\,a’\,}{\,b’\,}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
[終]
\({\small (2)}~\)
平行 \(a=-{\large \frac{\,1\,}{\,3\,}}\)
垂直 \(a=1~,~-2\)
第2節 円
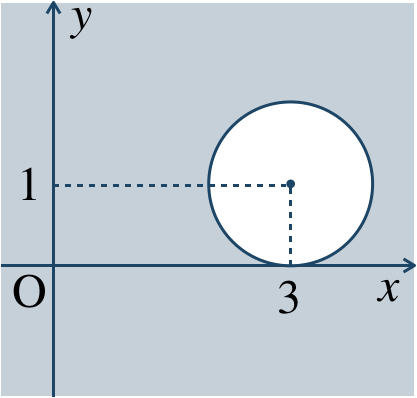
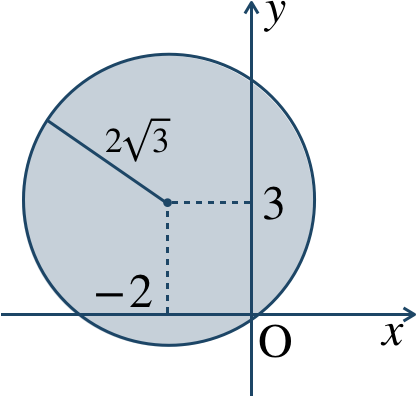
p.92 練習20$${\small (1)}~x^2+y^2=9$$$${\small (2)}~(x+2)^2+(y-3)^2=5$$
p.93 練習22$${\small (1)}~(x+1)^2+(y-2)^2=10$$$${\small (2)}~(x-1)^2+(y+2)^2=17$$→ 円の方程式の決定①(点の条件)
p.94 練習23\({\small (1)}~\)中心 \((1~,~-2)\)、半径 \(4\)
\({\small (2)}~\)中心 \((-3~,~4)\)、半径 \(3\)
\({\small (2)}~\)中心 \((-3~,~4)\)、半径 \(3\)
p.94 問3\({\small (1)}~\)点 \((-1~,~2)\)
\({\small (2)}~\)ない
\({\small (2)}~\)ない
p.95 練習25$${\small (1)}~x^2+y^2-2x+2y-3=0$$\({\small (2)}~\)外心 \((1~,~-1)\)、半径 \(\sqrt{5}\)
p.96 練習26$${\small (1)}~(3~,~4)~,~(-4~,~-3)$$$${\small (2)}~(1~,~1)$$→ 円と直線との共有点
p.98 問4$${\small (1)}~k=\sqrt{2}~,~\left(-{ \frac{\,\sqrt{2}\,}{\,2\,}}~,~{ \frac{\,\sqrt{2}\,}{\,2\,}}\right)$$$$~~~~~~k=-\sqrt{2}~,~\left({ \frac{\,\sqrt{2}\,}{\,2\,}}~,~-{ \frac{\,\sqrt{2}\,}{\,2\,}}\right)$$$${\small (2)}~k<-\sqrt{2}~,~\sqrt{2}<k$$
p.98 練習28$${\small (1)}~-5≦k≦5$$\({\small (2)}~\)\(k=5\) のとき \((-2,1)\)
\(k=-5\) のとき \((2,-1)\)
\(k=-5\) のとき \((2,-1)\)
p.99 練習29\(-2\sqrt{5}<k<2\sqrt{5}\) のとき2個
\(k=\pm2\sqrt{5}\) のとき1個
\(k<-2\sqrt{5}~,~2\sqrt{5}< k\) のとき0個
→ 円と直線との位置関係
\(k=\pm2\sqrt{5}\) のとき1個
\(k<-2\sqrt{5}~,~2\sqrt{5}< k\) のとき0個
→ 円と直線との位置関係
p.100 練習30$$~~~\frac{\,2\sqrt{5}\,}{\,5\,}$$
p.101 練習31$${\small (1)}~x-2y+10=0$$$${\small (2)}~2x+\sqrt{5}y+9=0$$
p.102 練習32$$~~~y=1~,~(0~,~1)$$$$~~~3x+4y+5=0~,~\left(-{ \frac{\,3\,}{\,5\,}}~,~-{ \frac{\,4\,}{\,5\,}}\right)$$→ 円の接線の方程式
p.102 深める点 \((1~,~3)\) を通り、傾き \(m\) の直線は、$$\begin{eqnarray}~~~y&=&m(x-1)+3\\[2pt]~~~y&=&mx-m+3\end{eqnarray}$$円の方程式と連立して、\(x\) の2次方程式の判別式 \(D=0\) を解く
p.104 練習34$$~~~(x-4)^2+(y-2)^2=45$$
p.104 深める\({\small (1)}~\)内接する
\({\small (2)}~\)内接する
\({\small (2)}~\)内接する
p.105 練習35$$~~~(1,3)~,~(3,-1)$$→ 2つの円の共有点の座標
p.106 練習36中心 \(\left(1~,~-{\large \frac{\,1\,}{\,2\,}}\right)\)、半径 \({\large \frac{\,5\,}{\,2\,}}\)
→ 2つの円の交点を通る円・直線
→ 2つの円の交点を通る円・直線
p.106 深める円 \(x^2+y^2=5\) は表すことができない
p.107 問題16\({\small (1)}~\)
① \(y=x\) 上の点 \((a~,~a)\) における垂線を引く
② 2点 \((0~,~1)~,~(a~,~a)\) を結ぶ線分の垂直二等分線を引く
③ ①と②の直線の交点を中心として、\((a~,~a)\) までの距離を半径とした円が円 \(C\) となる
① \(y=x\) 上の点 \((a~,~a)\) における垂線を引く
② 2点 \((0~,~1)~,~(a~,~a)\) を結ぶ線分の垂直二等分線を引く
③ ①と②の直線の交点を中心として、\((a~,~a)\) までの距離を半径とした円が円 \(C\) となる
第3節 軌跡と領域
p.108 練習37 直線 \(x+y-3=0\)
p.109 深める 中心 \((4~,~0)\)、半径 \(2\) の円
p.112 練習40\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)

境界線を含まない
\({\small (4)}~\)

境界線を含む
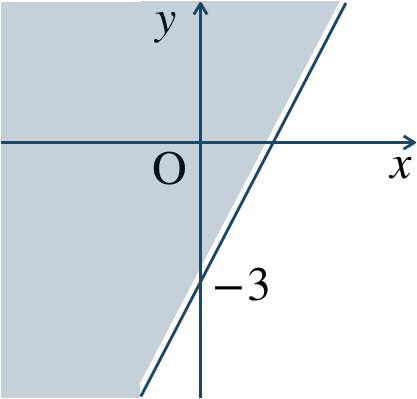
境界線を含まない
\({\small (2)}~\)
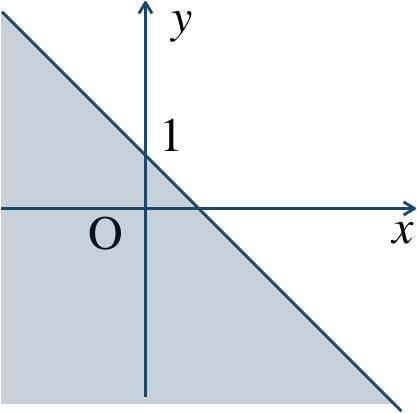
境界線を含む
\({\small (3)}~\)
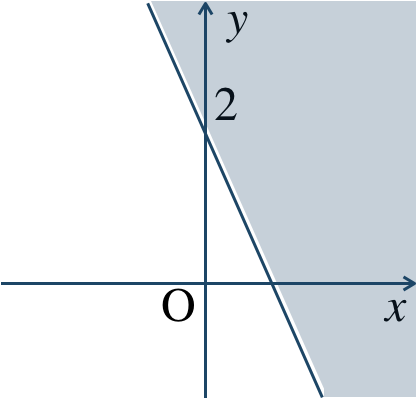
境界線を含まない
\({\small (4)}~\)
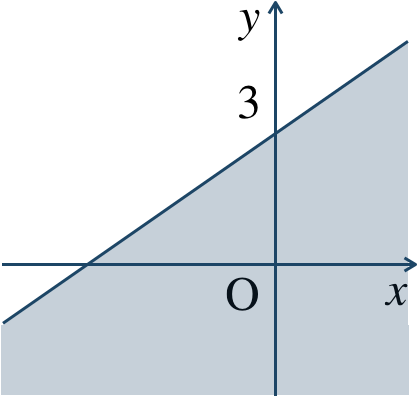
境界線を含む
p.112 問5\({\small (1)}~\)

境界線を含む
\({\small (2)}~\)

境界線を含まない
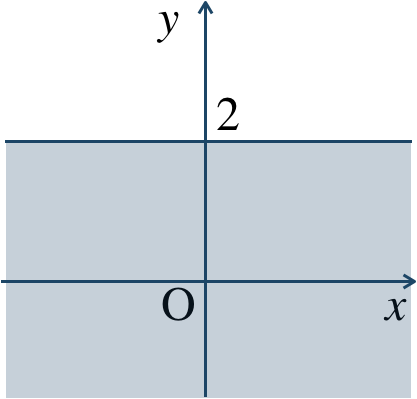
境界線を含む
\({\small (2)}~\)

境界線を含まない
p.112 練習41\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)

境界線を含む

境界線を含まない
\({\small (2)}~\)
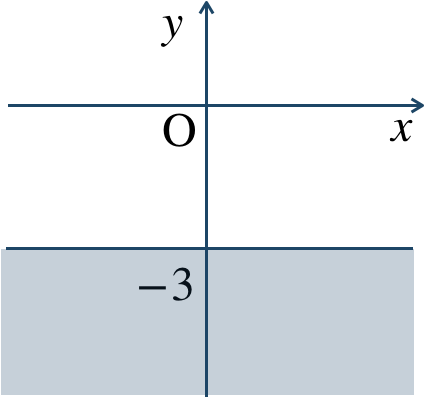
境界線を含む
\({\small (3)}~\)
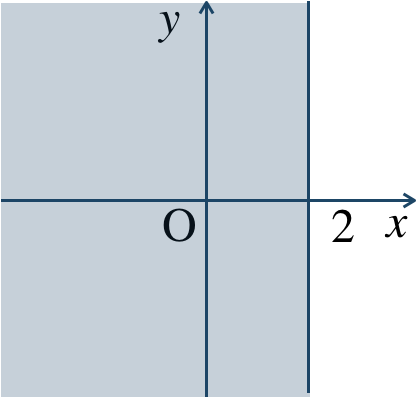
境界線を含む
p.113 問6
境界線を含む
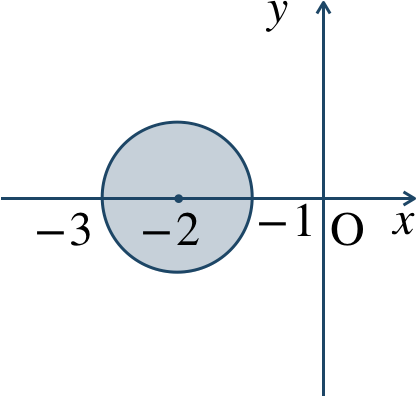
境界線を含む
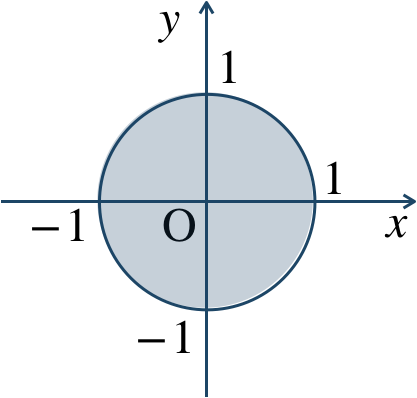
p.113 練習42\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)

境界線を含む
\({\small (4)}~\)

境界線を含まない
境界線を含まない
\({\small (2)}~\)
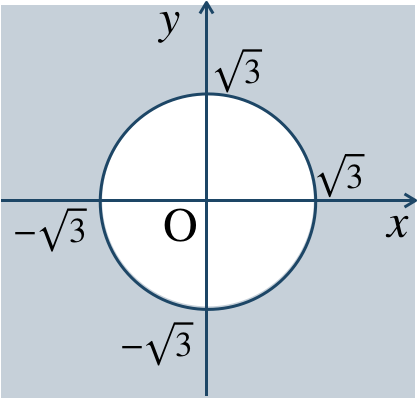
境界線を含む
\({\small (3)}~\)

境界線を含む
\({\small (4)}~\)
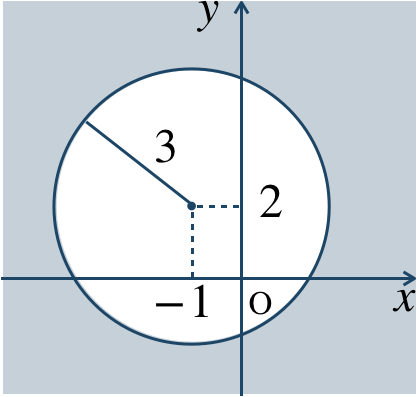
境界線を含まない
p.114 問7$$~~~(x-2)^2+(y+3)^2<25$$
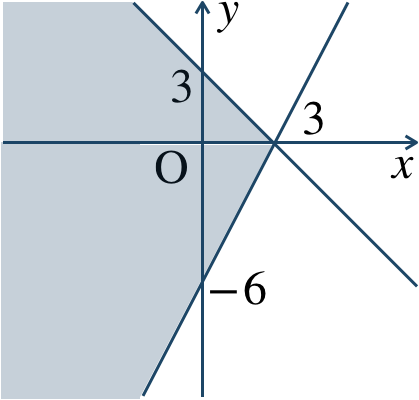
p.114 練習44$${\small (1)}~x-2y+2>0$$$${\small (2)}~(x-2)^2+(y-1)^2<4$$
p.116 深める$$~~~m<\frac{\,3\,}{\,2\,}$$
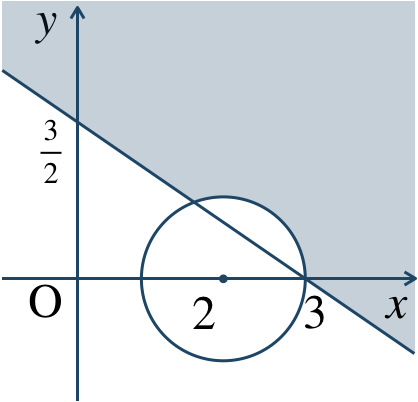
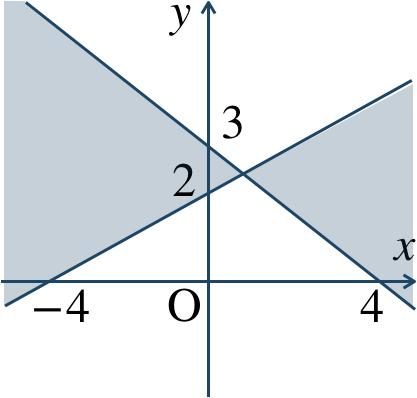
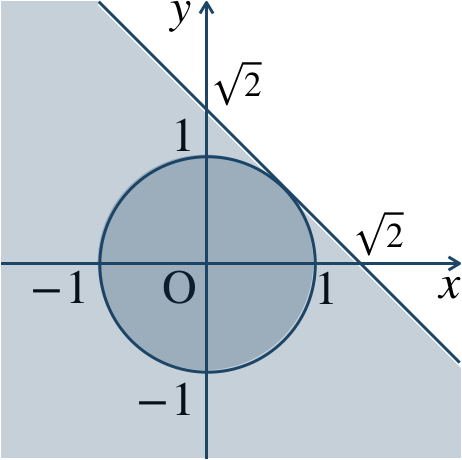
p.117 練習48[証明] \(x^2+y^2<1\) の領域を \(P\)、\(x+y<\sqrt{2}\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2<1\) ならば \(x+y<\sqrt{2}\)
[終]
→ 領域を用いた証明
これらの領域を図示すると次の図のようになる
これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2<1\) ならば \(x+y<\sqrt{2}\)
[終]
→ 領域を用いた証明
p.119 問題20\({\small (1)}~\)

境界線を含まない
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)

境界線を含まない
\({\small (4)}~\)

境界線を含む

境界線を含まない
\({\small (2)}~\)
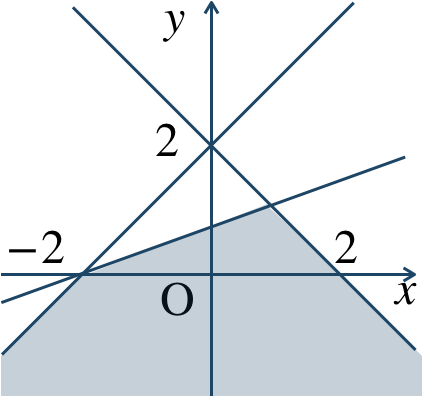
境界線を含む
\({\small (3)}~\)
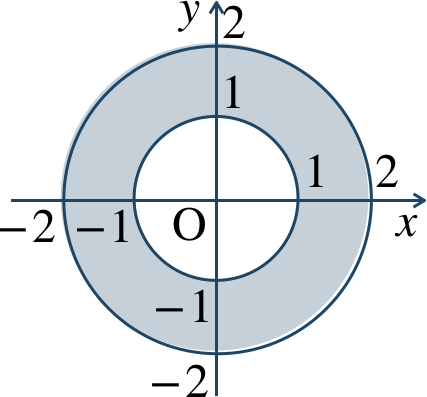
境界線を含まない
\({\small (4)}~\)
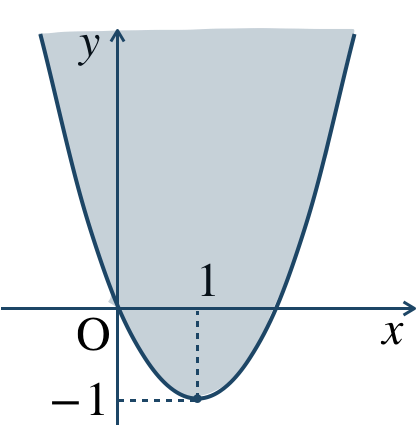
境界線を含む
p.119 問題23[証明] 異なる2点の座標を、\({\rm A}(0~,~0)~,~{\rm B}(a~,~b)\) として、点 \({\rm P}(x~,~y)\) とすると、
\({\rm PA:PB}=m:1\)より、\({\rm PA}^2=m^2{\rm PB}^2\) であるので、$$~~~x^2+y^2=m^2\left\{(x-a)^2+(y-b)^2 \right\}$$計算すると、$$~~~(m^2-1)x^2-2m^2ax+m^2x^2$$$$~~~~~~+(m^2-1)y^2-2m^2by+m^2y^2=0$$これより、
\(m=1\) のとき直線
\(m\neq 1\) のとき円
となる [終]
\({\rm PA:PB}=m:1\)より、\({\rm PA}^2=m^2{\rm PB}^2\) であるので、$$~~~x^2+y^2=m^2\left\{(x-a)^2+(y-b)^2 \right\}$$計算すると、$$~~~(m^2-1)x^2-2m^2ax+m^2x^2$$$$~~~~~~+(m^2-1)y^2-2m^2by+m^2y^2=0$$これより、
\(m=1\) のとき直線
\(m\neq 1\) のとき円
となる [終]
演習問題 図形と方程式
p.120 演習問題A 1[証明]
\(\triangle {\rm ABC}\) の頂点の座標を、
\({\rm A}(x_1~,~y_1)\)\(~,~\)\({\rm B}(x_2~,~y_2)\)\(~,~\)\({\rm C}(x_3~,~y_3)\)
これより、\(\triangle {\rm ABC}\) の重心 \({\rm G}\) は、$$~~~{\rm G}\left(\frac{\,x_1+x_2+x_3\,}{3}~,~\frac{\,y_1+y_2+y_3\,}{3}\right)$$
次に、\({\rm D~,~E~,~F}\) の座標は、$$~~~{\rm D}=\left(\frac{\,nx_2+mx_3\,}{m+n}~,~\frac{\,ny_2+my_3\,}{m+n}\right)$$$$~~~{\rm E}=\left(\frac{\,nx_3+mx_1\,}{m+n}~,~\frac{\,ny_3+my_1\,}{m+n}\right)$$$$~~~{\rm F}=\left(\frac{nx_1+mx_2}{m+n}~,~\frac{\,ny_1+my_2\,}{m+n}\right)$$これより、\(\triangle {\rm DEF}\) の重心 \({\rm G’}=(x~,~y)\) とすると、$$~~~x=\frac{\,1\,}{\,3\,}(\frac{\,nx_2+mx_3\,}{m+n}$$$$~~~~~~~~+\frac{\,nx_3+mx_1\,}{m+n}+\frac{\,nx_1+mx_2\,}{m+n})$$$$~~~~~~=\frac{\,x_1+x_2+x_3\,}{3}$$\(y\) 座標は、$$~~~y=\frac{\,1\,}{\,3\,}(\frac{\,ny_2+my_3\,}{m+n}$$$$~~~~~~~~+\frac{\,ny_3+my_1\,}{m+n}+\frac{\,ny_1+my_2\,}{m+n})$$$$~~~~~~=\frac{\,y_1+y_2+y_3\,}{3}$$したがって、\(\triangle {\rm ABC}\) の重心と \(\triangle {\rm DEF}\) の重心は一致する [終]
\(\triangle {\rm ABC}\) の頂点の座標を、
\({\rm A}(x_1~,~y_1)\)\(~,~\)\({\rm B}(x_2~,~y_2)\)\(~,~\)\({\rm C}(x_3~,~y_3)\)
これより、\(\triangle {\rm ABC}\) の重心 \({\rm G}\) は、$$~~~{\rm G}\left(\frac{\,x_1+x_2+x_3\,}{3}~,~\frac{\,y_1+y_2+y_3\,}{3}\right)$$
次に、\({\rm D~,~E~,~F}\) の座標は、$$~~~{\rm D}=\left(\frac{\,nx_2+mx_3\,}{m+n}~,~\frac{\,ny_2+my_3\,}{m+n}\right)$$$$~~~{\rm E}=\left(\frac{\,nx_3+mx_1\,}{m+n}~,~\frac{\,ny_3+my_1\,}{m+n}\right)$$$$~~~{\rm F}=\left(\frac{nx_1+mx_2}{m+n}~,~\frac{\,ny_1+my_2\,}{m+n}\right)$$これより、\(\triangle {\rm DEF}\) の重心 \({\rm G’}=(x~,~y)\) とすると、$$~~~x=\frac{\,1\,}{\,3\,}(\frac{\,nx_2+mx_3\,}{m+n}$$$$~~~~~~~~+\frac{\,nx_3+mx_1\,}{m+n}+\frac{\,nx_1+mx_2\,}{m+n})$$$$~~~~~~=\frac{\,x_1+x_2+x_3\,}{3}$$\(y\) 座標は、$$~~~y=\frac{\,1\,}{\,3\,}(\frac{\,ny_2+my_3\,}{m+n}$$$$~~~~~~~~+\frac{\,ny_3+my_1\,}{m+n}+\frac{\,ny_1+my_2\,}{m+n})$$$$~~~~~~=\frac{\,y_1+y_2+y_3\,}{3}$$したがって、\(\triangle {\rm ABC}\) の重心と \(\triangle {\rm DEF}\) の重心は一致する [終]
p.120 演習問題A 4\({\small (1)}~{\large \frac{\,|x_1y_2-x_2y_1|\,}{\,\sqrt{x_1^2+y_1^2}\,}}\)
\({\small (2)}~\)[証明]
\(\triangle {\rm OAB}\) の底辺を \({\rm OA}\) とすると、
\({\rm OA}=\sqrt{x_1^2+y_1^2}\)
また、高さは点 \({\rm B}\) と直線 \({\rm OA}\) との距離となる
(1) の解を用いると、
\(\triangle {\rm OAB}\)
\(={\large \frac{\,1\,}{\,2\,}}\cdot{\rm OA}\cdot d\)
\(={\large \frac{\,1\,}{\,2\,}}\cdot\sqrt{x_1^2+y_1^2}\cdot{\large \frac{\,|x_1y_2-x_2y_1|\,}{\sqrt{x_1^2+y_1^2}}}\)
\(={\large \frac{\,1\,}{\,2\,}}|x_1y_2-x_2y_1|\)
[終]
\({\small (2)}~\)[証明]
\(\triangle {\rm OAB}\) の底辺を \({\rm OA}\) とすると、
\({\rm OA}=\sqrt{x_1^2+y_1^2}\)
また、高さは点 \({\rm B}\) と直線 \({\rm OA}\) との距離となる
(1) の解を用いると、
\(\triangle {\rm OAB}\)
\(={\large \frac{\,1\,}{\,2\,}}\cdot{\rm OA}\cdot d\)
\(={\large \frac{\,1\,}{\,2\,}}\cdot\sqrt{x_1^2+y_1^2}\cdot{\large \frac{\,|x_1y_2-x_2y_1|\,}{\sqrt{x_1^2+y_1^2}}}\)
\(={\large \frac{\,1\,}{\,2\,}}|x_1y_2-x_2y_1|\)
[終]
p.121 演習問題B 9[証明] \(x+2y=1\) と \(3x-4y=1\) の交点は、連立することより、
\(\left({\large \frac{\,3\,}{\,5\,}}~,~{\large \frac{\,1\,}{\,5\,}}\right)\)
これは、\(ax+by=1\) 上にもあるので、
\(3a+b-5=0\) …①
次に、2点 \((1~,~2)~,~(3~,~-4)\) を通る直線の方程式は、
\(y-2={\large \frac{\,-4-2\,}{\,3-1\,}}(x-1)\)
これより、
\(3x+y-5=0\) …②
①より②に点 \((a~,~b)\) を代入した式が成り立ち、点 \((a~,~b)\) は②上にある
したがって、3点 \((1~,~2)\)\(~,~\)\((3~,~-4)\)\(~,~\)\((a~,~b)\) は一直線上にある [終]
\(\left({\large \frac{\,3\,}{\,5\,}}~,~{\large \frac{\,1\,}{\,5\,}}\right)\)
これは、\(ax+by=1\) 上にもあるので、
\(3a+b-5=0\) …①
次に、2点 \((1~,~2)~,~(3~,~-4)\) を通る直線の方程式は、
\(y-2={\large \frac{\,-4-2\,}{\,3-1\,}}(x-1)\)
これより、
\(3x+y-5=0\) …②
①より②に点 \((a~,~b)\) を代入した式が成り立ち、点 \((a~,~b)\) は②上にある
したがって、3点 \((1~,~2)\)\(~,~\)\((3~,~-4)\)\(~,~\)\((a~,~b)\) は一直線上にある [終]
次のページ「第4章 三角関数」