文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第4章 三角関数
第5章 指数関数と対数関数
第6章 微分法と積分法
第3章 図形と方程式
第1節 点と直線
p.68 練習1$${\small (1)}~7$$$${\small (2)}~2$$$${\small (3)}~3$$
p.69 練習2\({\small (1)}~1:2\) に内分
\({\small (2)}~3:2\) に外分
\({\small (3)}~1:3\) に外分
\({\small (2)}~3:2\) に外分
\({\small (3)}~1:3\) に外分
p.70 練習3$${\small (1)}~{\rm C}\left({ \frac{\,32\,}{\,5\,}}\right)$$$${\small (2)}~{\rm D}(10)$$$${\small (3)}~{\rm E}(-4)$$$${\small (4)}~{\rm M}(6)$$→ 直線上の線分の長さ・内分点・外分点
p.71 練習4$${\small (1)}~5$$$${\small (2)}~5\sqrt{2}$$$${\small (3)}~2$$$${\small (4)}~\sqrt{13}$$
p.72 練習5$$~~~(0,3)$$→ 平面上の線分の長さ
p.72 練習6[証明] 座標平面上に4点 \({\rm A~,~B~,~C~,~D}\) を次のようにとると、
\({\rm A}(a,b)\) \({\rm B}(-c,0)\)
\({\rm C}(2c,0)\) \({\rm D}(0,0)\)
このとき、
\({\rm AB}^2=(-c-a)^2+(-b)^2\)
\(=a^2+b^2+c^2+2ca\)
\({\rm AC}^2=(2c-a)^2+(-b)^2\)
\(=a^2+b^2+4c^2-4ca\)
よって、
\(2{\rm AB}^2+{\rm AC}^2\)
\(=3(a^2+b^2+2c^2)\)
また、
\({\rm AD}^2=a^2+b^2\)
\({\rm BD}^2=(-c)^2=c^2\)
よって、
\({\rm AD}^2+2{\rm BD}^2\)
\(=a^2+b^2+2c^2\)
したがって、
\(2{\rm AB}^2+{\rm AC}^2=3({\rm AD}^2+2{\rm BD}^2)\) [終]
→ 座標を利用した等式の証明
\({\rm A}(a,b)\) \({\rm B}(-c,0)\)
\({\rm C}(2c,0)\) \({\rm D}(0,0)\)
このとき、
\({\rm AB}^2=(-c-a)^2+(-b)^2\)
\(=a^2+b^2+c^2+2ca\)
\({\rm AC}^2=(2c-a)^2+(-b)^2\)
\(=a^2+b^2+4c^2-4ca\)
よって、
\(2{\rm AB}^2+{\rm AC}^2\)
\(=3(a^2+b^2+2c^2)\)
また、
\({\rm AD}^2=a^2+b^2\)
\({\rm BD}^2=(-c)^2=c^2\)
よって、
\({\rm AD}^2+2{\rm BD}^2\)
\(=a^2+b^2+2c^2\)
したがって、
\(2{\rm AB}^2+{\rm AC}^2=3({\rm AD}^2+2{\rm BD}^2)\) [終]
→ 座標を利用した等式の証明
p.72 深める点 \({\rm A}\) が \(y\) 軸上に定まるので不適
p.74 練習7$${\small (1)}~{\rm C}\left({\large \frac{5}{3}},4\right)$$$${\small (2)}~{\rm D}(11,8)$$$${\small (3)}~{\rm E}(-17,-4)$$$${\small (4)}~{\rm M}\left({ \frac{\,1\,}{\,2\,}},{ \frac{\,7\,}{\,2\,}}\right)$$→ 平面上の内分点・外分点・重心
p.74 練習8$$~~~(-6,8)$$→ 点に対して対称な点
p.75 練習9$$~~~\left({ \frac{\,x_1+x_2+x_3\,}{3}},{ \frac{\,y_1+y_2+y_3\,}{3}}\right)$$
p.75 練習10$${\small (1)}~\left(3,{ \frac{\,7\,}{\,3\,}}\right)$$$${\small (2)}~\left(0,{ \frac{\,2\,}{\,3\,}}\right)$$→ 平面上の内分点・外分点・重心
p.76 練習11$${\small (1)}~y=3x+1$$$${\small (2)}~y=-1$$$${\small (3)}~x=2$$
p.77 練習12$${\small (1)}~y=3x-10$$$${\small (2)}~y=-2x-5$$→ 直線の方程式
p.78 練習13$${\small (1)}~y=2x-4$$$${\small (2)}~y=-2x+2$$$${\small (3)}~y=-1$$$${\small (4)}~x=3$$→ 2点を通る直線の方程式
p.78 練習14[証明] 2点 \((a,0)~,~(0,b)\) を通る直線であるので、
\(y-0={\large \frac{\,b-0\,}{\,0-a\,}}(x-a)\)
これより、
\(y=-{\large \frac{\,b\,}{\,a\,}}x+b\)
移項すると、
\({\large \frac{\,bx\,}{\,a\,}}+y=b\)
両辺を \(b\) で割ると、
\({\large \frac{\,x\,}{\,a\,}}+{\large \frac{\,y\,}{\,b\,}}=1\) [終]
\(y-0={\large \frac{\,b-0\,}{\,0-a\,}}(x-a)\)
これより、
\(y=-{\large \frac{\,b\,}{\,a\,}}x+b\)
移項すると、
\({\large \frac{\,bx\,}{\,a\,}}+y=b\)
両辺を \(b\) で割ると、
\({\large \frac{\,x\,}{\,a\,}}+{\large \frac{\,y\,}{\,b\,}}=1\) [終]
p.79 練習15 ②、③
p.80 練習16\({\small (1)}~\)平行
\({\small (2)}~\)垂直
\({\small (3)}~\)平行
\({\small (4)}~\)垂直
\({\small (2)}~\)垂直
\({\small (3)}~\)平行
\({\small (4)}~\)垂直
p.81 練習18$$~~~(-2,3)$$→ 直線に対して対称な点
p.82 練習19$${\small (1)}~\sqrt{5}$$$${\small (2)}~{ \frac{\,4\sqrt{13}\,}{\,13\,}}$$
p.83 練習20$${\small (1)}~{ \frac{\,6\,}{\,5\,}}$$$${\small (2)}~{ \frac{\,2\sqrt{5}\,}{\,5\,}}$$$${\small (3)}~\sqrt{10}$$→ 点と直線との距離
p.84 研究 練習1$$~~~2x-3y+7=0$$→ 2直線の交点を通る直線
p.84 深める③は、\(x+2y-4=0\) を表すことができない
④は、\(x-y-1=0\) を表すことができない
④は、\(x-y-1=0\) を表すことができない
p.85 問題 1[証明]
2点間の距離の公式より、
\({\rm OA}^2=6^2+2^2=40\)
\({\rm OB}^2=2^2+4^2=20\)
\({\rm AB}^2=(2-6)^2+(4-2)^2=20\)
これらより、
\({\rm OA}^2={\rm OB}^2+{\rm AB}^2\)
三平方の定理の逆より、
\(\angle{\rm ABO}=90^\circ\)
また、\({\rm OB=AB}\) となる
したがって、
\(\triangle {\rm OAB}\) は \(\angle{\rm ABO}=90^\circ\) で \({\rm OB=AB}\) の直角二等辺三角形である [終]
2点間の距離の公式より、
\({\rm OA}^2=6^2+2^2=40\)
\({\rm OB}^2=2^2+4^2=20\)
\({\rm AB}^2=(2-6)^2+(4-2)^2=20\)
これらより、
\({\rm OA}^2={\rm OB}^2+{\rm AB}^2\)
三平方の定理の逆より、
\(\angle{\rm ABO}=90^\circ\)
また、\({\rm OB=AB}\) となる
したがって、
\(\triangle {\rm OAB}\) は \(\angle{\rm ABO}=90^\circ\) で \({\rm OB=AB}\) の直角二等辺三角形である [終]
p.85 問題 6[証明]
それぞれの直線の傾きは、
\(-{\large \frac{\,a\,}{\,b\,}}~,~-{\large \frac{\,a’\,}{\,b’\,}}\)
これより、2直線が平行となるので、
\(-{\large \frac{\,a\,}{\,b\,}}=-{\large \frac{\,a’\,}{\,b’\,}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
また、2直線が垂直となるので、
\(\left(-{\large \frac{\,a\,}{\,b\,}}\right)\left(-{\large \frac{\,a’\,}{\,b’\,}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
[終]
それぞれの直線の傾きは、
\(-{\large \frac{\,a\,}{\,b\,}}~,~-{\large \frac{\,a’\,}{\,b’\,}}\)
これより、2直線が平行となるので、
\(-{\large \frac{\,a\,}{\,b\,}}=-{\large \frac{\,a’\,}{\,b’\,}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
また、2直線が垂直となるので、
\(\left(-{\large \frac{\,a\,}{\,b\,}}\right)\left(-{\large \frac{\,a’\,}{\,b’\,}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
[終]
p.85 問題 7直線 \({\rm AB}\) の傾きは、\(a\neq b\) より
\({\large \frac{\,a-b\,}{\,b-a\,}}=-1\)
また、直線 \(y=x\) の傾きは \(1\)
よって、2直線の傾きの積が \(-1\) となり、2直線は垂直に交わる
また、線分 \({\rm AB}\) の中点は、
\(\left({\large \frac{\,a+b\,}{\,2\,}},{\large \frac{\,b+a\,}{\,2\,}}\right)\)
これを \(y=x\) に代入すると、
\({\large \frac{\,b+a\,}{2}}={\large \frac{\,a+b\,}{2}}\)
これより、線分 \({\rm AB}\) の中点は直線 \(y=x\) 上にある
したがって、
2点 \({\rm A~,~B}\) は直線 \(y=x\) に関して対称である [終]
\({\large \frac{\,a-b\,}{\,b-a\,}}=-1\)
また、直線 \(y=x\) の傾きは \(1\)
よって、2直線の傾きの積が \(-1\) となり、2直線は垂直に交わる
また、線分 \({\rm AB}\) の中点は、
\(\left({\large \frac{\,a+b\,}{\,2\,}},{\large \frac{\,b+a\,}{\,2\,}}\right)\)
これを \(y=x\) に代入すると、
\({\large \frac{\,b+a\,}{2}}={\large \frac{\,a+b\,}{2}}\)
これより、線分 \({\rm AB}\) の中点は直線 \(y=x\) 上にある
したがって、
2点 \({\rm A~,~B}\) は直線 \(y=x\) に関して対称である [終]
第2節 円
p.86 練習21$${\small (1)}~x^2+y^2=4$$$${\small (2)}~(x-2)^2+(y-3)^2=16$$$${\small (3)}~(x+2)^2+(y-1)^2=10$$→ 円の方程式
p.86 練習22 中心 \((3,-2)\)、半径 \(2\sqrt{2}\)
p.87 練習23 中心 \((-1,4)\)、半径 \(2\sqrt{2}\)
\((x+1)^2+(y-4)^2=8\)
\((x+1)^2+(y-4)^2=8\)
p.88 練習25$${\small (1)}~x^2+y^2-3x+5y-4=0$$$${\small (2)}~x^2+y^2-2x+4y-20=0$$→ 円の方程式の決定①(点の条件)
p.89 練習26$${\small (1)}~(3,4)~,~(-4,-3)$$$${\small (2)}~(2,2)$$→ 円と直線との共有点
p.90 練習27$${\small (1)}~-5≦m≦5$$\({\small (2)}~\)
\(m=5\) のとき \((-2,1)\)
\(m=-5\) のとき \((2,-1)\)
→ 円と直線との位置関係
\(m=5\) のとき \((-2,1)\)
\(m=-5\) のとき \((2,-1)\)
→ 円と直線との位置関係
p.91 練習28$$~~~\sqrt{5}$$→ 円と直線との位置関係
p.91 深める$$~~~(3,1)$$
p.93 練習29$${\small (1)}~3x+y-10=0$$$${\small (2)}~2x-3y-13=0$$$${\small (3)}~x=4$$$${\small (4)}~y=-\sqrt{5}$$
p.93 練習30$$~~~y=1~,~(0,1)$$$$~~~4x-3y-5=0~,~\left({ \frac{\,4\,}{\,5\,}},-{ \frac{\,3\,}{\,5\,}}\right)$$→ 円の接線の方程式
p.95 練習31\({\small (1)}~\)外接する
\({\small (2)}~\)2点で交わる
\({\small (2)}~\)2点で交わる
p.95 練習32$$~~~(x+3)^2+(y-4)^2=36$$→ 2つの円の位置関係
p.96 練習33$$~~~(1,3)~,~(3,-1)$$→ 2つの円の共有点の座標
p.97 研究 練習1$$~~~x^2+y^2-2x+y-5=0$$→ 2つの円の交点を通る円・直線
第3節 軌跡と領域
p.99 練習34 直線 \(x=2\)
p.103 練習37\({\small (1)}~\)





境界線を含む
\({\small (2)}~\)

境界線を含む
\({\small (3)}~\)
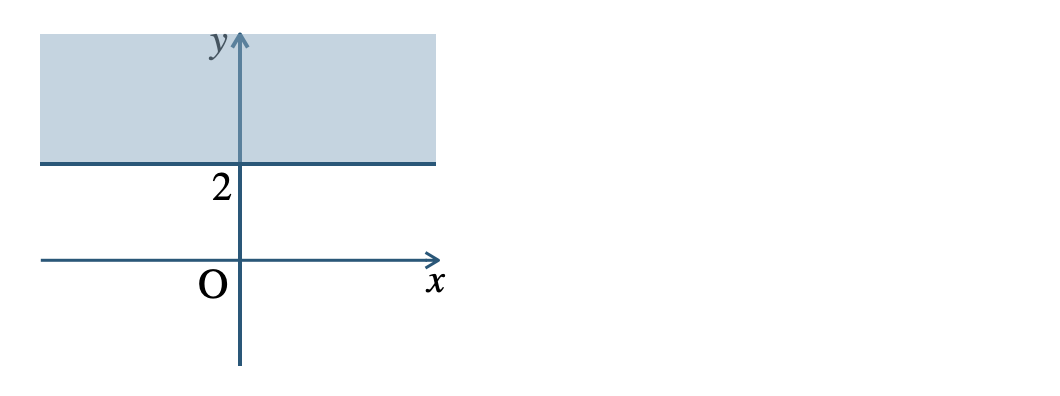
境界線を含まない
\({\small (4)}~\)
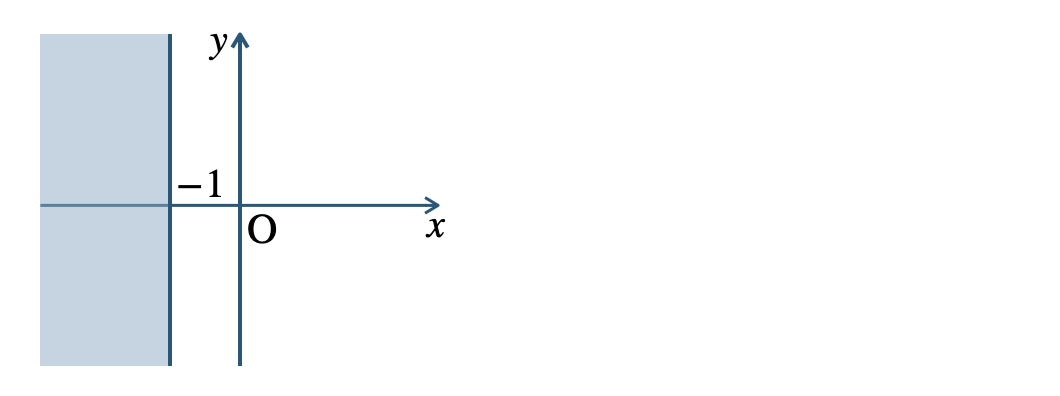
境界線を含む
p.104 練習38\({\small (1)}~\)





境界線を含まない
\({\small (2)}~\)
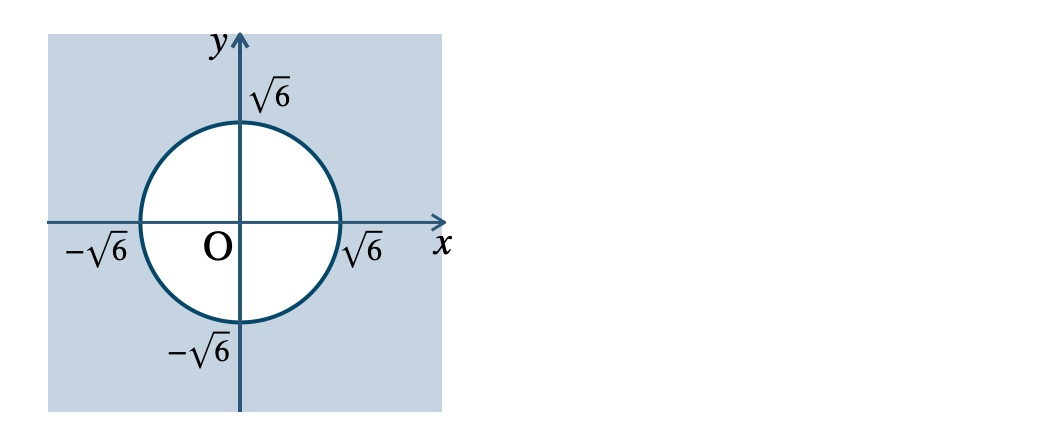
境界線を含む
\({\small (3)}~\)
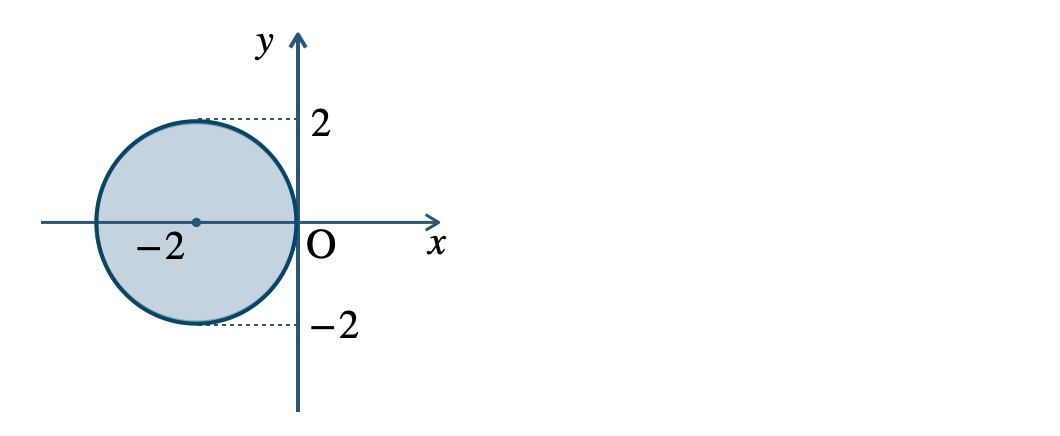
境界線を含む
\({\small (4)}~\)
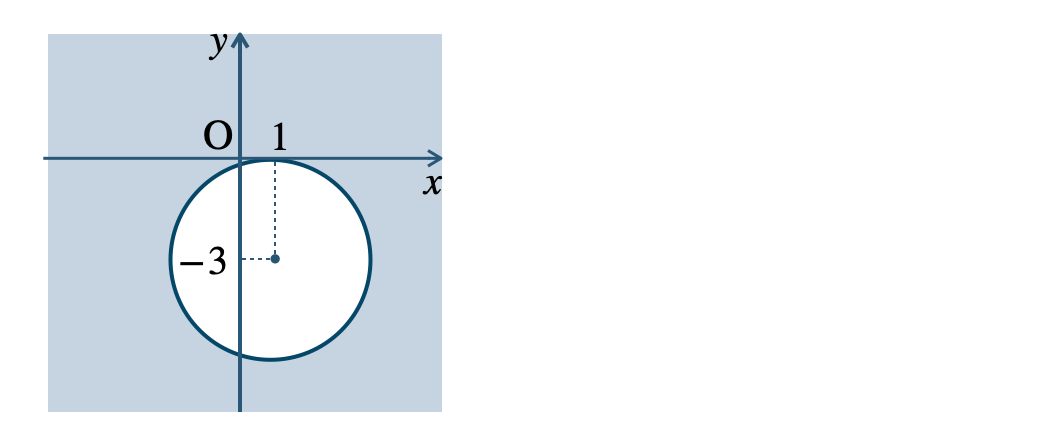
境界線を含まない
→ 不等式の表す領域
p.106 練習39\({\small (1)}~\)




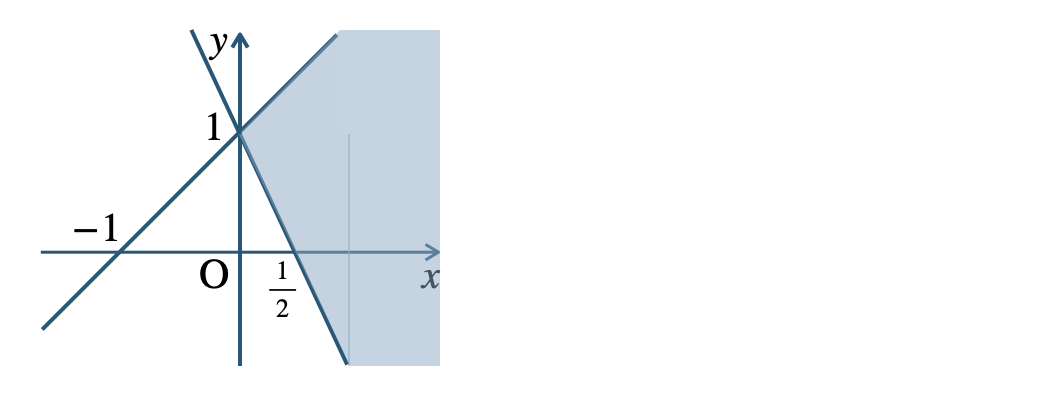
境界線を含まない
\({\small (2)}~\)
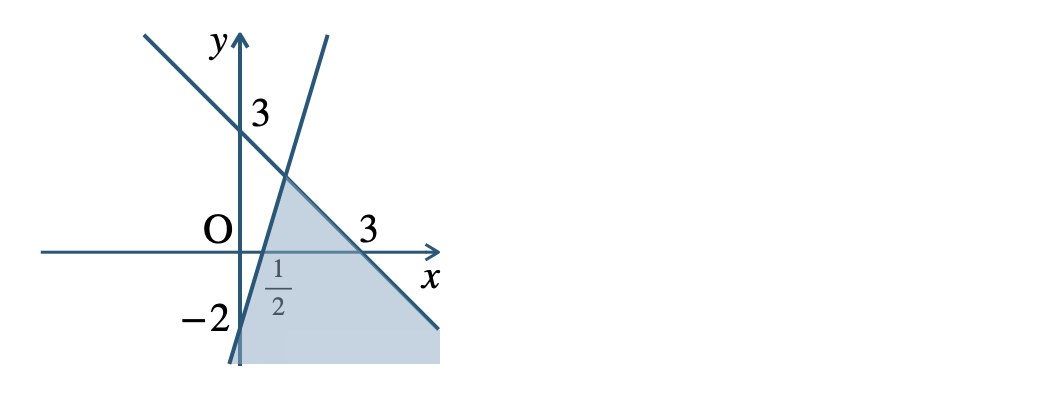
境界線を含む
\({\small (3)}~\)

境界線を含まない
\({\small (4)}~\)
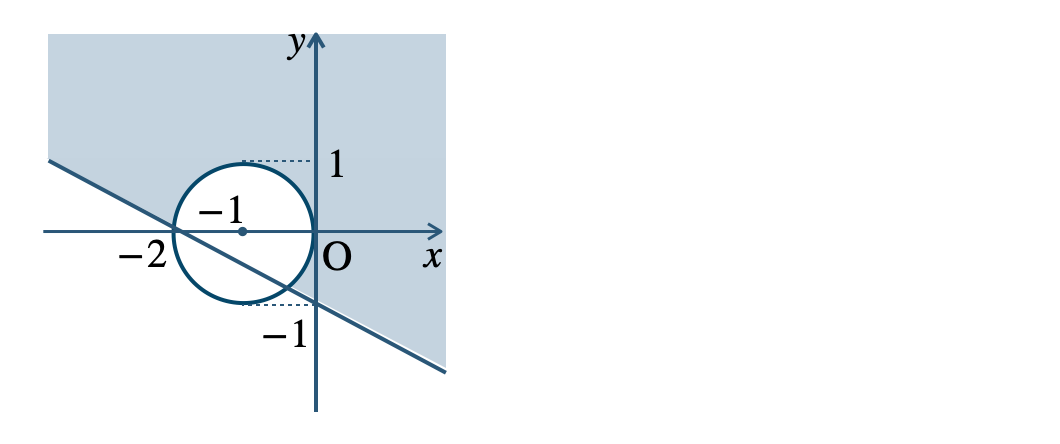
境界線を含む
→ 連立不等式の表す領域①
p.107 深める \(x=4~,~y=0\) で最大値 \(12\)
p.108 練習42[証明] \(x^2+y^2≦1\) の領域を \(P\)、\(x+y≦\sqrt{2}\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2≦1\) ならば \(x+y≦\sqrt{2}\)
[終]
→ 領域を用いた証明
これらの領域を図示すると次の図のようになる
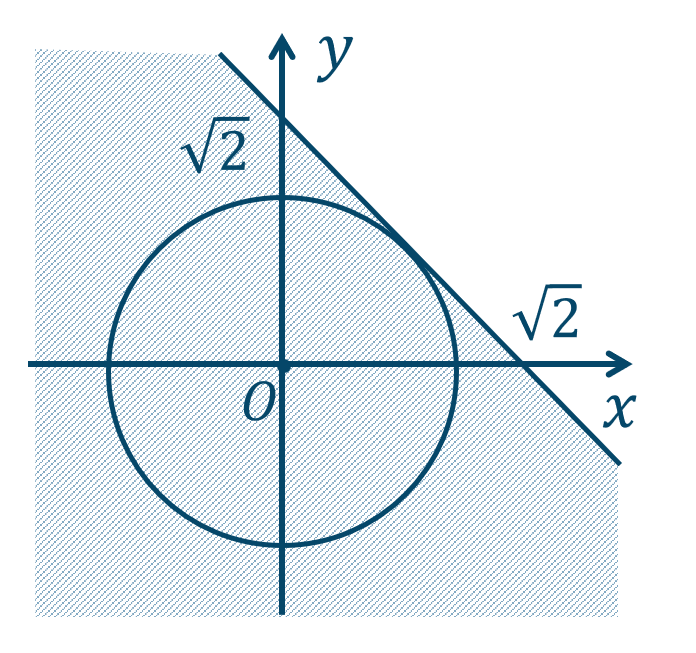
これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2≦1\) ならば \(x+y≦\sqrt{2}\)
[終]
→ 領域を用いた証明
p.109 研究 練習1\({\small (1)}~\)


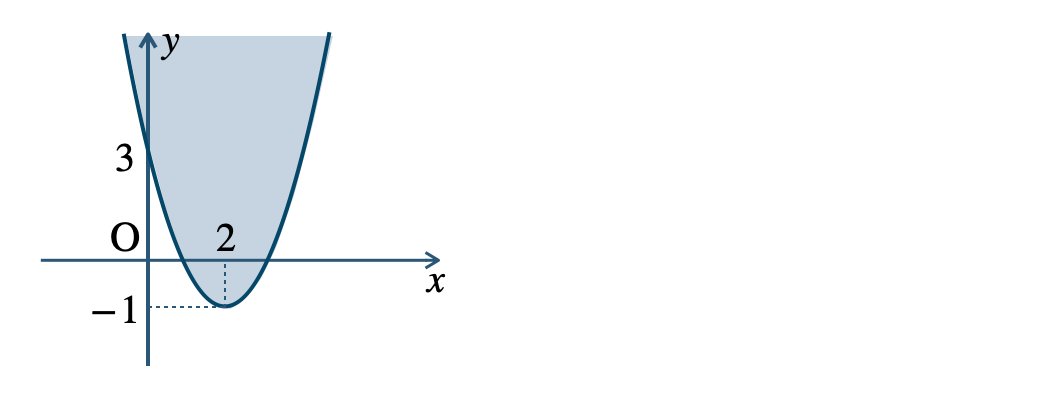
境界線を含まない
\({\small (2)}~\)
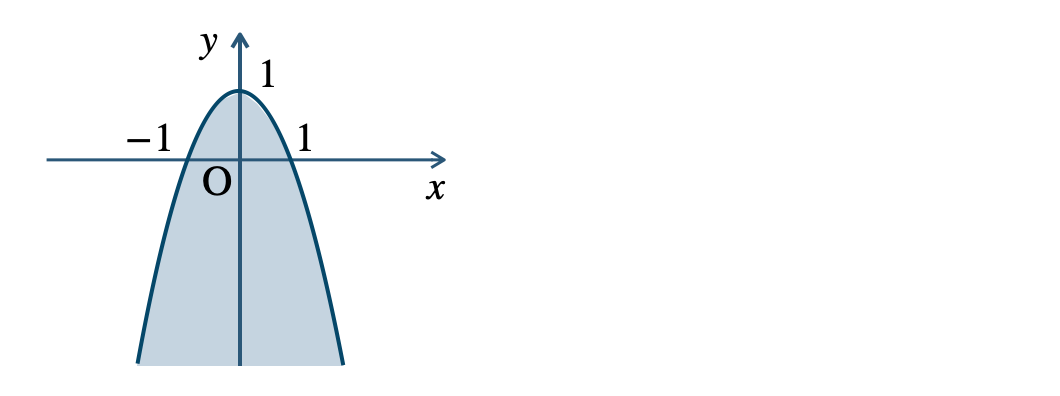
境界線を含む
p.110 問題18\({\small (1)}~\)


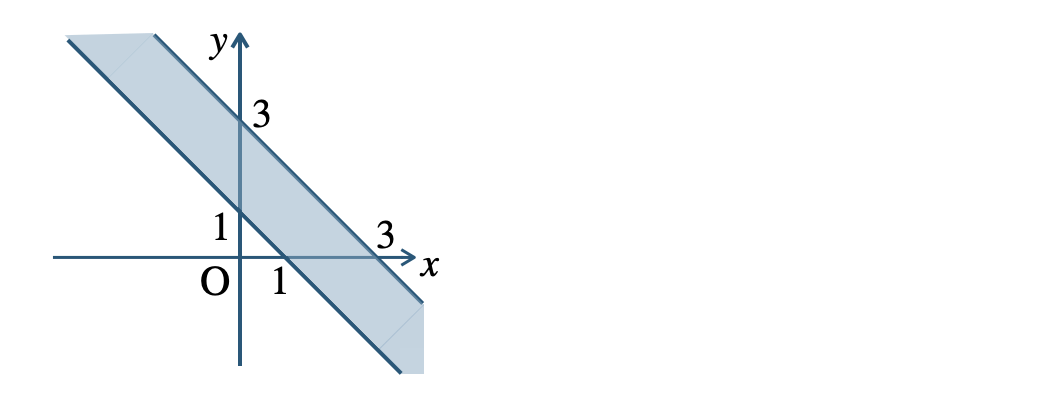
境界線を含む
\({\small (2)}~\)
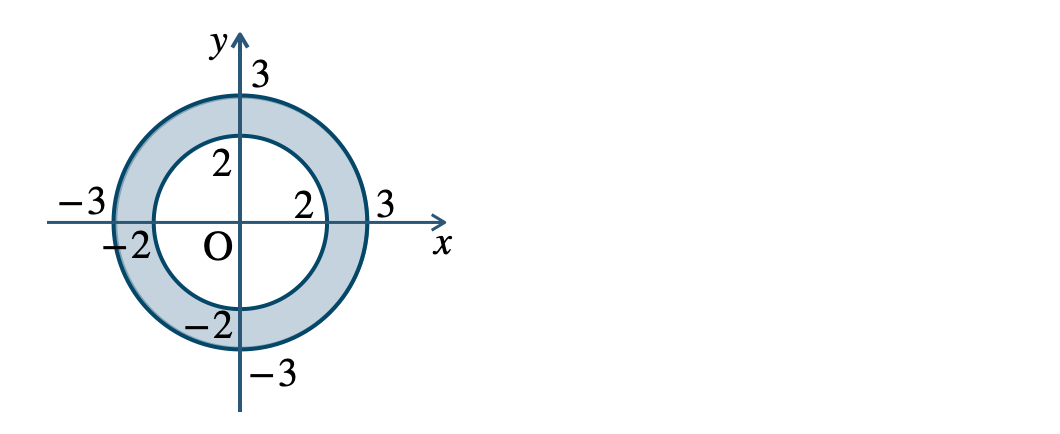
境界線を含む
p.110 問題19

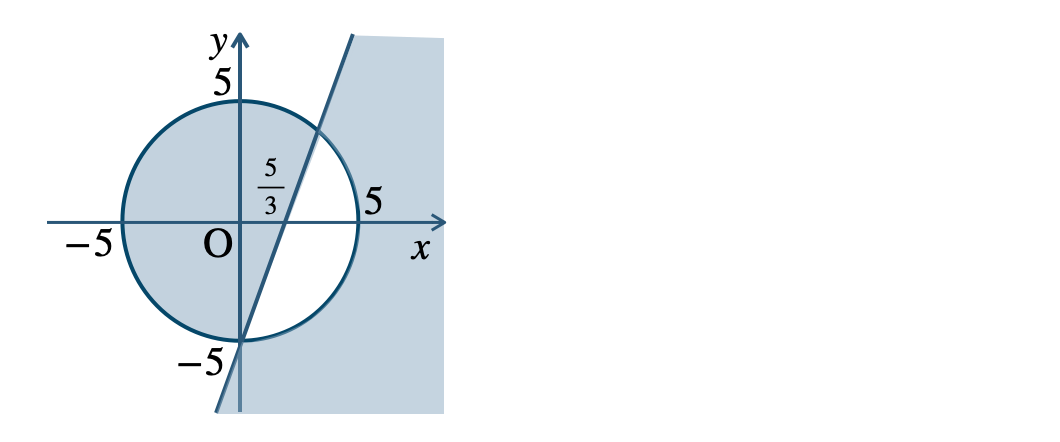
境界線を含む
章末問題 図形と方程式
章末問題A
p.111 章末問題A 4$${\small (1)}~{ \frac{\,|x_1y_2-x_2y_1|\,}{\,\sqrt{x_1^2+y_1^2}\,}}$$\({\small (2)}~\)
[証明]
\(\triangle {\rm OAB}\) の底辺を \({\rm OA}\) とすると、
\({\rm OA}=\sqrt{x_1^2+y_1^2}\)
また、高さは点 \({\rm B}\) と直線 \({\rm OA}\) との距離となる
(1) の解を用いると、
\(\triangle {\rm OAB}\)
\(={\large \frac{1}{\,2\,}}\cdot{\rm OA}\cdot d\)
\(={\large \frac{1}{\,2\,}}\cdot\sqrt{x_1^2+y_1^2}\cdot{\large \frac{\,|x_1y_2-x_2y_1|\,}{\,\sqrt{x_1^2+y_1^2}\,}}\)
\(={\large \frac{1}{\,2\,}}|x_1y_2-x_2y_1|\)
[終]
[証明]
\(\triangle {\rm OAB}\) の底辺を \({\rm OA}\) とすると、
\({\rm OA}=\sqrt{x_1^2+y_1^2}\)
また、高さは点 \({\rm B}\) と直線 \({\rm OA}\) との距離となる
(1) の解を用いると、
\(\triangle {\rm OAB}\)
\(={\large \frac{1}{\,2\,}}\cdot{\rm OA}\cdot d\)
\(={\large \frac{1}{\,2\,}}\cdot\sqrt{x_1^2+y_1^2}\cdot{\large \frac{\,|x_1y_2-x_2y_1|\,}{\,\sqrt{x_1^2+y_1^2}\,}}\)
\(={\large \frac{1}{\,2\,}}|x_1y_2-x_2y_1|\)
[終]
次のページ「第4章 三角関数」