文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第4章 三角関数
第5章 指数関数と対数関数
第6章 微分法と積分法
第4章 三角関数
第1節 三角関数
p.115 練習1\({\small (1)}~\)






\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

\({\small (5)}~\)

p.115 練習2$$~~~420^\circ~,~-300^\circ$$→ 動径と一般角
p.116 練習3\({\small (1)}~\)
[証明]
弧の長さ \(1\) に対する中心角の大きさが \(1\) ラジアンである
中心角 \(180^\circ\) の弧は半円となるので、弧の長さは、
\(2\pi \times {\large \frac{\,1\,}{\,2\,}}=\pi\)
したがって、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンである
[終]
\({\small (2)}~\)
[証明]
\(1\) ラジアンに対する中心角の大きさを \(a^\circ\) とする
(1) の結果より、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンであるので、
\(\pi:180^\circ=1:a^\circ\)
よって、
\(a={\large \frac{\,180\,}{\,\pi\,}}\)
したがって、
\(1\) ラジアンは \(\left({\large \frac{\,180\,}{\,\pi\,}}\right)^\circ\)
[終]
[証明]
弧の長さ \(1\) に対する中心角の大きさが \(1\) ラジアンである
中心角 \(180^\circ\) の弧は半円となるので、弧の長さは、
\(2\pi \times {\large \frac{\,1\,}{\,2\,}}=\pi\)
したがって、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンである
[終]
\({\small (2)}~\)
[証明]
\(1\) ラジアンに対する中心角の大きさを \(a^\circ\) とする
(1) の結果より、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンであるので、
\(\pi:180^\circ=1:a^\circ\)
よって、
\(a={\large \frac{\,180\,}{\,\pi\,}}\)
したがって、
\(1\) ラジアンは \(\left({\large \frac{\,180\,}{\,\pi\,}}\right)^\circ\)
[終]
p.116 練習4$${\small (1)}~{ \frac{\,7\,}{\,6\,}}\pi$$$${\small (2)}~{ \frac{\,4\,}{\,3\,}}\pi$$$${\small (3)}~{ \frac{\,11\,}{\,6\,}}\pi$$$${\small (4)}~225^\circ$$$${\small (5)}~270^\circ$$→ 弧度法と扇形
p.117 練習5$${\small (1)}~l={ \frac{\,4\,}{\,3\,}}\pi~,~S={ \frac{\,8\,}{\,3\,}}\pi$$$${\small (2)}~l=7\pi~,~S=21\pi$$→ 弧度法と扇形
p.119 練習6$${\small (1)}~\sin{{ \frac{\,5\,}{4}}\pi}=-{ \frac{1}{\,\sqrt{2}\,}}~,~\cos{{ \frac{\,5\,}{4}}\pi}=-{ \frac{1}{\,\sqrt{2}\,}}$$$$~~~\tan{{ \frac{\,5\,}{4}}\pi}=1$$$${\small (2)}~\sin{{ \frac{\,11\,}{6}}\pi}=-{ \frac{1}{\,2\,}}~,~\cos{{ \frac{\,11\,}{6}}\pi}={ \frac{\,\sqrt{3}\,}{2}}$$$$~~~\tan{{ \frac{\,11\,}{6}}\pi}=-{ \frac{1}{\,\sqrt{3}\,}}$$$${\small (3)}~\sin{\left(-{ \frac{\,\pi\,}{3}}\right)}=-{ \frac{\,\sqrt{3}\,}{2}}$$$$~~~\cos{\left(-{ \frac{\,\pi\,}{3}}\right)}={ \frac{1}{\,2\,}}$$$$~~~\tan{\left(-{ \frac{\,\pi\,}{3}}\right)}=-\sqrt{3}$$→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
p.119 練習7\({\small (1)}~\)第4象限
\({\small (2)}~\)第3象限
\({\small (2)}~\)第3象限
p.120 練習8$$~~~\cos{\theta}={ \frac{\,2\sqrt{2}\,}{3}}~,~\tan{\theta}=-{ \frac{1}{\,2\sqrt{2}\,}}$$
p.120 練習9$$~~~\cos{\theta}=-{ \frac{1}{\,\sqrt{5}\,}}~,~\sin{\theta}=-{ \frac{2}{\,\sqrt{5}\,}}$$→ 三角関数の相互関係の公式
p.120 深める\(1+\tan^2{\theta}={\large \frac{\,1\,}{\,\cos^2{\theta}\,}}\) より、$$\begin{eqnarray}~~~1+\tan^2{\theta}&=&\frac{\,25\,}{\,9\,}\\[2pt]~~~\tan^2{\theta}&=&\frac{\,16\,}{\,9\,}\end{eqnarray}$$\(\tan{m}>0\) より、$$~~~\tan{\theta}=\frac{\,4\,}{\,3\,}$$また、\(\sin{\theta}=\tan{\theta}\cos{\theta}\) より、$$~~~\sin{\theta}=\frac{\,4\,}{\,3\,}\times\left(~\frac{\,3\,}{\,5\,}\right)=-\frac{\,4\,}{\,5\,}$$
p.121 練習10$${\small (1)}~{ \frac{4}{\,9\,}}$$$${\small (2)}~{ \frac{13}{\,27\,}}$$→ 三角関数の式の値
p.121 練習11[証明]
(左辺)$$\begin{eqnarray}~&=&\tan^2{\theta}-\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}\,}{\cos^2{\theta}}-\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}-\sin^2{\theta}\cos^2{\theta}\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^2{\theta}(1-\cos^2{\theta})\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^2{\theta}\cdot\sin^2{\theta}\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^4{\theta}\,}{\cos^2{\theta}}\end{eqnarray}$$ (右辺)$$\begin{eqnarray}~&=&\tan^2{\theta}\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}\,}{\cos^2{\theta}}\cdot\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^4{\theta}\,}{\cos^2{\theta}}\end{eqnarray}$$したがって、$$~~~\tan^2{\theta}-\sin^2{\theta}=\tan^2{\theta}\sin^2{\theta}$$[終]
→ 三角関数の等式の証明
(左辺)$$\begin{eqnarray}~&=&\tan^2{\theta}-\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}\,}{\cos^2{\theta}}-\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}-\sin^2{\theta}\cos^2{\theta}\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^2{\theta}(1-\cos^2{\theta})\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^2{\theta}\cdot\sin^2{\theta}\,}{\cos^2{\theta}}\\[2pt]~&=&\frac{\,\sin^4{\theta}\,}{\cos^2{\theta}}\end{eqnarray}$$ (右辺)$$\begin{eqnarray}~&=&\tan^2{\theta}\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^2{\theta}\,}{\cos^2{\theta}}\cdot\sin^2{\theta}\\[2pt]~&=&\frac{\,\sin^4{\theta}\,}{\cos^2{\theta}}\end{eqnarray}$$したがって、$$~~~\tan^2{\theta}-\sin^2{\theta}=\tan^2{\theta}\sin^2{\theta}$$[終]
→ 三角関数の等式の証明
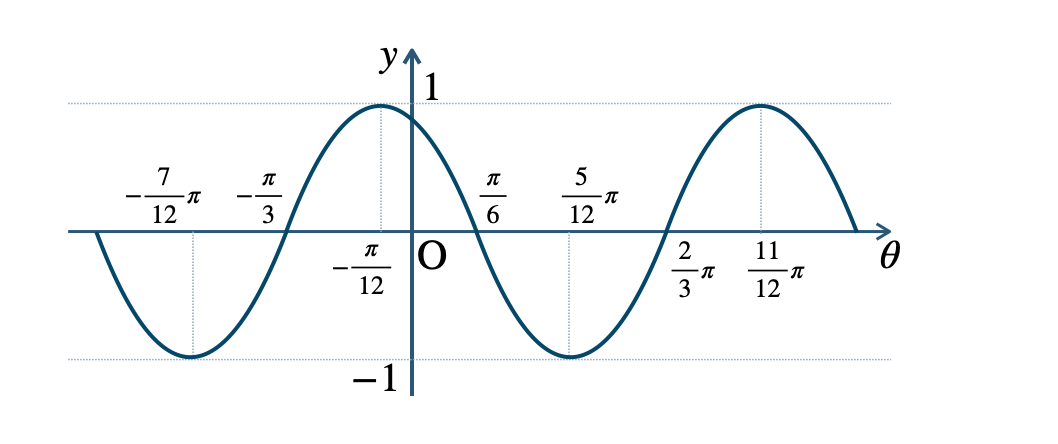
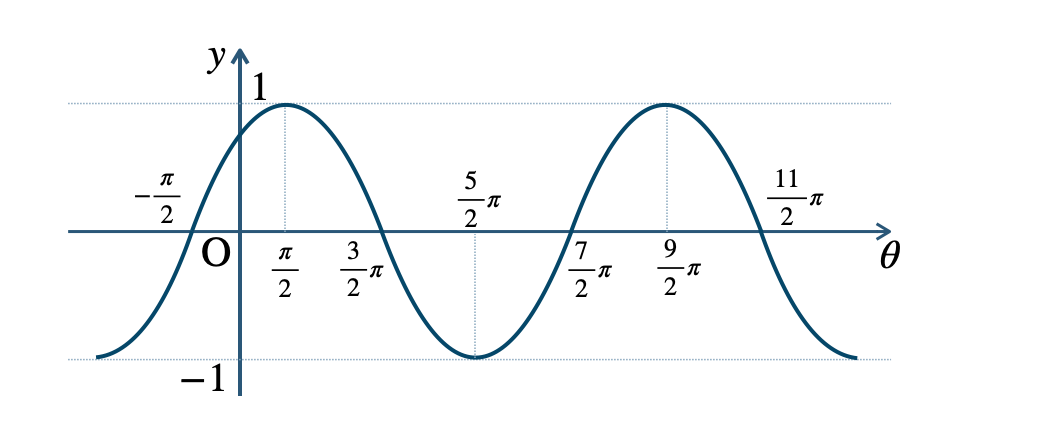
p.125 練習12\({\small (1)}~\)周期 \(2\pi\)



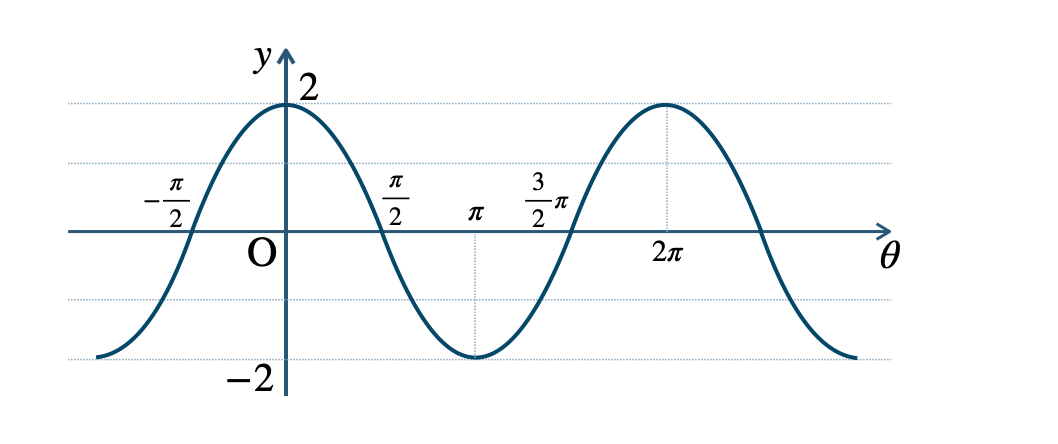
\({\small (2)}~\)周期 \(2\pi\)
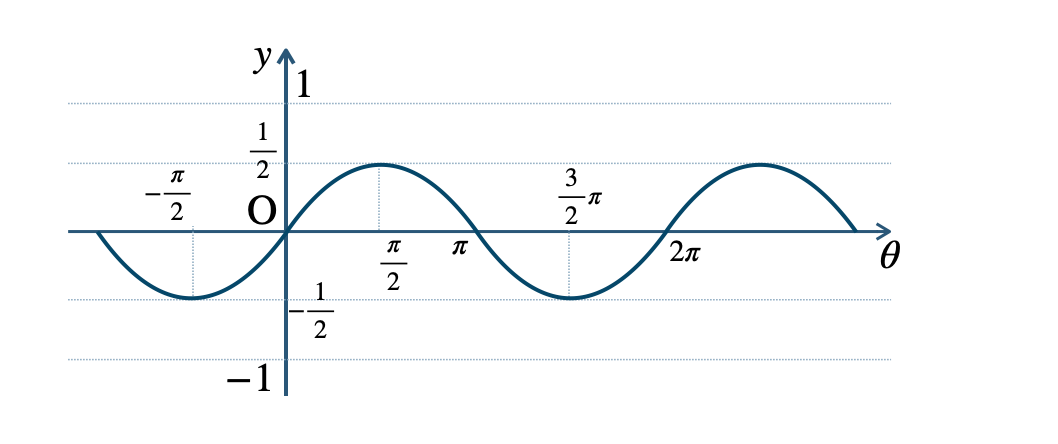
\({\small (3)}~\)周期 \(\pi\)
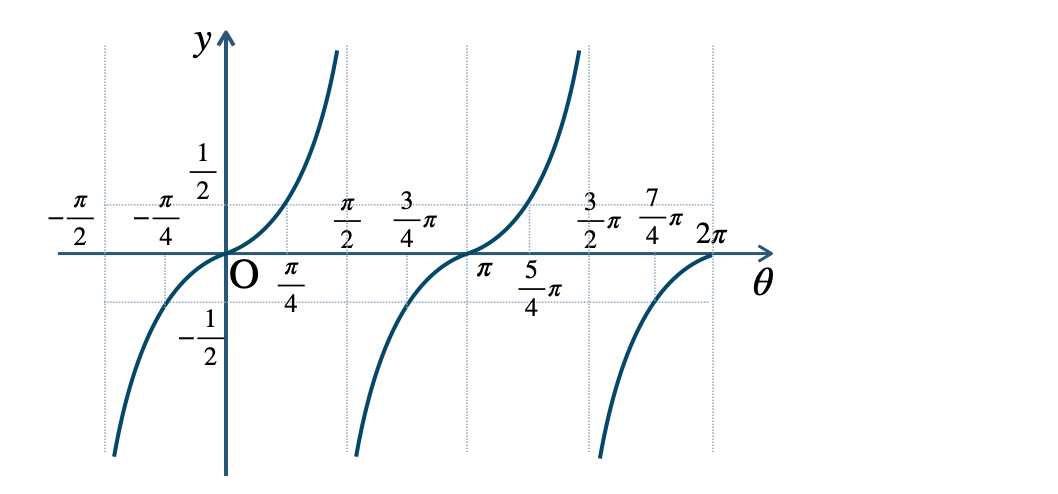
p.125 練習13\({\small (1)}~\)周期 \(2\pi\)



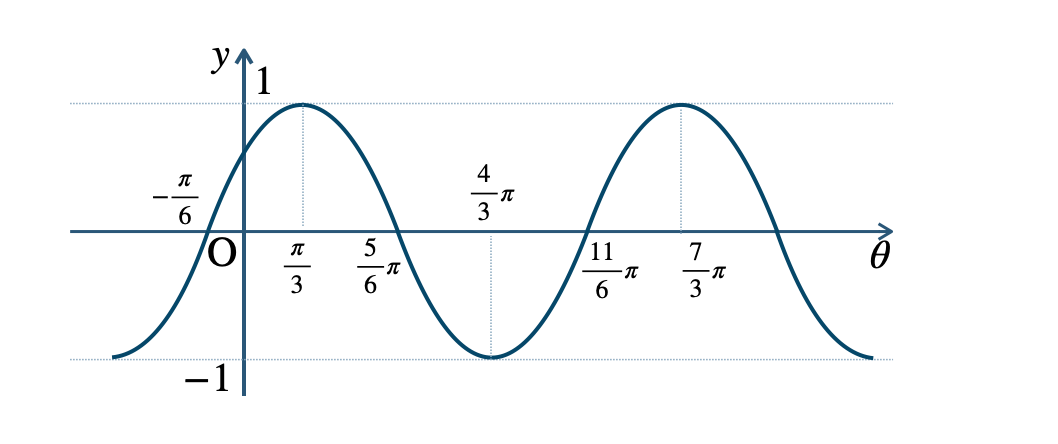
\({\small (2)}~\)周期 \(2\pi\)
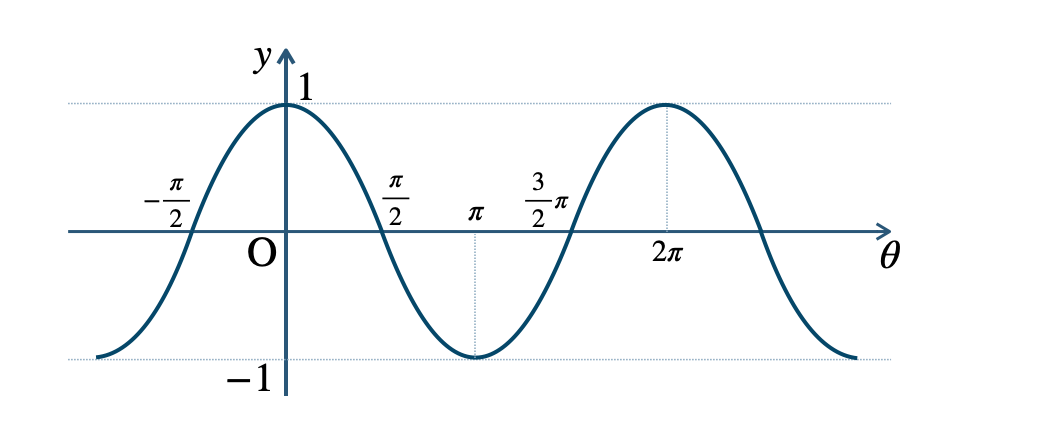
\({\small (3)}~\)周期 \(\pi\)
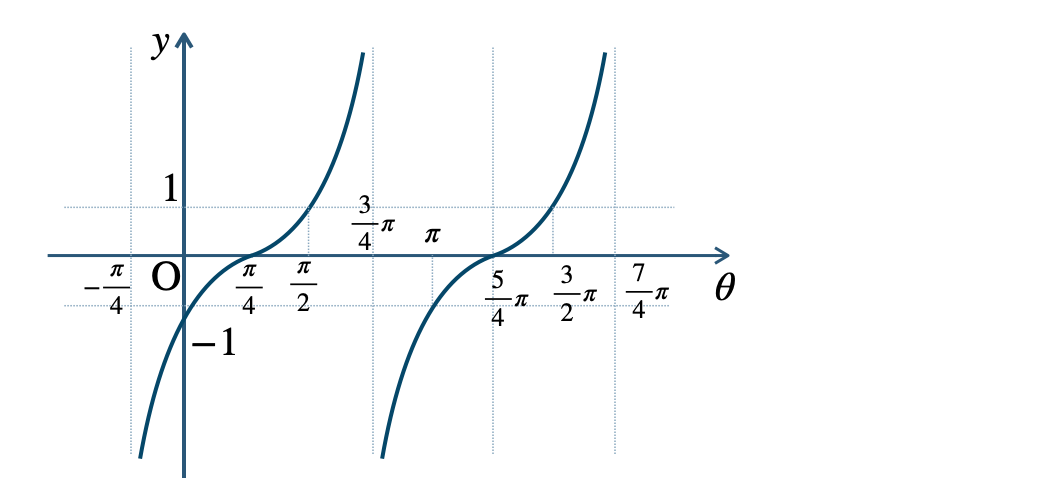
p.126 練習14\({\small (1)}~\)周期 \(\pi\)



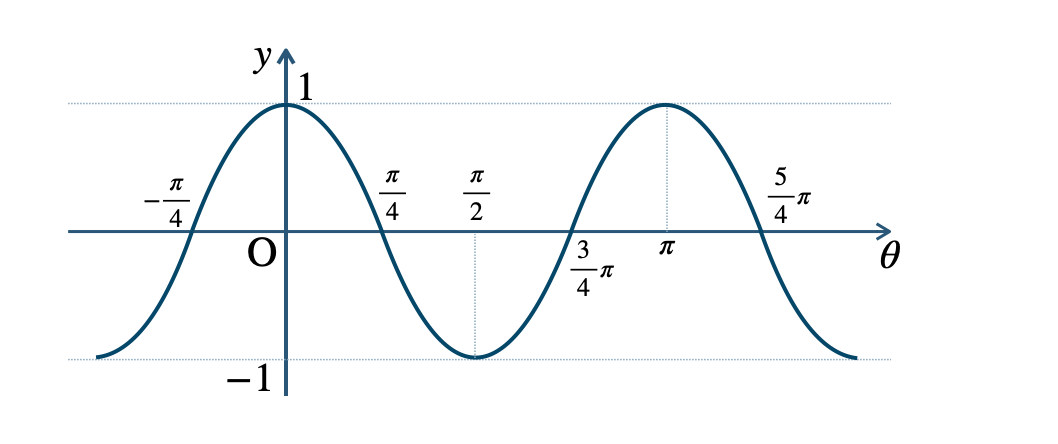
\({\small (2)}~\)周期 \(4\pi\)
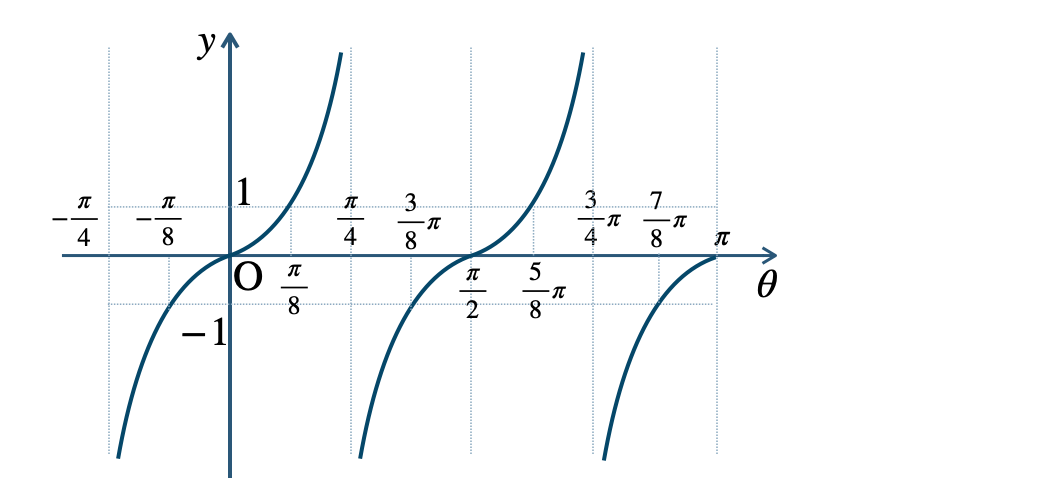
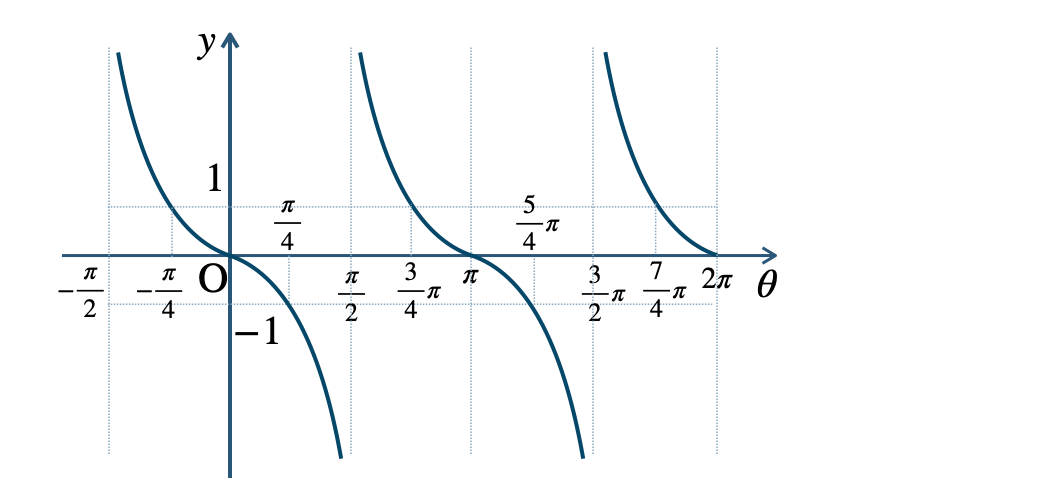
\({\small (3)}~\)周期 \({\large \frac{\,\pi\,}{2}}\)
p.129 練習16$${\small (1)}~-{ \frac{1}{\,2\,}}$$$${\small (2)}~{ \frac{\,\sqrt{3}\,}{2}}$$$${\small (3)}~-1$$→ 三角関数の性質①
→ 三角関数の性質②
→ 三角関数の性質②
p.130 練習17$${\small (1)}~\theta={ \frac{\,\pi\,}{3}}~,~{ \frac{\,2\,}{3}}\pi$$$${\small (2)}~\theta={ \frac{\,2\,}{3}}\pi~,~{ \frac{\,4\,}{3}}\pi$$$${\small (3)}~\theta={ \frac{3}{\,2\,}}\pi$$
p.130 練習18$${\small (1)}~\theta={ \frac{\,4\,}{3}}\pi+2n\pi~,~{ \frac{\,5\,}{3}}\pi+2n\pi$$ ただし、\(n\) は整数$${\small (2)}~\theta={ \frac{3}{\,4\,}}\pi+2n\pi~,~{ \frac{5}{\,4\,}}\pi+2n\pi$$ ただし、\(n\) は整数
p.131 練習19$$~~~\theta={ \frac{\,2\,}{3}}\pi~,~{ \frac{\,5\,}{3}}\pi$$$$~~~\theta={ \frac{\,2\,}{3}}\pi+n\pi$$ ただし、\(n\) は整数
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
p.131 練習20$${\small (1)}~\theta={ \frac{\,17\,}{12}}\pi~,~{ \frac{\,23\,}{12}}\pi$$$${\small (2)}~\theta={ \frac{\,19\,}{12}}\pi~,~{ \frac{\,23\,}{12}}\pi$$→ 三角関数を含む方程式②(範囲変化)
p.132 練習21$${\small (1)}~{ \frac{\,\pi\,}{3}}≦\theta≦{ \frac{\,5\,}{3}}\pi$$$${\small (2)}~{ \frac{\,\pi\,}{4}}<\theta<{ \frac{3}{\,4\,}}\pi$$$${\small (3)}~0≦\theta<{ \frac{\,\pi\,}{6}}~,~{ \frac{5}{\,6\,}}\pi<\theta<2\pi$$
p.133 練習22$$~~~0≦\theta≦{ \frac{\,\pi\,}{3}}~,~{ \frac{\,\pi\,}{2}}<\theta≦{ \frac{\,4\,}{3}}\pi$$$$~~~{ \frac{3}{\,2\,}}\pi<\theta<2\pi$$→ 三角関数を含む不等式①
p.134 練習23 \(\theta=\pi\) で最大値 \(2\)
\(\theta={\large \frac{\,\pi\,}{3}}~,~{\large \frac{\,5\,}{3}}\pi\) で最小値 \(-{\large \frac{1}{\,4\,}}\)
→ 三角関数を含む2次関数
\(\theta={\large \frac{\,\pi\,}{3}}~,~{\large \frac{\,5\,}{3}}\pi\) で最小値 \(-{\large \frac{1}{\,4\,}}\)
→ 三角関数を含む2次関数
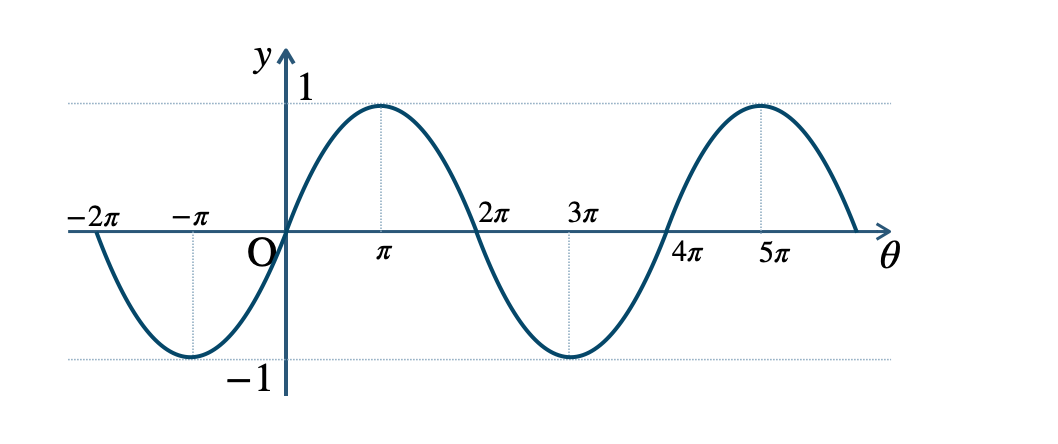
p.135 問題2\({\small (1)}~\)周期 \(\pi\)




\({\small (2)}~\)周期 \(4\pi\)
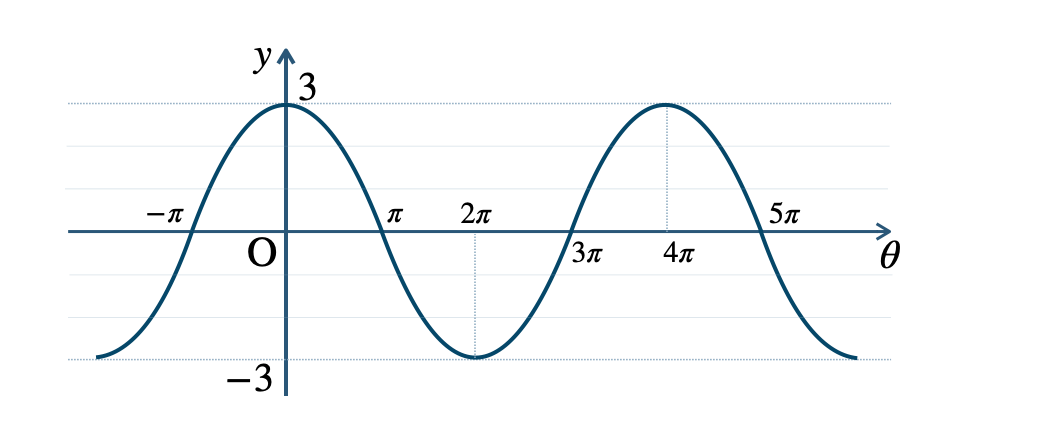
\({\small (3)}~\)周期 \(2\pi\)
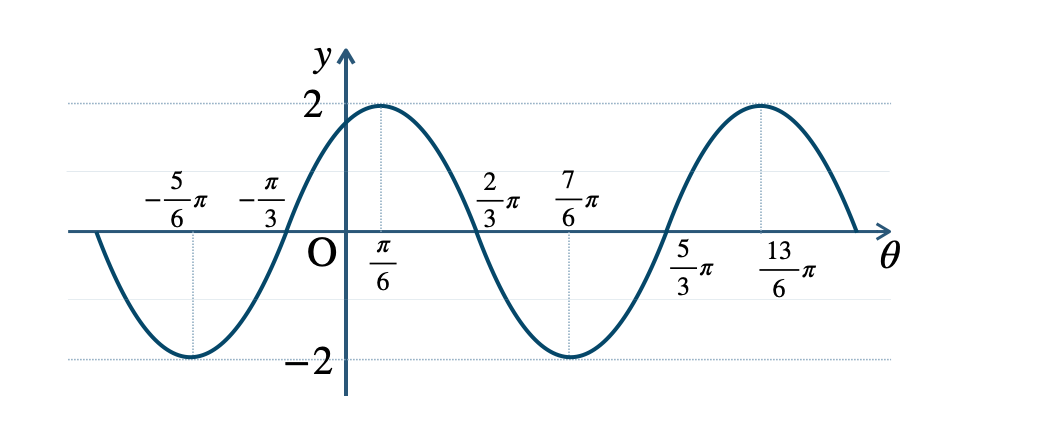
\({\small (4)}~\)周期 \({\large \frac{\,2\,}{3}}\pi\)
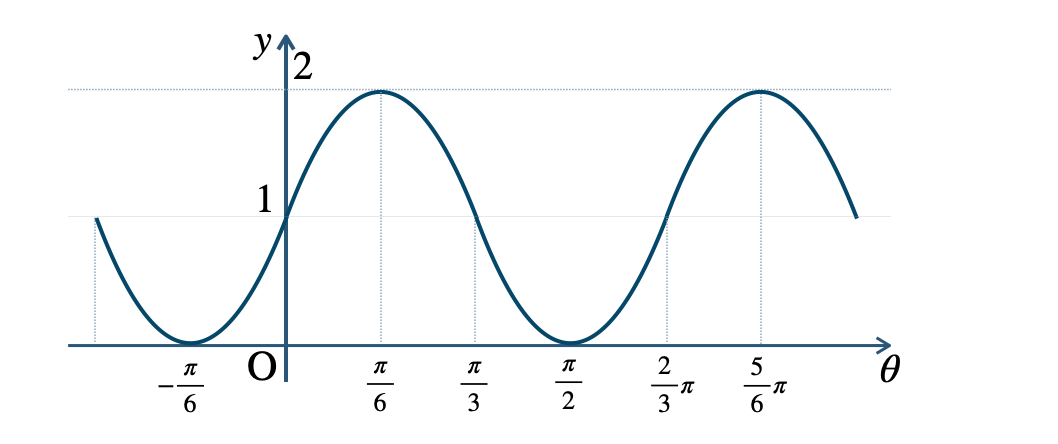
第2節 加法定理
p.137 深める1.$$\begin{eqnarray}~~~&&\sin{(\theta+2n\pi)}\\[2pt]~~~&=&\sin{\theta}\cos{2n\pi}+\cos{\theta}\sin{2n\pi}\\[2pt]~~~&=&\sin{\theta}\times1+\cos{\theta}\times0\\[2pt]~~~&=&\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(\theta+2n\pi)}\\[2pt]~~~&=&\cos{\theta}\cos{2n\pi}-\sin{\theta}\sin{2n\pi}\\[2pt]~~~&=&\cos{\theta}\times1-\sin{\theta}\times0\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
2.$$\begin{eqnarray}~~~&&\sin{(-\theta)}\\[2pt]~~~&=&\sin{(0-\theta)}\\[2pt]~~~&=&\sin{0}\cos{\theta}-\cos{0}\sin{\theta}\\[2pt]~~~&=&0\times \cos{\theta}-1\times\sin{\theta}\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(-\theta)}\\[2pt]~~~&=&\cos{(0-\theta)}\\[2pt]~~~&=&\cos{0}\cos{\theta}-\sin{0}\sin{\theta}\\[2pt]~~~&=&1\times \cos{\theta}-0\times\sin{\theta}\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
3.$$\begin{eqnarray}~~~&&\sin{(\theta+\pi)}\\[2pt]~~~&=&\sin{\theta}\cos{\pi}+\cos{\theta}\sin{\pi}\\[2pt]~~~&=&\sin{\theta}\times(-1)+\cos{\theta}\times0\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(\theta+\pi)}\\[2pt]~~~&=&\cos{\theta}\cos{\pi}-\sin{\theta}\sin{\pi}\\[2pt]~~~&=&\cos{\theta}\times(-1)-\sin{\theta}\times0\\[2pt]~~~&=&-\cos{\theta}\end{eqnarray}$$
4.$$\begin{eqnarray}~~~&&\sin{\left(\theta+\frac{\,\pi\,}{\,2\,}\right)}\\[2pt]~~~&=&\sin{\theta}\cos{\frac{\,\pi\,}{\,2\,}}+\cos{\theta}\sin{\frac{\,\pi\,}{\,2\,}}\\[2pt]~~~&=&\sin{\theta}\times0+\cos{\theta}\times1\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{\left(\theta+\frac{\,\pi\,}{\,2\,}\right)}\\[2pt]~~~&=&\cos{\theta}\cos{\frac{\,\pi\,}{\,2\,}}-\sin{\theta}\sin{\frac{\,\pi\,}{\,2\,}}\\[2pt]~~~&=&\cos{\theta}\times0-\sin{\theta}\times1\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(\theta+2n\pi)}\\[2pt]~~~&=&\cos{\theta}\cos{2n\pi}-\sin{\theta}\sin{2n\pi}\\[2pt]~~~&=&\cos{\theta}\times1-\sin{\theta}\times0\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
2.$$\begin{eqnarray}~~~&&\sin{(-\theta)}\\[2pt]~~~&=&\sin{(0-\theta)}\\[2pt]~~~&=&\sin{0}\cos{\theta}-\cos{0}\sin{\theta}\\[2pt]~~~&=&0\times \cos{\theta}-1\times\sin{\theta}\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(-\theta)}\\[2pt]~~~&=&\cos{(0-\theta)}\\[2pt]~~~&=&\cos{0}\cos{\theta}-\sin{0}\sin{\theta}\\[2pt]~~~&=&1\times \cos{\theta}-0\times\sin{\theta}\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
3.$$\begin{eqnarray}~~~&&\sin{(\theta+\pi)}\\[2pt]~~~&=&\sin{\theta}\cos{\pi}+\cos{\theta}\sin{\pi}\\[2pt]~~~&=&\sin{\theta}\times(-1)+\cos{\theta}\times0\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{(\theta+\pi)}\\[2pt]~~~&=&\cos{\theta}\cos{\pi}-\sin{\theta}\sin{\pi}\\[2pt]~~~&=&\cos{\theta}\times(-1)-\sin{\theta}\times0\\[2pt]~~~&=&-\cos{\theta}\end{eqnarray}$$
4.$$\begin{eqnarray}~~~&&\sin{\left(\theta+\frac{\,\pi\,}{\,2\,}\right)}\\[2pt]~~~&=&\sin{\theta}\cos{\frac{\,\pi\,}{\,2\,}}+\cos{\theta}\sin{\frac{\,\pi\,}{\,2\,}}\\[2pt]~~~&=&\sin{\theta}\times0+\cos{\theta}\times1\\[2pt]~~~&=&\cos{\theta}\end{eqnarray}$$
$$\begin{eqnarray}~~~&&\cos{\left(\theta+\frac{\,\pi\,}{\,2\,}\right)}\\[2pt]~~~&=&\cos{\theta}\cos{\frac{\,\pi\,}{\,2\,}}-\sin{\theta}\sin{\frac{\,\pi\,}{\,2\,}}\\[2pt]~~~&=&\cos{\theta}\times0-\sin{\theta}\times1\\[2pt]~~~&=&-\sin{\theta}\end{eqnarray}$$
p.138 練習24$$~~~{ \frac{\sqrt{6}-\sqrt{\,2\,}}{\,4\,}}$$
p.138 練習25$$~~~{ \frac{\,\sqrt{6}-\sqrt{2}\,}{\,4\,}}~,~{ \frac{\,\sqrt{6}+\sqrt{2}\,}{4}}$$→ 加法定理
p.139 練習26$$~~~{ \frac{\,6+4\sqrt{5}\,}{15}}~,~-{ \frac{\,3\sqrt{5}+8\,}{15}}$$→ 加法定理と式の値
p.139 練習27$$~~~-2-\sqrt{3}$$
p.139 練習28$$~~~2-\sqrt{3}$$
p.140 練習29$$~~~{ \frac{\pi}{4}}$$→ 2直線のなす角
p.141 研究 練習1$$~~~\left({ \frac{\,4\sqrt{3}-3\,}{2}},{ \frac{\,3\sqrt{3}+4\,}{2}}\right)$$
p.142 練習30$${\small (1)}~-{ \frac{\,4\sqrt{5}\,}{9}}$$$${\small (2)}~{ \frac{1}{\,9\,}}$$$${\small (3)}~-4\sqrt{5}$$→ 2倍角の公式
p.142 練習31\({\small (1)}~\) [証明]$$\begin{split}&\sin{3\alpha}\\[2pt]~~=~&\sin{(2\alpha+\alpha)}\\[2pt]~~=~&\sin{2\alpha}\cos{\alpha}+\cos{2\alpha}\sin{\alpha}\\[2pt]~~=~&2\sin{\alpha}\cos^2{\alpha}\\[2pt]~~~~~~&+(1-2\sin^2{\alpha})\sin{\alpha}\\[2pt]~~=~&2\sin{\alpha}(1-\sin^2{\alpha})\\[2pt]~~~~~~&+\sin{\alpha}-2\sin^3{\alpha}\\[2pt]~~=~&=3\sin{\alpha}-4\sin^3{\alpha}\end{split}$$したがって、$$~~~\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}$$[終]
\({\small (2)}~\) [証明]$$\begin{split}&\cos{3\alpha}\\[2pt]~~=~&\cos{(2\alpha+\alpha)}\\[2pt]~~=~&\cos{2\alpha}\cos{\alpha}-\sin{2\alpha}\sin{\alpha}\\[2pt]~~=~&(2\cos^2{\alpha}-1)\cos{\alpha}\\[2pt]~~~~~~&-2\sin^2{\alpha}\cos{\alpha}\\[2pt]~~=~&2\cos^3{\alpha}-\cos{\alpha}\\[2pt]~~~~~~&-2(1-\cos^2{\alpha})\cos{\alpha}\\[2pt]~~=~&4\cos^3{\alpha}-3\cos{\alpha}\end{split}$$したがって、$$~~~\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}$$[終]
\({\small (2)}~\) [証明]$$\begin{split}&\cos{3\alpha}\\[2pt]~~=~&\cos{(2\alpha+\alpha)}\\[2pt]~~=~&\cos{2\alpha}\cos{\alpha}-\sin{2\alpha}\sin{\alpha}\\[2pt]~~=~&(2\cos^2{\alpha}-1)\cos{\alpha}\\[2pt]~~~~~~&-2\sin^2{\alpha}\cos{\alpha}\\[2pt]~~=~&2\cos^3{\alpha}-\cos{\alpha}\\[2pt]~~~~~~&-2(1-\cos^2{\alpha})\cos{\alpha}\\[2pt]~~=~&4\cos^3{\alpha}-3\cos{\alpha}\end{split}$$したがって、$$~~~\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}$$[終]
p.143 練習32$${\small (1)}~{ \frac{\,\sqrt{2-\sqrt{2}}\,}{2}}$$$${\small (2)}~{ \frac{\,\sqrt{2+\sqrt{2}}\,}{2}}$$$${\small (3)}~{ \frac{\,\sqrt{2-\sqrt{2}}\,}{2}}$$
p.143 練習33$${\small (1)}~{ \frac{3}{\,\sqrt{10}\,}}$$$${\small (2)}~{ \frac{1}{\,\sqrt{10}\,}}$$$${\small (3)}~3$$→ 半角の公式
p.144 練習34$${\small (1)}~\theta=0~,~{ \frac{\,\pi\,}{6}}~,~{ \frac{5}{\,6\,}}\pi~,~\pi$$$${\small (2)}~0<\theta<{ \frac{\,\pi\,}{6}}~,~{ \frac{5}{\,6\,}}\pi<\theta<\pi$$→ 2倍角を含む方程式・不等式
p.145 練習35$${\small (1)}~2\sin{\left(\theta+{ \frac{\,\pi\,}{6}}\right)}$$$${\small (2)}~\sqrt{2}\sin{\left(\theta-{ \frac{\,\pi\,}{4}}\right)}$$→ 三角関数の合成
p.146 練習36$$~~~x={ \frac{\,\pi\,}{2}}~,~{ \frac{\,11\,}{6}}\pi$$→ 合成を用いる方程式と不等式
p.147 練習37 \(x={\large \frac{\,\pi\,}{\,3\,}}\) のとき、最大値 \(2\)
\(x={\large \frac{\,4\,}{\,3\,}}\pi\) のとき、最小値 \(-2\)
→ 三角関数の最大値・最小値
\(x={\large \frac{\,4\,}{\,3\,}}\pi\) のとき、最小値 \(-2\)
→ 三角関数の最大値・最小値
p.147 深める\(\sin{x}=1~,~\cos{x}=1\) を同時に満たす \(x\) は存在しないので、\(y\) の最大値は \(2\) とならない
また、最小値でも同様に考える
また、最小値でも同様に考える
問題
p.149 問題 8\({\small (1)}~\)[証明]
(左辺)$$=(\sin{\alpha}+\cos{\alpha})^2$$$$=\sin^2{\alpha}+2\sin{\alpha}\cos{\alpha}+\cos^2{\alpha}$$$$=1+2\sin{\alpha}\cos{\alpha}$$ (右辺)$$=1+\sin{2\alpha}$$$$=1+2\sin{\alpha}\cos{\alpha}$$したがって、$$~~~(\sin{\alpha}+\cos{\alpha})^2=1+\sin{2\alpha}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$=\frac{\sin{2\alpha}}{\,1+\cos{2\alpha}\,}$$$$=\frac{2\sin{\alpha}\cos{\alpha}}{\,1+2\cos^2{\alpha}-1\,}$$$$=\frac{\,2\sin{\alpha}\cos{\alpha}\,}{2\cos^2{\alpha}}$$$$=\frac{\,\sin{\alpha}\,}{\cos{\alpha}}$$$$=\tan{\alpha}$$したがって、$$~~~\frac{\sin{2\alpha}}{1+\cos{2\alpha}}=\tan{\alpha}$$[終
(左辺)$$=(\sin{\alpha}+\cos{\alpha})^2$$$$=\sin^2{\alpha}+2\sin{\alpha}\cos{\alpha}+\cos^2{\alpha}$$$$=1+2\sin{\alpha}\cos{\alpha}$$ (右辺)$$=1+\sin{2\alpha}$$$$=1+2\sin{\alpha}\cos{\alpha}$$したがって、$$~~~(\sin{\alpha}+\cos{\alpha})^2=1+\sin{2\alpha}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$=\frac{\sin{2\alpha}}{\,1+\cos{2\alpha}\,}$$$$=\frac{2\sin{\alpha}\cos{\alpha}}{\,1+2\cos^2{\alpha}-1\,}$$$$=\frac{\,2\sin{\alpha}\cos{\alpha}\,}{2\cos^2{\alpha}}$$$$=\frac{\,\sin{\alpha}\,}{\cos{\alpha}}$$$$=\tan{\alpha}$$したがって、$$~~~\frac{\sin{2\alpha}}{1+\cos{2\alpha}}=\tan{\alpha}$$[終
章末問題 三角関数
章末問題A
p.150 章末問題A 3\({\small (1)}~\)[証明]
(左辺)$$=\frac{1}{\,1+\cos{\theta}\,}+\frac{1}{\,1-\cos{\theta}\,}$$$$=\frac{\,1-\cos{\theta}+1+\cos{\theta}\,}{\,(1+\cos{\theta})(1-\cos{\theta})\,}$$$$=\frac{2}{\,1-\cos^2{\theta}\,}$$$$=\frac{2}{\,\sin^2{\theta}\,}$$したがって、$$~~~\frac{1}{\,1+\cos{\theta}\,}+\frac{1}{\,1-\cos{\theta}\,}=\frac{2}{\,\sin^2{\theta}\,}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$=\frac{1}{\,\tan{\theta}\,}-\tan{\theta}$$$$=\frac{\,\cos{\theta}\,}{\sin{\theta}}-\frac{\,\sin{\theta}\,}{\cos{\theta}}$$$$=\frac{\,\cos^2{\theta}-\sin^2{\theta}\,}{\sin{\theta}\cos{\theta}}$$ (右辺)$$=\frac{\,2\cos{2\theta}\,}{\sin{2\theta}}$$$$=\frac{\,2(\cos^2{\theta}-\sin^2{\theta})\,}{\,2\sin{\theta}\cos{\theta}\,}$$$$=\frac{\,\cos^2{\theta}-\sin^2{\theta}\,}{\sin{\theta}\cos{\theta}}$$したがって、$$~~~\frac{1}{\,\tan{\theta}\,}-\tan{\theta}=\frac{\,2\cos{2\theta}\,}{\sin{2\theta}}$$[終]
(左辺)$$=\frac{1}{\,1+\cos{\theta}\,}+\frac{1}{\,1-\cos{\theta}\,}$$$$=\frac{\,1-\cos{\theta}+1+\cos{\theta}\,}{\,(1+\cos{\theta})(1-\cos{\theta})\,}$$$$=\frac{2}{\,1-\cos^2{\theta}\,}$$$$=\frac{2}{\,\sin^2{\theta}\,}$$したがって、$$~~~\frac{1}{\,1+\cos{\theta}\,}+\frac{1}{\,1-\cos{\theta}\,}=\frac{2}{\,\sin^2{\theta}\,}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$=\frac{1}{\,\tan{\theta}\,}-\tan{\theta}$$$$=\frac{\,\cos{\theta}\,}{\sin{\theta}}-\frac{\,\sin{\theta}\,}{\cos{\theta}}$$$$=\frac{\,\cos^2{\theta}-\sin^2{\theta}\,}{\sin{\theta}\cos{\theta}}$$ (右辺)$$=\frac{\,2\cos{2\theta}\,}{\sin{2\theta}}$$$$=\frac{\,2(\cos^2{\theta}-\sin^2{\theta})\,}{\,2\sin{\theta}\cos{\theta}\,}$$$$=\frac{\,\cos^2{\theta}-\sin^2{\theta}\,}{\sin{\theta}\cos{\theta}}$$したがって、$$~~~\frac{1}{\,\tan{\theta}\,}-\tan{\theta}=\frac{\,2\cos{2\theta}\,}{\sin{2\theta}}$$[終]
p.150 章末問題A 5\({\small (1)}~\)$$~~~~~\sin{(\pi-\theta)}$$$$~=\sin{\pi}\cos{\theta}-\cos{\pi}\sin{\theta}$$$$~=0\cdot\cos{\theta}-(-1)\cdot\sin{\theta}$$$$=\sin{\theta}$$
$$~~~~~~\cos{(\pi-\theta)}$$$$~=\cos{\pi}\cos{\theta}+\sin{\pi}\sin{\theta}$$$$~=(-1)\cdot\cos{\theta}+0\cdot\sin{\theta}=-\cos{\theta}$$
$$~~~~~~\tan{(\pi-\theta)}$$$$~=\frac{\tan{\pi}-\tan{\theta}}{1+\tan{\pi}\tan{\theta}}$$$$~=\frac{0-\tan{\theta}}{1+0\cdot\tan{\theta}}$$$$=-\tan{\theta}$$
\({\small (2)}~\)$$~~~~~\sin{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\sin{\frac{\,\pi\,}{2}}\cos{\theta}-\cos{\frac{\,\pi\,}{2}}\sin{\theta}$$$$~=1\cdot\cos{\theta}-0\cdot\sin{\theta}$$$$=\cos{\theta}$$
$$~~~~~~\cos{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\cos{\frac{\,\pi\,}{2}}\cos{\theta}+\sin{\frac{\,\pi\,}{2}}\sin{\theta}$$$$~=0\cdot\cos{\theta}+1\cdot\sin{\theta}=\sin{\theta}$$
$$~~~~~~\tan{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\frac{\sin{\left(\frac{\,\pi\,}{2}-\theta\right)}}{\cos{\left(\frac{\,\pi\,}{2}-\theta\right)}}$$$$~=\frac{\cos{\theta}}{\sin{\theta}}$$$$~=\frac{1}{\tan{\theta}}$$
$$~~~~~~\cos{(\pi-\theta)}$$$$~=\cos{\pi}\cos{\theta}+\sin{\pi}\sin{\theta}$$$$~=(-1)\cdot\cos{\theta}+0\cdot\sin{\theta}=-\cos{\theta}$$
$$~~~~~~\tan{(\pi-\theta)}$$$$~=\frac{\tan{\pi}-\tan{\theta}}{1+\tan{\pi}\tan{\theta}}$$$$~=\frac{0-\tan{\theta}}{1+0\cdot\tan{\theta}}$$$$=-\tan{\theta}$$
\({\small (2)}~\)$$~~~~~\sin{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\sin{\frac{\,\pi\,}{2}}\cos{\theta}-\cos{\frac{\,\pi\,}{2}}\sin{\theta}$$$$~=1\cdot\cos{\theta}-0\cdot\sin{\theta}$$$$=\cos{\theta}$$
$$~~~~~~\cos{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\cos{\frac{\,\pi\,}{2}}\cos{\theta}+\sin{\frac{\,\pi\,}{2}}\sin{\theta}$$$$~=0\cdot\cos{\theta}+1\cdot\sin{\theta}=\sin{\theta}$$
$$~~~~~~\tan{\left(\frac{\,\pi\,}{2}-\theta\right)}$$$$~=\frac{\sin{\left(\frac{\,\pi\,}{2}-\theta\right)}}{\cos{\left(\frac{\,\pi\,}{2}-\theta\right)}}$$$$~=\frac{\cos{\theta}}{\sin{\theta}}$$$$~=\frac{1}{\tan{\theta}}$$
p.151 章末問題B 9
[証明]
(左辺)$$~=\frac{\,\sin{(\alpha-\beta)}\,}{\sin{(\alpha+\beta)}}$$$$~=\frac{\,\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\,}{\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}}$$両辺を \(\cos{\alpha}\cos{\beta}\) で割ると、$$~=\frac{\,\frac{\,\sin{\alpha}\,}{\cos{\alpha}}-\frac{\,\sin{\beta}\,}{\cos{\beta}}\,}{\frac{\,\sin{\alpha}\,}{\cos{\alpha}}+\frac{\,\sin{\beta}\,}{\cos{\beta}}}$$$$~=\frac{\,\tan{\alpha}-\tan{\beta}\,}{\tan{\alpha}+\tan{\beta}}$$したがって、$$~~~\frac{\,\sin{(\alpha-\beta)}\,}{\sin{(\alpha+\beta)}}=\frac{\,\tan{\alpha}-\tan{\beta}\,}{\tan{\alpha}+\tan{\beta}}$$[終]
[証明]
(左辺)$$~=\frac{\,\sin{(\alpha-\beta)}\,}{\sin{(\alpha+\beta)}}$$$$~=\frac{\,\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\,}{\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}}$$両辺を \(\cos{\alpha}\cos{\beta}\) で割ると、$$~=\frac{\,\frac{\,\sin{\alpha}\,}{\cos{\alpha}}-\frac{\,\sin{\beta}\,}{\cos{\beta}}\,}{\frac{\,\sin{\alpha}\,}{\cos{\alpha}}+\frac{\,\sin{\beta}\,}{\cos{\beta}}}$$$$~=\frac{\,\tan{\alpha}-\tan{\beta}\,}{\tan{\alpha}+\tan{\beta}}$$したがって、$$~~~\frac{\,\sin{(\alpha-\beta)}\,}{\sin{(\alpha+\beta)}}=\frac{\,\tan{\alpha}-\tan{\beta}\,}{\tan{\alpha}+\tan{\beta}}$$[終]
p.151 章末問題B 11\({\small (1)}~\)周期 \(\pi\)


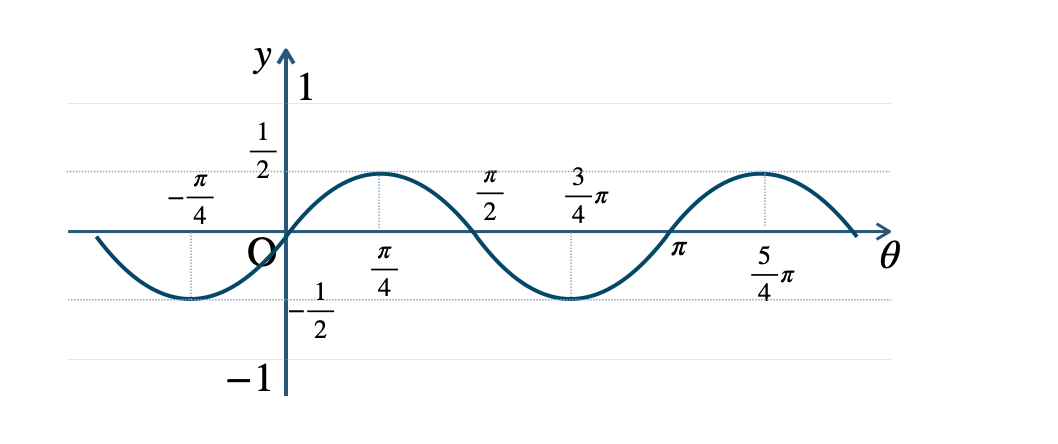
\({\small (2)}~\)周期 \(\pi\)
次のページ「第5章 指数関数と対数関数」