このページは、数研出版:数学Ⅰ[712]
第4章 図形と計量
第4章 図形と計量

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版数学Ⅰ 第1章 数と式
数研出版数学Ⅰ 第2章 集合と命題
数研出版数学Ⅰ 第3章 2次関数
数研出版数学Ⅰ 第4章 図形と計量
数研出版数学Ⅰ 第5章 データの分析
第4章 図形と計量
第1節 三角比
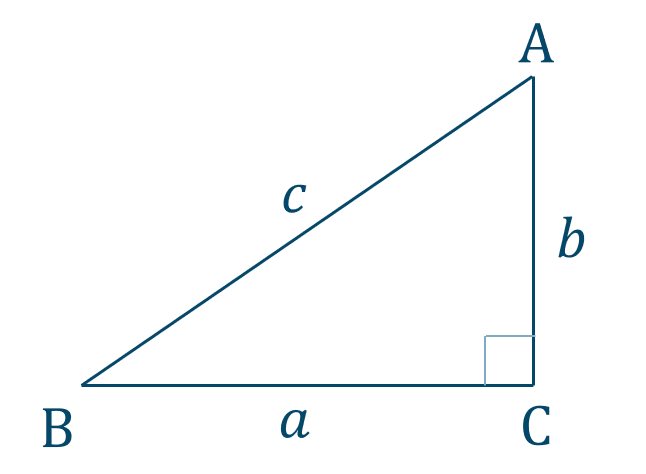
p.135 練習1$${\small (1)}~\sin{\theta}={ \frac{\,1\,}{\,\sqrt{5}\,}}~,~\cos{\theta}={ \frac{\,2\,}{\,\sqrt{5}\,}}$$$$~~~~~~\tan{\theta}={ \frac{\,1\,}{\,2\,}}$$$${\small (2)}~\sin{\theta}={ \frac{\,5\,}{\,13\,}}~,~\cos{\theta}={ \frac{\,12\,}{\,13\,}}$$$$~~~~~~\tan{\theta}={ \frac{\,5\,}{\,12\,}}$$$${\small (3)}~\sin{\theta}={ \frac{\,\sqrt{3}\,}{\,2\,}}~,~\cos{\theta}={ \frac{\,1\,}{\,2\,}}$$$$~~~~~~\tan{\theta}=\sqrt{3}$$→ 直角三角形と三角比
p.136 練習2$${\small (1)}~\cos{30^\circ}={ \frac{\sqrt{\,3\,}}{\,2\,}}~,~\tan{30^\circ}={ \frac{\,1\,}{\,\sqrt{3}\,}}$$$${\small (2)}~\sin{45^\circ}={ \frac{\,1\,}{\,\sqrt{2}\,}}~,~\tan{45^\circ}=1$$$${\small (3)}~\sin{60^\circ}={ \frac{\,\sqrt{3}\,}{\,2\,}}~,~\cos{60^\circ}={ \frac{\,1\,}{\,2\,}}$$→ 三角比の値(鋭角)
p.136 練習3$${\small (1)}~0.4067$$$${\small (2)}~0.1219$$$${\small (3)}~2.2460$$
p.136 練習4$${\small (1)}~15^\circ$$$${\small (2)}~58^\circ$$$${\small (3)}~77^\circ$$
p.137 練習5 鉛直方向 \(171\) m、水平方向 \(470\) m
p.138 練習6$$~~~26.8~{\rm m}$$
p.138 問1 約 \(5\) 度
p.138 練習7 約 \(6\) 度
p.140 練習8$${\small (1)}~\cos{\theta}={ \frac{\,\sqrt{21}\,}{\,5\,}}~,~\tan{\theta}={ \frac{\,2\sqrt{21}\,}{\,21\,}}$$$${\small (2)}~\sin{\theta}={ \frac{\,\sqrt{7}\,}{\,4\,}}~,~\tan{\theta}={ \frac{\,\sqrt{7}\,}{\,3\,}}$$
p.140 練習9$$~~~\cos{\theta}={ \frac{\,2\sqrt{5}\,}{\,5\,}}~,~\sin{\theta}={ \frac{\,\sqrt{5}\,}{\,5\,}}$$→ 三角比の相互関係の公式(鋭角)
p.141 練習10$${\small (1)}~\cos{16^\circ}$$$${\small (2)}~\sin{41^\circ}$$$${\small (3)}~{ \frac{\,1\,}{\,\tan{25^\circ}\,}}$$→ 余角の公式
p.141 問2[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\sin{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\sin{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\cos{{\frac{\,{\rm B+C}\,}{\,2\,}}}\end{split}$$[終]
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\sin{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\sin{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\cos{{\frac{\,{\rm B+C}\,}{\,2\,}}}\end{split}$$[終]
p.141 練習11\({\small (1)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\cos{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\cos{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\sin{{\frac{\,{\rm B+C}\,}{\,2\,}}}\end{split}$$[終]
\({\small (2)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\tan{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\tan{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\frac{\,1\,}{\,\tan{{\frac{\,{\rm B+C}\,}{\,2\,}}}\,}\end{split}$$したがって、$$~~~\tan{{\frac{\,{\rm A}\,}{\,2\,}}} \tan{{\frac{\,{\rm B+C}\,}{\,2\,}}}=1$$[終]
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\cos{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\cos{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\sin{{\frac{\,{\rm B+C}\,}{\,2\,}}}\end{split}$$[終]
\({\small (2)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$$~~~~{\frac{\,\rm A\,}{\,2\,}}=90^\circ-{\frac{\,\rm B+C\,}{\,2\,}}$$これより、$$\begin{split}&\tan{{\frac{\,{\rm A}\,}{\,2\,}}}\\[3pt]~~=~&\tan{\left(90^\circ-{\frac{\,{\rm B+C}\,}{\,2\,}}\right)}\\[3pt]~~=~&\frac{\,1\,}{\,\tan{{\frac{\,{\rm B+C}\,}{\,2\,}}}\,}\end{split}$$したがって、$$~~~\tan{{\frac{\,{\rm A}\,}{\,2\,}}} \tan{{\frac{\,{\rm B+C}\,}{\,2\,}}}=1$$[終]
p.143 練習12$${\small (1)}~\sin{135^\circ}={ \frac{\,1\,}{\,\sqrt{2}\,}}~,~\cos{135^\circ}=-{ \frac{\,1\,}{\,\sqrt{2}\,}}$$$$~~~~~~\tan{135^\circ}=-1$$$${\small (2)}~\sin{150^\circ}={ \frac{\,1\,}{\,2\,}}~,~\cos{150^\circ}=-{ \frac{\,\sqrt{3}\,}{\,2\,}}$$$$~~~~~~\tan{150^\circ}=-{ \frac{\,1\,}{\,\sqrt{3}\,}}$$→ 三角比の拡張
p.145 深める\(\sin{\theta}\) の値は、
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(0\) から \(1\) まで大きくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは \(1\) から \(0\) まで小さくなる
\(\cos{\theta}\) の値は、
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(1\) から \(0\) まで小さくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは \(0\) から \(-1\) まで小さくなる
\(\tan{\theta}\) の値は、
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(0\) から限りなく大きくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは限りなく小さい値から \(0\) まで大きくなる
(ただし、\(\theta=90^\circ\) にはならない)
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(0\) から \(1\) まで大きくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは \(1\) から \(0\) まで小さくなる
\(\cos{\theta}\) の値は、
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(1\) から \(0\) まで小さくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは \(0\) から \(-1\) まで小さくなる
\(\tan{\theta}\) の値は、
\(\theta\) が \(0^\circ \to 90^\circ\) のときは \(0\) から限りなく大きくなる
\(\theta\) が \(90^\circ \to 180^\circ\) のときは限りなく小さい値から \(0\) まで大きくなる
(ただし、\(\theta=90^\circ\) にはならない)
p.146 練習13$${\small (1)}~0.1736$$$${\small (2)}~-0.9205$$$${\small (3)}~-1.1918$$→ 補角の公式
p.147 練習14$${\small (1)}~45^\circ~,~135^\circ$$$${\small (2)}~30^\circ$$$${\small (3)}~120^\circ$$$${\small (4)}~0^\circ~,~180^\circ$$
p.148 練習15$${\small (1)}~45^\circ$$$${\small (2)}~150^\circ$$→ 三角比と方程式
p.149 練習16\({\small (1)}~0^\circ≦\theta≦90^\circ\) のとき$$~~~\cos{\theta}={ \frac{\,\sqrt{5}\,}{\,3\,}}~,~\tan{\theta}={ \frac{\,2\sqrt{5}\,}{\,5\,}}$$\(90^\circ≦\theta≦180^\circ\) のとき$$~~~\cos{\theta}=-{ \frac{\,\sqrt{5}\,}{\,3\,}}~,~\tan{\theta}=-{ \frac{\,2\sqrt{5}\,}{\,5\,}}$$\({\small (2)}\)$$~~~\sin{\theta}={ \frac{\,\sqrt{15}\,}{\,4\,}}~,~\tan{\theta}=-\sqrt{15}$$
p.149 問3$$~~~\cos{\theta}=-{ \frac{\,\sqrt{5}\,}{\,5\,}}~,~\sin{\theta}={ \frac{\,2\sqrt{5}\,}{\,5\,}}$$
p.149 練習17$${\small (1)}~\cos{\theta}=-{ \frac{\,\sqrt{3}\,}{\,3\,}}~,~\sin{\theta}={ \frac{\,\sqrt{6}\,}{\,3\,}}$$$${\small (2)}~\cos{\theta}={ \frac{\,3\sqrt{10}\,}{\,10\,}}~,~\sin{\theta}={ \frac{\,\sqrt{10}\,}{\,10\,}}$$→ 三角比の相互関係の公式(鈍角)
p.150 練習18$${\small (1)}~45^\circ$$$${\small (2)}~120^\circ$$→ 直線の傾きと正接