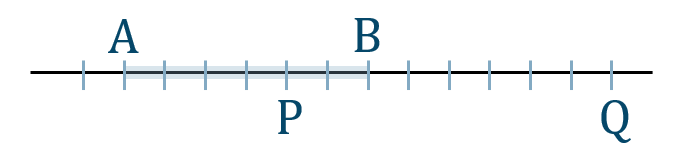文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第2章 図形の性質
第1節 平面図形
p.66
練習2
\({\small (1)}~5:3\) \({\small (2)}~{\Large \frac{15}{2}}\)
練習2
\({\small (1)}~5:3\) \({\small (2)}~{\Large \frac{15}{2}}\)
p.66
練習3
[証明]

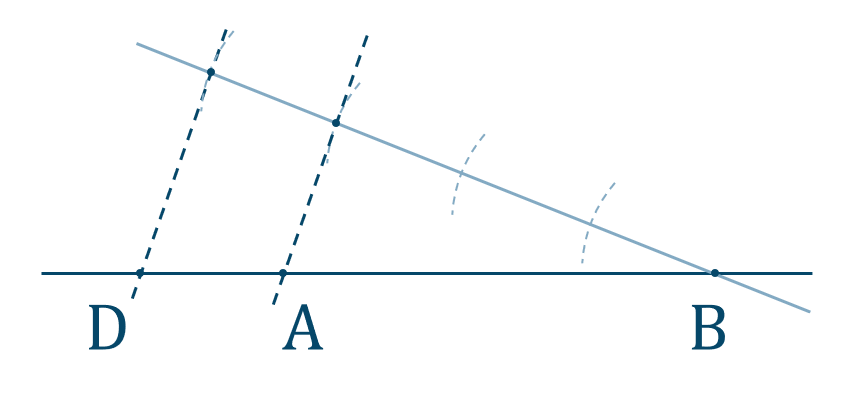
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\parallel EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\parallel EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
練習3
[証明]
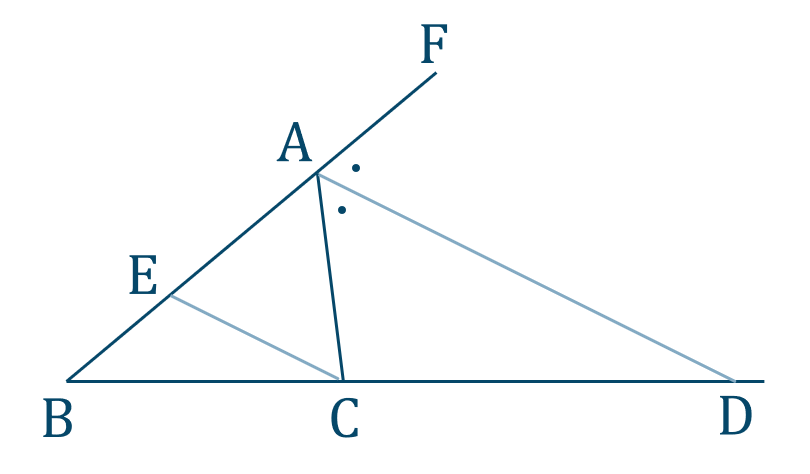
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AD\parallel EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAD}=\angle{\rm CAD}\) …①
の同位角より、
\(\angle{\rm FAD}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAD}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AD\parallel EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CD}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BD}:{\rm DC}={\rm AB}:{\rm AC}\) [終]
p.68
練習5
\({\small (1)}~20^{\circ}\) \({\small (2)}~100^{\circ}\) \({\small (3)}~20^{\circ}\)
→ 三角形の外心
練習5
\({\small (1)}~20^{\circ}\) \({\small (2)}~100^{\circ}\) \({\small (3)}~20^{\circ}\)
→ 三角形の外心
p.70
練習6
\({\small (1)}~30^{\circ}\) \({\small (2)}~25^{\circ}\) \({\small (3)}~110^{\circ}\)
→ 三角形の内心
練習6
\({\small (1)}~30^{\circ}\) \({\small (2)}~25^{\circ}\) \({\small (3)}~110^{\circ}\)
→ 三角形の内心
p.71
練習7
\({\small (1)}~5\) \({\small (2)}~4\)
練習7
\({\small (1)}~5\) \({\small (2)}~4\)
p.73
練習9
\(3:2\)
練習9
\(3:2\)
p.75
練習12
\({\small (1)}~1:1\) \({\small (2)}~3:5\)
練習12
\({\small (1)}~1:1\) \({\small (2)}~3:5\)
p.77
研究2
[証明] \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) において、
他の角は \(\angle{\rm C}\) より小さい鋭角であるので、
\(\angle{\rm C}>\angle{\rm A}~,~\angle{\rm C}>\angle{\rm B}\)
三角形の辺と角の大小関係より、
\(c>a~,~c>b\)
したがって、\(c\) が最大の辺となるので、直角三角形では3辺のうち斜辺が最大である [終]
研究2
[証明] \(\angle{\rm C}=90^\circ\) の直角三角形 \(\triangle {\rm ABC}\) において、
他の角は \(\angle{\rm C}\) より小さい鋭角であるので、
\(\angle{\rm C}>\angle{\rm A}~,~\angle{\rm C}>\angle{\rm B}\)
三角形の辺と角の大小関係より、
\(c>a~,~c>b\)
したがって、\(c\) が最大の辺となるので、直角三角形では3辺のうち斜辺が最大である [終]
p.78
練習14
\({\small (1)}\)
対頂角より、
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)
\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
練習14
\({\small (1)}\)
対頂角より、
\(\angle{\rm DEC}=\angle{\rm AEB}=78^{\circ}\)
\(\triangle{\rm DEC}\) の内角の和より、
\(\angle{\rm DEC}=180^{\circ}-(78^{\circ}+37^{\circ})=65^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm CDB}=65^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
\({\small (2)}\)
\(\triangle{\rm EBD}\) の外角の関係より、
\(\angle{\rm BDC}=\angle{\rm BED}+\angle{\rm EBD}\)
角度より、
\(\angle{\rm BDC}=84^{\circ}+26^{\circ}=110^{\circ}\)
よって、\(\angle{\rm BAC}=\angle{\rm BDC}=110^{\circ}\)
したがって、4点 \({\rm A,B,C,D}\) は1つの円周上にある
p.81
練習16
②、③
練習16
②、③
p.81
練習17
[証明]

図のように、線分 \({\rm AB}\) を延ばした点を \({\rm E}\) とすると、
\({\rm AD\parallel BC}\) より、同位角が等しいので、
\(\angle{\rm ABC}=\angle{\rm EAD}\)
ここで、\(\angle{\rm ABC}=\angle{\rm BCD}\) より、
\(\angle{\rm EAD}=\angle{\rm BCD}\)
したがって、内角がその対角の外角に等しいので台形 \({\rm ABCD}\) は円に内接する [終]
練習17
[証明]
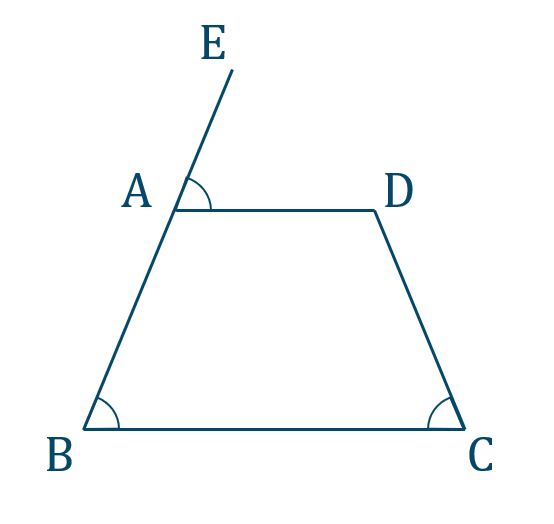
図のように、線分 \({\rm AB}\) を延ばした点を \({\rm E}\) とすると、
\({\rm AD\parallel BC}\) より、同位角が等しいので、
\(\angle{\rm ABC}=\angle{\rm EAD}\)
ここで、\(\angle{\rm ABC}=\angle{\rm BCD}\) より、
\(\angle{\rm EAD}=\angle{\rm BCD}\)
したがって、内角がその対角の外角に等しいので台形 \({\rm ABCD}\) は円に内接する [終]
p.84
練習19
[証明]
直角の場合
\(\angle{\rm BAT}=90^\circ\)
直径に対する円周角は \(90^\circ\) より、
\(\angle{\rm APB}=90^\circ\)
したがって、
\(\angle{\rm BAT}=\angle{\rm APB}\)
練習19
[証明]
直角の場合
\(\angle{\rm BAT}=90^\circ\)
直径に対する円周角は \(90^\circ\) より、
\(\angle{\rm APB}=90^\circ\)
したがって、
\(\angle{\rm BAT}=\angle{\rm APB}\)
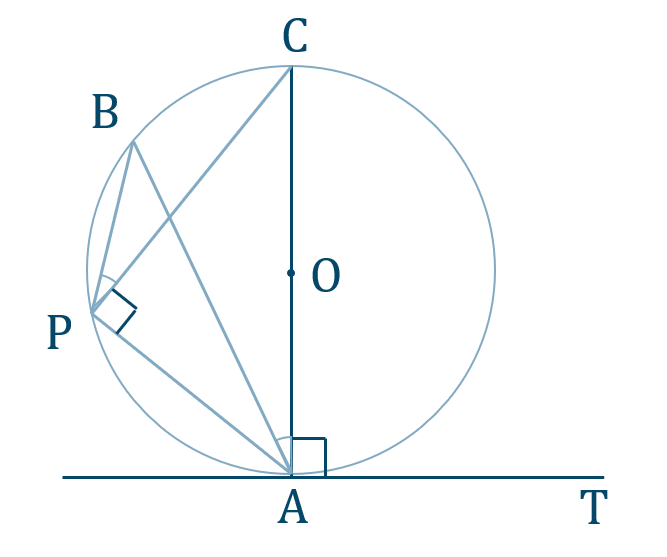
鈍角の場合
直径 \({\rm AC}\) を引くと、
\(\angle{\rm APC}=\angle{\rm TAC}=90^\circ\)
これより、
\(\angle{\rm BAT}=\angle{\rm BAC}+90^\circ\)
\(\angle{\rm APB}=90^\circ+\angle{\rm BPC}\)
また、弧 \({\rm BC}\) に対する円周角の定理より、
\(\angle{\rm BAC}=\angle{\rm BPC}\)
したがって、
\(\angle{\rm BAT}=\angle{\rm APB}\)
[終]
p.86
練習22
[証明]方べきの定理より、
\({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\)
ここで、\({\rm PC}=r+{\rm PO},{\rm PF}=r-{\rm PO}\) であることより、
\({\rm PA}\cdot{\rm PB}=(r+{\rm PO})(r-{\rm PO})\)
したがって、
\({\rm PA}\cdot{\rm PB}=r^2-{\rm PO}^2\) [終]
練習22
[証明]方べきの定理より、
\({\rm PA}\cdot{\rm PB}={\rm PC}\cdot{\rm PD}\)
ここで、\({\rm PC}=r+{\rm PO},{\rm PF}=r-{\rm PO}\) であることより、
\({\rm PA}\cdot{\rm PB}=(r+{\rm PO})(r-{\rm PO})\)
したがって、
\({\rm PA}\cdot{\rm PB}=r^2-{\rm PO}^2\) [終]
p.87
練習23
\(x=2\sqrt{6}\)
練習23
\(x=2\sqrt{6}\)
p.89
練習25
\(60^\circ\)
練習25
\(60^\circ\)
p.92
練習29
四角形 \(\rm ABCP\) は4つの辺が等しいのでひし形となる
したがって、直線 \(\rm PC\) は直線 \(l\) と平行となる
練習29
四角形 \(\rm ABCP\) は4つの辺が等しいのでひし形となる
したがって、直線 \(\rm PC\) は直線 \(l\) と平行となる
問題
p.95
1
[証明]

点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
\({\rm CB\parallel QR,CA\parallel PR,AB\parallel QP}\)
ここで、\({\rm CB\parallel QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
1
[証明]
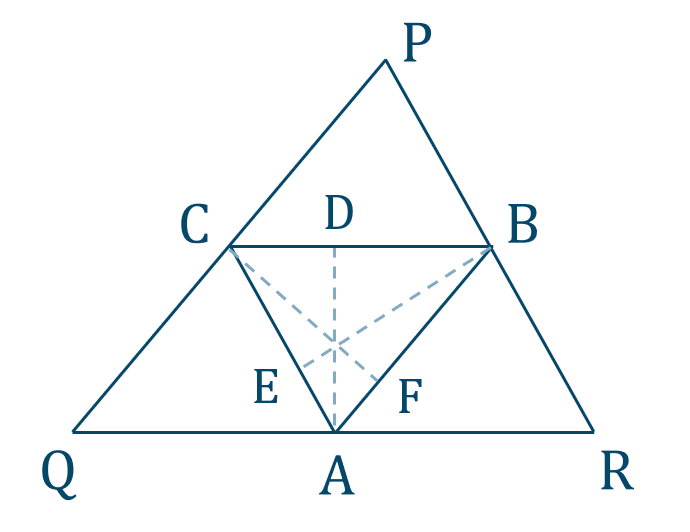
点 \({\rm A}\) から \({\rm BC}\) に下した垂線との交点を \({\rm D}\)
点 \({\rm B}\) から \({\rm AC}\) に下した垂線との交点を \({\rm E}\)
点 \({\rm C}\) から \({\rm AB}\) に下した垂線との交点を \({\rm F}\)
とする
中点連結定理より、
\({\rm CB\parallel QR,CA\parallel PR,AB\parallel QP}\)
ここで、\({\rm CB\parallel QR}\) かつ \({\rm AD\perp CB}\) より \({\rm AD\perp QR}\)
また、点 \({\rm A}\) は \({\rm QR}\) の中点であるので、 \({\rm AD}\) は辺 \({\rm QR}\) の垂直二等分線となる
同様に考えて、
\({\rm BE}\) は辺 \({\rm PR}\) の垂直二等分線となる
\({\rm CF}\) は辺 \({\rm QP}\) の垂直二等分線となる
したがって、\({\rm AD,BE,CF}\) は \(\triangle{\rm PQR}\) の外心で交わる[終]
p.95
2
[証明]

点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
2
[証明]
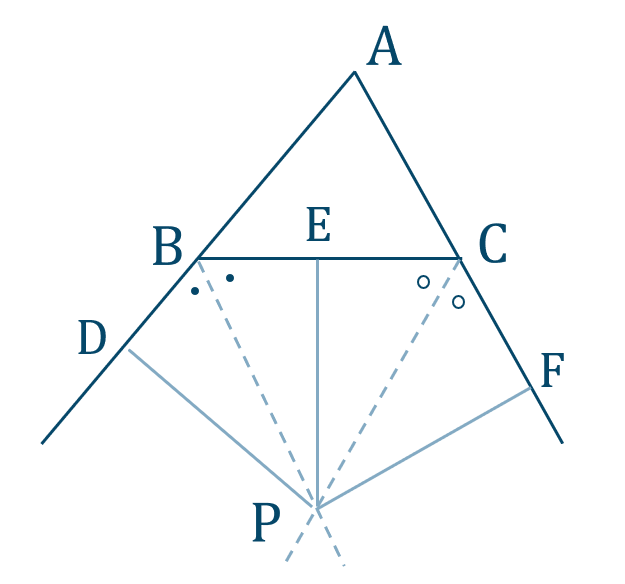
点 \({\rm P}\) から \({\rm AB}\) の延長線上に下した垂線を \({\rm PD}\)
点 \({\rm P}\) から \({\rm BC}\) に下した垂線を \({\rm PE}\)
点 \({\rm P}\) から \({\rm AC}\) の延長線上に下した垂線を \({\rm PF}\)
とする
\(\angle{\rm DBE}\) の二等分線が \({\rm BP}\) となるので \({\rm PD=PE}\)
\(\angle{\rm FCE}\) の二等分線が \({\rm CP}\) となるので \({\rm PF=PE}\)
よって、\({\rm PD=PF}\)
また、\({\rm AP}\) が共通の辺であるので、\(\triangle{\rm APD}\) と \(\triangle{\rm APF}\) は斜辺と他の1辺がそれぞれ等しいので、
\(\triangle{\rm APD}\sim\triangle{\rm APF}\)
対応する角が等しいので、
\(\angle{\rm DAP}=\angle{\rm FAP}\)
よって、点 \({\rm P}\) は \(\angle{\rm A}\) の二等分線上にある[終]
p.95
3
\({\small (1)}~\)
[証明] \(\triangle {\rm ABC}\) において、チェバの定理より、$$~~~{\rm \frac{AE}{EB}\cdot\frac{BD}{DC}\cdot\frac{CF}{FA}}=1$$ここで、\({\rm AE:EB}=1:1~,~{\rm AF:FC}=1:1\) より、$$~~~ \frac{1}{1}\cdot {\rm \frac{BD}{DC}}\cdot\frac{1}{1}=1$$よって、$$~~~{\rm \frac{BD}{DC}}=1$$これより、
\({\rm BD:DC}=1:1\)
したがって、点 \({\rm D}\) は線分 \({\rm BC}\) の中点となるので、三角形の3本の中線は1点で交わる [終]
\({\small (2)}~\)
[証明] \(\triangle {\rm ABD}\) において、メネラウスの定理より、$$~~~{\rm \frac{AE}{EB}\cdot\frac{BC}{CD}\cdot\frac{DG}{GA}}=1$$ここで、\({\rm AE:EB}=1:1~,~{\rm BC:CD}=2:1\) より、$$~~~ \frac{1}{1}\cdot\frac{2}{1}\cdot {\rm \frac{DG}{GA}}=1$$よって、$$~~~{\rm \frac{DG}{GA}}=\frac{1}{2}$$これより、
\({\rm AG:GD}=2:1\) [終]
3
\({\small (1)}~\)
[証明] \(\triangle {\rm ABC}\) において、チェバの定理より、$$~~~{\rm \frac{AE}{EB}\cdot\frac{BD}{DC}\cdot\frac{CF}{FA}}=1$$ここで、\({\rm AE:EB}=1:1~,~{\rm AF:FC}=1:1\) より、$$~~~ \frac{1}{1}\cdot {\rm \frac{BD}{DC}}\cdot\frac{1}{1}=1$$よって、$$~~~{\rm \frac{BD}{DC}}=1$$これより、
\({\rm BD:DC}=1:1\)
したがって、点 \({\rm D}\) は線分 \({\rm BC}\) の中点となるので、三角形の3本の中線は1点で交わる [終]
\({\small (2)}~\)
[証明] \(\triangle {\rm ABD}\) において、メネラウスの定理より、$$~~~{\rm \frac{AE}{EB}\cdot\frac{BC}{CD}\cdot\frac{DG}{GA}}=1$$ここで、\({\rm AE:EB}=1:1~,~{\rm BC:CD}=2:1\) より、$$~~~ \frac{1}{1}\cdot\frac{2}{1}\cdot {\rm \frac{DG}{GA}}=1$$よって、$$~~~{\rm \frac{DG}{GA}}=\frac{1}{2}$$これより、
\({\rm AG:GD}=2:1\) [終]
p.95
4
\({\small (1)}~39^\circ\) \({\small (2)}~32^\circ\)
4
\({\small (1)}~39^\circ\) \({\small (2)}~32^\circ\)
p.96
5
[証明] 図のように、線分 \({\rm BD}\) を延ばした点を \({\rm E}\) とする

四角形 \({\rm ACQD}\) は円に内接するので、内角は対角の外角と等しいのとより、
\(\angle{\rm ACQ}=\angle{\rm BPQ}\)
また、四角形 \({\rm PQDB}\) は円に内接するので、内角は対角の外角と等しいのとより、
\(\angle{\rm BPQ}=\angle{\rm EDQ}\)
よって、
\(\angle{\rm ACQ}=\angle{\rm EDQ}\)
したがって、錯角が等しくなるので、
\({\rm AC\parallel BD}\) [終]
5
[証明] 図のように、線分 \({\rm BD}\) を延ばした点を \({\rm E}\) とする
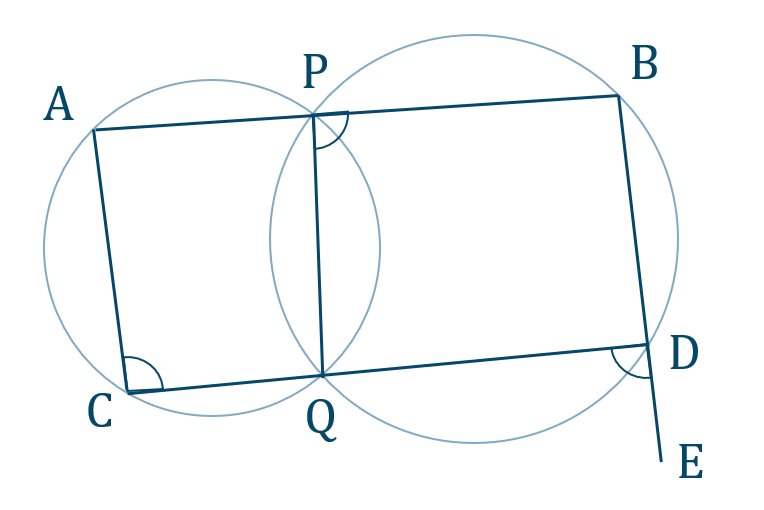
四角形 \({\rm ACQD}\) は円に内接するので、内角は対角の外角と等しいのとより、
\(\angle{\rm ACQ}=\angle{\rm BPQ}\)
また、四角形 \({\rm PQDB}\) は円に内接するので、内角は対角の外角と等しいのとより、
\(\angle{\rm BPQ}=\angle{\rm EDQ}\)
よって、
\(\angle{\rm ACQ}=\angle{\rm EDQ}\)
したがって、錯角が等しくなるので、
\({\rm AC\parallel BD}\) [終]
p.96
6
[証明] 図のように、点 \({\rm P}\) における共通接線を引き、この線上の点を \({\rm E~,~F}\) とする

\(\triangle {\rm ACP}\) の接弦定理より、
\(\angle{\rm ACP}=\angle{\rm APE}\)
\(\triangle {\rm BDP}\) の接弦定理より、
\(\angle{\rm BDP}=\angle{\rm BPF}\)
ここで、対頂角が等しいので、
\(\angle{\rm APE}=\angle{\rm BPF}\)
よって、
\(\angle{\rm ACP}=\angle{\rm BDP}\)
したがって、錯角が等しいので、
\({\rm AC\parallel DB}\) [終]
6
[証明] 図のように、点 \({\rm P}\) における共通接線を引き、この線上の点を \({\rm E~,~F}\) とする
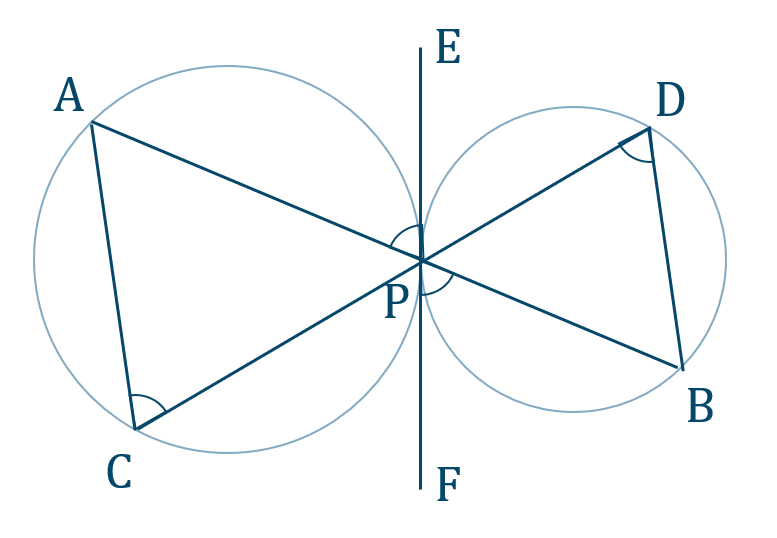
\(\triangle {\rm ACP}\) の接弦定理より、
\(\angle{\rm ACP}=\angle{\rm APE}\)
\(\triangle {\rm BDP}\) の接弦定理より、
\(\angle{\rm BDP}=\angle{\rm BPF}\)
ここで、対頂角が等しいので、
\(\angle{\rm APE}=\angle{\rm BPF}\)
よって、
\(\angle{\rm ACP}=\angle{\rm BDP}\)
したがって、錯角が等しいので、
\({\rm AC\parallel DB}\) [終]
p.96
7

7
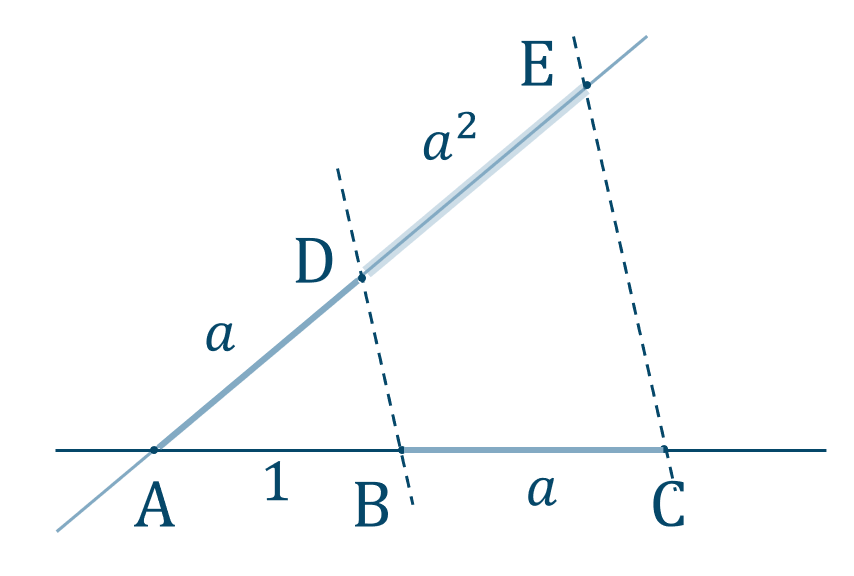
p.96
8
ア:\(4\) イ:\(3\) ウ:\(2\) エ:\(0\) オ:\(7\)
カ:\(7\) キ:\(5\) ク:\(3\) ケ:\(0\) コ:\(0\)
8
ア:\(4\) イ:\(3\) ウ:\(2\) エ:\(0\) オ:\(7\)
カ:\(7\) キ:\(5\) ク:\(3\) ケ:\(0\) コ:\(0\)
第2節 空間図形
p.99
練習34
[証明] 条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である
また(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
練習34
[証明] 条件より、\({\rm AO\perp}\) 平面 \({\rm BCD}\) であるので、
\({\rm BC\perp AO}\)
また、
\({\rm OE\perp BC}\)
これより、\({\rm BC}\) は \({\rm AO}\) と \({\rm OE}\) の定める平面 \({\rm AEO}\) にも垂直である
また(1)より、\({\rm BC\perp}\) 平面 \({\rm AEO}\)
直線 \({\rm AE}\) は平面 \({\rm AEO}\) 上にあるので、
\({\rm AE\perp BC}\) [終]
p.100
練習35
\({\small (1)}~\)

図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \parallel \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
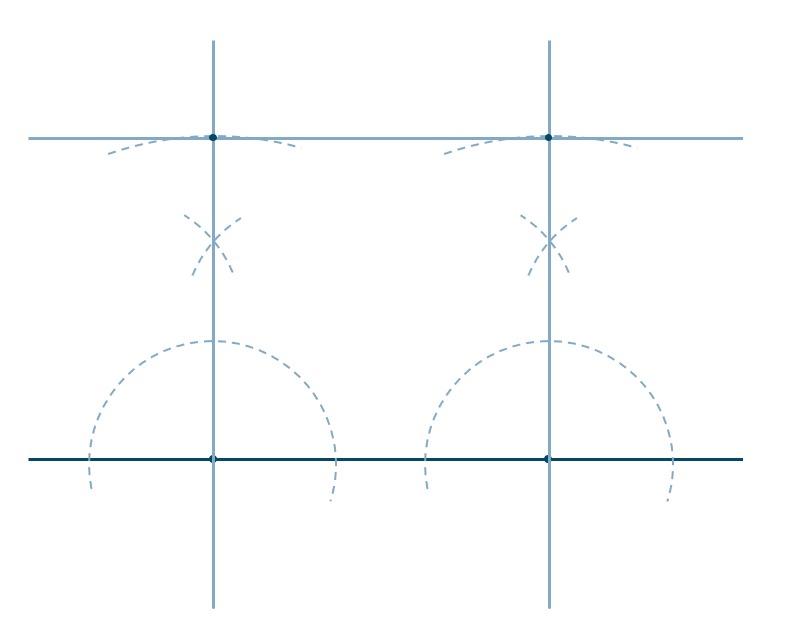
\({\small (3)}~\)

図より、\({\rm \alpha \parallel l , \beta \parallel l}\) としても \({\rm \alpha \parallel \beta}\) でない
よって、正しくない
練習35
\({\small (1)}~\)
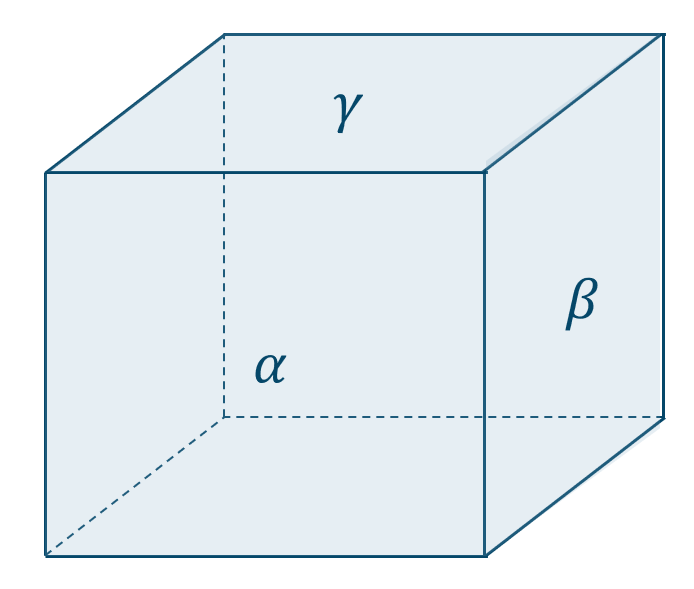
図より、\({\rm \alpha \perp \beta , \beta \perp \gamma}\) としても \({\rm \alpha \parallel \gamma}\) でない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)
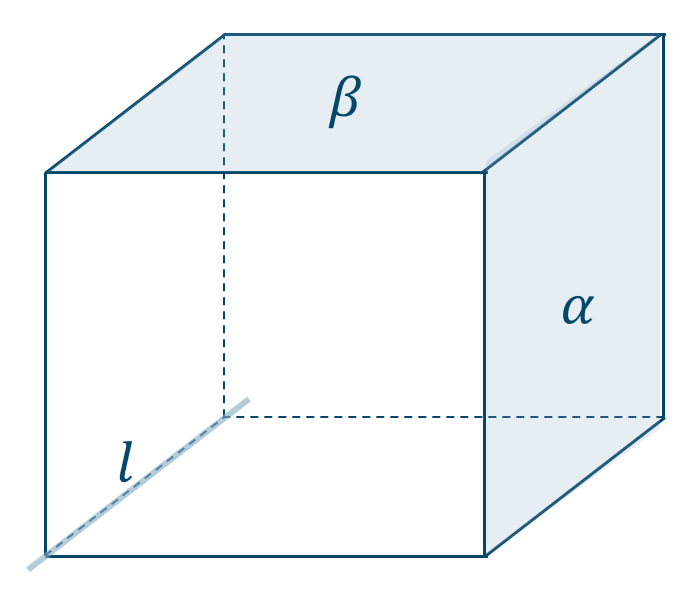
図より、\({\rm \alpha \parallel l , \beta \parallel l}\) としても \({\rm \alpha \parallel \beta}\) でない
よって、正しくない
p.101
研究1
\({\small (1)}~\)[証明]
\(\rm EA \perp \) 面 \(\rm EFGH\)
\(\rm EK \perp FH\)
よって、三垂線の定理1より
\(\rm AK \perp FH\) [終]
\({\small (2)}~\)[証明] \(\rm AE \perp \) 面 \(\rm ABCD\) より、
\(\rm BD \perp AE\)
正方形 \(\rm ABCD\) の対角線は直交するので、
\(\rm BD \perp AC\)
これらより、\(\rm BD \perp \) 面 \(\rm ACE\) となり、点 \(\rm G\) が面 \(\rm ACE\) 上にあるので、
\(\rm AG \perp BD\) [終]
研究1
\({\small (1)}~\)[証明]
\(\rm EA \perp \) 面 \(\rm EFGH\)
\(\rm EK \perp FH\)
よって、三垂線の定理1より
\(\rm AK \perp FH\) [終]
\({\small (2)}~\)[証明] \(\rm AE \perp \) 面 \(\rm ABCD\) より、
\(\rm BD \perp AE\)
正方形 \(\rm ABCD\) の対角線は直交するので、
\(\rm BD \perp AC\)
これらより、\(\rm BD \perp \) 面 \(\rm ACE\) となり、点 \(\rm G\) が面 \(\rm ACE\) 上にあるので、
\(\rm AG \perp BD\) [終]
p.103
練習36
正四面体 \(4\) 正三角形 \(4\) \(6\)
正六面体 \(6\) 正方形 \(8\) \(12\)
正十二面体 \(12\) 正五角形 \(20\) \(30\)
正二十面体 \(20\) 正三角形 \(12\) \(30\)
練習36
正四面体 \(4\) 正三角形 \(4\) \(6\)
正六面体 \(6\) 正方形 \(8\) \(12\)
正十二面体 \(12\) 正五角形 \(20\) \(30\)
正二十面体 \(20\) 正三角形 \(12\) \(30\)
p.103
練習37
それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
練習37
それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
p.103
練習38
\({\small (1)}~\)面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\({\small (2)}~v-e+f=14-24+12=2\)
練習38
\({\small (1)}~\)面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\({\small (2)}~v-e+f=14-24+12=2\)
p.104
練習39
[証明] \({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である [終]
練習39
[証明] \({\rm P,Q,R,S,T,U}\) は各辺の中点である
中点連結定理より、立体 \({\rm PQRSTU}\) の各辺はもとの正四面体 \({\rm ABCD}\) の辺の長さの半分となる
よって、立体 \({\rm PQRSTU}\) の各面はすべて合同な正三角形となる
また、この立体 \({\rm PQRSTU}\) の各頂点に集まる正三角形はすべて \(4\) となり等しい
したがって、立体 \({\rm PQRSTU}\) は正八面体である [終]
p.105
研究1
\({\Large \frac{\sqrt{2}}{12}}a^3\)
研究1
\({\Large \frac{\sqrt{2}}{12}}a^3\)
問題
p.107
9
\({\small (1)}~\)

図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
9
\({\small (1)}~\)
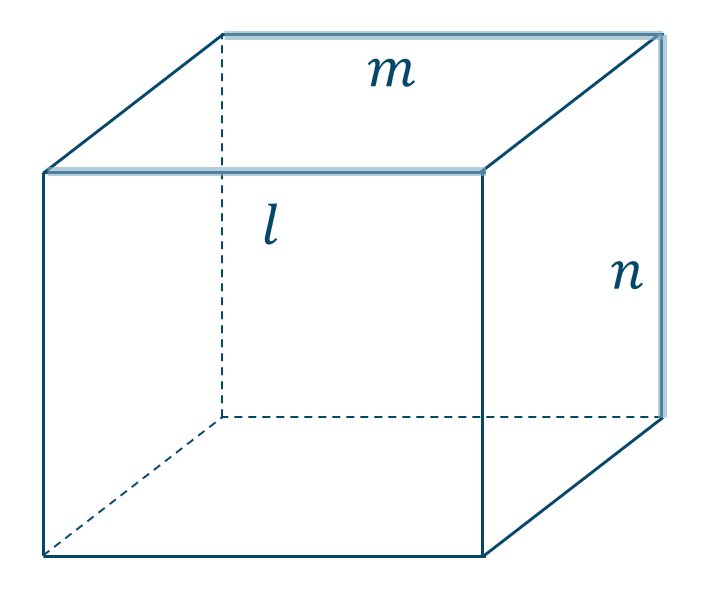
図より、\(l \parallel m\) で \(m\) と \(n\) は交わるが、\(l\) と \(n\) はねじれの位置にあり交わらない
よって、正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しい
p.107
10
\({\small (1)}~\)
[証明] \({\rm OA\perp OB~,~OA\perp OC}\) より、
\({\rm OA}\perp\triangle {\rm OBC}\)
よって、\({\rm BC}\) は \(\triangle {\rm OBC}\) 上の辺であるので、
\({\rm OA\perp BC}\) [終]
[証明] \({\rm OH}\perp\triangle {\rm ABC}\) より、辺 \({\rm BC}\) は \(\triangle {\rm ABC}\) の辺より、
\({\rm OH\perp BC}\) [終]
\({\small (2)}~\)
[証明] (1) より、
\({\rm OA\perp BC~,~OH\perp BC}\)
これより、
\({\rm BC}\perp\triangle {\rm OAH}\)
ここで、辺 \({\rm AH}\) は \(\triangle {\rm OAH}\) 上の辺であるので、
\({\rm AH\perp BC}\) [終]
10
\({\small (1)}~\)
[証明] \({\rm OA\perp OB~,~OA\perp OC}\) より、
\({\rm OA}\perp\triangle {\rm OBC}\)
よって、\({\rm BC}\) は \(\triangle {\rm OBC}\) 上の辺であるので、
\({\rm OA\perp BC}\) [終]
[証明] \({\rm OH}\perp\triangle {\rm ABC}\) より、辺 \({\rm BC}\) は \(\triangle {\rm ABC}\) の辺より、
\({\rm OH\perp BC}\) [終]
\({\small (2)}~\)
[証明] (1) より、
\({\rm OA\perp BC~,~OH\perp BC}\)
これより、
\({\rm BC}\perp\triangle {\rm OAH}\)
ここで、辺 \({\rm AH}\) は \(\triangle {\rm OAH}\) 上の辺であるので、
\({\rm AH\perp BC}\) [終]
p.107
11
\(12+4\sqrt{3}~,~{\large \frac{20}{3}}\)
11
\(12+4\sqrt{3}~,~{\large \frac{20}{3}}\)
p.107
12
ア:\(3\) イ:\(6\) ウ:\(0\) エ:\(9\) オ:\(0\)
12
ア:\(3\) イ:\(6\) ウ:\(0\) エ:\(9\) オ:\(0\)
章末問題 図形の性質
章末問題A
p.108
1
[証明]

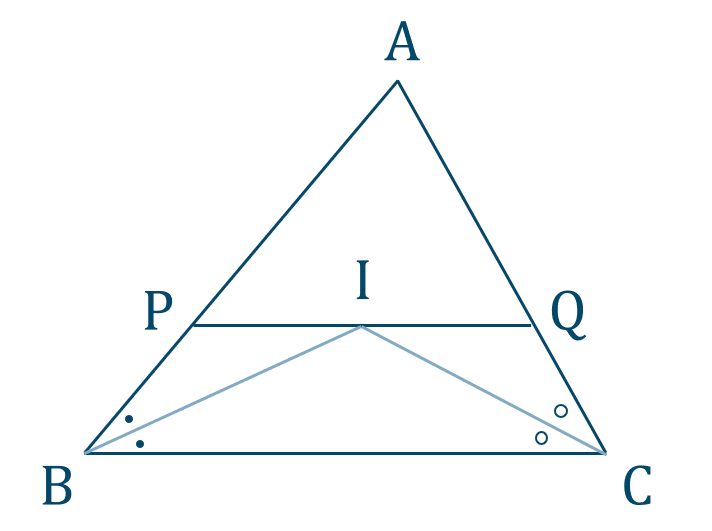
点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
1
[証明]
点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm PBI}=\angle{\rm IBC}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm PIB}=\angle{\rm IBC}\)
よって、\(\angle{\rm PBI}=\angle{\rm PIB}\) となり \(\triangle{\rm PBI}\) は \({\rm PB=PI}\) の二等辺三角形となる
同様に、点 \(\rm I\) は \(\triangle{\rm ABC}\) の内心であるので、
\(\angle{\rm QCI}=\angle{\rm ICB}\)
また、\({\rm PQ \parallel BC}\) の錯角より、
\(\angle{\rm QIC}=\angle{\rm ICB}\)
よって、\(\angle{\rm QCI}=\angle{\rm QIC}\) となり \(\triangle{\rm QIC}\) は \({\rm QI=QC}\) の二等辺三角形となる
したがって、\(\rm PQ=PI+IQ\) であるので、
\(\rm PQ=PB+QC\) [終]
p.108
2
\({\small (1)}~125^{\circ}\) \({\small (2)}~52^{\circ}\)
2
\({\small (1)}~125^{\circ}\) \({\small (2)}~52^{\circ}\)
p.108
3
\({\small (1)}~45^{\circ}\) \({\small (2)}~2\)
3
\({\small (1)}~45^{\circ}\) \({\small (2)}~2\)
p.108
4
[証明] 円\({\rm O}\) についての方べきの定理より、
\({\rm EA\cdot EB=EC}^2\) …①
また、円 \({\rm O’}\) についての方べきの定理より、
\({\rm EA\cdot EB=ED}^2\)
よって、
\({\rm EC=ED}\) …②
次に、\({\rm A~,~C~,~D~,~F}\) を通る円についての方べきの定理より、
\({\rm EA\cdot EF=EC\cdot ED}\)
②より、
\({\rm EA\cdot EF=EC}^2\)
①より、
\({\rm EA\cdot EF=EA\cdot EB}\)
よって、
\({\rm EF=EB}\) …③
したがって、②と③より、対角線のそれぞれの中点が等しいので、四角形 \({\rm BDFC}\) は平行四辺形である [終]
4
[証明] 円\({\rm O}\) についての方べきの定理より、
\({\rm EA\cdot EB=EC}^2\) …①
また、円 \({\rm O’}\) についての方べきの定理より、
\({\rm EA\cdot EB=ED}^2\)
よって、
\({\rm EC=ED}\) …②
次に、\({\rm A~,~C~,~D~,~F}\) を通る円についての方べきの定理より、
\({\rm EA\cdot EF=EC\cdot ED}\)
②より、
\({\rm EA\cdot EF=EC}^2\)
①より、
\({\rm EA\cdot EF=EA\cdot EB}\)
よって、
\({\rm EF=EB}\) …③
したがって、②と③より、対角線のそれぞれの中点が等しいので、四角形 \({\rm BDFC}\) は平行四辺形である [終]
p.108
5
[証明]

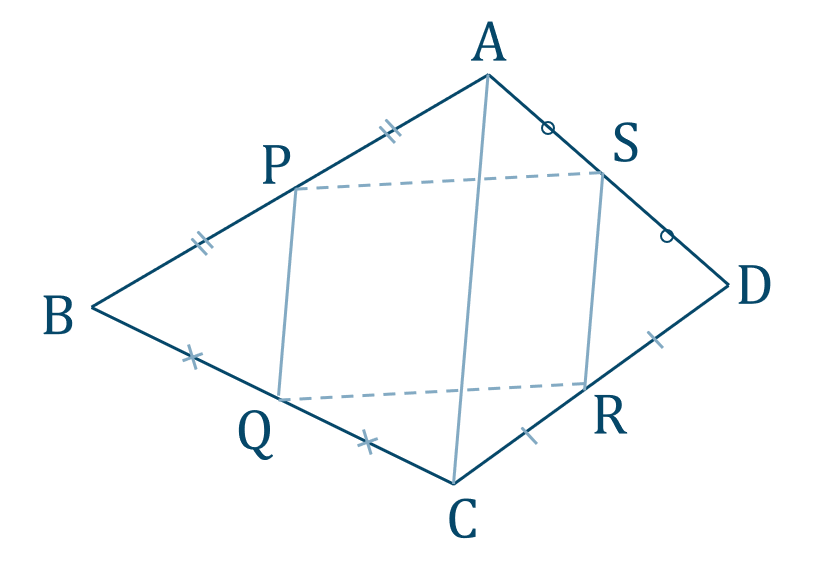
\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \parallel AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \parallel AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \parallel SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる
5
[証明]
\(\triangle{\rm BAC}\) において、点 \(\rm P,Q\) が中点であるので、中点連結定理より、
\({\rm PQ \parallel AC,PQ={\large \frac{1}{2}}AC}\)
\(\triangle{\rm DAC}\) において、点 \(\rm S,R\) が中点であるので、中点連結定理より、
\({\rm SR \parallel AC,SR={\large \frac{1}{2}}AC}\)
よって、\({\rm PQ \parallel SR,PQ=SR}\)
1組の対辺が平行で長さが等しいので、四角形 \({\rm PQRS}\) は平行四辺形となる
章末問題B
p.109
6
[証明]

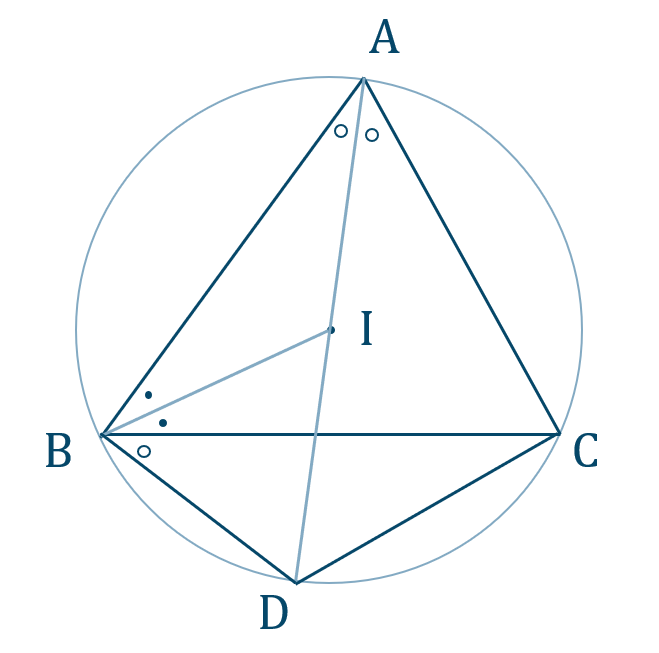
図より、内心 \({\rm I}\) は角の二等分線の交点より、
\(\angle{\rm BAD}=\angle{\rm CAD}=x\)
円周角が等しいことより、対応する弦の長さも等しくなるので、
\({\rm DB=DC}\) …①
次に、内心 \({\rm I}\) は角の二等分線の交点より、
\(\angle{\rm ABI}=\angle{\rm CIB}=y\)
また、弧 \({\rm DC}\) よ円周角より、
\(\angle{\rm DBC}=\angle{\rm DAC}=x\)
ここで、
\(\angle{\rm IBD}=x+y\)
また、\(\triangle {\rm AIB}\) の外角は他の内角の和より、
\(\angle{\rm BID}=x+y\)
よって、\(\triangle {\rm DBI}\) は二等辺三角形となり
\({\rm DB=DI}\) …②
したがって、①と②より、
\({\rm DB=DC=DI}\) [終]
6
[証明]
図より、内心 \({\rm I}\) は角の二等分線の交点より、
\(\angle{\rm BAD}=\angle{\rm CAD}=x\)
円周角が等しいことより、対応する弦の長さも等しくなるので、
\({\rm DB=DC}\) …①
次に、内心 \({\rm I}\) は角の二等分線の交点より、
\(\angle{\rm ABI}=\angle{\rm CIB}=y\)
また、弧 \({\rm DC}\) よ円周角より、
\(\angle{\rm DBC}=\angle{\rm DAC}=x\)
ここで、
\(\angle{\rm IBD}=x+y\)
また、\(\triangle {\rm AIB}\) の外角は他の内角の和より、
\(\angle{\rm BID}=x+y\)
よって、\(\triangle {\rm DBI}\) は二等辺三角形となり
\({\rm DB=DI}\) …②
したがって、①と②より、
\({\rm DB=DC=DI}\) [終]
p.109
7
[証明]

対角の和が \(180^\circ\) より、四角形 \({\rm AFDE}\) は円に内接する
よって、円周角の定理より、
\(\angle{\rm AEF}=\angle{\rm APF}\)
次に、対角の和が \(180^\circ\) より、四角形 \({\rm FBDP}\) は円に内接する
よって、内角と対角の外角は等しいので、
\(\angle{\rm FBD}=\angle{\rm APF}\)
これらより、
\(\angle{\rm FBD}=\angle{\rm AEF}\)
したがって、四角形 \({\rm BCEF}\) は内角と対角の外角が等しいくなるので円に内接する [終]
7
[証明]
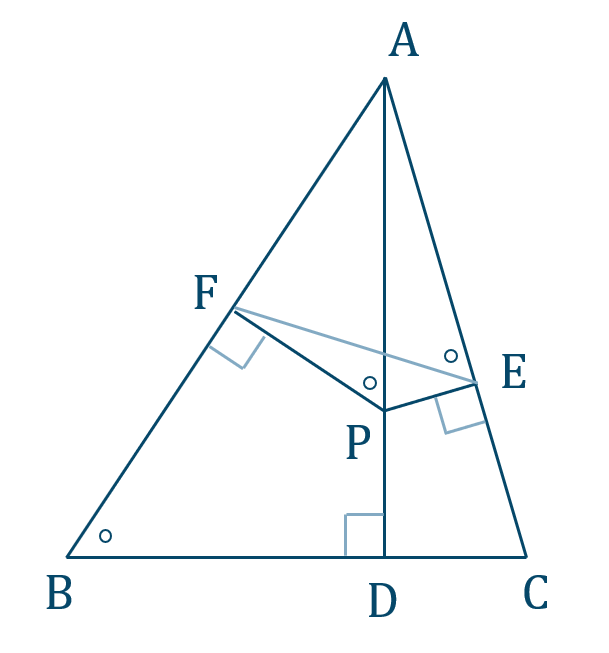
対角の和が \(180^\circ\) より、四角形 \({\rm AFDE}\) は円に内接する
よって、円周角の定理より、
\(\angle{\rm AEF}=\angle{\rm APF}\)
次に、対角の和が \(180^\circ\) より、四角形 \({\rm FBDP}\) は円に内接する
よって、内角と対角の外角は等しいので、
\(\angle{\rm FBD}=\angle{\rm APF}\)
これらより、
\(\angle{\rm FBD}=\angle{\rm AEF}\)
したがって、四角形 \({\rm BCEF}\) は内角と対角の外角が等しいくなるので円に内接する [終]
p.109
8
\({\small (1)}~\)
[証明] 仮定より、
\(\angle{\rm BAE}=\angle{\rm DAC}\)
また、弧 \({\rm AD}\) における円周角の定理より、
\(\angle{\rm AEF}=\angle{\rm ACD}\)
よって、2つの角がそれぞれ等しいので、
\(\triangle {\rm ABE} \sim \triangle {\rm ADC}\) [終]
\({\small (2)}~\)
[証明] (1) より、
\({\rm AB:AE=AD:AC}\)
よって、
\({\rm AB\cdot AC=AE\cdot AD}\)
ここで、\({\rm AE=AD+DE}\) より、
\({\rm AB\cdot AC=(AD+DE)\cdot AD}\)
ゆえに、
\({\rm AB\cdot AC=AD}^2+{\rm DE\cdot AD}\) …①
次に、方べきの定理より、
\({\rm AD\cdot DE=BD\cdot CD}\)
①に代入すると、
\({\rm AB\cdot AC=AD}^2+{\rm BD\cdot CD}\)
したがって、
\({\rm AD}^2={\rm AB\cdot AC-BD\cdot CD}\) [終]
8
\({\small (1)}~\)
[証明] 仮定より、
\(\angle{\rm BAE}=\angle{\rm DAC}\)
また、弧 \({\rm AD}\) における円周角の定理より、
\(\angle{\rm AEF}=\angle{\rm ACD}\)
よって、2つの角がそれぞれ等しいので、
\(\triangle {\rm ABE} \sim \triangle {\rm ADC}\) [終]
\({\small (2)}~\)
[証明] (1) より、
\({\rm AB:AE=AD:AC}\)
よって、
\({\rm AB\cdot AC=AE\cdot AD}\)
ここで、\({\rm AE=AD+DE}\) より、
\({\rm AB\cdot AC=(AD+DE)\cdot AD}\)
ゆえに、
\({\rm AB\cdot AC=AD}^2+{\rm DE\cdot AD}\) …①
次に、方べきの定理より、
\({\rm AD\cdot DE=BD\cdot CD}\)
①に代入すると、
\({\rm AB\cdot AC=AD}^2+{\rm BD\cdot CD}\)
したがって、
\({\rm AD}^2={\rm AB\cdot AC-BD\cdot CD}\) [終]
p.109
9
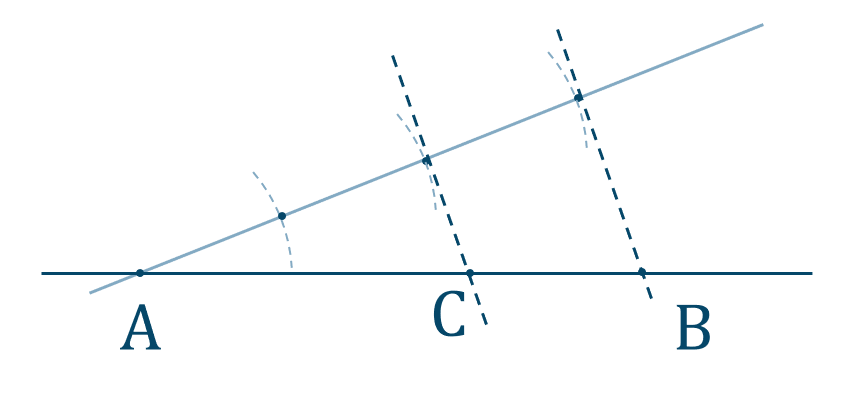
\({\small (1)}~\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、

これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
9
\({\small (1)}~\)
[証明] \(\rm AC\) の中点を \(\rm E\) とすると、
\(\triangle{\rm ABC}\) の重心が \(\rm P\) であるので、
\({\rm BP:PE}=2:1\)
また、\(\triangle{\rm ACD}\) の重心が \(\rm Q\) であるので、
\({\rm DQ:QE}=2:1\)
\(\triangle{\rm ABC}\) を図で表すと、
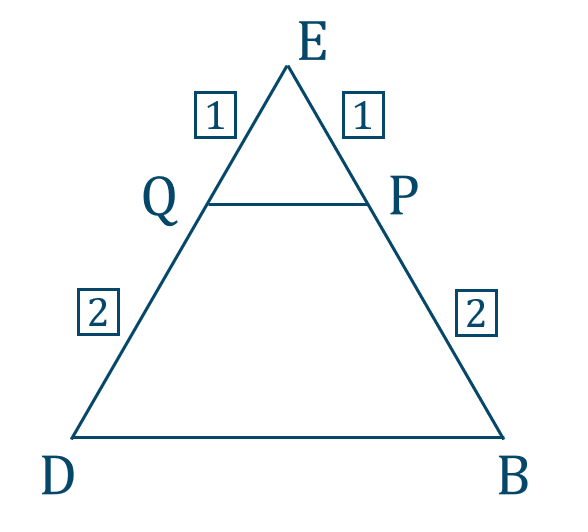
これより、平行線と比の関係より、
\({\rm PQ}={\large \frac{1}{3}}{\rm BD}\)
同様に考えて、多面体 \(\rm PQRS\) のすべての辺は、もとの正四面体 \(\rm ABCD\) の長さの \(\frac{1}{3}\) となる
また、多面体 \(\rm PQRS\) の4つの頂点に集める正三角形は数はすべて3で等しい
したがって、多面体 \(\rm PQRS\) は正四面体である[終]
\({\small (2)}~1:27\)
次のページ「第3章 整数の性質」