文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
1章 数と式
3章 2次関数
4章 図形と計量
5章 データの分析
2章 集合と論証
1節 集合
p.50
問1
\(5\in {\rm A}~,~6\notin {\rm A}\)
問1
\(5\in {\rm A}~,~6\notin {\rm A}\)
p.51
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{-2,2\}\)
\({\small (3)}~\{5,10,15,20\cdots\}\)
→ 集合の表し方と要素
問2
\({\small (1)}~\{2,3,5,7\}\)
\({\small (2)}~\{-2,2\}\)
\({\small (3)}~\{5,10,15,20\cdots\}\)
→ 集合の表し方と要素
p.51
問3
\({\rm A}\)、\({\rm C}\)
問3
\({\rm A}\)、\({\rm C}\)
p.52
問4
\({\small (1)}~\)
\({\rm A\cap B}=\{1,3,5\}\)
\({\rm A\cup B}=\{1,2,3,4,5,6,7\}\)
\({\small (2)}~\)
\({\rm A\cap B}=\{1,2,4,8\}\)
\({\rm A\cup B}=\{1,2,3,4,6,8,12,16,24,32\}\)
\({\small (3)}~\)
\({\rm A\cap B}=\{3\}\)
\({\rm A\cup B}=\{1,3,4,5,7,9\}\)
→ 共通部分と和集合
問4
\({\small (1)}~\)
\({\rm A\cap B}=\{1,3,5\}\)
\({\rm A\cup B}=\{1,2,3,4,5,6,7\}\)
\({\small (2)}~\)
\({\rm A\cap B}=\{1,2,4,8\}\)
\({\rm A\cup B}=\{1,2,3,4,6,8,12,16,24,32\}\)
\({\small (3)}~\)
\({\rm A\cap B}=\{3\}\)
\({\rm A\cup B}=\{1,3,4,5,7,9\}\)
→ 共通部分と和集合
p.53
問5
\({\small (1)}~\phi~,~\{3\}~,~\{4\}~,~\{3,4\}\)
\({\small (2)}~\phi~,~\{5\}~,~\{6\}~,~\{7\}\)
\(\{5,6\}~,~\{6,7\}~,~\{5,7\}~,~\{5,6,7\}\)
→ 集合の包含関係と部分集合
問5
\({\small (1)}~\phi~,~\{3\}~,~\{4\}~,~\{3,4\}\)
\({\small (2)}~\phi~,~\{5\}~,~\{6\}~,~\{7\}\)
\(\{5,6\}~,~\{6,7\}~,~\{5,7\}~,~\{5,6,7\}\)
→ 集合の包含関係と部分集合
p.53
問6
\({\small (1)}~{\rm \overline {A}}=\{1,3,5,7,8,9\}\)
\({\small (2)}~{\rm \overline {B}}=\{2,5,6,8,9\}\)
\({\small (3)}~{\rm \overline {A}\cap \overline {B}}=\{5,8,9\}\)
\({\small (4)}~{\rm \overline {A\cup B}}=\{5,8,9\}\)
問6
\({\small (1)}~{\rm \overline {A}}=\{1,3,5,7,8,9\}\)
\({\small (2)}~{\rm \overline {B}}=\{2,5,6,8,9\}\)
\({\small (3)}~{\rm \overline {A}\cap \overline {B}}=\{5,8,9\}\)
\({\small (4)}~{\rm \overline {A\cup B}}=\{5,8,9\}\)
p.54
問7
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、

この2つの和集合となるので、

これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
→ 補集合とド・モルガンの法則
問7
全体集合 \(\rm U\) とその部分集合 \({\rm A}~,~{\rm B}\) において、
\( \overline {{\rm A}} \cup \overline {{\rm B}} \) をベン図で表すと、
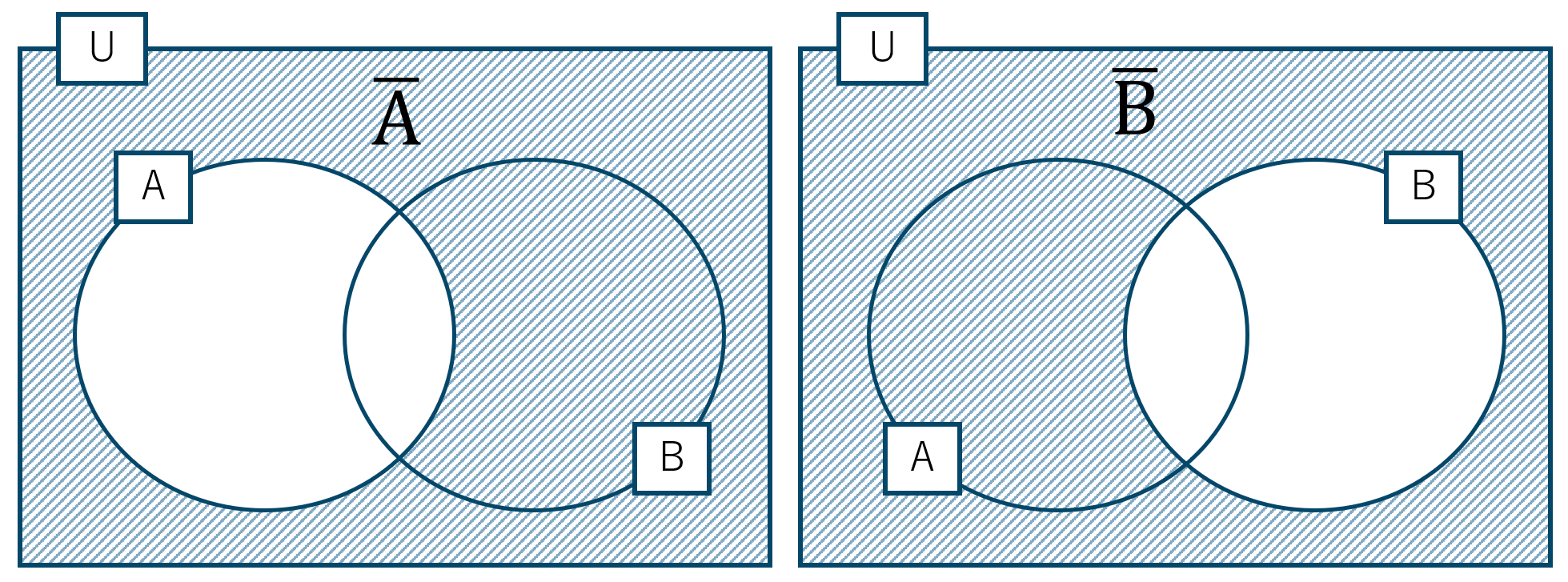
この2つの和集合となるので、
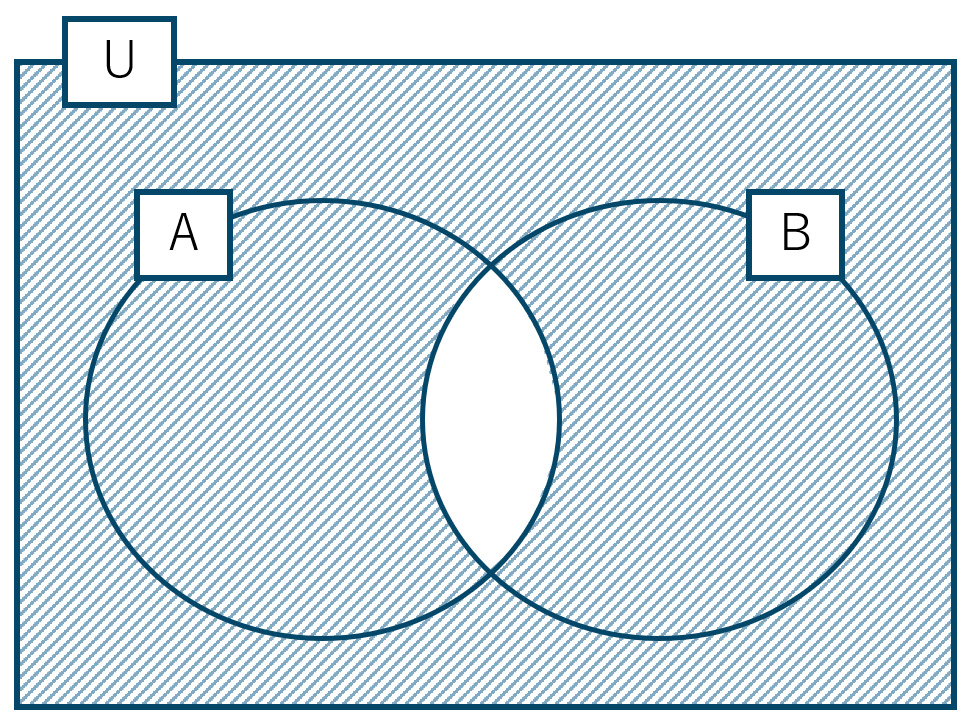
これは集合 \( {\rm A}\cap {\rm B} \) の補集合となるので、
\(\overline {{\rm A} \cap {\rm B}}=\overline {{\rm A}} \cup \overline {{\rm B}}\)
→ 補集合とド・モルガンの法則
Training
p.55
1
\({\small (1)}~{\rm A}\cap{\rm B}=\{x~|~5<x≦7\}\)
\({\small (2)}~{\rm A}\cup{\rm B}=\{x~|~3≦x<10\}\)
\({\small (3)}~{\rm \overline {A}}\cap{\rm \overline {B}}=\{x~|~x≦5~,~7<x\}\)
\({\small (4)}~{\rm \overline {A}}\cup{\rm \overline {B}}=\{x~|~x<3~,~10≦x\}\)
→ 数直線と集合
1
\({\small (1)}~{\rm A}\cap{\rm B}=\{x~|~5<x≦7\}\)
\({\small (2)}~{\rm A}\cup{\rm B}=\{x~|~3≦x<10\}\)
\({\small (3)}~{\rm \overline {A}}\cap{\rm \overline {B}}=\{x~|~x≦5~,~7<x\}\)
\({\small (4)}~{\rm \overline {A}}\cup{\rm \overline {B}}=\{x~|~x<3~,~10≦x\}\)
→ 数直線と集合
p.55
2
\({\small (1)}~{\rm B}=\{2,4,6,7,8,9\}\)
\({\small (2)}~{\rm A}\cap{\rm \overline {B}}=\{1,3\}\)
\({\small (3)}~{\rm A \cup \overline {B}}=\{1,3,4,5,6,8,10\}\)
\({\small (4)}~{\rm \overline {\overline {A} \cap B}}=\{1,3,4,5,6,8,10\}\)
2
\({\small (1)}~{\rm B}=\{2,4,6,7,8,9\}\)
\({\small (2)}~{\rm A}\cap{\rm \overline {B}}=\{1,3\}\)
\({\small (3)}~{\rm A \cup \overline {B}}=\{1,3,4,5,6,8,10\}\)
\({\small (4)}~{\rm \overline {\overline {A} \cap B}}=\{1,3,4,5,6,8,10\}\)
2節 命題と論証
p.56
問2
\(x=-1~,~3\)
問2
\(x=-1~,~3\)
p.56
問3
\(x>-4\)
問3
\(x>-4\)
p.58
問5
\(p:3~,~q:1\)
問5
\(p:3~,~q:1\)
p.58
問6
\({\small (1)}~\)真
\({\small (2)}~\)偽、反例 \(a=0~,~b=1\)
\({\small (3)}~\)偽、反例 \(n=2\)
→ 条件の真偽
問6
\({\small (1)}~\)真
\({\small (2)}~\)偽、反例 \(a=0~,~b=1\)
\({\small (3)}~\)偽、反例 \(n=2\)
→ 条件の真偽
p.59
問7
\({\small (1)}~\)十分 \({\small (2)}~\)必要
問7
\({\small (1)}~\)十分 \({\small (2)}~\)必要
p.59
問8
\({\small (1)}~\)十分条件である
\({\small (2)}~\)必要条件でも十分条件でもない
\({\small (3)}~\)必要十分条件
\({\small (4)}~\)必要条件である
→ 必要条件と十分条件
問8
\({\small (1)}~\)十分条件である
\({\small (2)}~\)必要条件でも十分条件でもない
\({\small (3)}~\)必要十分条件
\({\small (4)}~\)必要条件である
→ 必要条件と十分条件
p.60
問9
\({\small (1)}~\)自然数 \(n\) は偶数である
\({\small (2)}~x>-3\)
\({\small (3)}~x\) は \(5\) より小さい
問9
\({\small (1)}~\)自然数 \(n\) は偶数である
\({\small (2)}~x>-3\)
\({\small (3)}~x\) は \(5\) より小さい
p.61
問10
\({\small (1)}~\)

\(x<2\)
\({\small (2)}~\)

\(x<3\)
\({\small (3)}~\)

\(x≦5\)
問10
\({\small (1)}~\)
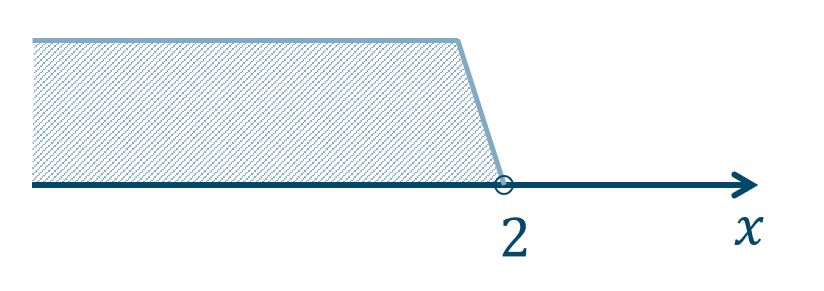
\(x<2\)
\({\small (2)}~\)

\(x<3\)
\({\small (3)}~\)

\(x≦5\)
p.62
問12
\({\small (1)}~\)
逆:\(x^2=0~\Rightarrow~x=0\)、真
裏:\(x\neq0~\Rightarrow~x^2\neq0\)、真
対偶:\(x^2\neq0~\Rightarrow~x\neq0\)、真
\({\small (2)}~\)
逆:自然数 \(n\) は \(12\) の約数
\(~\Rightarrow~\)自然数 \(n\) は \(6\) の約数、偽
裏:自然数 \(n\) は \(6\) の約数でない
\(~\Rightarrow~\)自然数 \(n\) は \(12\) の約数でない、偽
対偶:自然数 \(n\) は \(12\) の約数でない
\(~\Rightarrow~\)自然数 \(n\) は \(6\) の約数でない、真
\({\small (3)}~\)
逆:\(0<x<1\)
\(~\Rightarrow~-2<x<2\)、真
裏:\(x≦-2~,~2≦x\)
\(~\Rightarrow~x≦0~,~1≦x\)、真
対偶:\(x≦0~,~1≦x\)
\(~\Rightarrow~x≦-2~,~2≦x\)、偽
→ 逆と裏と対偶
問12
\({\small (1)}~\)
逆:\(x^2=0~\Rightarrow~x=0\)、真
裏:\(x\neq0~\Rightarrow~x^2\neq0\)、真
対偶:\(x^2\neq0~\Rightarrow~x\neq0\)、真
\({\small (2)}~\)
逆:自然数 \(n\) は \(12\) の約数
\(~\Rightarrow~\)自然数 \(n\) は \(6\) の約数、偽
裏:自然数 \(n\) は \(6\) の約数でない
\(~\Rightarrow~\)自然数 \(n\) は \(12\) の約数でない、偽
対偶:自然数 \(n\) は \(12\) の約数でない
\(~\Rightarrow~\)自然数 \(n\) は \(6\) の約数でない、真
\({\small (3)}~\)
逆:\(0<x<1\)
\(~\Rightarrow~-2<x<2\)、真
裏:\(x≦-2~,~2≦x\)
\(~\Rightarrow~x≦0~,~1≦x\)、真
対偶:\(x≦0~,~1≦x\)
\(~\Rightarrow~x≦-2~,~2≦x\)、偽
→ 逆と裏と対偶
p.63
問13
[証明]この命題の対偶は、
\(n\) が偶数ならば \(3n+5\) は奇数である
\(n\) が偶数より、整数 \(m\) を用いて \(n=2m\) とすると
\(3n+5=3\cdot2m+5\)
\(=6m+5=2(3m+2)+1\)
\(3m+2\) が整数より \(3n+5\) は奇数である
したがって、対偶が真より
もとの命題も真となる[終]
→ 対偶法
問13
[証明]この命題の対偶は、
\(n\) が偶数ならば \(3n+5\) は奇数である
\(n\) が偶数より、整数 \(m\) を用いて \(n=2m\) とすると
\(3n+5=3\cdot2m+5\)
\(=6m+5=2(3m+2)+1\)
\(3m+2\) が整数より \(3n+5\) は奇数である
したがって、対偶が真より
もとの命題も真となる[終]
→ 対偶法
p.64
問14
[証明]\(2\sqrt{2}+5\) が無理数でないと仮定すると
\(2\sqrt{2}+5\) は有理数となり、有理数 \(r\) で表すことができる
\(2\sqrt{2}+5=r\)
式変形すると、
\(\sqrt{2}={\Large \frac{r-5}{2}}\)
\(r\) が有理数であることより、\(\large \frac{r-5}{2}\) も有理数である
これより、この等式は \(\sqrt{2}\) が無理数であることに矛盾する
したがって、\(2\sqrt{2}+5\) が無理数である[終]
→ 背理法
問14
[証明]\(2\sqrt{2}+5\) が無理数でないと仮定すると
\(2\sqrt{2}+5\) は有理数となり、有理数 \(r\) で表すことができる
\(2\sqrt{2}+5=r\)
式変形すると、
\(\sqrt{2}={\Large \frac{r-5}{2}}\)
\(r\) が有理数であることより、\(\large \frac{r-5}{2}\) も有理数である
これより、この等式は \(\sqrt{2}\) が無理数であることに矛盾する
したがって、\(2\sqrt{2}+5\) が無理数である[終]
→ 背理法
Training
p.66
3
\({\small (1)}~\)真
\({\small (2)}~\)偽、反例 \(m=2~,~n=2\)
3
\({\small (1)}~\)真
\({\small (2)}~\)偽、反例 \(m=2~,~n=2\)
p.66
4
\({\small (1)}~\)必要条件でも十分条件でもない
\({\small (2)}~\)必要十分条件である
\({\small (3)}~\)十分条件である
\({\small (4)}~\)必要条件である
4
\({\small (1)}~\)必要条件でも十分条件でもない
\({\small (2)}~\)必要十分条件である
\({\small (3)}~\)十分条件である
\({\small (4)}~\)必要条件である
p.66
5
\({\small (1)}~\)

\(x<-2\) または \(0<x\)
\({\small (2)}~\)

\(2<x<3\)
\({\small (3)}~\)

\(0<x≦2\)
5
\({\small (1)}~\)
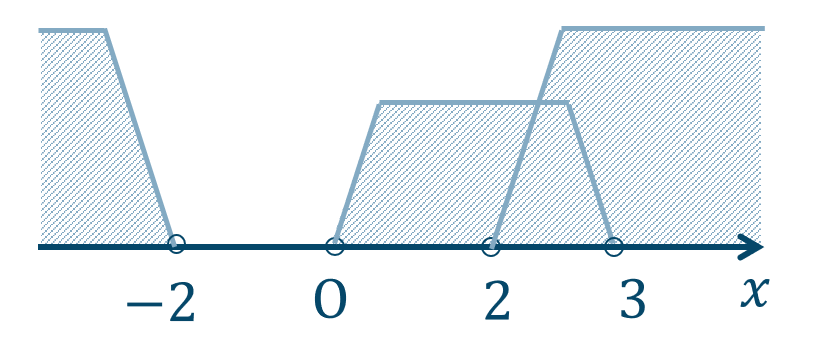
\(x<-2\) または \(0<x\)
\({\small (2)}~\)
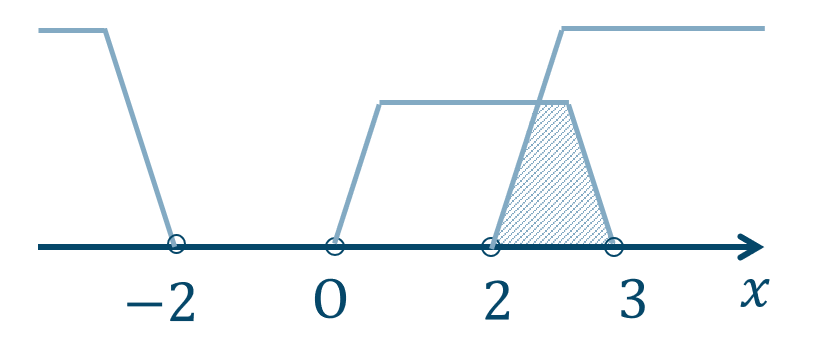
\(2<x<3\)
\({\small (3)}~\)
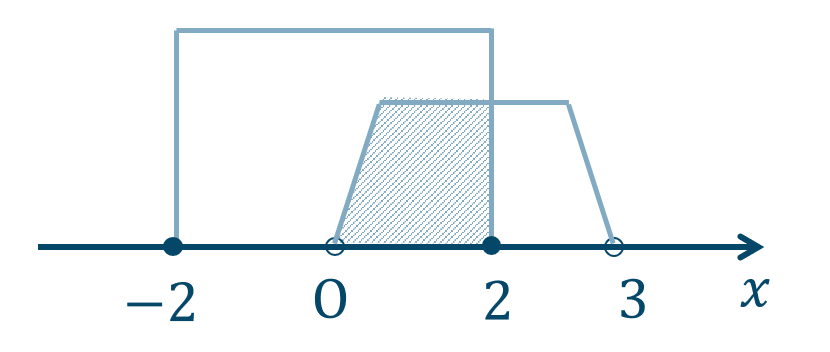
\(0<x≦2\)
p.66
6
[証明]この命題の対偶は、
\(n\) が偶数ならば \(n^2+1\) は奇数である
\(n\) が偶数より、整数 \(m\) を用いて \(n=2m\) とすると
\(n^2+1=(2m)^2+1\)
\(=4m^2+1=2\cdot2m+1\)
\(2m\) が整数より \(n^2\) は奇数である
したがって、対偶が真より
もとの命題も真となる[終]
6
[証明]この命題の対偶は、
\(n\) が偶数ならば \(n^2+1\) は奇数である
\(n\) が偶数より、整数 \(m\) を用いて \(n=2m\) とすると
\(n^2+1=(2m)^2+1\)
\(=4m^2+1=2\cdot2m+1\)
\(2m\) が整数より \(n^2\) は奇数である
したがって、対偶が真より
もとの命題も真となる[終]
p.66
7
[証明]\(x+\sqrt{3}\) が無理数でないと仮定すると
\(x+\sqrt{3}\) は有理数となり、有理数 \(r\) で表すことができる
\(x+\sqrt{3}=r\)
式変形すると、
\(\sqrt{3}=r-x\)
\(x~,~r\) が有理数であることより、\(r-x\) も有理数である
これより、この等式は \(\sqrt{3}\) が無理数であることに矛盾する
したがって、\(x+\sqrt{3}\) が無理数である[終]
7
[証明]\(x+\sqrt{3}\) が無理数でないと仮定すると
\(x+\sqrt{3}\) は有理数となり、有理数 \(r\) で表すことができる
\(x+\sqrt{3}=r\)
式変形すると、
\(\sqrt{3}=r-x\)
\(x~,~r\) が有理数であることより、\(r-x\) も有理数である
これより、この等式は \(\sqrt{3}\) が無理数であることに矛盾する
したがって、\(x+\sqrt{3}\) が無理数である[終]
Level Up 集合と論証
p.67
1
\({\small (1)}~{\rm A}\supset{\rm B}\) である
\({\small (2)}~{\rm A}\subset{\rm B}\) でも \({\rm A}\supset{\rm B}\) でもない
\({\small (3)}~{\rm A}={\rm B}\) である
1
\({\small (1)}~{\rm A}\supset{\rm B}\) である
\({\small (2)}~{\rm A}\subset{\rm B}\) でも \({\rm A}\supset{\rm B}\) でもない
\({\small (3)}~{\rm A}={\rm B}\) である
p.67
2
\({\rm B}=\{1,3,5,15\}\)
2
\({\rm B}=\{1,3,5,15\}\)
p.67
3
\({\small (1)}~\)ウ
\({\small (2)}~\)エ
\({\small (3)}~\)イ
\({\small (4)}~\)ア
3
\({\small (1)}~\)ウ
\({\small (2)}~\)エ
\({\small (3)}~\)イ
\({\small (4)}~\)ア
p.67
4
[証明]\(y\neq 0\) と仮定すると、\(x+y\sqrt{2}=0\) より
\(\sqrt{2}=-{\Large \frac{x}{y}}\)
ここて、\(x,y\) が有理数であることより、\(-{\large \frac{x}{y}}\) も有理数となる
これは、\(\sqrt{2}\) が無理数であることに矛盾する
よって、\(y=0\)
次にこれを \(x+y\sqrt{2}=0\) に代入すると、\(x=0\)
したがって、\(x,y\) が有理数で \(x+y\sqrt{2}=0~\Rightarrow~x=y=0\) [終]
4
[証明]\(y\neq 0\) と仮定すると、\(x+y\sqrt{2}=0\) より
\(\sqrt{2}=-{\Large \frac{x}{y}}\)
ここて、\(x,y\) が有理数であることより、\(-{\large \frac{x}{y}}\) も有理数となる
これは、\(\sqrt{2}\) が無理数であることに矛盾する
よって、\(y=0\)
次にこれを \(x+y\sqrt{2}=0\) に代入すると、\(x=0\)
したがって、\(x,y\) が有理数で \(x+y\sqrt{2}=0~\Rightarrow~x=y=0\) [終]
次のページ「3章 2次関数」


