文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 数と式
第2章 集合と命題
第3章 2次関数
第5章 データの分析
第4章 図形と計量
第1節 三角比
p.127
練習1
\({\small (1)}~\sin{\theta}={\large \frac{1}{\sqrt{5}}}~,~\cos{\theta}={\large \frac{2}{\sqrt{5}}}\)
\(\tan{\theta}={\large \frac{1}{2}}\)
\({\small (2)}~\sin{\theta}={\large \frac{5}{13}}~,~\cos{\theta}={\large \frac{12}{13}}\)
\(\tan{\theta}={\large \frac{5}{12}}\)
\({\small (3)}~\sin{\theta}={\large \frac{\sqrt{3}}{2}}~,~\cos{\theta}={\large \frac{1}{2}}\)
\(\tan{\theta}=\sqrt{3}\)
→ 直角三角形と三角比
練習1
\({\small (1)}~\sin{\theta}={\large \frac{1}{\sqrt{5}}}~,~\cos{\theta}={\large \frac{2}{\sqrt{5}}}\)
\(\tan{\theta}={\large \frac{1}{2}}\)
\({\small (2)}~\sin{\theta}={\large \frac{5}{13}}~,~\cos{\theta}={\large \frac{12}{13}}\)
\(\tan{\theta}={\large \frac{5}{12}}\)
\({\small (3)}~\sin{\theta}={\large \frac{\sqrt{3}}{2}}~,~\cos{\theta}={\large \frac{1}{2}}\)
\(\tan{\theta}=\sqrt{3}\)
→ 直角三角形と三角比
p.128
練習2
\({\small (1)}~\cos{30^\circ}={\large \frac{\sqrt{3}}{2}}~,~\tan{30^\circ}={\large \frac{1}{\sqrt{3}}}\)
\({\small (2)}~\sin{45^\circ}={\large \frac{1}{\sqrt{2}}}~,~\tan{45^\circ}=1\)
\({\small (3)}~\sin{60^\circ}={\large \frac{\sqrt{3}}{2}}~,~\cos{60^\circ}={\large \frac{1}{2}}\)
→ 三角比の値(鋭角)
練習2
\({\small (1)}~\cos{30^\circ}={\large \frac{\sqrt{3}}{2}}~,~\tan{30^\circ}={\large \frac{1}{\sqrt{3}}}\)
\({\small (2)}~\sin{45^\circ}={\large \frac{1}{\sqrt{2}}}~,~\tan{45^\circ}=1\)
\({\small (3)}~\sin{60^\circ}={\large \frac{\sqrt{3}}{2}}~,~\cos{60^\circ}={\large \frac{1}{2}}\)
→ 三角比の値(鋭角)
p.128
練習3
\({\small (1)}~0.4067\) \({\small (2)}~0.1219\)
\({\small (3)}~2.2460\)
練習3
\({\small (1)}~0.4067\) \({\small (2)}~0.1219\)
\({\small (3)}~2.2460\)
p.128
練習4
\({\small (1)}~15^\circ\) \({\small (2)}~58^\circ\) \({\small (3)}~77^\circ\)
練習4
\({\small (1)}~15^\circ\) \({\small (2)}~58^\circ\) \({\small (3)}~77^\circ\)
p.129
練習5
鉛直方向 \(171\) m、水平方向 \(470\) m
練習5
鉛直方向 \(171\) m、水平方向 \(470\) m
p.130
練習6
\(26.8\) m
練習6
\(26.8\) m
p.130
問1
約 \(5\) 度
問1
約 \(5\) 度
p.130
練習7
約 \(6\) 度
練習7
約 \(6\) 度
p.132
練習8
\({\small (1)}~\cos{\theta}={\large \frac{\sqrt{21}}{5}}~,~\tan{\theta}={\large \frac{2}{\sqrt{21}}}\)
\({\small (2)}~\sin{\theta}={\large \frac{\sqrt{7}}{4}}~,~\tan{\theta}={\large \frac{\sqrt{7}}{3}}\)
練習8
\({\small (1)}~\cos{\theta}={\large \frac{\sqrt{21}}{5}}~,~\tan{\theta}={\large \frac{2}{\sqrt{21}}}\)
\({\small (2)}~\sin{\theta}={\large \frac{\sqrt{7}}{4}}~,~\tan{\theta}={\large \frac{\sqrt{7}}{3}}\)
p.132
練習9
\(\cos{\theta}={\large \frac{2\sqrt{5}}{5}}~,~\sin{\theta}={\large \frac{\sqrt{5}}{5}}\)
→ 三角比の相互関係の公式(鋭角)
練習9
\(\cos{\theta}={\large \frac{2\sqrt{5}}{5}}~,~\sin{\theta}={\large \frac{\sqrt{5}}{5}}\)
→ 三角比の相互関係の公式(鋭角)
p.133
練習10
\({\small (1)}~\cos{16^\circ}\) \({\small (2)}~\sin{41^\circ}\)
\({\small (3)}~{\large \frac{1}{\tan{25^\circ}}}\)
→ 余角の公式
練習10
\({\small (1)}~\cos{16^\circ}\) \({\small (2)}~\sin{41^\circ}\)
\({\small (3)}~{\large \frac{1}{\tan{25^\circ}}}\)
→ 余角の公式
p.133
問2
[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\sin{{\frac{{\rm A}}{2}}}$$$$~=\sin{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\cos{{\frac{{\rm B+C}}{2}}}$$[終]
問2
[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\sin{{\frac{{\rm A}}{2}}}$$$$~=\sin{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\cos{{\frac{{\rm B+C}}{2}}}$$[終]
p.133
練習11
\({\small (1)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\cos{{\frac{{\rm A}}{2}}}$$$$~=\cos{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\sin{{\frac{{\rm B+C}}{2}}}$$[終]
\({\small (2)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\tan{{\frac{{\rm A}}{2}}}$$$$~=\tan{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\frac{1}{\tan{{\frac{{\rm B+C}}{2}}}}$$したがって、$$~\tan{\frac{{\rm A}}{2}}\tan{\frac{{\rm B+C}}{2}}=1$$[終]
練習11
\({\small (1)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\cos{{\frac{{\rm A}}{2}}}$$$$~=\cos{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\sin{{\frac{{\rm B+C}}{2}}}$$[終]
\({\small (2)}~\) [証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、$${\frac{\rm A}{2}}=90^\circ-{\frac{\rm B+C}{2}}$$これより、$$~~~~~~\tan{{\frac{{\rm A}}{2}}}$$$$~=\tan{\left(90^\circ-{\frac{{\rm B+C}}{2}}\right)}$$$$~=\frac{1}{\tan{{\frac{{\rm B+C}}{2}}}}$$したがって、$$~\tan{\frac{{\rm A}}{2}}\tan{\frac{{\rm B+C}}{2}}=1$$[終]
p.135
練習12
\({\small (1)}~\sin{135^\circ}={\large \frac{1}{\sqrt{2}}}~,~\cos{135^\circ}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{135^\circ}=-1\)
\({\small (2)}~\sin{150^\circ}={\large \frac{1}{2}}~,~\cos{150^\circ}=-{\large \frac{\sqrt{3}}{2}}\)
\(\tan{150^\circ}=-{\large \frac{1}{\sqrt{3}}}\)
→ 三角比の拡張
練習12
\({\small (1)}~\sin{135^\circ}={\large \frac{1}{\sqrt{2}}}~,~\cos{135^\circ}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{135^\circ}=-1\)
\({\small (2)}~\sin{150^\circ}={\large \frac{1}{2}}~,~\cos{150^\circ}=-{\large \frac{\sqrt{3}}{2}}\)
\(\tan{150^\circ}=-{\large \frac{1}{\sqrt{3}}}\)
→ 三角比の拡張
p.138
練習14
\({\small (1)}~45^\circ~,~135^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~120^\circ\) \({\small (4)}~0^\circ~,~180^\circ\)
練習14
\({\small (1)}~45^\circ~,~135^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~120^\circ\) \({\small (4)}~0^\circ~,~180^\circ\)
p.140
練習16
\({\small (1)}~\theta\) が鋭角のとき
\(\cos{\theta}={\large \frac{\sqrt{5}}{3}}~,~\tan{\theta}={\large \frac{2\sqrt{5}}{5}}\)
\(\theta\) が鈍角のとき
\(\cos{\theta}=-{\large \frac{\sqrt{5}}{3}}~,~\tan{\theta}=-{\large \frac{2\sqrt{5}}{5}}\)
\({\small (2)}~\sin{\theta}={\large \frac{\sqrt{15}}{4}}~,~\tan{\theta}=-\sqrt{15}\)
練習16
\({\small (1)}~\theta\) が鋭角のとき
\(\cos{\theta}={\large \frac{\sqrt{5}}{3}}~,~\tan{\theta}={\large \frac{2\sqrt{5}}{5}}\)
\(\theta\) が鈍角のとき
\(\cos{\theta}=-{\large \frac{\sqrt{5}}{3}}~,~\tan{\theta}=-{\large \frac{2\sqrt{5}}{5}}\)
\({\small (2)}~\sin{\theta}={\large \frac{\sqrt{15}}{4}}~,~\tan{\theta}=-\sqrt{15}\)
p.140
問3
\(\cos{\theta}=-{\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}={\large \frac{2}{\sqrt{5}}}\)
問3
\(\cos{\theta}=-{\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}={\large \frac{2}{\sqrt{5}}}\)
p.140
練習17
\({\small (1)}~\cos{\theta}=-{\large \frac{1}{\sqrt{3}}}~,~\sin{\theta}={\large \frac{\sqrt{6}}{3}}\)
\({\small (2)}~\cos{\theta}={\large \frac{3}{\sqrt{10}}}~,~\sin{\theta}={\large \frac{1}{\sqrt{10}}}\)
→ 三角比の相互関係の公式(鈍角)
練習17
\({\small (1)}~\cos{\theta}=-{\large \frac{1}{\sqrt{3}}}~,~\sin{\theta}={\large \frac{\sqrt{6}}{3}}\)
\({\small (2)}~\cos{\theta}={\large \frac{3}{\sqrt{10}}}~,~\sin{\theta}={\large \frac{1}{\sqrt{10}}}\)
→ 三角比の相互関係の公式(鈍角)
問題
p.142
1
\(53\) m
1
\(53\) m
p.142
2
\({\large \frac{1}{2+\sqrt{3}}}\)
2
\({\large \frac{1}{2+\sqrt{3}}}\)
p.142
3
\({\small (1)}~{\large \frac{a}{\tan{\theta}}}\) \({\small (2)}~{\large \frac{a}{\sin{\theta}}}\)
\({\small (3)}~a\cos{\theta}\)
3
\({\small (1)}~{\large \frac{a}{\tan{\theta}}}\) \({\small (2)}~{\large \frac{a}{\sin{\theta}}}\)
\({\small (3)}~a\cos{\theta}\)
p.142
4
1辺の長さ \(11.8\)
垂線の長さ \(8.1\)
4
1辺の長さ \(11.8\)
垂線の長さ \(8.1\)
p.142
5
\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\sin{(180^\circ-\theta)}=\sin{\theta}\) より、
\(\sin{(180^\circ-{\rm A})}=\sin{{\rm A}}\)
したがって、
\(\sin{{\rm A}}=\sin{({\rm B+C})}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\cos{(180^\circ-\theta)}=-\cos{\theta}\) より、
\(\cos{(180^\circ-{\rm A})}=-\cos{{\rm A}}\)
したがって、
\(\cos{{\rm A}}=-\cos{({\rm B+C})}\) [終]
5
\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\sin{(180^\circ-\theta)}=\sin{\theta}\) より、
\(\sin{(180^\circ-{\rm A})}=\sin{{\rm A}}\)
したがって、
\(\sin{{\rm A}}=\sin{({\rm B+C})}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) の内角の和の条件より、
\({\rm A+B+C}=180^\circ\)
よって、
\({\rm B+C}=180^\circ-{\rm A}\)
ここで、\(\cos{(180^\circ-\theta)}=-\cos{\theta}\) より、
\(\cos{(180^\circ-{\rm A})}=-\cos{{\rm A}}\)
したがって、
\(\cos{{\rm A}}=-\cos{({\rm B+C})}\) [終]
p.142
6
\(75^\circ\)
6
\(75^\circ\)
第2節 三角形への応用
p.145
練習19
\({\small (1)}~6\sqrt{2}\) \({\small (2)}~2\sqrt{6}\)
練習19
\({\small (1)}~6\sqrt{2}\) \({\small (2)}~2\sqrt{6}\)
p.145
練習20
\({\small (1)}~{\large \frac{8\sqrt{3}}{3}}\)
\({\small (2)}~30^\circ~,~150^\circ\)
→ 正弦定理
練習20
\({\small (1)}~{\large \frac{8\sqrt{3}}{3}}\)
\({\small (2)}~30^\circ~,~150^\circ\)
→ 正弦定理
p.148
練習23
\(150^\circ\)
練習23
\(150^\circ\)
p.149
練習24
\({\rm A}\) は鋭角
\({\rm B}\) は鋭角
\({\rm C}\) は鈍角
練習24
\({\rm A}\) は鋭角
\({\rm B}\) は鋭角
\({\rm C}\) は鈍角
p.150
練習26
\(a=2\sqrt{2}~,~{\rm B}=30^\circ~,~{\rm C}=105^\circ\)
練習26
\(a=2\sqrt{2}~,~{\rm B}=30^\circ~,~{\rm C}=105^\circ\)
p.151
練習27
\(a=\sqrt{3}+1~,~{\rm A}=105^\circ~,~{\rm B}=45^\circ\)
または
\(a=\sqrt{3}-1~,~{\rm A}=15^\circ~,~{\rm B}=135^\circ\)
練習27
\(a=\sqrt{3}+1~,~{\rm A}=105^\circ~,~{\rm B}=45^\circ\)
または
\(a=\sqrt{3}-1~,~{\rm A}=15^\circ~,~{\rm B}=135^\circ\)
p.152
練習28
\(\cos{{\rm C}}={\large \frac{13}{14}}\)
練習28
\(\cos{{\rm C}}={\large \frac{13}{14}}\)
p.153
発展1
\({\small (1)}~a=b\) の二等辺三角形
\({\small (2)}~b=c\) の二等辺三角形
\({\small (3)}~a=b\) の二等辺三角形
または \({\rm C}=90^\circ\) の直角三角形
発展1
\({\small (1)}~a=b\) の二等辺三角形
\({\small (2)}~b=c\) の二等辺三角形
\({\small (3)}~a=b\) の二等辺三角形
または \({\rm C}=90^\circ\) の直角三角形
p.155
練習30
\({\large \frac{3\sqrt{15}}{4}}\)
練習30
\({\large \frac{3\sqrt{15}}{4}}\)
p.159
練習35
\({\small (1)}~{\large \frac{1}{\sqrt{3}}}\) \({\small (2)}~{\large \frac{\sqrt{2}}{4}}a^2\)
→ 正四面体の計量
練習35
\({\small (1)}~{\large \frac{1}{\sqrt{3}}}\) \({\small (2)}~{\large \frac{\sqrt{2}}{4}}a^2\)
→ 正四面体の計量
p.160
練習36
\(5\sqrt{3}\)
練習36
\(5\sqrt{3}\)
p.161
練習37
\(40\sqrt{6}\) m
練習37
\(40\sqrt{6}\) m
問題
p.162
7
\(100\sqrt{7}\) m
7
\(100\sqrt{7}\) m
p.162
8
\({\small (1)}~\)[証明]

図より、
\({\rm BH}=c\cos{{\rm B}}\)
\({\rm CH}=b\cos{{\rm C}}\)
ここで、\({\rm BC=BH+HC}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (2)}~\)[証明]

図より、
\({\rm BH}=c\cos{(180^\circ-{\rm B})}\)
\(=-c\cos{{\rm B}}\)
\({\rm CH}=b\cos{{\rm C}}\)
ここで、\({\rm BC=CH-BH}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (3)}~\)[証明]

図より、
\({\rm BH}=c\cos{{\rm B}}\)
\({\rm CH}=b\cos{(180^\circ-{\rm C})}\)
\(=-b\cos{{\rm C}}\)
ここで、\({\rm BC=BH-CH}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (4)}~\)[証明]

図より、
\(\cos{{\rm B}}=\cos{90^\circ}=0\)
\({\rm BC}=b\cos{{\rm C}}\)
よって、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
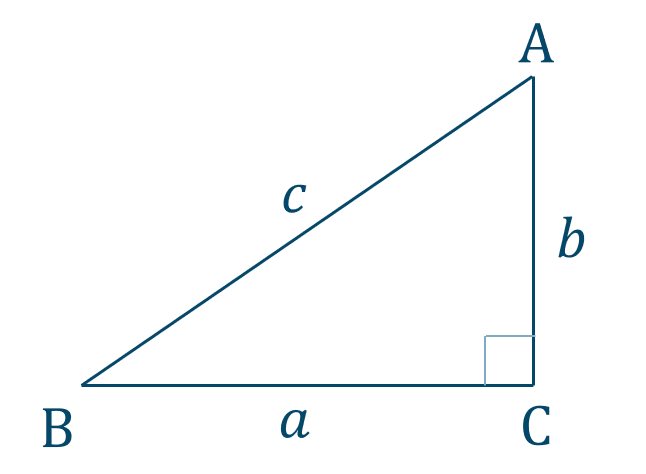
\({\small (5)}~\)[証明]

図より、
\(\cos{{\rm C}}=\cos{90^\circ}=0\)
\({\rm BC}=c\cos{{\rm B}}\)
よって、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
8
\({\small (1)}~\)[証明]
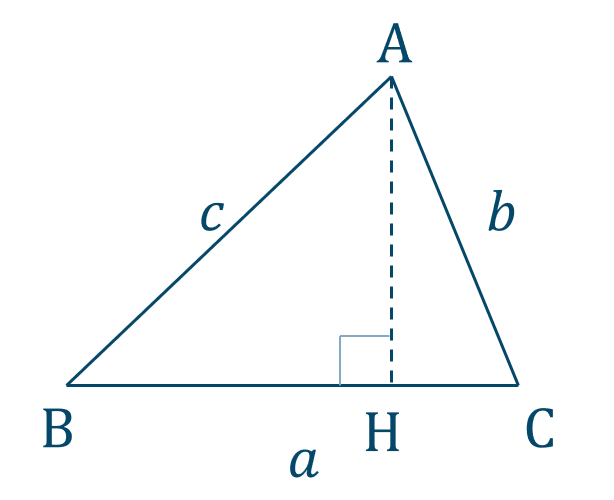
図より、
\({\rm BH}=c\cos{{\rm B}}\)
\({\rm CH}=b\cos{{\rm C}}\)
ここで、\({\rm BC=BH+HC}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (2)}~\)[証明]
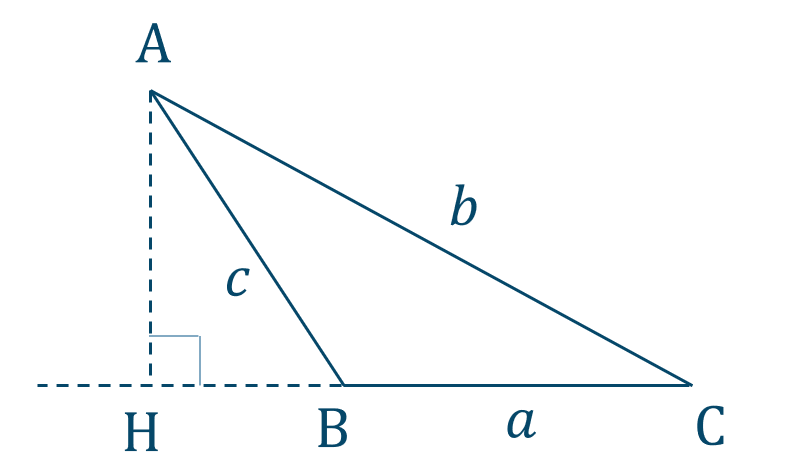
図より、
\({\rm BH}=c\cos{(180^\circ-{\rm B})}\)
\(=-c\cos{{\rm B}}\)
\({\rm CH}=b\cos{{\rm C}}\)
ここで、\({\rm BC=CH-BH}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (3)}~\)[証明]
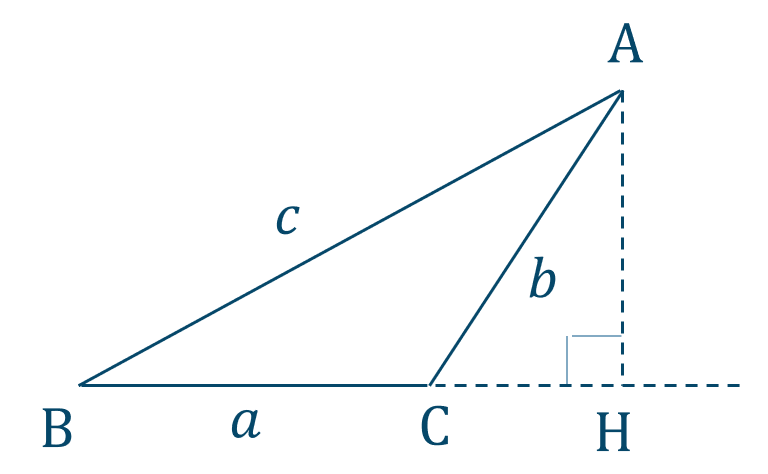
図より、
\({\rm BH}=c\cos{{\rm B}}\)
\({\rm CH}=b\cos{(180^\circ-{\rm C})}\)
\(=-b\cos{{\rm C}}\)
ここで、\({\rm BC=BH-CH}\) より、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (4)}~\)[証明]
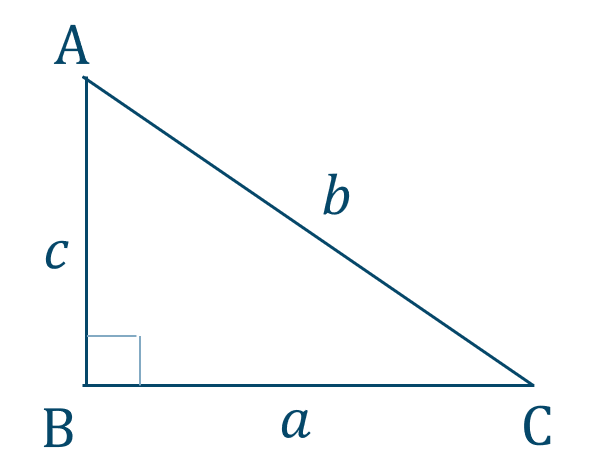
図より、
\(\cos{{\rm B}}=\cos{90^\circ}=0\)
\({\rm BC}=b\cos{{\rm C}}\)
よって、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
\({\small (5)}~\)[証明]
図より、
\(\cos{{\rm C}}=\cos{90^\circ}=0\)
\({\rm BC}=c\cos{{\rm B}}\)
よって、
\(a=b\cos{{\rm C}}+c\cos{{\rm B}}\) [終]
p.162
9
\({\small (1)}~{\large \frac{\sqrt{13}}{2}}\) \({\small (2)}~{\large \frac{5}{2\sqrt{13}}}\) \({\small (3)}~{\large \frac{\sqrt{37}}{2}}\)
9
\({\small (1)}~{\large \frac{\sqrt{13}}{2}}\) \({\small (2)}~{\large \frac{5}{2\sqrt{13}}}\) \({\small (3)}~{\large \frac{\sqrt{37}}{2}}\)
p.162
10
\(2\sqrt{2}\)
10
\(2\sqrt{2}\)
p.162
11
\(3\sqrt{5}\)
11
\(3\sqrt{5}\)
演習問題 図形と計量
演習問題A
p.163
1
\({\small (1)}~\)[証明] \({\rm AC=CD}\) より、\(\triangle {\rm ADC}\) は直角二等辺三角形であり
\(\angle{\rm DAC}=45^\circ\)
また、\(\triangle {\rm ABC}\) において、
\(\angle{\rm BAC}=180^\circ-(90^\circ+30^\circ)\)
\(=60^\circ\)
よって、
\(\angle{\rm BAD}=\angle{\rm BAC}-\angle{\rm DAC}=15^\circ\) [終]
\({\small (2)}~{\rm AB}=2~,~{\rm AD}=\sqrt{2}\)
\(~,~{\rm BD}=\sqrt{3}-1\)
\({\small (3)}~\)
\(\sin{15^\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}\)
\(\cos{15^\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}\)
1
\({\small (1)}~\)[証明] \({\rm AC=CD}\) より、\(\triangle {\rm ADC}\) は直角二等辺三角形であり
\(\angle{\rm DAC}=45^\circ\)
また、\(\triangle {\rm ABC}\) において、
\(\angle{\rm BAC}=180^\circ-(90^\circ+30^\circ)\)
\(=60^\circ\)
よって、
\(\angle{\rm BAD}=\angle{\rm BAC}-\angle{\rm DAC}=15^\circ\) [終]
\({\small (2)}~{\rm AB}=2~,~{\rm AD}=\sqrt{2}\)
\(~,~{\rm BD}=\sqrt{3}-1\)
\({\small (3)}~\)
\(\sin{15^\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}\)
\(\cos{15^\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}\)
p.163
2
[証明]

\(\angle{\rm AMB}=\theta\) とすると、
\(\angle{\rm AMC}=180^\circ-\theta\)
\(\triangle {\rm ABM}\) において、余弦定理より、
\({\rm AB^2=AM^2+CM^2}\)
\(-2{\rm AM\cdot CM} \cos{\theta}\) …①
\(\triangle {\rm ACM}\) において、余弦定理より、
\({\rm AC^2=AM^2+BM^2}\)
\(-2{\rm AM\cdot BM} \cos{(180^\circ-\theta})\)
ここで、\(\cos{(180^\circ-\theta)=-\cos{\theta}}\)
\(~,~{\rm BM=CM}\) より
\({\rm AB^2=AM^2+BM^2}\)
\(-2{\rm AM\cdot BM} \cos{\theta}\) …②
①と②の両辺を加えると、
\({\rm AB^2+AC^2}=2({\rm AM^2+BM^2})\) [終]
2
[証明]
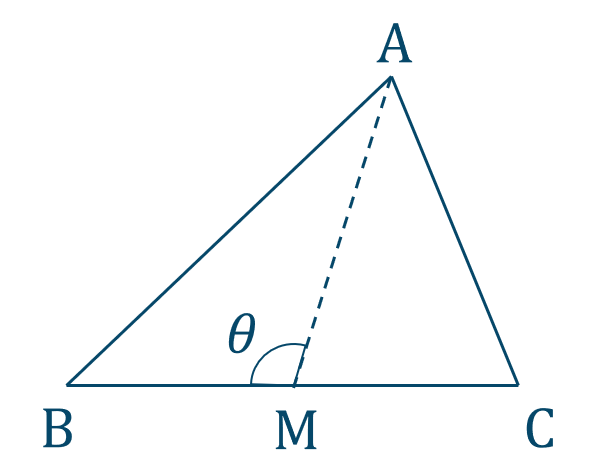
\(\angle{\rm AMB}=\theta\) とすると、
\(\angle{\rm AMC}=180^\circ-\theta\)
\(\triangle {\rm ABM}\) において、余弦定理より、
\({\rm AB^2=AM^2+CM^2}\)
\(-2{\rm AM\cdot CM} \cos{\theta}\) …①
\(\triangle {\rm ACM}\) において、余弦定理より、
\({\rm AC^2=AM^2+BM^2}\)
\(-2{\rm AM\cdot BM} \cos{(180^\circ-\theta})\)
ここで、\(\cos{(180^\circ-\theta)=-\cos{\theta}}\)
\(~,~{\rm BM=CM}\) より
\({\rm AB^2=AM^2+BM^2}\)
\(-2{\rm AM\cdot BM} \cos{\theta}\) …②
①と②の両辺を加えると、
\({\rm AB^2+AC^2}=2({\rm AM^2+BM^2})\) [終]
p.163
3
\(\cos{{\rm A}}=\frac{7}{8}~,~\sin{{\rm A}}=\frac{\sqrt{15}}{8}\)
\(\tan{{\rm A}}=\frac{\sqrt{15}}{7}\)
3
\(\cos{{\rm A}}=\frac{7}{8}~,~\sin{{\rm A}}=\frac{\sqrt{15}}{8}\)
\(\tan{{\rm A}}=\frac{\sqrt{15}}{7}\)
p.163
4
[証明]

\(\triangle {\rm AOD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(\triangle {\rm AOB}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(\triangle {\rm BOC}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(\triangle {\rm OCD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
これら4つの三角形の面積の和が、四角形の面積 \(S\) となるので、
\(S= {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(+ {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(~+{\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(~~+ {\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
因数分解すると、
\(S={\large \frac{1}{2}}({\rm OA+OC})({\rm OB+OD})\sin{\theta}\)
ここで、\({\rm OA+OC}=a\)
\(~,~{\rm OB+OD}=b\) より、
\(S={\large \frac{1}{2}}ab\sin{\theta}\) [終]
4
[証明]
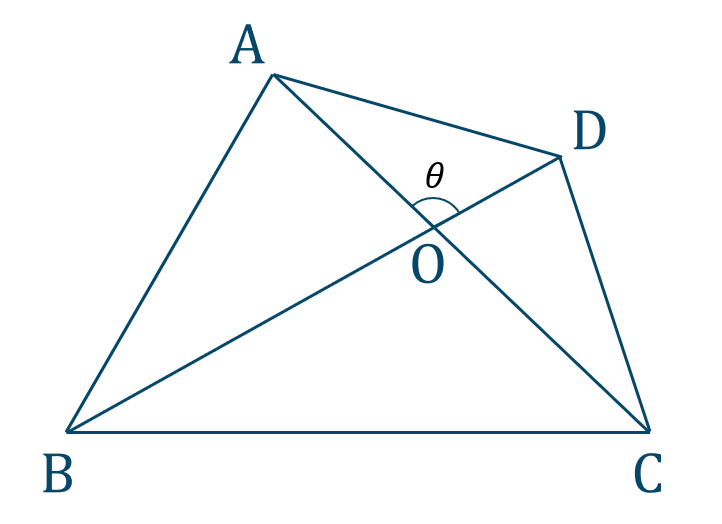
\(\triangle {\rm AOD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(\triangle {\rm AOB}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(\triangle {\rm BOC}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(\triangle {\rm OCD}\) の面積は
\({\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{(180^\circ-\theta)}\)
\(={\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
これら4つの三角形の面積の和が、四角形の面積 \(S\) となるので、
\(S= {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OD}\sin{\theta}\)
\(+ {\large \frac{1}{2}}\cdot{\rm OA}\cdot{\rm OB}\sin{\theta}\)
\(~+{\large \frac{1}{2}}\cdot{\rm OB}\cdot{\rm OC}\sin{\theta}\)
\(~~+ {\large \frac{1}{2}}\cdot{\rm OC}\cdot{\rm OD}\sin{\theta}\)
因数分解すると、
\(S={\large \frac{1}{2}}({\rm OA+OC})({\rm OB+OD})\sin{\theta}\)
ここで、\({\rm OA+OC}=a\)
\(~,~{\rm OB+OD}=b\) より、
\(S={\large \frac{1}{2}}ab\sin{\theta}\) [終]
p.163
5
\({\small (1)}~\)[証明] 正弦定理より、
\(b=2R\sin{{\rm B}}\) …①
\(c=2R\sin{{\rm C}}\) …②
ここで、面積 \(S\) は、
\(S=\frac{1}{2}bc\sin{{\rm A}}\)
①と②を代入すると、
\(S=2R^2\sin{{\rm A}}\cdot\sin{{\rm B}}\cdot\sin{{\rm C}}\) [終]
\({\small (2)}~\)[証明] 正弦定理より、
\(\sin{{\rm A}}=\frac{a}{2R}\) …①
ここで、面積 \(S\) は、
\(S=\frac{1}{2}bc\sin{{\rm A}}\)
①を代入すると、
\(S=\frac{abc}{4R}\) [終]
5
\({\small (1)}~\)[証明] 正弦定理より、
\(b=2R\sin{{\rm B}}\) …①
\(c=2R\sin{{\rm C}}\) …②
ここで、面積 \(S\) は、
\(S=\frac{1}{2}bc\sin{{\rm A}}\)
①と②を代入すると、
\(S=2R^2\sin{{\rm A}}\cdot\sin{{\rm B}}\cdot\sin{{\rm C}}\) [終]
\({\small (2)}~\)[証明] 正弦定理より、
\(\sin{{\rm A}}=\frac{a}{2R}\) …①
ここで、面積 \(S\) は、
\(S=\frac{1}{2}bc\sin{{\rm A}}\)
①を代入すると、
\(S=\frac{abc}{4R}\) [終]
p.163
6
\(\frac{7\sqrt{55}}{4}\)
6
\(\frac{7\sqrt{55}}{4}\)
演習問題B
p.164
7
\({\small (1)}~\frac{3\sqrt{5}}{5}\) \({\small (2)}~\frac{1}{\sqrt{10}}\)
7
\({\small (1)}~\frac{3\sqrt{5}}{5}\) \({\small (2)}~\frac{1}{\sqrt{10}}\)
p.164
8
[証明] 図より、
\(\triangle {\rm OAP}=\frac{1}{2}ap\sin{\alpha}\)
\(\triangle {\rm OBP}=\frac{1}{2}bp\sin{\beta}\)
また、\(\triangle {\rm OAB}\) の面積は、
\(\triangle {\rm OAB}=\frac{1}{2}ab\sin{(\alpha+\beta)}\)
ここで、\(\triangle {\rm OAP}+\triangle {\rm OBP}=\triangle {\rm OAB}\) より、
\(\frac{1}{2}ap\sin{\alpha}+ \frac{1}{2}bp\sin{\beta}\)
\(= \frac{1}{2}ab\sin{(\alpha+\beta)}\)
\({\large \frac{2}{abp}}\) を両辺にかけると、
\(\frac{\sin{\alpha}}{a}+\frac{\sin{\beta}}{b}=\frac{\sin{(\alpha+\beta)}}{p}\) [終]
8
[証明] 図より、
\(\triangle {\rm OAP}=\frac{1}{2}ap\sin{\alpha}\)
\(\triangle {\rm OBP}=\frac{1}{2}bp\sin{\beta}\)
また、\(\triangle {\rm OAB}\) の面積は、
\(\triangle {\rm OAB}=\frac{1}{2}ab\sin{(\alpha+\beta)}\)
ここで、\(\triangle {\rm OAP}+\triangle {\rm OBP}=\triangle {\rm OAB}\) より、
\(\frac{1}{2}ap\sin{\alpha}+ \frac{1}{2}bp\sin{\beta}\)
\(= \frac{1}{2}ab\sin{(\alpha+\beta)}\)
\({\large \frac{2}{abp}}\) を両辺にかけると、
\(\frac{\sin{\alpha}}{a}+\frac{\sin{\beta}}{b}=\frac{\sin{(\alpha+\beta)}}{p}\) [終]
p.164
9
\({\small (1)}~14\) \({\small (2)}~\frac{12}{7}\)
9
\({\small (1)}~14\) \({\small (2)}~\frac{12}{7}\)
p.164
10
\({\small (1)}~\frac{\sqrt{2}}{12}a^3\)
\({\small (2)}~\)[証明] この正四面体を球の中心を頂点とする4つの三角錐に分けると、
\(V=\frac{1}{3}r\triangle {\rm ABC}+\frac{1}{3}r\triangle {\rm ACD}\)
\(~~~~~~+\frac{1}{3}r\triangle {\rm ABD}+\frac{1}{3}r\triangle {\rm BCD}\)
ここで、表面積 \(S\) は、
\(S=\triangle {\rm ABC}+\triangle {\rm ACD}\)
\(+\triangle {\rm ABD}+\triangle {\rm BCD}\)
よって、
\(V=\frac{1}{3}rS\) [終]
\({\small (3)}~\)
\(r=\frac{\sqrt{6}}{12}a~,~V=\frac{\sqrt{6}}{216}\pi a^3\)
10
\({\small (1)}~\frac{\sqrt{2}}{12}a^3\)
\({\small (2)}~\)[証明] この正四面体を球の中心を頂点とする4つの三角錐に分けると、
\(V=\frac{1}{3}r\triangle {\rm ABC}+\frac{1}{3}r\triangle {\rm ACD}\)
\(~~~~~~+\frac{1}{3}r\triangle {\rm ABD}+\frac{1}{3}r\triangle {\rm BCD}\)
ここで、表面積 \(S\) は、
\(S=\triangle {\rm ABC}+\triangle {\rm ACD}\)
\(+\triangle {\rm ABD}+\triangle {\rm BCD}\)
よって、
\(V=\frac{1}{3}rS\) [終]
\({\small (3)}~\)
\(r=\frac{\sqrt{6}}{12}a~,~V=\frac{\sqrt{6}}{216}\pi a^3\)
次のページ「第5章 データの分析」


