文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第5章 指数関数と対数関数
第6章 微分法と積分法
このページは非常に重くなるのでレイアウトを変更しております。
第4章 三角関数
第1節 三角関数
\(780^\circ~,~-300^\circ\)
\({\small (1)}~{\large \frac{\pi}{12}}\) \({\small (2)}~{\large \frac{7}{6}}\pi\)
\({\small (3)}~-{\large \frac{4}{3}}\pi\) \({\small (4)}~{\large \frac{7}{4}}\pi\)
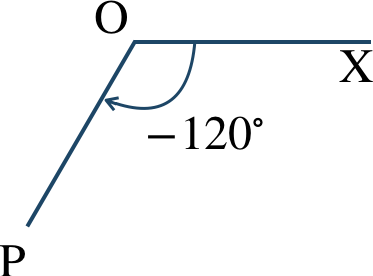
\({\small (1)}~225^\circ\) \({\small (2)}~288^\circ\)
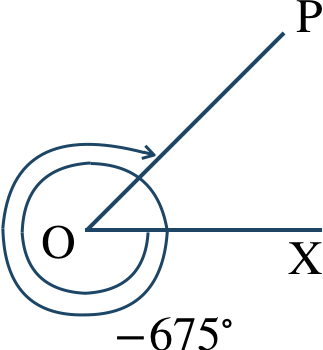
\({\small (3)}~-450^\circ\) \({\small (4)}~75^\circ\)
\({\small (1)}~l={\large \frac{4}{5}}\pi~,~S={\large \frac{8}{5}}\pi\)
\({\small (2)}~l=5\pi~,~S=15\pi\)
→ 弧度法と扇形
\({\small (1)}~\)
\(\sin{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{2}}\)
\(\cos{{\large \frac{11}{6}}\pi}={\large \frac{\sqrt{3}}{2}}\)
\(\tan{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{\sqrt{3}}}\)
\({\small (2)}~\)
\(\sin{\left(-{\large \frac{5}{4}}\pi\right)}={\large \frac{1}{\sqrt{2}}}\)
\(\cos{\left(-{\large \frac{5}{4}}\pi\right)}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{\left(-{\large \frac{5}{4}}\pi\right)}=-1\)
\({\small (3)}~\)
\(\sin{{\large \frac{10}{3}}\pi}=-{\large \frac{\sqrt{3}}{2}}\)
\(\cos{{\large \frac{10}{3}}\pi}=-{\large \frac{1}{2}}\)
\(\tan{{\large \frac{10}{3}}\pi}=\sqrt{3}\)
\({\small (4)}~\)
\(\sin{(-3\pi)}=0~,~\cos{(-3\pi)}=-1\)
\(\tan{(-3\pi)}=0\)
→ 三角関数の値(単位円)
\(\sin{\theta}=-{\large \frac{12}{13}}~,~\tan{\theta}=-{\large \frac{12}{5}}\)
\(\cos{\theta}={\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}=-{\large \frac{2}{\sqrt{5}}}\)
または
\(\cos{\theta}=-{\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}={\large \frac{2}{\sqrt{5}}}\)
\(\cos{\theta}={\large \frac{3}{\sqrt{10}}}~,~\sin{\theta}={\large \frac{1}{\sqrt{10}}}\)
または
\(\cos{\theta}=-{\large \frac{3}{\sqrt{10}}}~,~\sin{\theta}=-{\large \frac{1}{\sqrt{10}}}\)
→ 三角関数の相互関係の公式
\({\small (1)}~\)[証明]
(左辺)
\(=\sin^2{\theta}+2\sin{\theta}\cos{\theta}+\cos^2{\theta}\)
\(+\sin^2{\theta}-2\sin{\theta}\cos{\theta}+\cos^2{\theta}\)
\(=2(\sin^2{\theta}+\cos^2{\theta})=2\)
したがって、
\((\sin{\theta}+\cos{\theta})^2\)
\(+(\sin{\theta}-\cos{\theta})^2=2\)
[終]
\({\small (2)}~\)[証明]
\(\tan{\theta}={\large \frac{\sin{\theta}}{\cos{\theta}}}\) より、
(左辺)$$~=\frac{\sin^2{\theta}}{\cos^2{\theta}}+\left(1-\frac{\sin^4{\theta}}{\cos^4{\theta}}\right)\cos^2{\theta}$$$$~=\frac{\sin^2{\theta}}{\cos^2{\theta}}+\cos^2{\theta}-\frac{\sin^4{\theta}}{\cos^2{\theta}}$$$$~=\frac{\sin^2{\theta}(1-\sin^2{\theta})}{\cos^2{\theta}}+\cos^2{\theta}$$ここで、\(1-\sin^2{\theta}=\cos^2{\theta}\) より、$$~=\frac{\sin^2{\theta}\cos^2{\theta}}{\cos^2{\theta}}+\cos^2{\theta}$$$$~=\sin^2{\theta}+\cos^2{\theta}=1$$したがって、
\(\tan^2{\theta}+(1-\tan^4{\theta})\cos^2{\theta}=1\)
[終]
→ 三角関数の等式の証明
\({\small (1)}~{\large \frac{1-a^2}{2}}\) \({\small (2)}~{\large \frac{a(3-a^2)}{2}}\)
→ 三角関数の式の値
\({\small (1)}~{\large \frac{\sqrt{3}}{2}}\) \({\small (2)}~0\) \({\small (3)}~1\)
\({\small (1)}~-{\large \frac{1}{2}}\) \({\small (2)}~{\large \frac{1}{\sqrt{2}}}\) \({\small (3)}~-\sqrt{3}\)
\({\small (1)}~-{\large \frac{1}{\sqrt{2}}}\) \({\small (2)}~-{\large \frac{\sqrt{3}}{2}}\) \({\small (3)}~{\large \frac{1}{\sqrt{3}}}\)
→ 三角関数の性質①
公式3’
[証明]
\(\sin{(\pi-\theta)}\)
\(=\sin{\{\pi+(-\theta)\}}\)
\(=-\sin{(-\theta)}=\sin{\theta}\)
\(\cos{(\pi-\theta)}\)
\(=\cos{\{\pi+(-\theta)\}}\)
\(=-\cos{(-\theta)}=-\cos{\theta}\)
\(\tan{(\pi-\theta)}\)
\(=\tan{\{\pi+(-\theta)\}}\)
\(=\tan{(-\theta)}=-\tan{\theta}\)
[終]
公式4’
[証明]
\(\sin{\left({\large \frac{\pi}{2}}-\theta\right)}\)
\(=\sin{\left\{{\large \frac{\pi}{2}}+(-\theta)\right\}}\)
\(=\cos{(-\theta)}=\cos{\theta}\)
\(\cos{\left({\large \frac{\pi}{2}}-\theta\right)}\)
\(=\cos{\left\{{\large \frac{\pi}{2}}+(-\theta)\right\}}\)
\(=-\sin{(-\theta)}=\sin{\theta}\)
\(\tan{\left({\large \frac{\pi}{2}}-\theta\right)}\)
\(=\tan{\left\{{\large \frac{\pi}{2}}+(-\theta)\right\}}\)
\(=-{\large \frac{1}{\tan{(-\theta)}}}={\large \frac{1}{\tan{\theta}}}\)
[終]
\({\small (1)}~\)
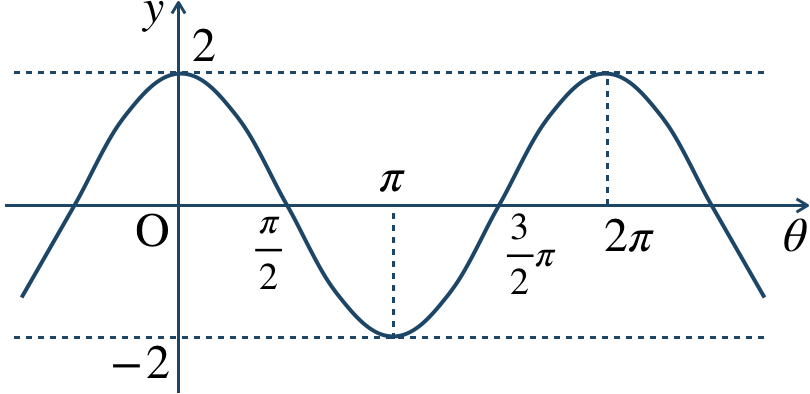
周期 \(2\pi\)
\({\small (2)}~\)
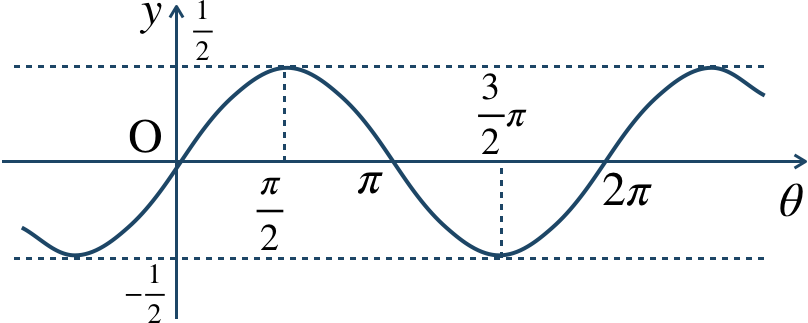
周期 \(2\pi\)
\({\small (3)}~\)
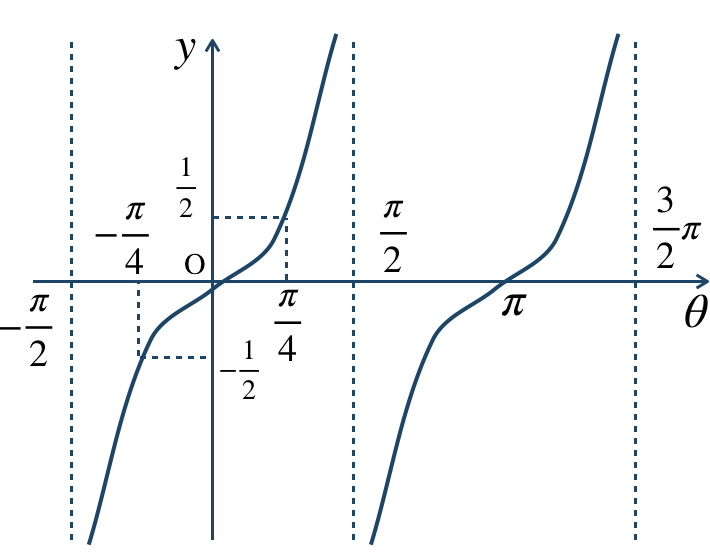
周期 \(\pi\)
→ 三角関数のグラフ①
→ 三角関数のグラフ②(縦幅の変化)
\({\small (1)}~\)

周期 \(2\pi\)
\({\small (2)}~\)
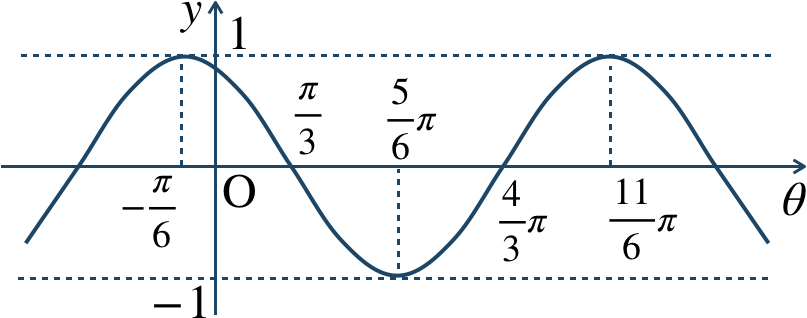
周期 \(2\pi\)
\({\small (3)}~\)
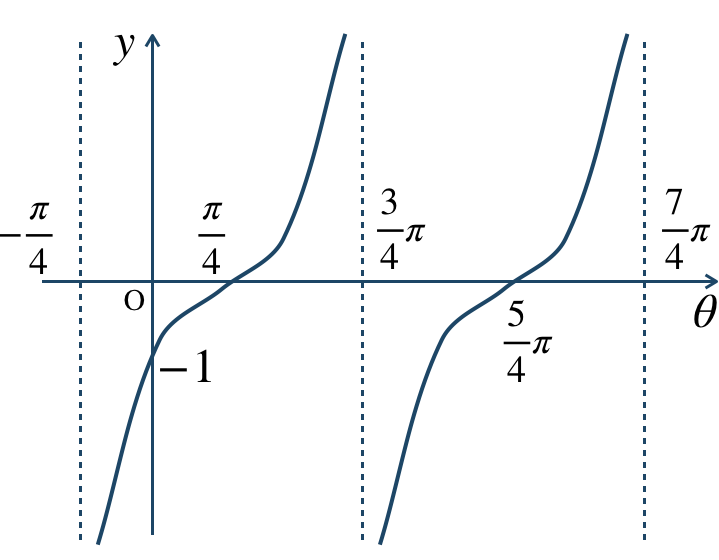
周期 \(\pi\)
→ 三角関数のグラフ④(平行移動)
\({\small (1)}~\)
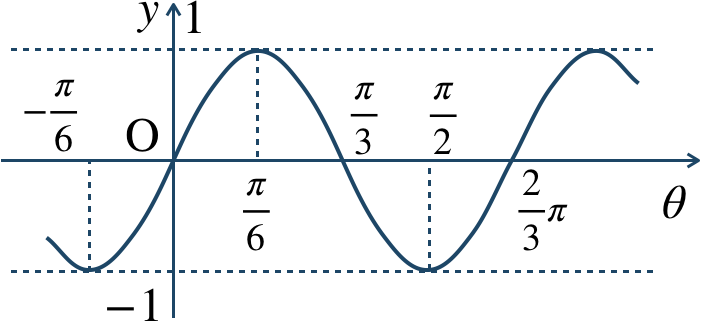
周期 \({\large \frac{2}{3}}\pi\)
\({\small (2)}~\)
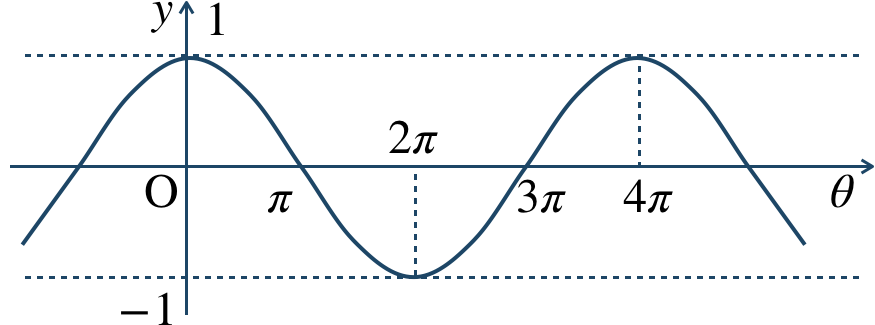
周期 \(4\pi\)
\({\small (3)}~\)
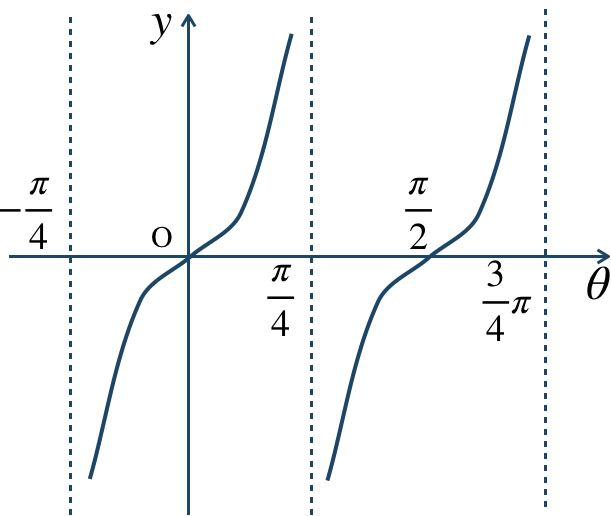
周期 \({\large \frac{\pi}{2}}\)
→ 三角関数のグラフ③(周期の変化)
\({\small (1)}~\theta={\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi\)
\(n\) を整数として、
\(\theta={\large \frac{\pi}{6}}+2n\pi~,~{\large \frac{5}{6}}\pi+2n\pi\)
\({\small (2)}~\theta={\large \frac{5}{6}}\pi~,~{\large \frac{7}{6}}\pi\)
\(n\) を整数として、
\(\theta={\large \frac{5}{6}}\pi+2n\pi~,~{\large \frac{7}{6}}\pi+2n\pi\)
[証明]
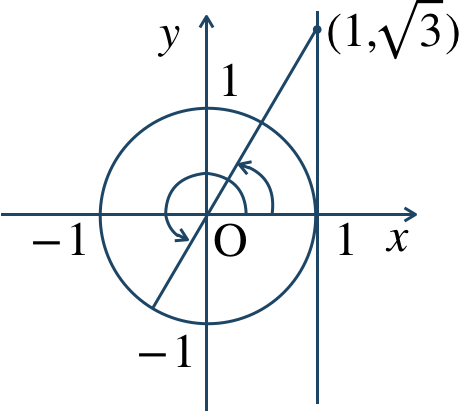
図の単位円より、求める \(\theta\) の値は動径の表す角であり、 \(0≦\theta<2\pi\) の範囲では、
\(\theta={\large \frac{\pi}{3}}~,~{\large \frac{4}{3}}\pi\)
よって、\(\theta\) に制限がないときは周期 \(\pi\) の間隔で値をとる
したがって、求める解は整数 \(n\) を用いて、
\(\theta={\large \frac{\pi}{3}}+n\pi\) [終]
\(\theta={\large \frac{\pi}{4}}~,~{\large \frac{5}{4}}\pi\)
\(n\) を整数として、
\(\theta={\large \frac{\pi}{4}}+n\pi\)
→ 三角関数を含む方程式①
\({\small (1)}~{\large \frac{4}{3}}\pi<\theta<{\large \frac{5}{3}}\pi\)
\({\small (2)}~0≦\theta≦{\large \frac{\pi}{4}}~,~{\large \frac{7}{4}}\pi≦\theta<2\pi\)
\(0≦\theta<{\large \frac{\pi}{3}}~,~{\large \frac{\pi}{2}}<\theta<{\large \frac{4}{3}}\pi\)
\({\large \frac{3}{2}}\pi<\theta<2\pi\)
\({\large \frac{\pi}{4}}≦\theta<{\large \frac{\pi}{2}}~,~{\large \frac{5}{4}}\pi≦\theta<{\large \frac{3}{2}}\pi\)
→ 三角関数を含む不等式①
\({\small (1)}~\theta={\large \frac{\pi}{6}}~,~{\large \frac{\pi}{2}}\)
\({\small (2)}~\theta={\large \frac{13}{12}}\pi~,~{\large \frac{19}{12}}\pi\)
\({\small (3)}~\theta={\large \frac{7}{12}}\pi~,~{\large \frac{23}{12}}\pi\)
\({\small (2)}~\theta={\large \frac{\pi}{12}}~,~{\large \frac{13}{12}}\pi\)
→ 三角関数を含む方程式②(範囲変化)
\(0≦\theta≦{\large \frac{5}{12}}\pi~,~{\large \frac{23}{12}}\pi≦\theta<2\pi\)
\({\small (1)}~0≦\theta≦{\large \frac{\pi}{6}}~,~{\large \frac{3}{2}}\pi≦\theta<2\pi\)
\({\small (2)}~0≦\theta<{\large \frac{7}{12}}\pi~,~{\large \frac{11}{12}}\pi<\theta<2\pi\)
\({\small (3)}~{\large \frac{\pi}{12}}<\theta<{\large \frac{\pi}{4}}~,~{\large \frac{13}{12}}\pi<\theta<{\large \frac{5}{4}}\pi\)
→ 三角関数を含む不等式②(範囲変化)
\(\theta={\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi\) で最大値 \({\large \frac{5}{4}}\)
\(\theta=0\) で最大値 \(-1\)
→ 三角関数を含む2次関数
問題
\({\small (1)}~-{\large \frac{1}{2}}\) \({\small (2)}~-{\large \frac{1}{\sqrt{2}}}\) \({\small (3)}~-{\large \frac{1}{\sqrt{3}}}\)
\(\sin{\theta}={\large \frac{3}{\sqrt{10}}}~,~\cos{\theta}={\large \frac{1}{\sqrt{10}}}\)
または
\(\sin{\theta}=-{\large \frac{3}{\sqrt{10}}}~,~\cos{\theta}=-{\large \frac{1}{\sqrt{10}}}\)
\({\small (1)}~\)[証明]
(左辺)
\(=\sin^2{\theta}(1-\sin^2{\theta})\)
\(=(1-\cos^2{\theta})\cos^2{\theta}\)
\(=\cos^2{\theta}-\cos^4{\theta}\)
したがって、
\(\sin^2{\theta}-\sin^4{\theta}\)
\(=\cos^2{\theta}-\cos^4{\theta}\)
[終]
\({\small (2)}~\)[証明]
(左辺)$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}-\sin^2{\theta}$$$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}-\frac{\sin^2{\theta}\cos^2{\theta}}{\cos^2{\theta}}$$$$=\frac{\sin^2{\theta}(1-\cos^2{\theta})}{\cos^2{\theta}}$$$$=\frac{\sin^4{\theta}}{\cos^2{\theta}}$$$$=\tan^2{\theta}\sin^2{\theta}$$したがって、$$\tan^2{\theta}-\sin^2{\theta}=\tan^2{\theta}\sin^2{\theta}$$[終]
\({\small (3)}~\)[証明]
(左辺)$$=\frac{1}{\sin{\theta}}\cdot\frac{\sin{\theta}}{\cos{\theta}}-\sin{\theta}\cdot\frac{\cos{\theta}}{\sin{\theta}}$$$$=\frac{1}{\cos{\theta}}-\cos{\theta}$$$$=\frac{1-\cos^2{\theta}}{\cos{\theta}}$$$$=\frac{\sin^2{\theta}}{\cos{\theta}}$$$$=\sin{\theta}\tan{\theta}$$したがって、$$\frac{\tan{\theta}}{\sin{\theta}}-\frac{\sin{\theta}}{\tan{\theta}}=\sin{\theta}\tan{\theta}$$[終]
\({\small (1)}~\)
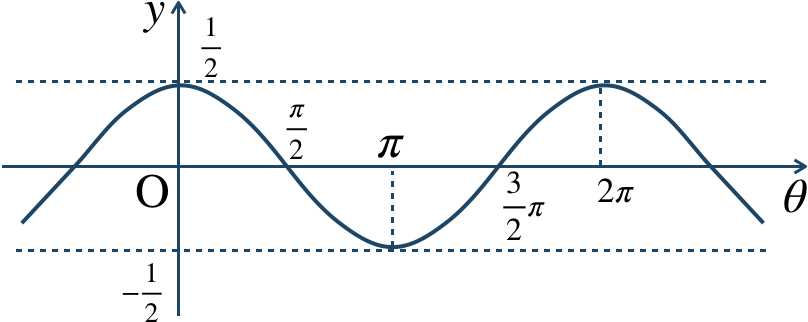
周期 \(2\pi\)
\({\small (2)}~\)
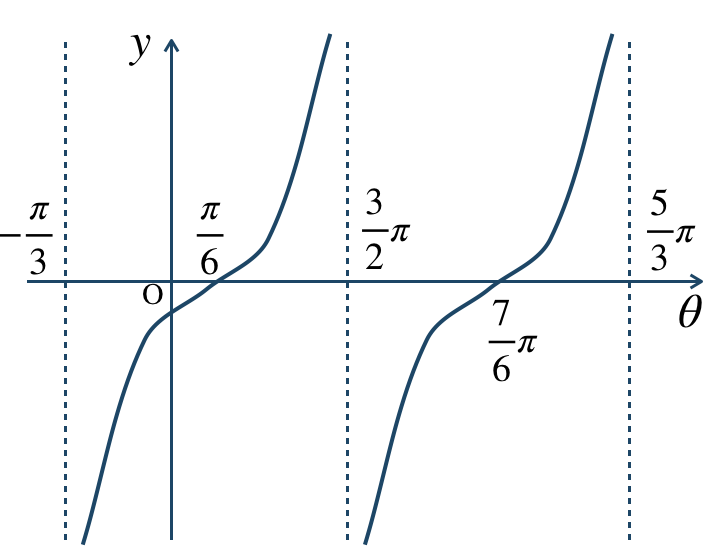
周期 \(\pi\)
\({\small (3)}~\)
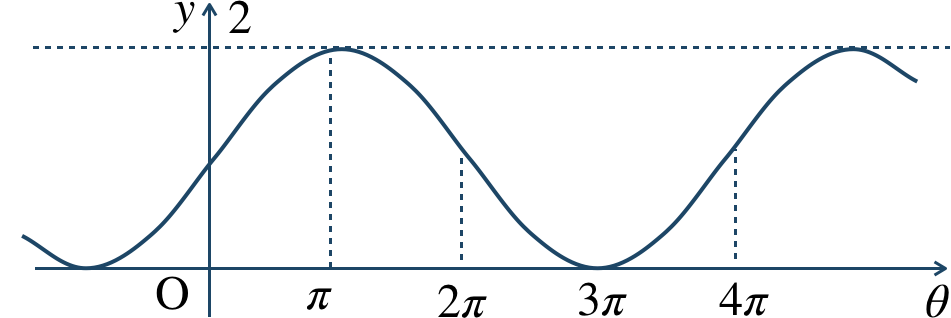
周期 \(4\pi\)
\({\small (4)}~\)
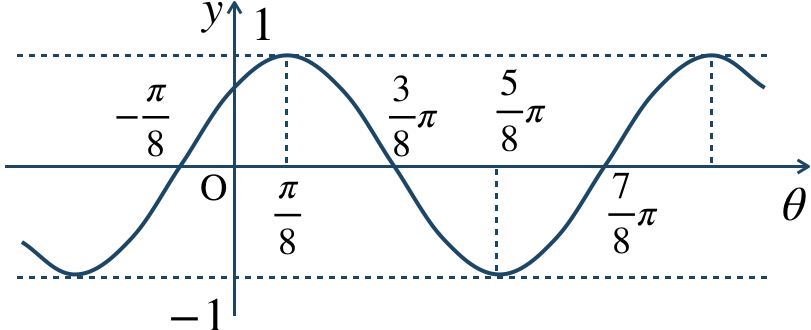
周期 \(\pi\)
\({\small (5)}~\)
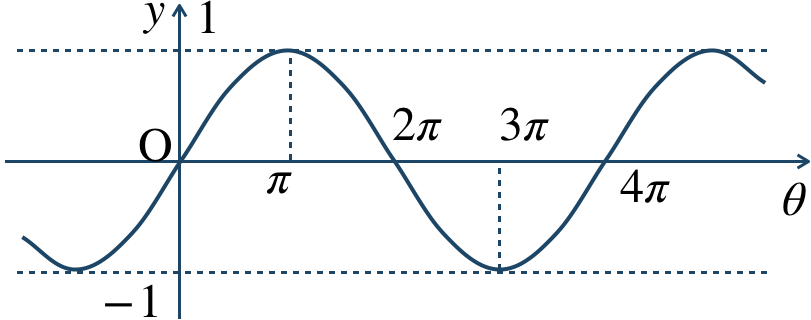
周期 \(4\pi\)
\({\small (1)}~\theta={\large \frac{3}{4}}\pi~,~{\large \frac{5}{4}}\pi\)
\({\small (2)}~\theta={\large \frac{5}{6}}\pi~,~{\large \frac{11}{6}}\pi\)
\({\small (3)}~0≦\theta≦{\large \frac{\pi}{3}}~,~{\large \frac{2}{3}}\pi≦\theta<2\pi\)
\({\small (4)}~{\large \frac{\pi}{2}}<\theta≦{\large \frac{2}{3}}\pi~,~{\large \frac{3}{2}}\pi<\theta≦{\large \frac{5}{3}}\pi\)
\({\small (5)}~\theta={\large \frac{\pi}{6}}~,~{\large \frac{3}{2}}\pi\)
\({\small (6)}~0≦\theta<{\large \frac{7}{12}}\pi~,~{\large \frac{11}{12}}\pi<\theta<2\pi\)
\({\small (1)}~\)
\(\theta=0~,~\pi\) で最大値 \(-2\)
\(\theta={\large \frac{\pi}{2}}\) で最小値 \(-3\)
\({\small (2)}~\)
\(\theta={\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi\) で最大値 \({\large \frac{5}{4}}\)
\(\theta={\large \frac{3}{2}}\pi\) で最小値 \(-1\)
\({\small (3)}~\)
最大値なし
\(\theta=-{\large \frac{\pi}{4}}\) で最小値 \(2\)
第2節 加法定理
\({\small (1)}~{\large \frac{\sqrt{6}-\sqrt{2}}{4}}\) \({\small (2)}~{\large \frac{\sqrt{6}-\sqrt{2}}{4}}\)
\({\small (3)}~{\large \frac{\sqrt{6}+\sqrt{2}}{4}}\) \({\small (4)}~{\large \frac{\sqrt{6}-\sqrt{2}}{4}}\)
\(\sin{{\large \frac{7}{12}}\pi}={\large \frac{\sqrt{6}+\sqrt{2}}{4}}\)
\(\cos{{\large \frac{7}{12}}\pi}={\large \frac{\sqrt{2}-\sqrt{6}}{4}}\)
→ 加法定理
\({\small (1)}~-{\large \frac{6+4\sqrt{5}}{15}}\) \({\small (2)}~-{\large \frac{3\sqrt{5}+8}{15}}\)
→ 加法定理と式の値
\({\small (1)}~2-\sqrt{3}\) \({\small (2)}~-2-\sqrt{3}\)
\({\small (3)}~-2+\sqrt{3}\)
\({\small (1)}~{\large \frac{\pi}{3}}\) \({\small (2)}~{\large \frac{\pi}{4}}\)
→ 2直線のなす角
\(\left({\large \frac{1}{\sqrt{2}}}~,~{\large \frac{5}{\sqrt{2}}}\right)\)
\({\small (1)}~-{\large \frac{4\sqrt{5}}{9}}\) \({\small (2)}~-{\large \frac{1}{9}}\)
\({\small (3)}~4\sqrt{5}\)
→ 2倍角の公式
\({\small (1)}~\) [証明]
\(~~~~~\sin{3\alpha}\)
\(=\sin{(2\alpha+\alpha)}\)
\(=\sin{2\alpha}\cos{\alpha}+\cos{2\alpha}\sin{\alpha}\)
\(=2\sin{\alpha}\cos^2{\alpha}+(1-2\sin^2{\alpha})\sin{\alpha}\)
\(=2\sin{\alpha}(1-\sin^2{\alpha})+\sin{\alpha}-2\sin^3{\alpha}\)
\(=3\sin{\alpha}-4\sin^3{\alpha}\)
したがって、
\(\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}\) [終]
\({\small (2)}~\) [証明]
\(~~~~~\cos{3\alpha}\)
\(=\cos{(2\alpha+\alpha)}\)
\(=\cos{2\alpha}\cos{\alpha}-\sin{2\alpha}\sin{\alpha}\)
\(=(2\cos^2{\alpha}-1)\cos{\alpha}-2\sin^2{\alpha}\cos{\alpha}\)
\(=2\cos^3{\alpha}-\cos{\alpha}-2(1-\cos^2{\alpha})\cos{\alpha}\)
\(=4\cos^3{\alpha}-3\cos{\alpha}\)
したがって、
\(\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}\) [終]
\({\small (1)}~\)[証明]
(左辺)
\(=\sin^2{\theta}+2\sin{\theta}\cos{\theta}+\cos^2{\theta}\)
\(=1+2\sin{\theta}\cos{\theta}\)
(右辺)
\(=1+2\sin{\theta}\cos{\theta}\)
したがって、
\((\sin{\theta}+\cos{\theta})^2=1+\sin{2\theta}\)
[終]
\({\small (2)}~\)[証明]
(左辺)
\(=(\cos^2{\theta}+\sin^2{\theta})(\cos^2{\theta}-\sin^2{\theta})\)
\(=\cos^2{\theta}-\sin^2{\theta}\)
(右辺)
\(=\cos^2{\theta}-\sin^2{\theta}\)
したがって、
\(\cos^4{\theta}-\sin^4{\theta}=\cos{2\theta}\)
[終]
\({\small (1)}~{\large \frac{\sqrt{2+\sqrt{2}}}{2}}\) \({\small (2)}~\sqrt{2}-1\)
\({\small (1)}~{\large \frac{3}{\sqrt{10}}}\) \({\small (2)}~{\large \frac{1}{\sqrt{10}}}\)
\({\small (3)}~3\)
→ 半角の公式
\({\small (1)}~x={\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi\)
\({\small (2)}~x=0~,~{\large \frac{\pi}{3}}~,~\pi~,~{\large \frac{5}{3}}\pi\)
\({\small (3)}~{\large \frac{\pi}{6}}≦x≦{\large \frac{5}{6}}\pi\)
\({\small (4)}~0<x<{\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi<x<2\pi\)
→ 2倍角を含む方程式・不等式
\({\small (1)}~{\large \frac{1}{2}}(\sin{6\theta}+\sin{2\theta})\)
\({\small (2)}~{\large \frac{1}{2}}(\cos{4\theta}+\cos{2\theta})\)
\({\small (3)}~-{\large \frac{1}{2}}(\cos{4\theta}-\cos{2\theta})\)
\({\small (1)}~2\sin{4\theta}\cos{\theta}\)
\({\small (2)}~2\cos{2\theta}\cos{\theta}\)
\({\small (3)}~2\sin{4\theta}\sin{\theta}\)
\({\small (1)}~{\large \frac{\sqrt{3}+1}{4}}\) \({\small (2)}~{\large \frac{\sqrt{3}-1}{4}}\)
\({\small (3)}~{\large \frac{1}{4}}\) \({\small (4)}~{\large \frac{1}{\sqrt{2}}}\)
\({\small (5)}~{\large \frac{\sqrt{6}}{2}}\) \({\small (6)}~-{\large \frac{1}{\sqrt{2}}}\)
\(x=0~,~{\large \frac{\pi}{2}}~,~\pi~,~{\large \frac{3}{2}}\pi\)
\({\small (1)}~2\sin{\left(\theta+{\large \frac{\pi}{6}}\right)}\)
\({\small (2)}~\sqrt{2}\sin{\left(\theta-{\large \frac{\pi}{4}}\right)}\)
→ 三角関数の合成
\({\small (1)}~x=\pi~,~{\large \frac{3}{2}}\pi\)
\({\small (2)}~x={\large \frac{\pi}{2}}~,~{\large \frac{5}{6}}\pi\)
\({\large \frac{\pi}{2}}<x<{\large \frac{7}{6}}\pi\)
\({\small (1)}~{\large \frac{\pi}{2}}<x<{\large \frac{11}{6}}\pi\)
\({\small (2)}~0≦x≦{\large \frac{5}{12}}\pi~,~{\large \frac{11}{12}}\pi≦x<2\pi\)
→ 合成を用いる方程式と不等式
\(x={\large \frac{2}{3}}\pi\) のとき最大値 \(2\)
\(x={\large \frac{5}{3}}\pi\) のとき最大値 \(-2\)
最大値 \(\sqrt{5}\)、最小値 \(-\sqrt{5}\)
問題
\({\small (1)}~{\large \frac{\sqrt{6}}{2}}\) \({\small (2)}~{\large \frac{\sqrt{6}}{2}}\) \({\small (3)}~{\large \frac{\sqrt{6}}{2}}\)
\({\small (1)}~\)[証明]$$~~~~~\sin{(\alpha+\beta)}\sin{(\alpha-\beta)}$$$$~=(\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta})$$$$~~~~~~(\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta})$$$$=\sin^2{\alpha}\cos^2{\beta}-\cos^2{\alpha}\sin^2{\beta}$$$$=\sin^2{\alpha}(1-\sin^2{\beta})$$$$~~~~~~-(1-\sin^2{\alpha})\sin^2{\beta}$$$$=\sin^2{\alpha}-\sin^2{\beta}$$次に、$$~~~~~\sin^2{\alpha}-\sin^2{\beta}$$$$=(1-\cos^2{\alpha})-(1-\cos^2{\beta})$$$$=\cos^2{\beta}-\cos^2{\alpha}$$したがって、$$~~\sin{(\alpha+\beta)}\sin{(\alpha-\beta)}$$$$~~~~~=\sin^2{\alpha}-\sin^2{\beta}$$$$~~~~~~~=\cos^2{\beta}-\cos^2{\alpha}$$[終]
\({\small (2)}~\)[証明]
(右辺)$$~=\frac{\sin{(\alpha-\beta)}}{\sin{(\alpha-\beta)}}$$$$~=\frac{\sin{\alpha}\cos{\beta}-\cos{\beta}\sin{\alpha}}{\sin{\alpha}\cos{\beta}+\cos{\beta}\sin{\alpha}}$$分母分子を \(\cos{\alpha}\cos{\beta}\) で割ると、$$~=\frac{{\large \frac{\sin{\alpha}}{\cos{\alpha}}}-{\large \frac{\sin{\beta}}{\cos{\beta}}}}{{\large \frac{\sin{\alpha}}{\cos{\alpha}}}+{\large \frac{\sin{\beta}}{\cos{\beta}}}}$$$$~=\frac{\tan{\alpha}-\tan{\beta}}{\tan{\alpha}+\tan{\beta}}$$したがって、$$~\frac{\tan{\alpha}-\tan{\beta}}{\tan{\alpha}+\tan{\beta}}$$$$~~~=\frac{\sin{(\alpha-\beta)}}{\sin{(\alpha-\beta)}}$$[終]
\({\small (1)}~-{\large \frac{6}{7}}\) \({\small (2)}~1\)
\(y=(\sqrt{3}+2)x~,~y=(\sqrt{3}-2)x\)
\({\small (1)}~-{\large \frac{7}{25}}\) \({\small (2)}~{\large \frac{24}{25}}\) \({\small (3)}~{\large \frac{2}{\sqrt{5}}}\)
\({\small (1)}~x={\large \frac{\pi}{2}}~,~{\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi~,~{\large \frac{3}{2}}\pi\)
\({\small (2)}~x={\large \frac{\pi}{3}}~,~{\large \frac{\pi}{2}}~,~{\large \frac{2}{3}}\pi~,~{\large \frac{3}{2}}\pi\)
\({\small (3)}~x={\large \frac{5}{6}}\pi~,~{\large \frac{11}{6}}\pi\)
\({\small (4)}~x={\large \frac{\pi}{4}}~,~{\large \frac{\pi}{2}}~,~{\large \frac{5}{4}}\pi~,~{\large \frac{3}{2}}\pi\)
\({\small (5)}~0≦x≦{\large \frac{2}{3}}\pi~,~{\large \frac{5}{3}}\pi≦x<2\pi\)
\({\small (6)}~{\large \frac{\pi}{12}}<x<{\large \frac{17}{12}}\pi\)
\(x={\large \frac{7}{6}}\pi~,~{\large \frac{11}{6}}\pi\) のとき最大値 \({\large \frac{5}{2}}\)
\(x={\large \frac{\pi}{2}}\) のとき最大値 \(-2\)
演習問題 三角関数
演習問題A
\({\small (1)}~{\large \frac{7}{18}}\) \({\small (2)}~{\large \frac{4}{3}}\)
\({\small (3)}~\)
\(\sin{\theta}={\large \frac{4+\sqrt{2}}{6}}~,~\cos{\theta}={\large \frac{4-\sqrt{2}}{6}}\)
\({\small (1)}~x=0~,~{\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi\)
\({\small (2)}~0≦x≦{\large \frac{\pi}{6}}~,~{\large \frac{\pi}{2}}≦x≦{\large \frac{2}{3}}\pi\)
\({\small (1)}~\)
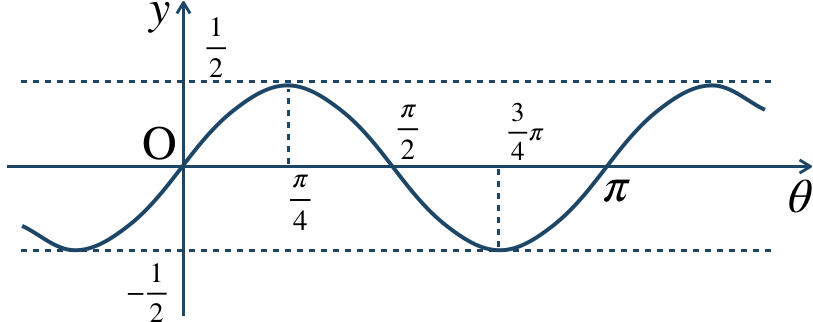
周期 \(\pi\)
\({\small (2)}~\)
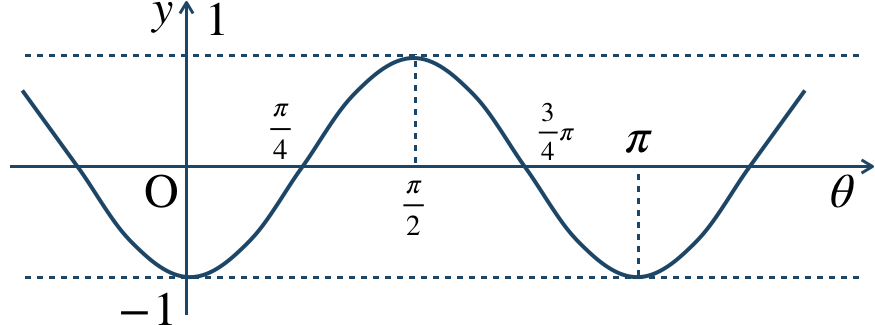
周期 \(\pi\)
\({\small (3)}~\)
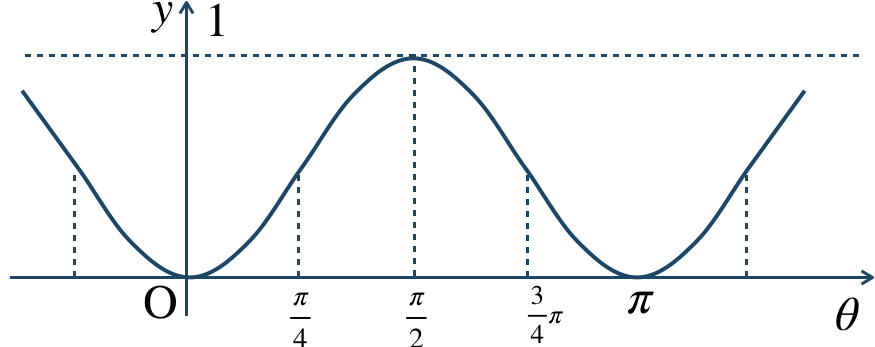
周期 \(\pi\)
演習問題B
\(\sin{(\alpha+\beta)}<\sin{\alpha}+\sin{\beta}\)
\(-{\large \frac{59}{72}}\)
\({\small (1)}~\)[証明]
\(t=\tan{{\large \frac{\theta}{2}}}\) であることより、$$~~~1+t^2=\frac{1}{\cos{{\large \frac{\theta}{2}}}}$$$$~\Leftrightarrow~\frac{1}{1+t^2}=\cos^2{\frac{\theta}{2}}$$これより、
(右辺)$$=\left(1-\tan^2{\frac{\theta}{2}}\right)\cos^2{\frac{\theta}{2}}$$$$=\left(1-\frac{\sin^2{{\large \frac{\theta}{2}}}}{\cos^2{{\large \frac{\theta}{2}}}}\right)\cos^2{\frac{\theta}{2}}$$$$=\cos^2{\frac{\theta}{2}}-\sin^2{\frac{\theta}{2}}$$\(\cos{\theta}\) の2倍角の公式より、$$=\cos{\theta}$$したがって、$$~~~\cos{\theta}=\frac{1-t^2}{1+t^2}$$[終]
\({\small (2)}~\)[証明]
(右辺)$$=\frac{2\tan{{\large \frac{\theta}{2}}}}{1-\tan^2{{\large \frac{\theta}{2}}}}$$\(\tan{\theta}\) の2倍角の公式より、$$=\tan{\theta}$$したがって、$$~~~\tan{\theta}=\frac{2t}{1-t^2}$$[終]
\({\small (3)}~\)[証明]
(右辺)$$=2\tan{\frac{\theta}{2}}\cos^2{\frac{\theta}{2}}$$$$=2\cdot \frac{\sin{{\large \frac{\theta}{2}}}}{\cos{{\large \frac{\theta}{2}}}}\cdot \cos^2{\frac{\theta}{2}}$$$$=2\sin{\frac{\theta}{2}}\cos{\frac{\theta}{2}}$$\(\sin{\theta}\) の2倍角の公式より、$$=\sin{\theta}$$したがって、$$~~~\sin{\theta}=\frac{2t}{1+t^2}$$[終]
\(x={\large \frac{\pi}{8}}~,~{\large \frac{9}{8}}\pi\) のとき最大値 \(2\sqrt{2}+3\)
\(x={\large \frac{5}{8}}\pi~,~{\large \frac{13}{8}}\pi\) のとき最大値 \(-2\sqrt{2}+3\)
\({\small (1)}~y=t^2+t-1\)
\({\small (2)}~-\sqrt{2}≦t≦\sqrt{2}\)
\({\small (3)}~\)最大値 \(1+\sqrt{2}\)
最小値 \(-{\large \frac{5}{4}}\)
次のページ「第5章 指数関数と対数関数」