文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第4章 三角関数
第5章 指数関数と対数関数
第6章 微分法と積分法
第1節 微分係数と導関数
練習1
\(19.6\) m/s
発展1
\({\small (1)}~1\) \({\small (2)}~3\)
発展2
\({\small (1)}~-6\) \({\small (2)}~0\)
発展3
\({\small (1)}~-4\) \({\small (2)}~{\large \frac{1}{2}}\) \({\small (3)}~{\large \frac{1}{2}}\)
練習6
\({\small (1)}~y’=2x-2\)
\({\small (2)}~y’=-6x-5\)
\({\small (3)}~y’=9x^2-4x+4\)
\({\small (4)}~y’=-6x^2+5\)
\({\small (5)}~y’=4x^3-9x^2+4\)
\({\small (6)}~y’=4x^2-{\large \frac{1}{3}}x+{\large \frac{2}{3}}\)
\({\small (7)}~y’=12x+7\)
\({\small (8)}~y’=6x^2+6x+3\)
→ 微分の計算
練習7
\({\small (1)}~0\) \({\small (2)}~1\) \({\small (3)}~-39\)
練習9
\({\large \frac{dS}{da}}=12a\)
問題
1
\({\small (1)}~y’=6x^2-4\)
\({\small (2)}~y’=-2x^3-2x^2+x-1\)
\({\small (3)}~y’=3x^2-6x-1\)
\({\small (4)}~y’=-3x^2+18x-27\)
\({\small (5)}~y’=3x^2\)
\({\small (6)}~y’=24x^2\)
2
\({\small (1)}~a+b-1\)
\({\small (2)}~\)[証明] \(f(x)\) を微分すると、
\(f'(x)=2x-1\)
\(x=c\) での微分係数は、
\(f'(c)=2c-1\)
これと(1)の答えより、
\(2c-1=a+b-1\)
したがって、
\(c={\large \frac{a+b}{2}}\) [終]
3
\({\small (1)}~\)[証明] \(y=a^2x^2+2abx+b^2\) より、微分すると、
\(y’=2a^2x+2ab=2a(ax+b)\)
したがって、
\(y=(ax+b)^2\) のとき \(y’=2a(ax+b)\) [終]
\({\small (2)}~\)[証明]
\(y=a^3x^3+3a^2bx^2+3ab^2x+b^3\) より、微分すると、
\(y’=3a^3x^2+6a^2bx+3a^2\)
\(~~=3a(a^2x^2+2abx+b^2)\)
\(~~=3a(ax+b)^2\)
したがって、
\(y=(ax+b)^3\) のとき \(y’=3a(ax+b)^2\) [終]
4
\(p^2-3q≧0\)
5
\({\large \frac{dh}{dt}}=v_0-gt\)
6
\(3\pi\)
第2節 導関数の応用
練習11
\({\small (1)}~\)
\(y=-x-1~,~(1,-2)\)
または
\(y=7x-25~,~(5,10)\)
\({\small (2)}~\)
\(y=3x-2~,~(1,1)\)
→ 接線の方程式②(外部の点から引いた接線)
問1
[証明] \(f(x)=x^3+2x\) の導関数は、
\(f'(x)=3x^2+2\)
これは任意の \(x\) に対して \(f'(x)>0\)
したがって、関数 \(f(x)=x^3+2x\) は常に単調に増加する [終]
練習12
\({\small (1)}~\)
\(x≦-3\) で増加
\(-3≦x≦-1\) で減少
\(-1≦x\) で増加
\({\small (2)}~\)
\(x≦-1\) で減少
\(-1≦x≦1\) で増加
\(1≦x\) で減少
\({\small (3)}~\)常に減少
練習13
\({\small (1)}~\)
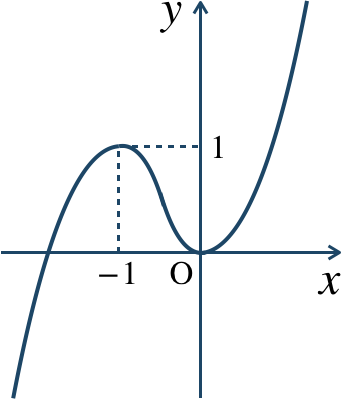
\(x=-1\) で極大値 \(1\)
\(x=0\) で極小値 \(0\)
\({\small (2)}~\)
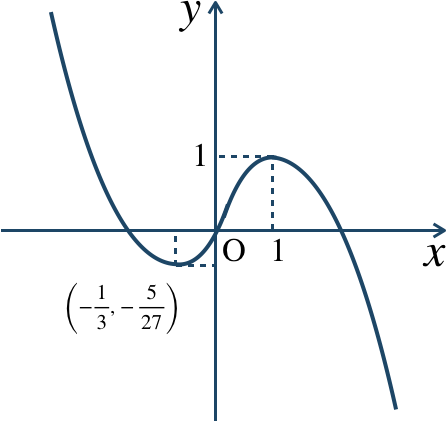
\(x=1\) で極大値 \(1\)
\(x=-{\large \frac{1}{3}}\) で極小値 \(-{\large \frac{5}{27}}\)
→ 3次関数のグラフと増減表
練習14
\({\small (1)}~\)
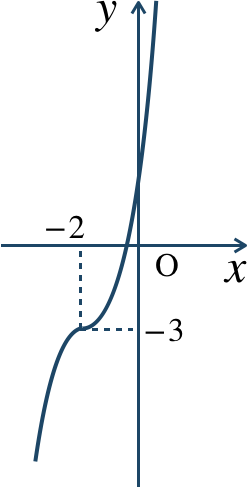
\({\small (2)}~\)
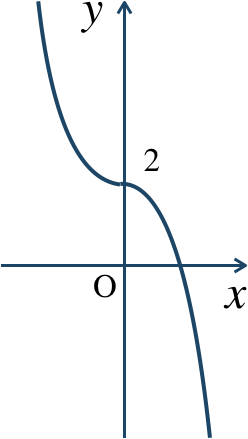
練習15
\({\small (1)}~\)
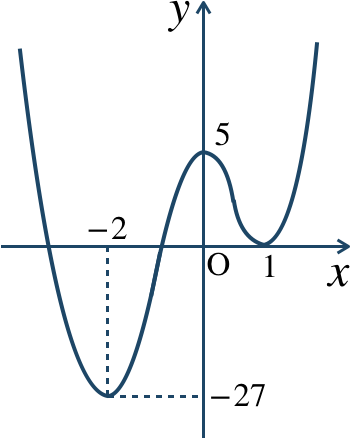
\(x=-2\) で極小値 \(-27\)
\(x=0\) で極大値 \(5\)
\(x=1\) で極小値 \(0\)
\({\small (2)}~\)
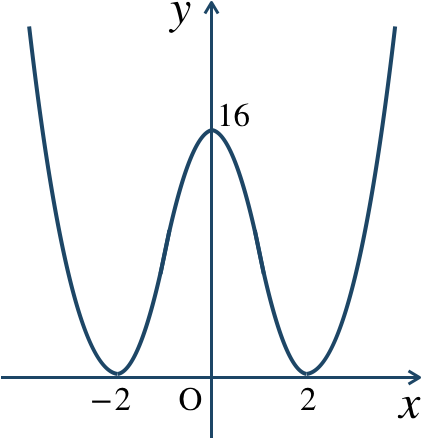
\(x=0\) で極大値 \(16\)
\(x=\pm2\) で極小値 \(0\)
\({\small (3)}~\)
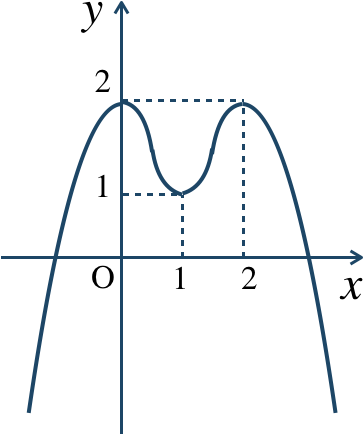
\(x=0\) で極大値 \(2\)
\(x=1\) で極小値 \(1\)
\(x=2\) で極大値 \(2\)
\({\small (4)}~\)
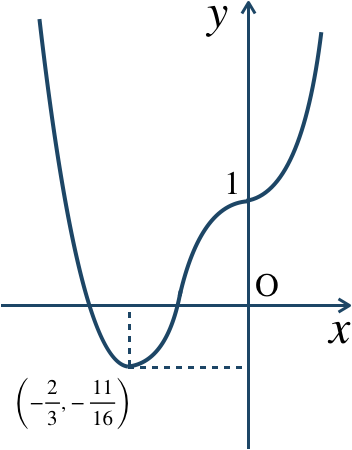
\(x=-{\large \frac{3}{2}}\) で極小値 \(-{\large \frac{11}{16}}\)
→ 4次関数のグラフと増減表
練習17
\({\small (1)}~\)
\(x=3\) で最大値 \(22\)
\(x=-2~,~1\) で最小値 \(2\)
\({\small (2)}~\)
\(x=2\) で最大値 \(0\)
\(x=3\) で最小値 \(-8\)
\({\small (3)}~\)
\(x=-1\) で最大値 \(17\)
\(x=3\) で最小値 \(-15\)
→ 3次関数の最大値・最小値
練習18
\(6\) ㎝
練習21
\({\small (1)}~\)1個 \({\small (2)}~\)3個
\({\small (3)}~\)2個 \({\small (4)}~\)2個
→ 3次方程式の解の個数①
問2
\({\small (1)}~a=0~,~4\)
\({\small (2)}~a<0~,~4<a\)
練習20
\({\small (1)}~\)
\(a<-1~,~0<a\) のとき1個
\(a=-1~,~0\) のとき2個
\(-1<a<0\) のとき3個
\({\small (2)}~\)
\(a<2~,~a=3\) のとき2個
\(a=2\) のとき3個
\(2<a<3\) のとき4個
\(a>3\) のとき0個
→ 3次方程式の解の個数②(定数分離法)
練習21
[証明] \(f(x)=2x^3-9x^2+12x-4\) とすると、
\(f'(x)=6x^2-18x+12\)
\(=6(x-1)(x-2)\)
よって、\(x≧1\) での増減表は
| \(x\) | \(1\) | \(\cdots\) | \(2\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | |
| \(f(x)\) | \(1\) | ↘︎ | \(0\) | ↗︎ |
よって、\(x≧1\) で最小値が \(0\) であるので、
\(f(x)≧0\)
したがって、\(x≧1\) のとき
\(2x^3-9x^2+12x-4≧0\) [終]
→ 3次不等式の証明
練習22
[証明] \(f(x)=x^4-4x+3\) とすると、
\(f'(x)=4x^3-4\)
\(=4(x-1)(x^2+x+1)\)
ここで、\(f'(x)=0\) となるのは \(x=1\)
増減表は、
| \(x\) | \(\cdots\) | \(1\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | ↘︎ | \(0\) | ↗︎ |
最小値が \(0\) であるので、\(f(x)≧0\)
したがって、
\(x^4+3≧4x\) [終]
問題
7
\({\small (1)}~a=-1~,~b=2\)
\({\small (2)}~a=1~,~b=0\)
8
\(-3≦a≦3\)
9
\({\small (1)}~\)
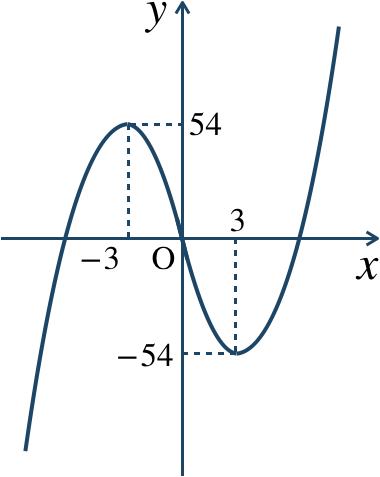
\(x≦-3\) で増加
\(-3≦x≦3\) で減少
\(3≦x\) で増加
\(x=-3\) で極大値 \(54\)
\(x=3\) で極小値 \(-54\)
\({\small (2)}~\)
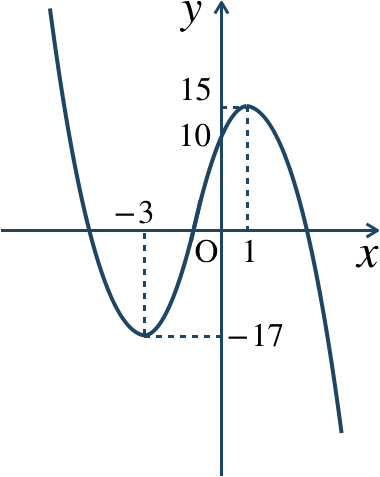
\(x≦-3\) で減少
\(-3≦x≦1\) で増加
\(1≦x\) で減少
\(x=1\) で極大値 \(15\)
\(x=-3\) で極小値 \(-17\)
\({\small (3)}~\)

常に単調に減少
極値なし
\({\small (4)}~\)
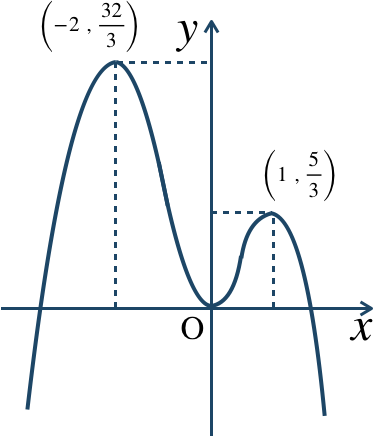
\(x≦-2\) で増加
\(-2≦x≦0\) で減少
\(0≦x≦1\) で増加
\(1≦x\) で減少
\(x=-2\) で極大値 \({\large \frac{32}{3}}\)
\(x=0\) で極小値 \(0\)
\(x=1\) で極大値 \({\large \frac{5}{3}}\)
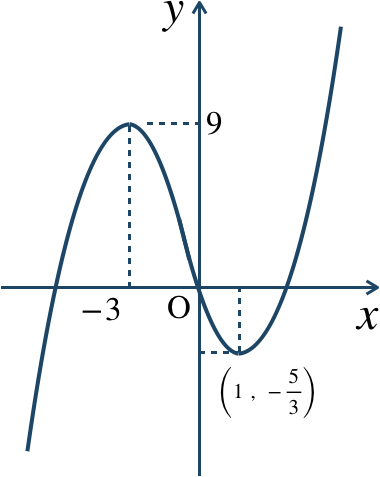
10
\(f(x)=-x^3+3x^2\)
11
\({\small (1)}~\)
\(x=2\) で最大値 \(20a+b\)
\(x=0\) で最小値 \(b\)
\({\small (2)}~a={\large \frac{9}{10}}~,~b=-8\)
12
半径 \({\large \frac{2}{3}}r\)、高さ \({\large \frac{h}{3}}\)
13
\(0<a<4\sqrt{2}\)
14
[証明] \(f(x)=x^4+4x^3+28\) とすると、
\(f'(x)=4x^3+12x^2\)
\(=4x^2(x+3)\)
ここで、\(f'(x)=0\) となるのは \(x=-3~,~0\)
増減表は、
| \(x\) | \(\cdots\) | \(-3\) | \(\cdots\) | \(0\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | \(0\) | \(+\) |
| \(f(x)\) | ↘︎ | \(1\) | ↗︎ | \(28\) | ↗︎ |
よって、\(x=-3\) で最小値が \(1\) であるので、\(f(x)>0\)
したがって、
\(x^4+4x^3+28>0\) [終]
第3節 積分法
練習23
\(C\) を積分定数として、
\({\small (1)}~2x^3+C\)
\({\small (2)}~{\large \frac{1}{2}}x^4+C\)
\({\small (3)}~x^2+3x+C\)
\({\small (4)}~3x^3-x^2-x+C\)
\({\small (5)}~-x^4-{\large \frac{2}{3}}x^3+x+C\)
練習24
\(C\) を積分定数として、
\({\small (1)}~2x^3+{\large \frac{1}{2}}x^2-x+C\)
\({\small (2)}~-{\large \frac{1}{4}}x^4+x^3+C\)
\({\small (3)}~3t^3-t+C\)
\({\small (4)}~{\large \frac{4}{3}}t^3-2t^2+t+C\)
→ 不定積分
練習26
\(y=x^2-4x+5\)
練習28
[証明] \(a>-1\) として、4点が
\({\rm A}(a,0)~,~{\rm B}(a,a+1)\)
\({\rm P}(x,0)~,~{\rm Q}(x,x+1)\)
となるので、
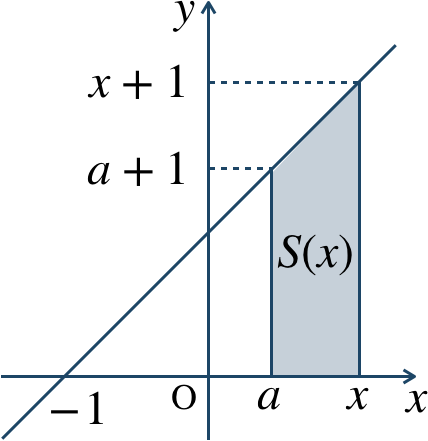
図の台形 \({\rm ABQP}\) の面積 \(S(x)\) は、$$~S(x)=\frac{1}{2}\{(a+1)+(x+1)\}(x-a)$$$$~~~=\frac{1}{2}(x^2+2x-a^2-2a)$$これを微分すると、$$~S'(x)=x+1$$したがって、\(S'(x)=f(x)\) が成り立つ [終]
問3
[証明] 性質2
\(f(x)~,~g(x)\) の原始関数の1つをそれぞれ \(F(x)~,~G(x)\) とすると、
\(\int \{f(x)+g(x)\}dx\)
\(~=\int f(x)dx+\int g(x)dx\)
\(~=F(x)+G(x)\)
よって、
\(\int_{a}^{b}\{f(x)+g(x)\}dx\)
\(~=\left[ F(x)+G(x) \right]_{a}^{b}\)
\(~=\{F(b)+G(b)\}-\{F(a)+G(a)\}\)
\(~=F(b)-F(a)+G(b)-G(a)\)
\(~=\int_{a}^{b}f(x)dx+\int_{a}^{b}g(x)dx\)
[終]
[証明] 性質3
性質1より、
\(k\int_{a}^{b}f(x)dx=\int_{a}^{b}kf(x)dx\)
\(l\int_{a}^{b}g(x)dx=\int_{a}^{b}lg(x)dx\)
性質2より、
\(k\int_{a}^{b}f(x)dx+l\int_{a}^{b}g(x)dx\)
\(~=\int_{a}^{b}kf(x)dx+\int_{a}^{b}lg(x)dx\)
\(~=\int_{a}^{b}\{kf(x)+lg(x)\}dx\)
[終]
練習30
\({\small (1)}~50\) \({\small (2)}~{\large \frac{3}{4}}\)
問4
[証明] 性質4
\(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{a}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{a}^{a}\)
\(=F(a)-F(a)=0\)
したがって、
\(\int_{a}^{a}f(x)dx=0\) [終]
[証明] 性質5
\(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{b}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{b}^{a}\)
\(=F(a)-F(b)\)
\(=-\left(F(b)-F(a)\right)\)
\(=-\left[ F(x) \right]_{a}^{b}\)
\(=-\int_{a}^{b}f(x)dx\)
したがって、
\(\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx\) [終]
[証明] 性質6
\(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx\)
\(=\left[ F(x) \right]_{a}^{c}+\left[ F(x) \right]_{c}^{b}\)
\(=F(c)-F(a)+F(b)-F(c)\)
\(=F(b)-F(a)\)
\(=\int_{a}^{b}f(x)dx\)
したがって、
\(\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx\)
\(=\int_{a}^{b}f(x)dx\) [終]
練習31
\({\small (1)}~{\large \frac{7}{3}}\) \({\small (2)}~-1\) \({\small (3)}~-{\large \frac{3}{2}}\)
→ 定積分の計算
問5
\(g'(x)=3x^2-x\)
練習34
\({\small (1)}~6\) \({\small (2)}~{\large \frac{32}{3}}\) \({\small (2)}~{\large \frac{27}{4}}\)
→ 定積分と面積①(x軸と囲まれた面積)
練習35
\({\small (1)}~{\large \frac{32}{3}}\) \({\small (2)}~{\large \frac{8}{3}}\)
→ 定積分と面積②(2つの関数で囲まれた面積)
練習36
\({\large \frac{125}{6}}\)
練習37
\({\large \frac{64}{3}}\)
練習38
\({\large \frac{1}{2}}\)
練習41
\({\large \frac{64}{3}}\)
研究1
\(y’=4(x-2)^3\)
研究2
\({\large \frac{65}{4}}\)
研究3
\(-{\large \frac{625}{12}}\)
研究4
[証明]
(左辺)
\(=\int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)dx\)
\(=\int_{\alpha}^{\beta}(x-\alpha)^2\{(x-\alpha)-(\beta-\alpha)\}dx\)
\(=\int_{\alpha}^{\beta}(x-\alpha)^3dx\)
\(-(\beta-\alpha)\int_{\alpha}^{\beta}(x-\alpha)^2dx\)
\(={\Large [} {\large \frac{1}{4}}(x-\alpha)^4 {\Large ]}_{\alpha}^{\beta}\)
\(-(\beta-\alpha){\Large [} {\large \frac{1}{3}}(x-\alpha)^3 {\Large ]}_{\alpha}^{\beta}\)
\(={\large \frac{1}{4}}(\beta-\alpha)^4\)
\(-(\beta-\alpha)\cdot{\large \frac{1}{3}}(\beta-\alpha)^3\)
\(=-{\large \frac{1}{12}}(\beta-\alpha)^4\) [終]
問題
15
\({\small (1)}~{\large \frac{23}{6}}\) \({\small (2)}~-{\large \frac{9}{2}}\)
\({\small (3)}~-{\large \frac{65}{4}}\) \({\small (4)}~-{\large \frac{64}{3}}\)
\({\small (5)}~5\) \({\small (6)}~3\)
16
\({\small (1)}~a=15b\)
\({\small (2)}~\)[証明]
\(g(x)\) を \(g(x)=px+q\) とする
(1)より、\(f(x)=15bx+b\)
条件式より、$$~~~~~~\int_{-1}^{1}f(x)g(x)dx$$$$~=\int_{-1}^{1}(15bx+b)(px+q)dx$$$$~=b\int_{-1}^{1}\{15px^2+(p+15q)x+q\}dx$$$$~=b{\Large [} 5px^3+\frac{p+15q}{2}x^2+qx {\Large ]}_{-1}^{1}$$$$~=2b(5p+q)$$よって、\(2b(5p+q)=0\) となり \(b\) は任意の値より、
\(5p+q=0~\Leftrightarrow~q=-5p\)
したがって、
\(g(x)=px-5p=p(x-5)\) [終]
17
18
\({\small (1)}~{\large \frac{9}{2}}\) \({\small (2)}~{\large \frac{71}{3}}\) \({\small (3)}~{\large \frac{4}{3}}\)
19
[証明] この放物線と直線の交点の \(x\) 座標は、
\(x(x-1)=(\sqrt[\large 3]{2}-1)x\)
\(~\Leftrightarrow~x(x-\sqrt[\large 3]{2})=0\)
よって、\(x=0~,~\sqrt[\large 3]{2}\)
放物線と直線で囲まれた面積は、$$~~~~~~\int_{0}^{\sqrt[\large 3]{2}}\{(\sqrt[\large 3]{2}-1)x-x(x-1)\}dx$$$$~=\int_{0}^{\sqrt[\large 3]{2}}(\sqrt[\large 3]{2}x-x^2)dx$$$$~={\Large [} \frac{\sqrt[\large 3]{2}}{2}x^2-\frac{1}{3}x^3 {\Large ]}_{0}^{\sqrt[\large 3]{2}}=\frac{1}{3}$$
また、放物線と \(x\) 軸で囲まれた面積は、$$~~~~~~-\int_{0}^{1}x(x-1)dx$$$$~=-{\Large [} \frac{1}{3}x^3-\frac{1}{2}x^2 {\Large ]}_{0}^{1}=\frac{1}{6}$$したがって、放物線と直線で囲まれた図形の面積は \(x\) 軸で2等分される [終]
20
\({\small (1)}~y=-2x-1\)
\({\small (2)}~y=4x-4\)
\({\small (3)}~{\large \frac{9}{4}}\)
演習問題 微分法と積分法
演習問題A
1
\({\small (1)}~\)
\(x=0\) で極大値 \(0\)
\(x={\large \frac{2}{3}}a\) で極小値 \({\large \frac{4}{27}}a^3\)
\({\small (2)}~\)
極値なし
\({\small (3)}~\)
\(x={\large \frac{2}{3}}a\) で極大値 \({\large \frac{4}{27}}a^3\)
\(x=0\) で極小値 \(0\)
2
半径 \(2\sqrt{2}\)、高さ \(4\)、体積 \({\large \frac{32}{3}}\pi\)
3
[証明]
(左辺)
\(=\int_{0}^{1}(p^2x^2+2pqx+q^2)dx\)
\(={\Large [} {\large \frac{p^2}{3}}x^3+pqx^+q^2x {\Large ]}_{0}^{1}\)
\(={\large \frac{p^2}{3}}+pq+q^2\)
(右辺)
\(=\left\{{\Large [} {\large \frac{p}{2}}x^2+qx {\Large ]}_{0}^{1}\right\}^2\)
\(=\left({\large \frac{p}{2}}+q\right)^2\)
\(={\large \frac{p^2}{4}}+pq+q^2\)
よって、
(左辺)\(-\)(右辺)
\(=\left({\large \frac{p^2}{3}}+pq+q^2\right)\)
\(-\left({\large \frac{p^2}{4}}+pq+q^2\right)\)
\(={\large \frac{p^2}{12}}≧0\)
したがって、
\(\int_{0}^{1}(px+q)^2dx\)
\(≧\left\{\int_{0}^{1}(px+q)dx\right\}^2\)
また、等号が成立するのは \(p=0\) のとき [終]
4
[証明]
\(f(x)=x^2+1\) とすると、点 \((a,b)\) を通るので、\(b=a^2+1\)
また、微分すると \(f'(x)=2x\) より、接線の傾きが \(2a\)
よって、接戦の方程式は
\(y-(a^2+1)=2a(x-a)\)
\(~\Leftrightarrow~y=2ax-a^2+1\)
この接線と放物線 \(y=x^2\) の交点は
\(2ax-a^2+1=x^2\)
\(~\Leftrightarrow~\{x-(a-1)\}\{x-(a+1)\}=0\)
これより、\(x\) 座標は \(x=a-1~,~a+1\)
直線と放物線との面積 \(S\) は、
\(\int_{a-1}^{a+1}\{2ax-a^2+1-x^2\}dx\)
\(={\Large [} {\large \frac{1}{3}}x^3+ax^2-(a^2-1)x {\Large ]}_{a-1}^{a+1}\)
\(={\large \frac{4}{3}}\)
したがって、\(a\) の値に関係なく面積は一定となる [終]
演習問題B
5
\(0<a<1~,~4<a\) のとき、
\(x=a\) で最大値 \(a(a-3)^2\)
\(1≦a<4\) のとき、
\(x=1\) で最大値 \(4\)
\(a=4\) のとき、
\(x=1~,~4\) で最大値 \(4\)
6
\(a=2\) のとき最大値 \(6\)
\(a=1\) のとき最小値 \(1\)
7
\(f(x)=x^2-{\large \frac{2}{3}}x-{\large \frac{4}{3}}\)
8
\(m=1\)


