文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第2章 図形の性質
第1節 平面図形
問1
[証明]
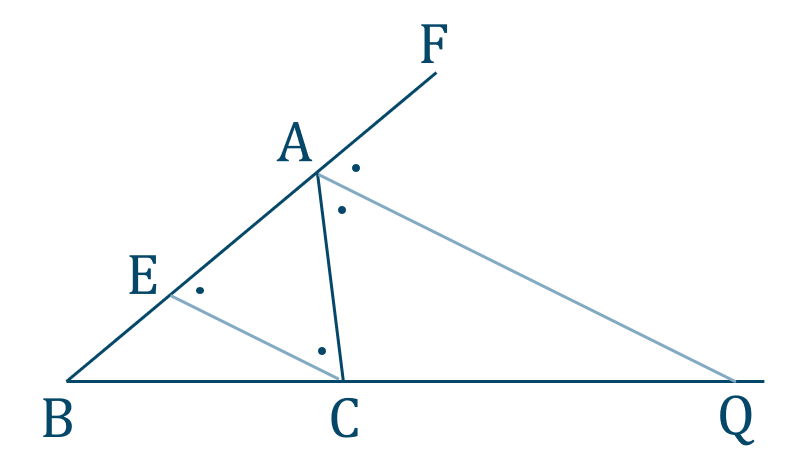
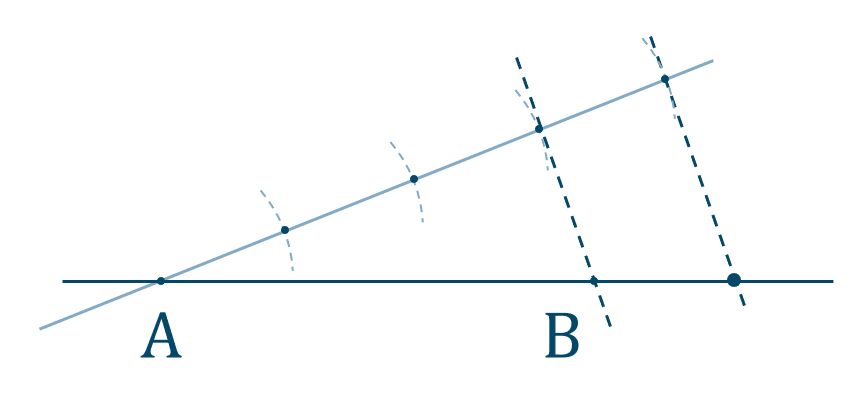
図のように、\({\rm AB}\) の延長線上に点 \({\rm F}\)
\({\rm AQ\parallel EC}\) となるように、\({\rm AB}\) 上に点 \({\rm E}\) をとる
角の二等分線より、
\(\angle{\rm FAQ}=\angle{\rm CAQ}\) …①
の同位角より、
\(\angle{\rm FAQ}=\angle{\rm AEC}\) …②
の錯角より、
\(\angle{\rm CAQ}=\angle{\rm ACE}\) …③
①、②、③より
\(\angle{\rm AEC}=\angle{\rm ACE}\)
よって、\(\triangle{\rm AEC}\) は \({\rm AE=AC}\) の二等辺三角形となる
また、\({\rm AQ\parallel EC}\) の平行線と線分の比より
\({\rm BD}:{\rm CQ}={\rm BA}:{\rm EA}\)
\({\rm AE=AC}\) とすると、
\({\rm BQ}:{\rm QC}={\rm AB}:{\rm AC}\) [終]
練習4
[証明]
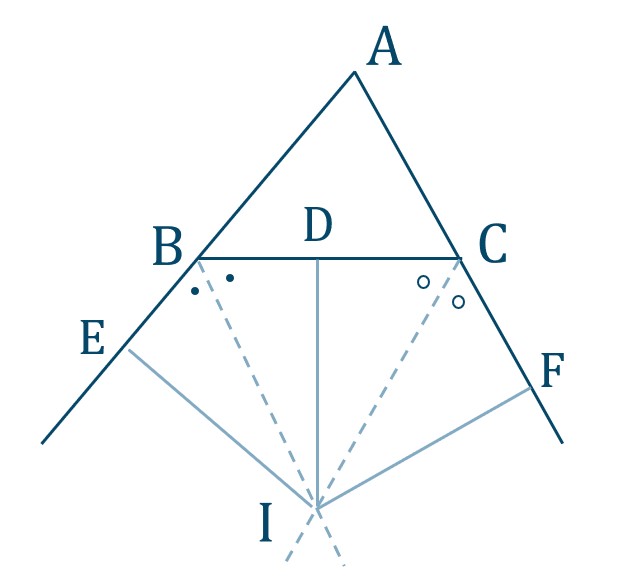
図より、点 \({\rm I}\) から
線分 \({\rm BC}\) に下ろした垂線を \({\rm ID}\)
直線 \({\rm AB}\) に下ろした垂線を \({\rm IE}\)
直線 \({\rm AC}\) に下ろした垂線を \({\rm IF}\)
とすると、
\(\triangle {\rm IBE}\equiv\triangle {\rm IBD}\) より、
\({\rm IE=ID}\)
\(\triangle {\rm ICF}\equiv\triangle {\rm ICD}\) より、
\({\rm IF=ID}\)
よって、
\({\rm IE=IF}\)
また、共通の辺より、
\({\rm AI=AI}\)
これより、斜辺と他の1辺が等しいので、
\(\triangle {\rm AIE}\equiv\triangle {\rm AIF}\)
よって、
\(\angle{\rm EAI}=\angle{\rm FAI}\)
したがって、点 \({\rm I}\) は \({\rm \angle A}\) の二等分線上にある [終]
練習6
\(11:3\)
練習9
[証明]
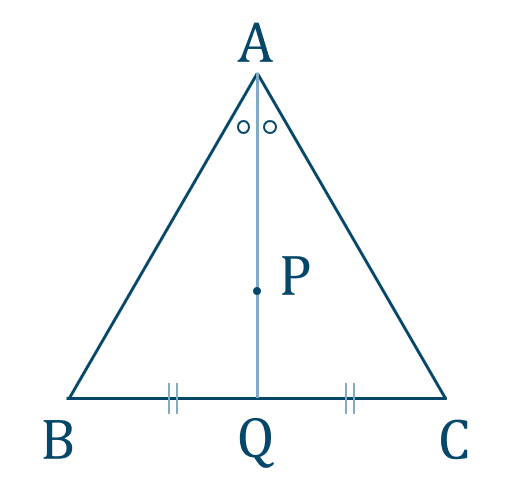
重心と内心が一致する点を \({\rm P}\) とすると、直線 \({\rm AP}\) と線分 \({\rm BC}\) との交点を \({\rm Q}\) とする
重心であることより、
\({\rm BQ:QC}=1:1\)
内心であることより、\({\rm AQ}\) は \(\angle{\rm A}\) の二等分線となり、
\(\angle{\rm BAQ}=\angle{\rm CAQ}\)
ここで、角の二等分線と比の関係より、
\({\rm AB:AC=BQ:QC}=1:1\)
よって、
\({\rm AB=AC}\)
同様に \(\angle{\rm B}\) のときも考えて、
\({\rm AB=BC}\)
したがって、\({\rm AB=BC=AC}\) となり3辺が等しいので、\(\triangle {\rm ABC}\) は正三角形である [終]
研究1
[証明]
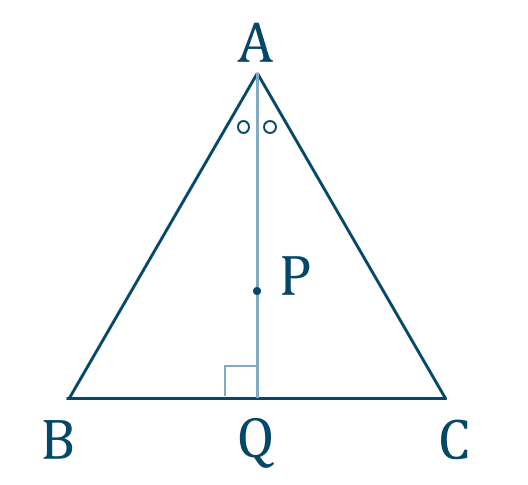
内心と垂心が一致する点を \({\rm P}\) とすると、直線 \({\rm AP}\) と線分 \({\rm BC}\) との交点を \({\rm Q}\) とする
内心であることより、\({\rm AQ}\) は \(\angle{\rm A}\) の二等分線となり、
\(\angle{\rm BAQ}=\angle{\rm CAQ}\)
垂心であることより、
\(\angle{\rm AQB}=\angle{\rm AQC}=90^\circ\)
また、共通の辺より、
\({\rm AQ=AQ}\)
1辺とその両端の角がそれぞれ等しいので、
\(\triangle {\rm ABQ}\equiv\triangle {\rm ACQ}\)
よって、
\({\rm AB=AC}\)
同様に \(\angle{\rm B}\) のときも考えて、
\({\rm AB=BC}\)
したがって、\({\rm AB=BC=AC}\) となり3辺が等しいので、\(\triangle {\rm ABC}\) は正三角形である [終]
→ 三角形の垂心
練習12
\({\small (1)}~2:1\)
\({\small (2)}~1:2\)
研究2
[証明]
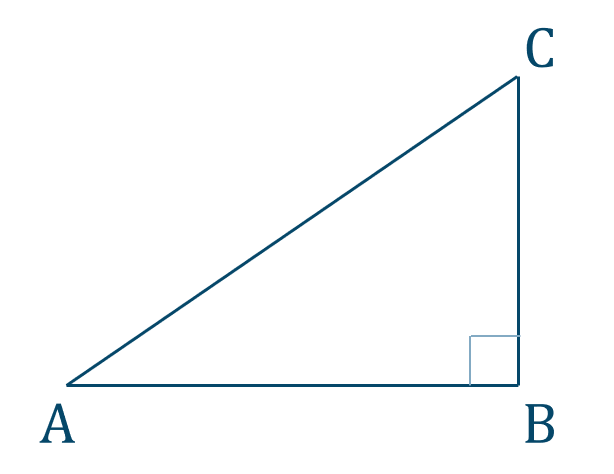
図において、\(\angle{\rm B}=90^\circ\) より、
\(\angle{\rm A}+\angle{\rm C}=90^\circ\)
よって、\(\angle{\rm A}<90^\circ~,~\angle{\rm C}<90^\circ\) となり、
\(\angle{\rm A}<\angle{\rm B}~,~\angle{\rm C}<\angle{\rm B}\)
これより、\(\angle{\rm B}\) が最大の角となり、向かい合う斜辺 \({\rm AC}\) が最も大きい辺となる [終]
→ 三角形の辺と角の大小比較
練習13
\({\small (1)}~24^\circ\) \({\small (2)}~28^\circ\)
練習15
\({\small (1)}~88^\circ\) \({\small (2)}~52^\circ\)
\({\small (3)}~124^\circ\)
→ 円に内接する四角形と角
練習16
[証明]
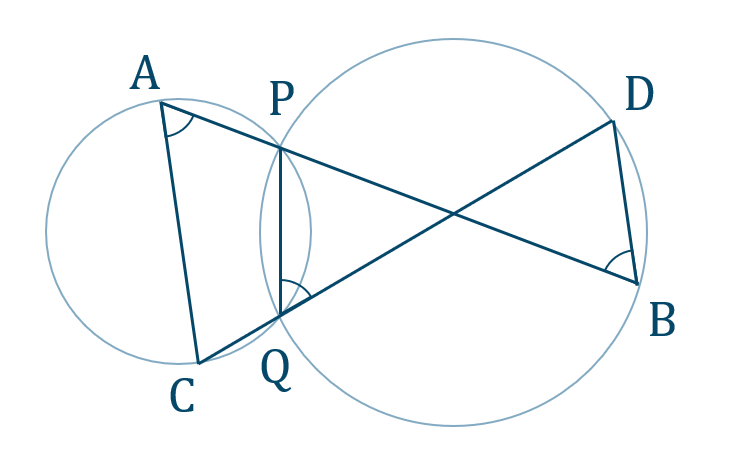
四角形 \({\rm ACQP}\) は円に内接するので、対角の外角の条件より、
\(\angle{\rm PAC}=\angle{\rm PQD}\)
次に、弧 \({\rm PD}\) に対する円周角の定理より、
\(\angle{\rm PQD}=\angle{\rm PBD}\)
よって、
\(\angle{\rm PAC}=\angle{\rm PBD}\)
したがって、錯覚が等しいので、
\({\rm AC\parallel DB}\) [終]
練習17
[証明]
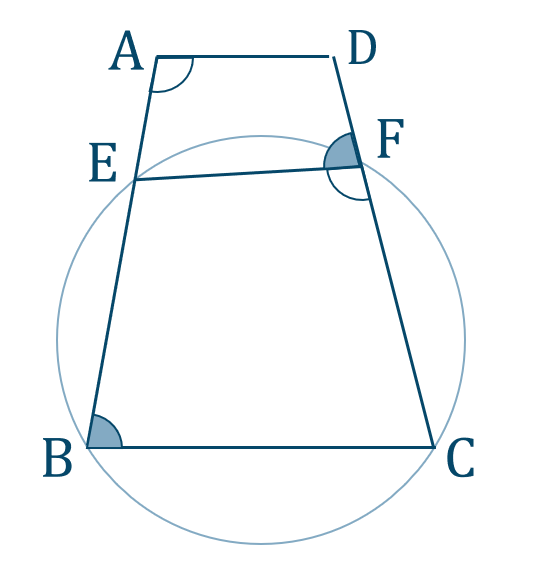
四角形 \({\rm BCFE}\) は円に内接するので、対角の外角の条件より、
\(\angle{\rm EBC}=\angle{\rm DFE}\)
また、\({\rm AD\parallel BC}\) より、
\(\angle{\rm EBC}+\angle{\rm EAD}=180^\circ\)
よって、
\(\angle{\rm DFE}+\angle{\rm EAD}=180^\circ\)
したがって、内角の和が \(180^\circ\) となるので、四角形 \({\rm AEFD}\) は円に内接する [終]
問2
[証明]
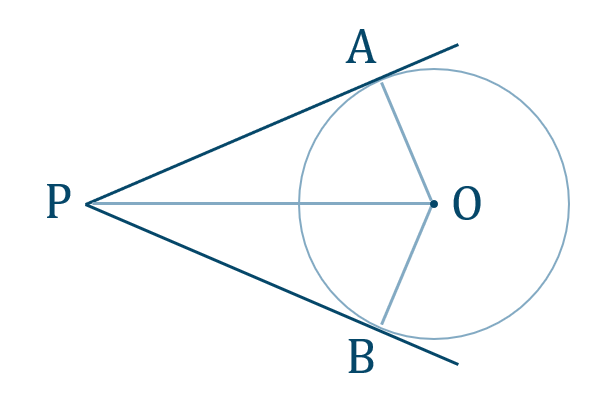
円の中心を \({\rm O}\) 、接点を \({\rm A~,~B}\) 、接点の交点を \({\rm P}\) とすると、
\(\triangle {\rm OPA}\) と \(\triangle {\rm OPB}\) において、接線の条件より、
\(\angle{\rm OAP}=\angle{\rm OBP}=90^\circ\)
円の半径より、
\({\rm OA=OB}\)
共通な辺より、
\({\rm OP=OP}\)
直角三角形の斜辺と他の1辺がそれぞれ等しいので、
\(\triangle {\rm OPA}\equiv\triangle {\rm OPB}\)
したがって、
\({\rm PA=PB}\) [終]
練習19
[証明]
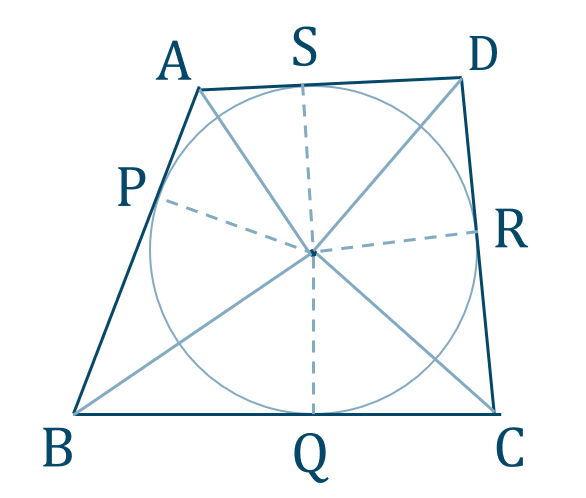
この円の半径を \(r\) とすると、
\({\rm OP=OQ=OR=OS}=r\)
また、\({\rm AB~,~BC~,~CD~,~DA}\) は円の接線であることより、
\({\rm OP\perp AB~,~OQ\perp BC}\)
\({\rm OR\perp CD~,~OS\perp DA}\)
よって、
\(\triangle {\rm OAB}+\triangle {\rm OCD}\)
\(={\large \frac{1}{2}}\cdot r \cdot {\rm AB}+{\large \frac{1}{2}}\cdot r \cdot {\rm CD}\)
\(={\large \frac{1}{2}}r({\rm AB+CD})\)
また、
\(\triangle {\rm OBC}+\triangle {\rm ODA}\)
\(={\large \frac{1}{2}}\cdot r \cdot {\rm BC}+{\large \frac{1}{2}}\cdot r \cdot {\rm DA}\)
\(={\large \frac{1}{2}}r({\rm BC+DA})\)
ここで、円に外接する四角形の条件より、
\({\rm AB+CD=BC+DA}\)
したがって、
\(\triangle {\rm OAB}+\triangle {\rm OCD}=\triangle {\rm OBC}+\triangle {\rm ODA}\)
[終]
問3
[証明]
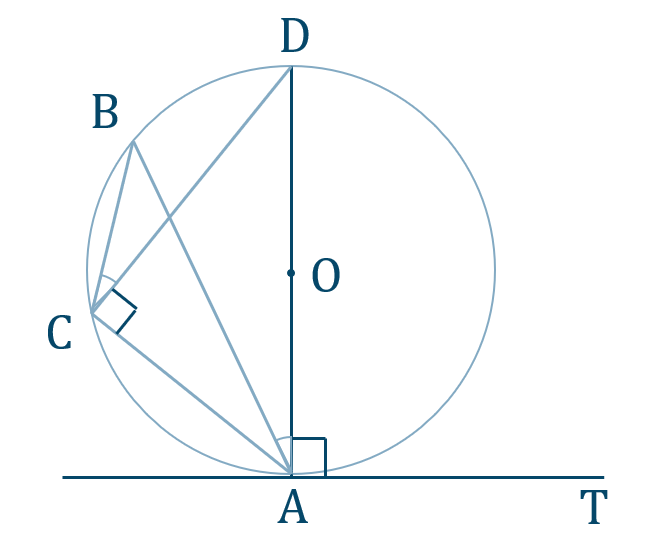
円の直径を \({\rm AD}\) とするの、直径の円周角の定理より、
\(\angle{\rm DCA}=90^\circ\)
円の接線より、
\(\angle{\rm DAT}=90^\circ\)
ここで、弧 \({\rm BD}\) の円周角の定理より、
\(\angle{\rm BCD}=\angle{\rm BAD}\)
よって、
\(\angle{\rm BCA}=\angle{\rm BCD}+90^\circ\)
\(\angle{\rm BAT}=\angle{\rm BAD}+90^\circ\)
したがって、
\(\angle{\rm BAT}=\angle{\rm BCA}\) [終]
練習22
\(\sqrt{2}\)
練習23
[証明]
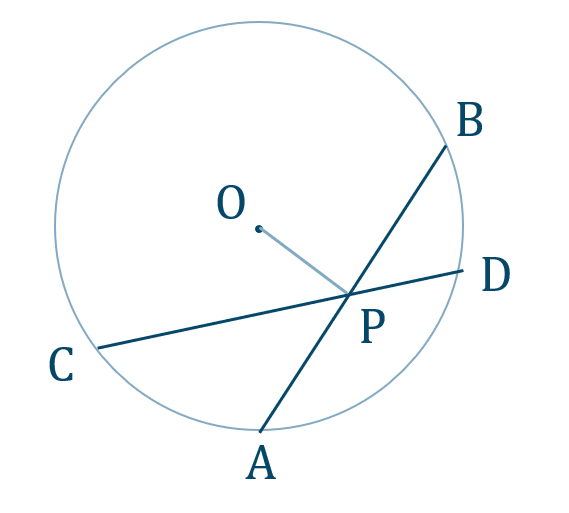
弦の性質より、
\({\rm PA=PB}\)
また、方べきの定理より、
\({\rm PC\cdot PD=PA\cdot PB}\)
したがって、
\({\rm PC\cdot PD=PA^2}\) [終]
問4
[証明]
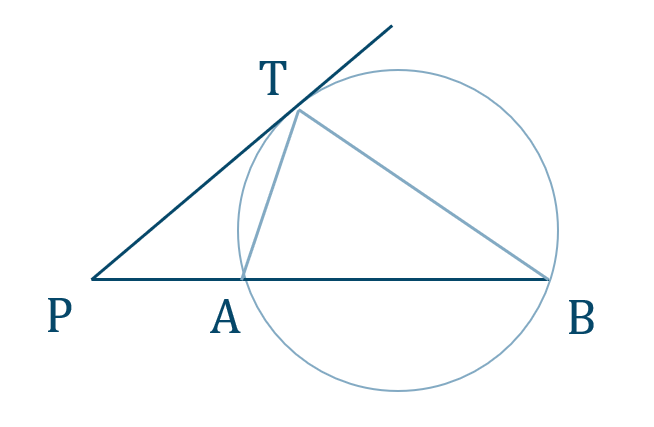
\(\triangle {\rm PTA}\) と \(\triangle {\rm PBT}\) において、
共通の角より、
\(\angle{\rm TPA}=\angle{\rm BPT}\)
\({\rm PT}\) が接線であり、接弦定理より、
\(\angle{\rm PTA}=\angle{\rm PBT}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm PTA}\sim\triangle {\rm PBT}\)
よって、
\({\rm PT:PA=PB:PT}\)
したがって、
\({\rm PA\cdot PB=PT^2}\) [終]
練習24
[証明]
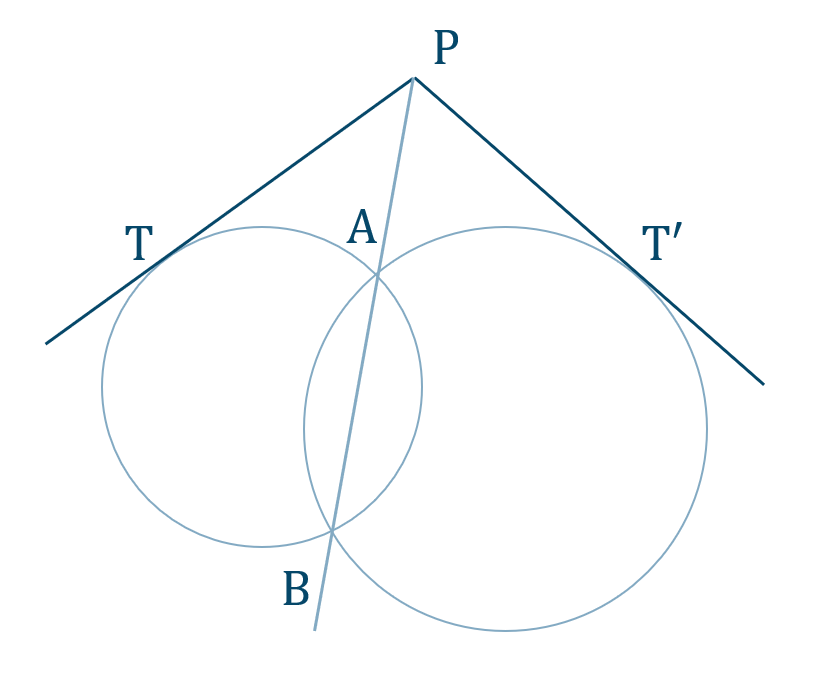
左側の円について、方べきの定理より、
\({\rm PT^2=PA\cdot PB}\)
右側の円について、方べきの定理より、
\({\rm PT’^2=PA\cdot PB}\)
よって、
\({\rm PT^2=PT’^2}\)
したがって、
\({\rm PT=PT’}\) [終]
練習25
[証明]
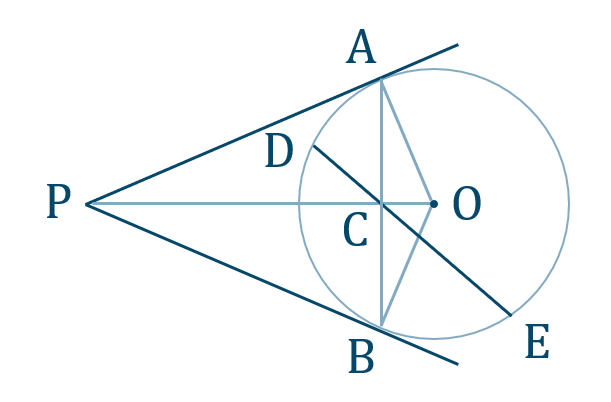
円 \({\rm O}\) について、方べきの定理より、
\({\rm CD\cdot CE=CA\cdot CB}\) …①
次に、\(\angle{\rm OAP}=90^\circ\) かつ \(\angle{\rm OBP}=90^\circ\) であり、向かい合う角の和が \(180^\circ\) となるので、四角形 \({\rm APBO}\) は同一円周上にある
よって、方べきの定理より、
\({\rm CP\cdot CO=CA\cdot CB}\) …②
①と②より、
\({\rm CD\cdot CE=CP\cdot CO}\)
したがって、方べきの定理の逆より、4点 \({\rm P~,~O~,~D~,~E}\) は同一円周上にある [終]
練習26
\({\small (1)}~>\) \({\small (2)}~=\) \({\small (3)}~<~,~<\)
\({\small (4)}~=\) \({\small (5)}~<\)
→ 2つの円の位置関係と共通接線
練習28
\(60^\circ\)
問5
練習33

研究1
\({\small (1)}~\)[証明] 正五角形 \({\rm ABCDE}\) は円に内接しており、\({\rm CD=BC}\) の同じ弦に対する円周角の定理より、
\(\angle{\rm CAD}=\angle{\rm FDC}=a\) …①
同様に、
\(\angle{\rm BAC}=\angle{\rm CBD}=\angle{\rm ACE}=\angle{\rm ECD}=a\)
\(\triangle {\rm BFC}\) の \(\angle{\rm BFC}\) の外角の条件より、
\(\angle{\rm DFC}=\angle{\rm CBF}+\angle{\rm BCA}=2a\)
次に、弧 \({\rm AD}\) における円周角より、
\(\angle{\rm ACD}=\angle{\rm ACE}+\angle{\rm ECD}=2a\)
よって、
\(\angle{\rm ACD}=\angle{\rm DFC}\) …②
①と②より、2組の角がそれぞれ等しいので、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm DFC}\) は二等辺三角形より、
\({\rm CD=DF}=1\)
\(\triangle {\rm AFD}\) は二等辺三角形より、
\({\rm FD=FA}=1\)
よって、
\({\rm FC=AC-FA}=x-1\)
(1) より、
\(\triangle {\rm ACD}\sim\triangle {\rm DFC}\)
よって、
\({\rm AC:DF=CD:FC}\)
したがって、
\(x:1=1:x-1\) [終]
\({\small (3)}~\)[証明] (2) より、
\(x:1=1:x-1\)
これより、
\(x(x-1)=1\)
\(x^2-x-1=0\)
解の公式より、
\(x={\large \frac{1\pm \sqrt{5}}{2}}\)
ここで、\(x>0\) より、
\(x={\large \frac{1+\sqrt{5}}{2}}\)
また、\({\rm CD:AC}=1:x\) より、
\({\rm CD:AC}=1:{\large \frac{1+\sqrt{5}}{2}}\) [終]
研究2

問題
1
\({\small (1)}~3:2\)
\({\small (2)}~30:7\)
2
\({\small (1)}~3\) \({\small (2)}~2\)
3
\({\small (1)}~\alpha=20^\circ~,~\beta=60^\circ\)
\({\small (2)}~56^\circ\)
4
\({\small (1)}~5\) \({\small (2)}~{\large \frac{12}{5}}\)
5
[証明] 四角形 \({\rm ADCB}\) は円に内接するので、外角の条件より、
\(\angle{\rm ABC}=\angle{\rm APE}\)
四角形 \({\rm ABDQ}\) は円に内接するので、外角の条件より、
\(\angle{\rm ABD}=\angle{\rm AQE}\)
ここで、
\(\angle{\rm ABC}+\angle{\rm ABD}=180^\circ\)
これより、
\(\angle{\rm APE}+\angle{\rm AQE}=180^\circ\)
対角の和が \(180^\circ\) となるので、四角形 \({\rm EPAQ}\) は円に内接する [終]
6
[証明]
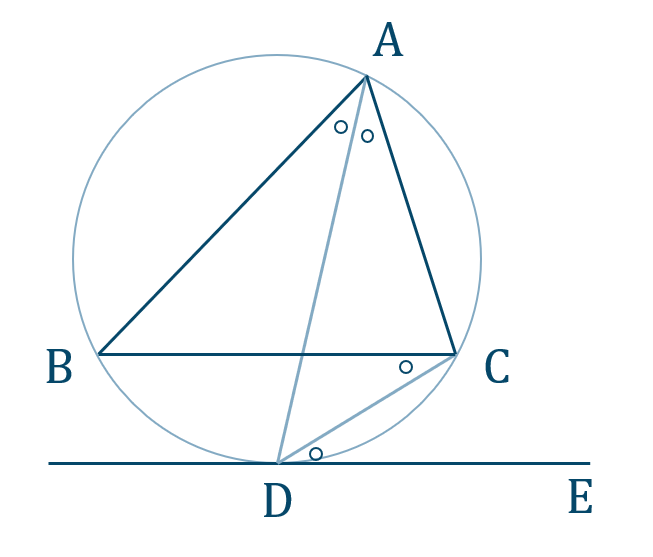
図のように、\(l\) 上の点 \({\rm E}\) をとると、接線と円の条件より、
\(\angle{\rm CDE}=\angle{\rm CAD}\)
弧 \({\rm BD}\) に対する円周角より、
\(\angle{\rm BAD}=\angle{\rm BCD}\)
仮定より、\(\angle{\rm A}\) の二等分線となるので、
\(\angle{\rm BAD}=\angle{\rm DAC}\)
よって、
\(\angle{\rm CDE}=\angle{\rm BCD}\)
したがって、錯角が等しいので、
\(l\parallel{\rm BC}\) [終]
7
[証明] 図のように、点 \({\rm P}\) における共通接線を引き、この線上の点を \({\rm E~,~F}\) とする
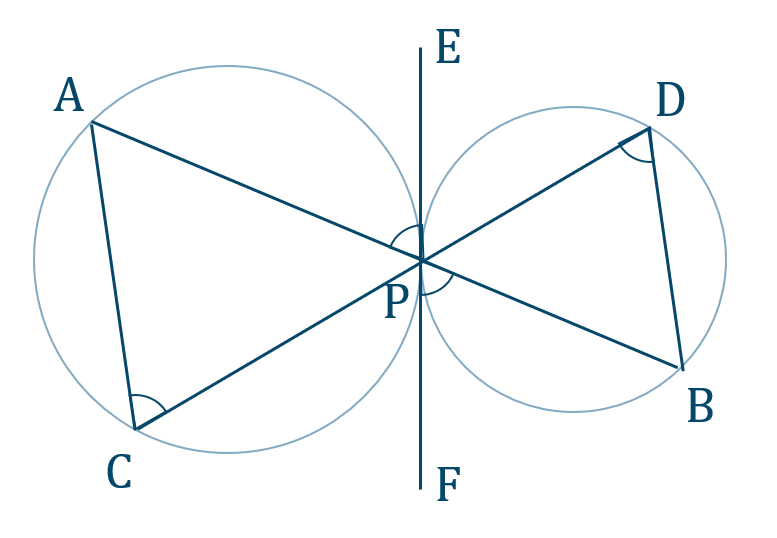
\(\triangle {\rm ACP}\) の接弦定理より、
\(\angle{\rm ACP}=\angle{\rm APE}\)
\(\triangle {\rm BDP}\) の接弦定理より、
\(\angle{\rm BDP}=\angle{\rm BPF}\)
ここで、対頂角が等しいので、
\(\angle{\rm APE}=\angle{\rm BPF}\)
よって、
\(\angle{\rm ACP}=\angle{\rm BDP}\)
したがって、錯角が等しいので、
\({\rm AC\parallel DB}\) [終]
8
第2節 空間図形
練習35
\({\small (1)}~90^\circ\) \({\small (2)}~45^\circ\)
\({\small (3)}~90^\circ\)
練習36
\({\small (1)}~\)[証明] \(\triangle {\rm ACD}\) は正三角形で、点 \({\rm M}\) は \({\rm CD}\) の中点となるので、
\({\rm CD\perp AM}\)
同様に、\(\triangle {\rm BCD}\) において、
\({\rm CD\perp BM}\)
したがって、辺 \({\rm CD}\) は平面 \({\rm ABM}\) に垂直である [終]
\({\small (2)}~\)[証明] (1) より、辺 \({\rm CD}\) は平面 \({\rm ABM}\) に垂直であり、辺 \({\rm AB}\) は平面 \({\rm ABM}\) 上にある
したがって、
\({\rm AB\perp CD}\) [終]
練習37
\({\small (1)}~\)正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しくない
\({\small (4)}~\)正しくない
\({\small (5)}~\)正しい
研究1
\({\small (1)}~\)[証明] \(\triangle {\rm ACD}\) と \(\triangle {\rm BCD}\) において、
仮定より、
\({\rm AC=BC}\) …①
\({\rm AD=BD}\) …②
共通な辺より、
\({\rm CD=CD}\) …③
①?③より、3辺がそれぞれ等しいので、
\(\triangle {\rm ACD}\equiv\triangle {\rm BCD}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm ACE}\) と \(\triangle {\rm BCE}\) において、
\(\triangle {\rm ACD}\equiv\triangle {\rm BCD}\) より、
\(\angle{\rm ACE}=\angle{\rm BCE}\) …①
仮定より、
\({\rm AC=BC}\) …②
共通な辺より、
\({\rm CE=CE}\) …③
①?③より、2辺とその間の角がそれぞれ等しいので、
\(\triangle {\rm ACE}\equiv\triangle {\rm BCE}\) [終]
\({\small (3)}~\)[証明] \(\triangle {\rm ACE}\equiv\triangle {\rm BEC}\) より、
\(\angle{\rm AEC}=\angle{\rm BEC}=90^\circ\)
よって、
\({\rm AE\perp CD}\)
また、仮定より、
\({\rm HE\perp CD~,~AH\perp HE}\)
したがって、三垂線の定理より \({\rm AH}\) は平面 \({\rm BCD}\) に垂直である [終]
練習38
正四面体 \(4\) 正三角形 \(4\) \(6\)
正六面体 \(6\) 正方形 \(8\) \(12\)
正十二面体 \(12\) 正五角形 \(20\) \(30\)
正二十面体 \(20\) 正三角形 \(12\) \(30\)
練習39
それぞれ表より、\(v-e+f\) を求めると
正四面体 \(4-6+4=2\)
正六面体 \(8-12+6=2\)
正八面体 \(6-12+8=2\)
正十二面体 \(20-30+12=2\)
正二十面体 \(12-30+20=2\)
よって、これらの正多面体のおいて、
\(v-e+f=2\) が成り立つ
練習40
\({\small (1)}~\)
面 \(14\) 、頂点 \(12\) 、辺 \(24\)
\({\small (2)}~\)
\(v=12~,~e=24~,~f=14\) より、①に代入すると、
\(12-24+14=2\)
したがって、①が成り立つ
練習41
\({\small (1)}~\)
1つの頂点に集まる角の和が \(360^\circ\) より小さく、正方形の1つの内角が \(90^\circ\) より、
\(360^\circ \div 90^\circ =4\)
よって、1つの頂点に集まる正方形の数は4より小さい
また、1つの頂点に集まる面の数は3以上なので、1つの頂点に集まる正方形は3つとなる
よって、
\(v={\large \frac{4f}{3}}\)
また、1つの辺に集まる面の数は2つであるので、
\(e={\large \frac{4f}{2}}\)
\(v-e+f=2\) より、
\({\large \frac{4f}{3}}-{\large \frac{4f}{2}}+f=2\)
これより、\(f=6\) となり、
各面が正方形である正多面体が存在するならば、その面の数は6である
\({\small (2)}~\)1つの頂点に集まる角の和が \(360^\circ\) より小さく、正三角形の1つの内角が \(60^\circ\) より、
\(360^\circ \div 60^\circ =6\)
よって、1つの頂点に集まる正方形の数は6より小さい
また、1つの頂点に集まる面の数は3以上なので、1つの頂点に集まる正三角形は3か4か5となる
( ⅰ ) 3のとき、\(v={\large \frac{3f}{3}}~,~e={\large \frac{3f}{2}}\)
\(v-e+f=2\) より、
\({\large \frac{3f}{3}}-{\large \frac{3f}{2}}+f=2\)
これより、\(f=4\)
( ⅱ ) 4のとき、\(v={\large \frac{3f}{4}}~,~e={\large \frac{3f}{2}}\)
\(v-e+f=2\) より、
\({\large \frac{3f}{4}}-{\large \frac{3f}{2}}+f=2\)
これより、\(f=8\)
( ⅲ ) 5のとき、\(v={\large \frac{3f}{5}}~,~e={\large \frac{3f}{2}}\)
\(v-e+f=2\) より、
\({\large \frac{3f}{5}}-{\large \frac{3f}{2}}+f=2\)
これより、\(f=20\)
したがって、各面が正三角形である正多面体が存在するならば、その面の数は \(4\) か \(8\) か \(20\) である
練習42
\({\large \frac{\sqrt{2}}{12}}a^3\)
問題
9
\({\small (1)}~\)正しくない
\({\small (2)}~\)正しい
\({\small (3)}~\)正しくない
10
\({\small (1)}~\)
[証明] \({\rm OA\perp OB~,~OA\perp OC}\) より、
\({\rm OA}\perp\triangle {\rm OBC}\)
よって、\({\rm BC}\) は \(\triangle {\rm OBC}\) 上の辺であるので、
\({\rm OA\perp BC}\) [終]
[証明] \({\rm OH}\perp\triangle {\rm ABC}\) より、辺 \({\rm BC}\) は \(\triangle {\rm ABC}\) の辺より、
\({\rm OH\perp BC}\) [終]
\({\small (2)}~\)
[証明] (1) より、
\({\rm OA\perp BC~,~OH\perp BC}\)
これより、
\({\rm BC}\perp\triangle {\rm OAH}\)
ここで、辺 \({\rm AH}\) は \(\triangle {\rm OAH}\) 上の辺であるので、
\({\rm AH\perp BC}\) [終]
11
頂点 \(60\)、辺 \(90\)
12
\({\small (1)}~\)正八面体
\({\small (2)}~{\large \frac{{\rm V}}{2}}\)
演習問題 図形の性質
演習問題A
1
[証明] \(\triangle {\rm AMB}\) において、角の二等分線と比の関係より、
\({\rm MA:MB=AD:DB}\)
\(\triangle {\rm AMC}\) において、角の二等分線と比の関係より、
\({\rm MA:MC=AE:EC}\)
仮定より、\({\rm MB=MC}\) であるので、
\({\rm AD:DB=AE:EC}\)
平行線と比の関係より、
\({\rm DE\parallel BC}\) [終]
2
\({\small (1)}~\)[証明]
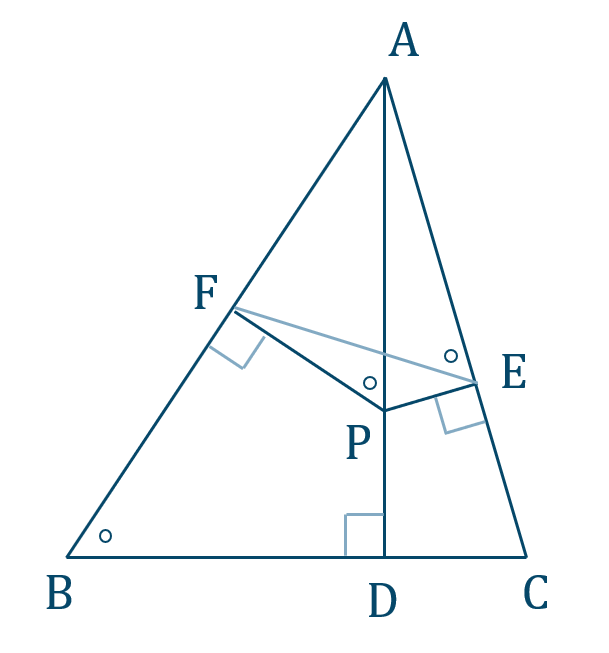
対角の和が \(180^\circ\) より、四角形 \({\rm AFDE}\) は円に内接する
よって、円周角の定理より、
\(\angle{\rm APF}=\angle{\rm AEF}\) [終]
\({\small (2)}~\)[証明] 対角の和が \(180^\circ\) より、四角形 \({\rm FBDP}\) は円に内接する
よって、内角と対角の外角は等しいので、
\(\angle{\rm APF}=\angle{\rm FBD}\) [終]
\({\small (3)}~\)[証明] (1)、(2)より、
\(\angle{\rm AEF}=\angle{\rm FBD}\)
したがって、四角形 \({\rm BCEF}\) は内角と対角の外角が等しいくなるので円に内接する [終]
3
\({\small (1)}~\)[証明]
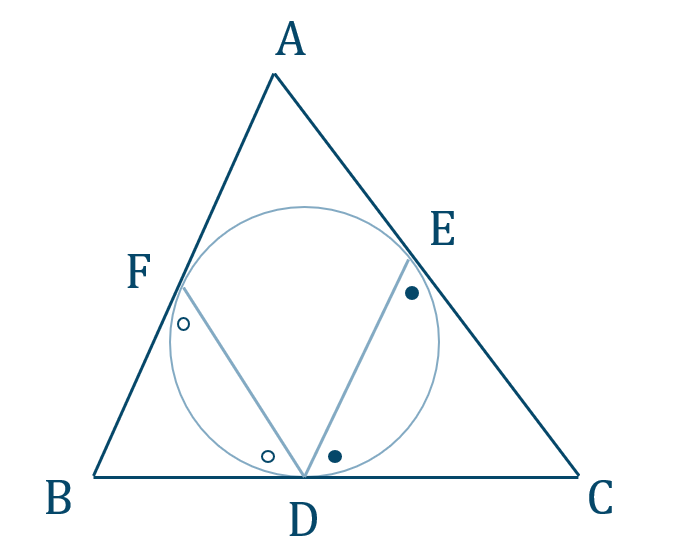
三角形の内接円の条件より、
\({\rm BF=BD}\)
\(\triangle {\rm BDF}\) は二等辺三角形で、
\(\angle{\rm BDF}=\angle{\rm BFD}=x\)
これより、
\(\angle{\rm ABC}=180^\circ-2x\) …①
同様に、\({\rm CE=CD}\) となり、\(\triangle {\rm CDE}\) は二等辺三角形で、
\(\angle{\rm CDE}=\angle{\rm CED}=y\)
これより、
\(\angle{\rm ACB}=180^\circ-2y\) …②
また、点 \({\rm D}\) について、
\(\angle{\rm FDE}=180^\circ-(x+y)\)
両辺を2倍すると、
\(2\angle{\rm FDE}=360^\circ-2x-2y)\)
①+②より、
\(2\angle{\rm FDE}=\angle{\rm ABC}+\angle{\rm ACB}\) [終]
\({\small (2)}~\)[証明] 三角形の内接円の条件より、
\({\rm AF=AE~,~BF=BD~,~CE=CD}\)
次に、
\({\rm AB=AF+BF}\) …①
\({\rm AC=AE+CE}\) …②
\({\rm BC=BD+CD}\) …③
①+②?③より、
\({\rm AB+AC-BC}\)
\(={\rm AF+BF+AE+CE-BD-CD}\)
\(={\rm AF+AE}\)
\(=2{\rm AF}\)
したがって、
\(2{\rm AF=AB+AC-BC}\) [終]
4
\({\small (1)}~9:2\)
\({\small (2)}~3:2\)
\({\small (3)}~1:2\)
演習問題B
5
\({\small (1)}~\)[証明] \(\triangle {\rm ABE}\) と \(\triangle {\rm ACD}\) において、
仮定より、
\(\angle{\rm BAE}=\angle{\rm CAD}\)
弧 \({\rm AD}\) に対する円周角より、
\(\angle{\rm ABE}=\angle{\rm ACD}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm ABE}\sim\triangle {\rm ACD}\) [終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm AED}\) において、
\(\angle{\rm BAC}=\angle{\rm BAE}+\angle{\rm EAC}\)
\(\angle{\rm EAD}=\angle{\rm CAD}+\angle{\rm EAC}\)
仮定より \(\angle{\rm BAE}=\angle{\rm CAD}\) であるので、
\(\angle{\rm BAC}=\angle{\rm EAD}\)
次に、弧 \({\rm AB}\) に対する円周角より、
\(\angle{\rm ACB}=\angle{\rm ADE}\)
2組の角がそれぞれ等しいので、
\(\triangle {\rm ABC}\sim\triangle {\rm AED}\) [終]
\({\small (3)}~\)[証明] (1) の \(\triangle {\rm ABE}\sim\triangle {\rm ACD}\) より、
\({\rm AB:AC=BE:CD}\)
よって、
\({\rm AB\cdot CD=AC\cdot BE}\) …①
また、(2) の \(\triangle {\rm ABC}\sim\triangle {\rm AED}\) より、
\({\rm BC:ED=AC:AD}\)
よって、
\({\rm BC\cdot AD=ED\cdot AC}\) …②
①と②の両辺を加えると、
左辺は、
\({\rm AB\cdot CD=BC\cdot DA}\)
右辺は、
\({\rm AC\cdot BE+ED\cdot AC}\)
\(={\rm AC(BE+ED)}\)
\(={\rm AC\cdot BD}\)
したがって、
\({\rm AB\cdot CD+BC\cdot DA=AC\cdot BD}\) [終]
6
[証明]
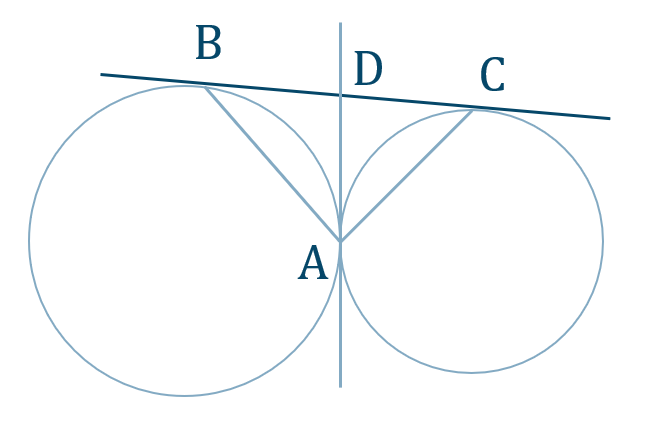
点 \({\rm A}\) における共通接線と \({\rm BC}\) との交点を \({\rm D}\) とすると、
\({\rm DA=DB=DC}\)
よって、点 \({\rm D}\) は \(\triangle {\rm ABC}\) の外接円の中心となり、線分 \({\rm BC}\) が直径となる
したがって、
\(\angle{\rm BAC}=90^\circ\) [終]
7
\({\small (1)}~\)[証明] 仮定より、
\(\angle{\rm BAE}=\angle{\rm DAC}\)
また、弧 \({\rm AD}\) における円周角の定理より、
\(\angle{\rm AEF}=\angle{\rm ACD}\)
よって、2つの角がそれぞれ等しいので、
\(\triangle {\rm ABE} \sim \triangle {\rm ADC}\)
これより、
\({\rm AB:AE=AD:AC}\)
よって、
\({\rm AB\cdot AC=AE\cdot AD}\)
ここで、\({\rm AE=AD+DE}\) より、
\({\rm AB\cdot AC=(AD+DE)\cdot AD}\)
ゆえに、
\({\rm AB\cdot AC=AD}^2+{\rm DE\cdot AD}\) …①
次に、方べきの定理より、
\({\rm AD\cdot DE=BD\cdot CD}\)
①に代入すると、
\({\rm AB\cdot AC=AD}^2+{\rm BD\cdot CD}\)
したがって、
\({\rm AD}^2={\rm AB\cdot AC-BD\cdot CD}\) [終]
\({\small (2)}~\)[証明]
\({\rm I}\) は \(\triangle {\rm ABC}\) の内心より、角の二等分線となるので、
\(\angle{\rm BAE}=\angle{\rm EAC}\)
円周角の定理の逆より、
\({\rm EB=EC}\) …①
次に、\({\rm BI}\) は角の二等分線より、
\(\angle{\rm ABI}=\angle{\rm IBD}=x\)
また、\({\rm EB=EC}\) より、
\(\angle{\rm EBD}=\angle{\rm ECB}=y\)
ここで、
\(\angle{\rm IBE}=\angle{\rm IBD}+\angle{\rm EBD}=x+y\)
\(\triangle {\rm IAB}\) の外角の条件より、
\(\angle{\rm BIE}=\angle{\rm IBA}+\angle{\rm BAI}=x+y\)
よって、\(\triangle {\rm EBI}\) は二等辺三角形となり
\({\rm EB=EI}\) …②
①、②より、
\({\rm EB=EC=EI}\) [終]
8
\({\small (1)}~{\large \frac{4\sqrt{2}}{3}}\pi\)
\({\small (2)}~{\large \frac{2\sqrt{2}}{3}}\pi\)
次のページ「第3章 整数の性質」