文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 数と式
第2章 集合と命題
第4章 図形と計量
第5章 データの分析
第3章 2次関数
第1節 2次関数とグラフ
p.69
練習1
\({\small (1)}~4\) \({\small (2)}~4\) \({\small (3)}~a^2+2a+1\) \({\small (4)}~a^2\)
練習1
\({\small (1)}~4\) \({\small (2)}~4\) \({\small (3)}~a^2+2a+1\) \({\small (4)}~a^2\)
p.69
練習2
\(y=2x~(x≧4)\)
練習2
\(y=2x~(x≧4)\)
p.70
問3
\({\small (1)}~\)第1象限 \({\small (2)}~\)第4象限
\({\small (3)}~\)第2象限 \({\small (4)}~\)第3象限
→ 関数の値と象限
問3
\({\small (1)}~\)第1象限 \({\small (2)}~\)第4象限
\({\small (3)}~\)第2象限 \({\small (4)}~\)第3象限
→ 関数の値と象限
p.71
練習4
\({\small (1)}~-2≦y≦7\)

\({\small (2)}~0≦y≦8\)

練習4
\({\small (1)}~-2≦y≦7\)
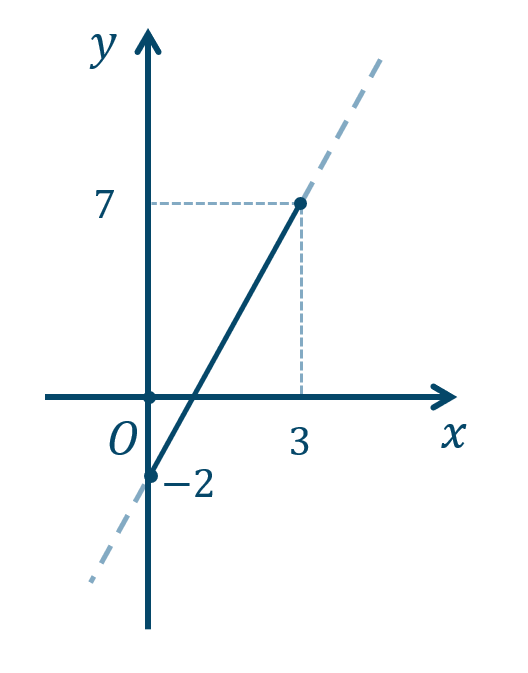
\({\small (2)}~0≦y≦8\)
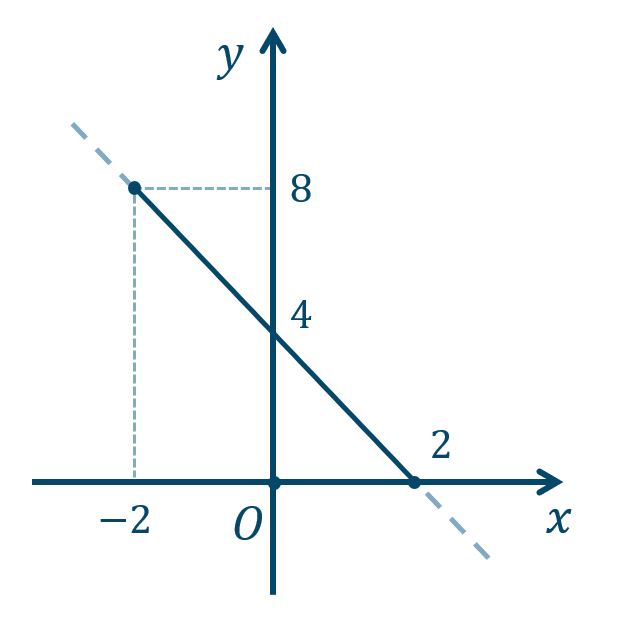
p.71
練習5
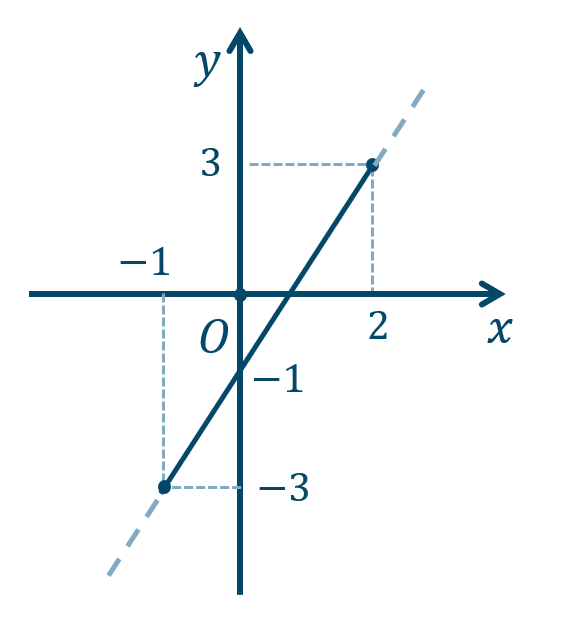
\({\small (1)}~-3≦y≦3\)
\(x=2\) で、最大値 \(3\)
\(x=-1\) で、最大値 \(-3\)

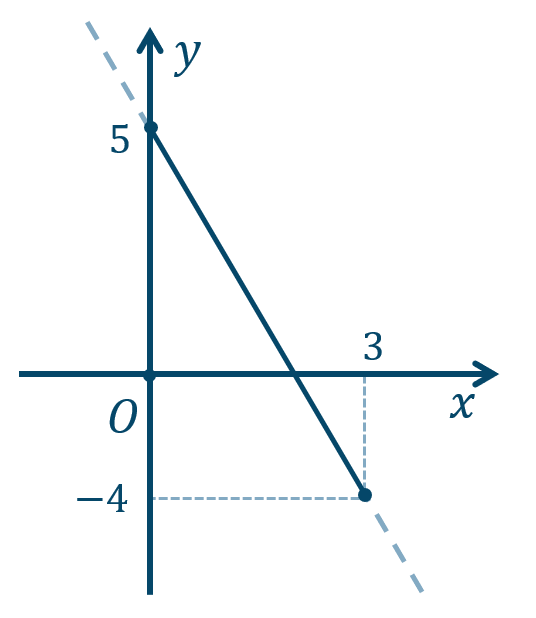
\({\small (2)}~-4≦y≦5\)
\(x=0\) で、最大値 \(5\)
\(x=3\) で、最大値 \(-4\)

→ 関数の値域と最大値・最小値
練習5
\({\small (1)}~-3≦y≦3\)
\(x=2\) で、最大値 \(3\)
\(x=-1\) で、最大値 \(-3\)
\({\small (2)}~-4≦y≦5\)
\(x=0\) で、最大値 \(5\)
\(x=3\) で、最大値 \(-4\)
→ 関数の値域と最大値・最小値
p.73
練習6
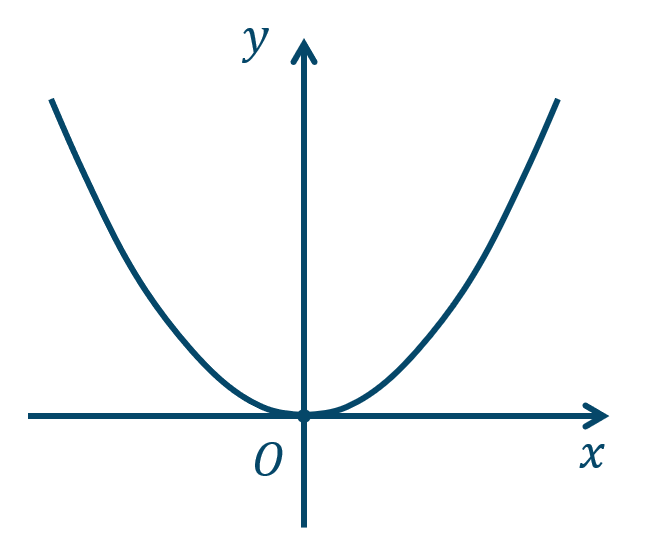
\({\small (1)}~\)下に凸

\({\small (2)}~\)上に凸

\({\small (3)}~\)下に凸

練習6
\({\small (1)}~\)下に凸

\({\small (2)}~\)上に凸
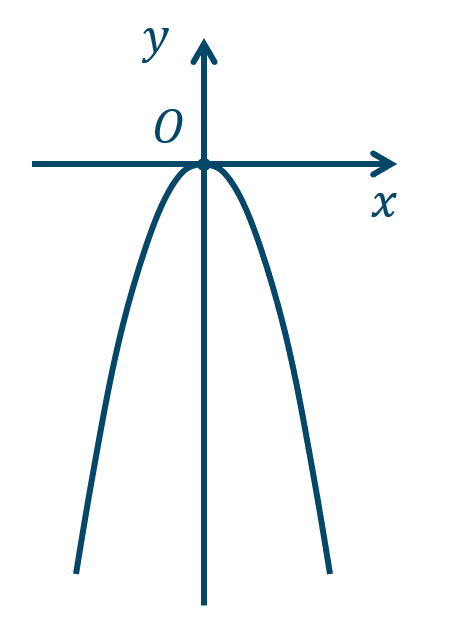
\({\small (3)}~\)下に凸
p.74
練習7
\({\small (1)}~\)軸は \(y\) 軸、頂点 \((0,3)\)

\({\small (2)}~\)軸は \(y\) 軸、頂点 \((0,-1)\)

\({\small (3)}~\)軸は \(y\) 軸、頂点 \((0,2)\)

練習7
\({\small (1)}~\)軸は \(y\) 軸、頂点 \((0,3)\)
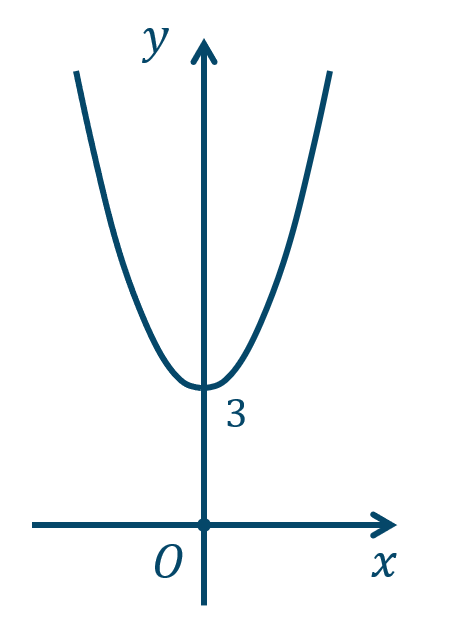
\({\small (2)}~\)軸は \(y\) 軸、頂点 \((0,-1)\)
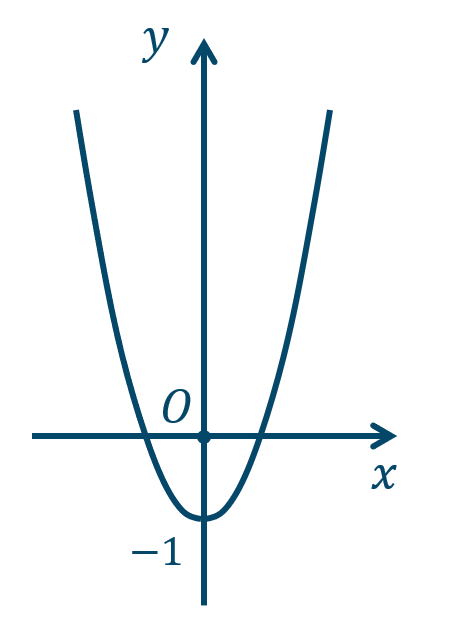
\({\small (3)}~\)軸は \(y\) 軸、頂点 \((0,2)\)
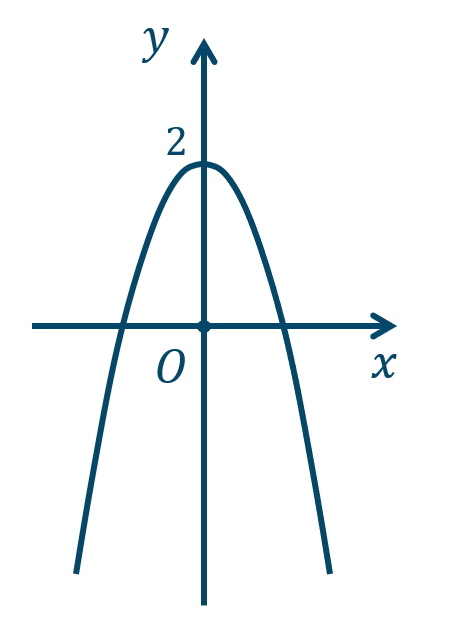
p.75
練習8
\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,0)\)

\({\small (2)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)

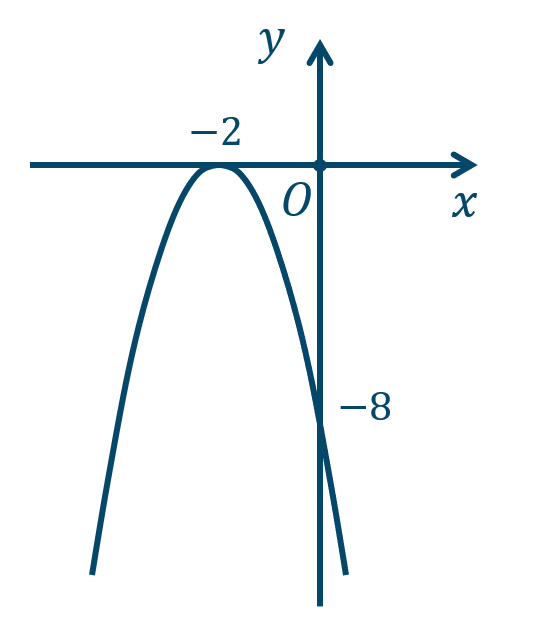
\({\small (3)}~\)軸は \(x=-2\)、頂点 \((-2,0)\)

練習8
\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,0)\)
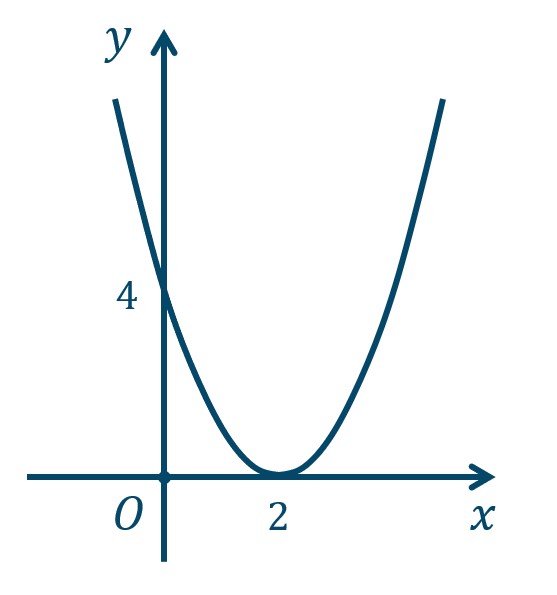
\({\small (2)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)
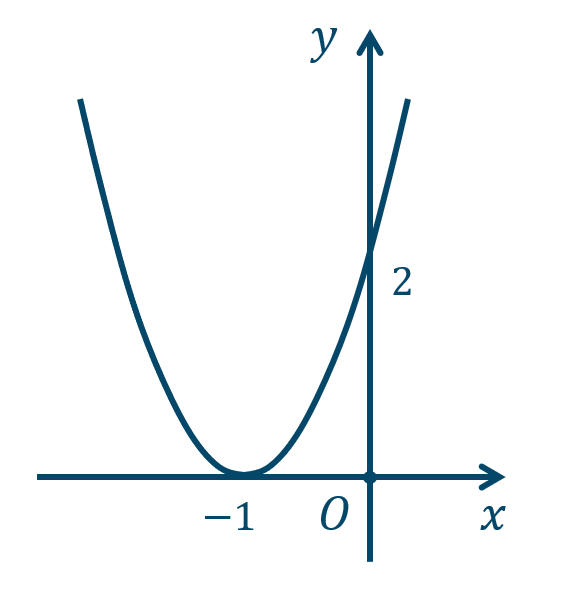
\({\small (3)}~\)軸は \(x=-2\)、頂点 \((-2,0)\)
p.76
練習9
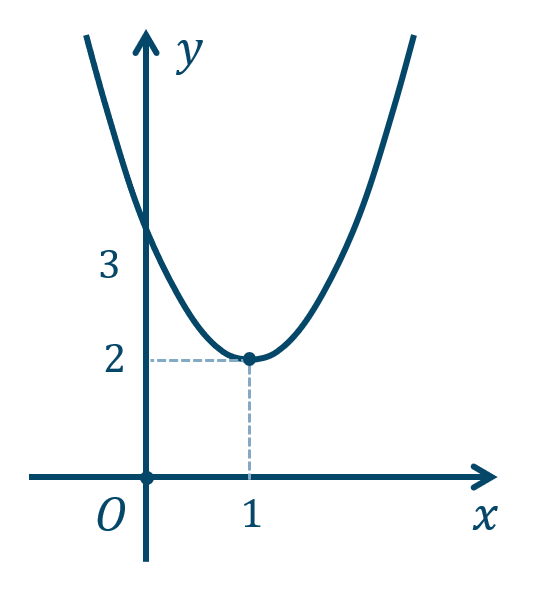
\({\small (1)}~\)軸は \(x=1\)、頂点 \((1,2)\)

\({\small (2)}~\)軸は \(x=2\)、頂点 \((2,-4)\)

\({\small (3)}~\)軸は \(x=-1\)、頂点 \((-1,2)\)

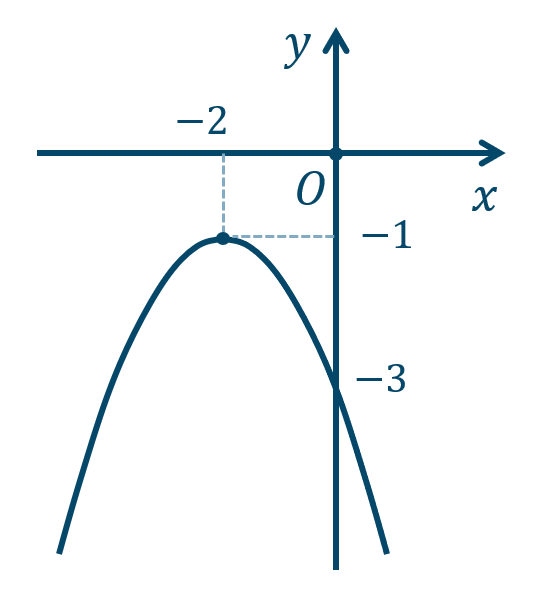
\({\small (4)}~\)軸は \(x=-2\)、頂点 \((-2,-1)\)

→ 2次関数のグラフ
練習9
\({\small (1)}~\)軸は \(x=1\)、頂点 \((1,2)\)
\({\small (2)}~\)軸は \(x=2\)、頂点 \((2,-4)\)
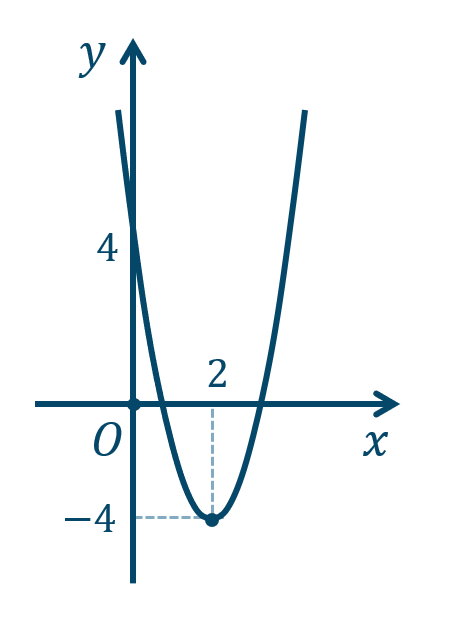
\({\small (3)}~\)軸は \(x=-1\)、頂点 \((-1,2)\)
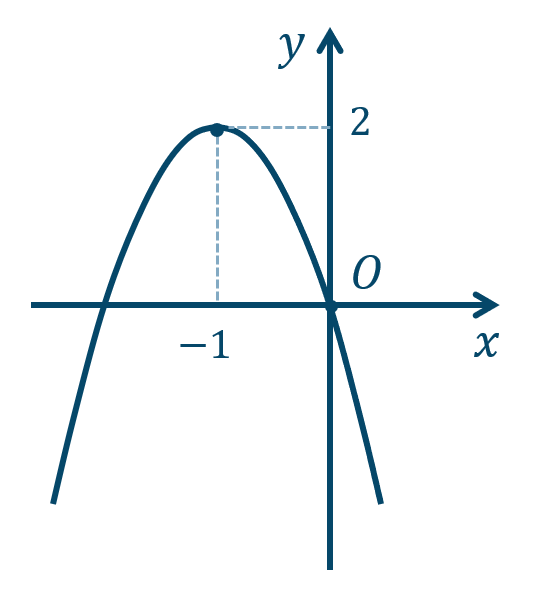
\({\small (4)}~\)軸は \(x=-2\)、頂点 \((-2,-1)\)
→ 2次関数のグラフ
p.77
練習10
\({\small (1)}~(x+4)^2-16\)
\({\small (2)}~(x-3)^2-1\)
\({\small (3)}~2(x+2)^2-3\)
\({\small (4)}~3(x+1)^2-1\)
\({\small (5)}~\left(x+{\large \frac{1}{2}}\right)^2-{\large \frac{9}{4}}\)
\({\small (6)}~-2\left(x-{\large \frac{3}{2}}\right)^2+{\large \frac{17}{2}}\)
練習10
\({\small (1)}~(x+4)^2-16\)
\({\small (2)}~(x-3)^2-1\)
\({\small (3)}~2(x+2)^2-3\)
\({\small (4)}~3(x+1)^2-1\)
\({\small (5)}~\left(x+{\large \frac{1}{2}}\right)^2-{\large \frac{9}{4}}\)
\({\small (6)}~-2\left(x-{\large \frac{3}{2}}\right)^2+{\large \frac{17}{2}}\)
p.78
練習11
\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,-1)\)

\({\small (2)}~\)軸は \(x=-2\)、頂点 \((-2,-5)\)

\({\small (3)}~\)軸は \(x=1\)、頂点 \((1,4)\)

\({\small (4)}~\)軸は \(x=-{\large \frac{3}{2}}\)、頂点 \(\left(-{\large \frac{3}{2}},{\large \frac{9}{4}}\right)\)

→ 2次関数の平方完成
練習11
\({\small (1)}~\)軸は \(x=2\)、頂点 \((2,-1)\)
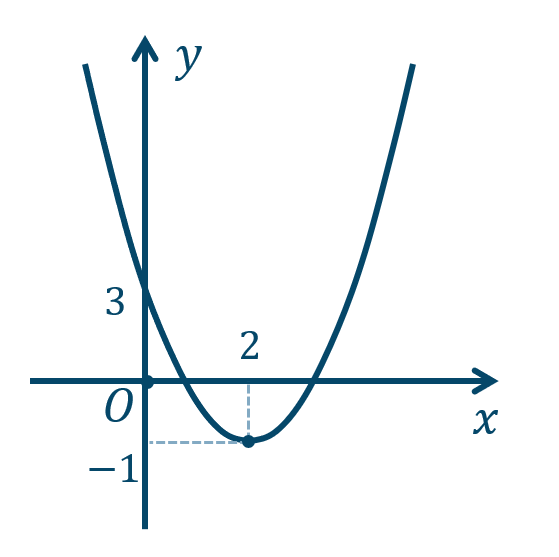
\({\small (2)}~\)軸は \(x=-2\)、頂点 \((-2,-5)\)
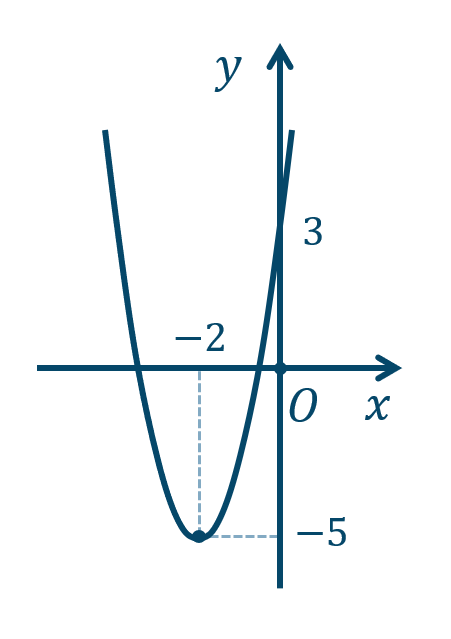
\({\small (3)}~\)軸は \(x=1\)、頂点 \((1,4)\)
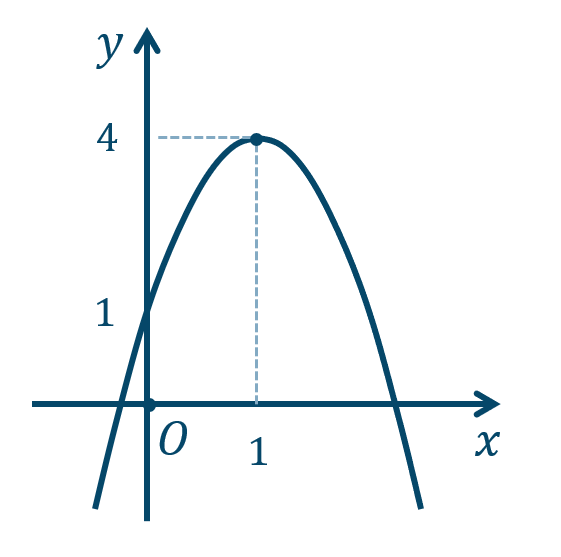
\({\small (4)}~\)軸は \(x=-{\large \frac{3}{2}}\)、頂点 \(\left(-{\large \frac{3}{2}},{\large \frac{9}{4}}\right)\)
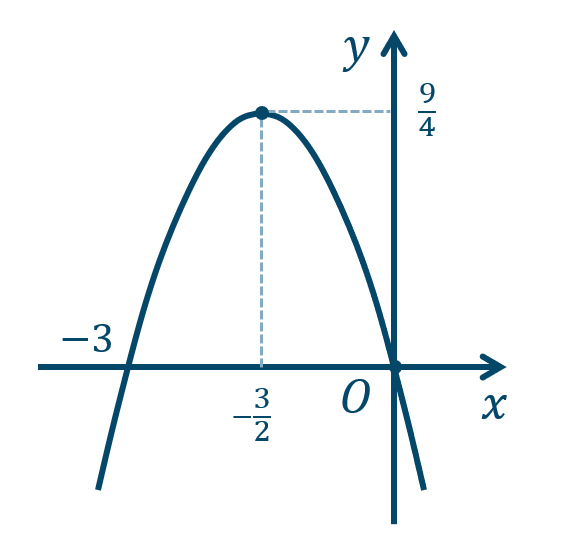
→ 2次関数の平方完成
問題
p.82
1
\({\small (1)}~0\) \({\small (2)}~-a+b\) \({\small (3)}~3a+3b\)
1
\({\small (1)}~0\) \({\small (2)}~-a+b\) \({\small (3)}~3a+3b\)
p.82
2
\(a=-2,~,~b=11\)
2
\(a=-2,~,~b=11\)
p.82
3
\({\small (1)}~y=-2(x-1)^2-3\)
\({\small (2)}~y=-2(x+2)^2+5\)
3
\({\small (1)}~y=-2(x-1)^2-3\)
\({\small (2)}~y=-2(x+2)^2+5\)
p.82
4
\({\small (1)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)

\({\small (2)}~\)軸は \(x={\large \frac{1}{2}}\)、頂点 \(\left({\large \frac{1}{2}},1\right)\)

\({\small (3)}~\)軸は \(x=3\)、頂点 \((3,-4)\)

\({\small (4)}~\)軸は \(x=-{\large \frac{5}{4}}\)、頂点 \(\left(-{\large \frac{5}{4}},-{\large \frac{49}{8}}\right)\)

4
\({\small (1)}~\)軸は \(x=-1\)、頂点 \((-1,0)\)
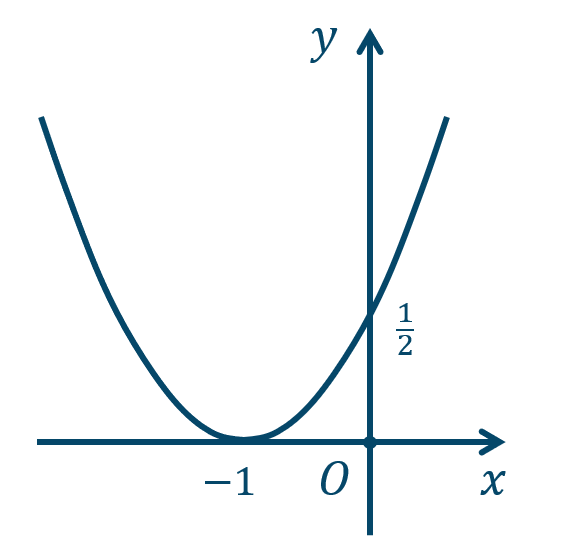
\({\small (2)}~\)軸は \(x={\large \frac{1}{2}}\)、頂点 \(\left({\large \frac{1}{2}},1\right)\)
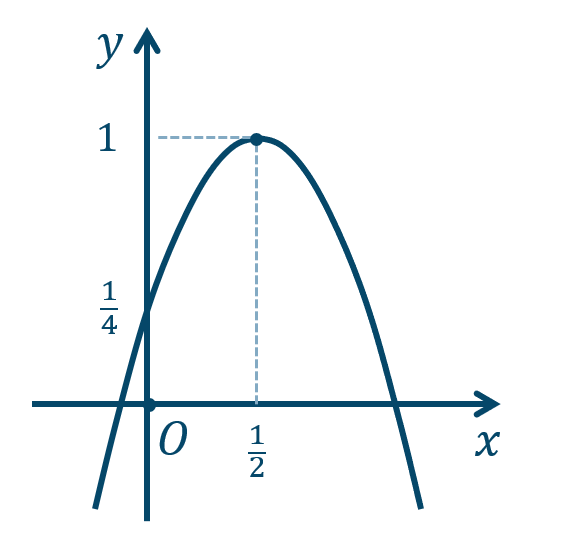
\({\small (3)}~\)軸は \(x=3\)、頂点 \((3,-4)\)
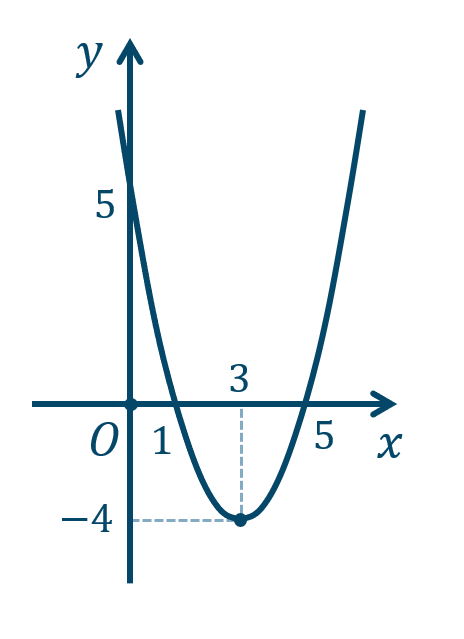
\({\small (4)}~\)軸は \(x=-{\large \frac{5}{4}}\)、頂点 \(\left(-{\large \frac{5}{4}},-{\large \frac{49}{8}}\right)\)
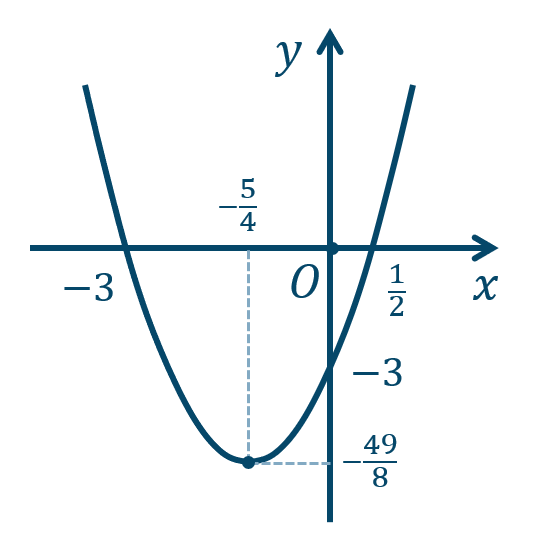
p.82
5
\({\small (1)}~(1,-3)\)
\({\small (2)}~y=2(x-3)^2-4\)
5
\({\small (1)}~(1,-3)\)
\({\small (2)}~y=2(x-3)^2-4\)
p.82
6
ア:\(6\) イ:\(1\) ウ:\(2\) エ:\(6\) オ:\(9\)
6
ア:\(6\) イ:\(1\) ウ:\(2\) エ:\(6\) オ:\(9\)
第2節 2次関数の値の変化
p.83
練習13
\({\small (1)}~\)
最大値なし
最小値 \(4~(x=3)\)
\({\small (2)}~\)
最大値 \(-3~(x=-1)\)
最小値なし
練習13
\({\small (1)}~\)
最大値なし
最小値 \(4~(x=3)\)
\({\small (2)}~\)
最大値 \(-3~(x=-1)\)
最小値なし
p.84
練習14
\({\small (1)}~\)
最大値なし
最小値 \(-4~(x=3)\)
\({\small (2)}~\)
最大値 \(5~(x=2)\)
最小値なし
\({\small (3)}~\)
最大値なし
最小値 \(-{\large \frac{5}{4}}~\left(x=-{\large \frac{3}{2}}\right)\)
\({\small (4)}~\)
最大値 \({\large \frac{25}{8}}~\left(x={\large \frac{5}{4}}\right)\)
最小値なし
練習14
\({\small (1)}~\)
最大値なし
最小値 \(-4~(x=3)\)
\({\small (2)}~\)
最大値 \(5~(x=2)\)
最小値なし
\({\small (3)}~\)
最大値なし
最小値 \(-{\large \frac{5}{4}}~\left(x=-{\large \frac{3}{2}}\right)\)
\({\small (4)}~\)
最大値 \({\large \frac{25}{8}}~\left(x={\large \frac{5}{4}}\right)\)
最小値なし
p.85
練習15
\({\small (1)}~\)
最大値 \(11~(x=2)\)
最小値 \(2~(x=-1)\)
\({\small (2)}~\)
最大値 \(1~(x=2)\)
最小値 \(-3~(x=0)\)
\({\small (3)}~\)
最大値 \(44~(x=3)\)
最小値 \(8~(x=1)\)
\({\small (4)}~\)
最大値 \(18~(x=3)\)
最小値 \(0~(x=0,6)\)
→ 2次関数の最大値・最小値
練習15
\({\small (1)}~\)
最大値 \(11~(x=2)\)
最小値 \(2~(x=-1)\)
\({\small (2)}~\)
最大値 \(1~(x=2)\)
最小値 \(-3~(x=0)\)
\({\small (3)}~\)
最大値 \(44~(x=3)\)
最小値 \(8~(x=1)\)
\({\small (4)}~\)
最大値 \(18~(x=3)\)
最小値 \(0~(x=0,6)\)
→ 2次関数の最大値・最小値
p.87
練習17
\(0<a<1\) のとき
\(x=a\) で最大値 \(-a^2+2a+1\)
\(1≦a\) のとき
\(x=1\) で最大値 \(2\)
→ 定義域が変化する2次関数の最大値・最小値
練習17
\(0<a<1\) のとき
\(x=a\) で最大値 \(-a^2+2a+1\)
\(1≦a\) のとき
\(x=1\) で最大値 \(2\)
→ 定義域が変化する2次関数の最大値・最小値
p.88
練習18
\(a<0\) のとき
\(x=0\) で最小値 \(2a^2\)
\(0≦a≦1\) のとき
\(x=a\) で最小値 \(0\)
\(1<a\) のとき
\(x=1\) で最小値 \(2a^2-4a+2\)
→ 文字係数を含む2次関数の最大値・最小値
練習18
\(a<0\) のとき
\(x=0\) で最小値 \(2a^2\)
\(0≦a≦1\) のとき
\(x=a\) で最小値 \(0\)
\(1<a\) のとき
\(x=1\) で最小値 \(2a^2-4a+2\)
→ 文字係数を含む2次関数の最大値・最小値
p.90
練習20
\({\small (1)}~y=-{\large \frac{1}{2}}(x+2)^2+4\)
\({\small (2)}~y=2(x-2)^2-13\)
→ 2次関数の決定①(頂点)
練習20
\({\small (1)}~y=-{\large \frac{1}{2}}(x+2)^2+4\)
\({\small (2)}~y=2(x-2)^2-13\)
→ 2次関数の決定①(頂点)
p.92
練習21
\({\small (1)}~a=2~,~b=-6~,~c=4\)
\({\small (2)}~x=3~,~y=2~,~z=1\)
練習21
\({\small (1)}~a=2~,~b=-6~,~c=4\)
\({\small (2)}~x=3~,~y=2~,~z=1\)
問題
p.93
7
\({\small (1)}~\)
最大値 \(-1~(x=0)\)
最小値 \(-{\large \frac{13}{4}}~\left(x={\large \frac{3}{2}}\right)\)
\({\small (2)}~\)
最大値 \({\large \frac{25}{12}}~\left(x=-{\large \frac{5}{6}}\right)\)
最小値 \(-8~(x=-1)\)
7
\({\small (1)}~\)
最大値 \(-1~(x=0)\)
最小値 \(-{\large \frac{13}{4}}~\left(x={\large \frac{3}{2}}\right)\)
\({\small (2)}~\)
最大値 \({\large \frac{25}{12}}~\left(x=-{\large \frac{5}{6}}\right)\)
最小値 \(-8~(x=-1)\)
p.93
8
\({\small (1)}~\)
\(a<0\) のとき
\(x=0\) で最小値 \(0\)
\(0≦a≦2\) のとき
\(x=a\) で最小値 \(-a^2\)
\(2<a\) のとき
\(x=2\) で最小値 \(-4a+4\)
\({\small (2)}~\)
\(a<1\) のとき
\(x=2\) で最大値 \(-4a+4\)
\(a=1\) のとき
\(x=0,2\) で最大値 \(0\)
\(1<a\) のとき
\(x=0\) で最大値 \(0\)
8
\({\small (1)}~\)
\(a<0\) のとき
\(x=0\) で最小値 \(0\)
\(0≦a≦2\) のとき
\(x=a\) で最小値 \(-a^2\)
\(2<a\) のとき
\(x=2\) で最小値 \(-4a+4\)
\({\small (2)}~\)
\(a<1\) のとき
\(x=2\) で最大値 \(-4a+4\)
\(a=1\) のとき
\(x=0,2\) で最大値 \(0\)
\(1<a\) のとき
\(x=0\) で最大値 \(0\)
p.93
9
\(8\) ㎝と \(8\) ㎝
9
\(8\) ㎝と \(8\) ㎝
p.93
10
\({\small (1)}~y=3(x+1)^2-1\)
\({\small (2)}~y=-2x^2+4x+6\)
10
\({\small (1)}~y=3(x+1)^2-1\)
\({\small (2)}~y=-2x^2+4x+6\)
p.93
11
\(y=-3(x-2)^2+8\)
11
\(y=-3(x-2)^2+8\)
p.93
12
ア:\(0\) イ:\(4\) ウ:\(1\) エ:\(0\) オ:\(1\)
カ:\(5\) キ:\(2\) ク:\(1\)
12
ア:\(0\) イ:\(4\) ウ:\(1\) エ:\(0\) オ:\(1\)
カ:\(5\) キ:\(2\) ク:\(1\)
第3節 2次方程式と2次不等式
p.94
練習23
\({\small (1)}~x=0~,~-4\)
\({\small (2)}~x=2~,~3\)
\({\small (3)}~x=-1~,~-{\large \frac{1}{2}}\)
\({\small (4)}~x=2~,~-{\large \frac{2}{3}}\)
練習23
\({\small (1)}~x=0~,~-4\)
\({\small (2)}~x=2~,~3\)
\({\small (3)}~x=-1~,~-{\large \frac{1}{2}}\)
\({\small (4)}~x=2~,~-{\large \frac{2}{3}}\)
p.95
練習24
\({\small (1)}~x={\large \frac{-7\pm\sqrt{33}}{2}}\)
\({\small (2)}~x={\large \frac{-5\pm\sqrt{37}}{6}}\)
\({\small (3)}~x=3~,~-{\large \frac{1}{3}}\)
\({\small (4)}~x=-{\large \frac{3}{2}}\)
練習24
\({\small (1)}~x={\large \frac{-7\pm\sqrt{33}}{2}}\)
\({\small (2)}~x={\large \frac{-5\pm\sqrt{37}}{6}}\)
\({\small (3)}~x=3~,~-{\large \frac{1}{3}}\)
\({\small (4)}~x=-{\large \frac{3}{2}}\)
p.96
練習25
\({\small (1)}~x=-1\pm\sqrt{3}\)
\({\small (2)}~x={\large \frac{2\pm\sqrt{10}}{3}}\)
\({\small (3)}~x=-\sqrt{3}\)
\({\small (4)}~x=\sqrt{3}\pm1\)
→ 2次方程式の解
練習25
\({\small (1)}~x=-1\pm\sqrt{3}\)
\({\small (2)}~x={\large \frac{2\pm\sqrt{10}}{3}}\)
\({\small (3)}~x=-\sqrt{3}\)
\({\small (4)}~x=\sqrt{3}\pm1\)
→ 2次方程式の解
p.98
練習27
\(m>4\)
練習27
\(m>4\)
p.100
練習29
\({\small (1)}~(-1,0)~,~(3,0)\)
\({\small (2)}~\left({\large \frac{3+\sqrt{5}}{2}},0\right)~,~\left({\large \frac{3-\sqrt{5}}{2}},0\right)\)
\({\small (3)}~(-1,0)~x\) 軸と接する
\({\small (4)}~(3,0)~,~\left(-{\large \frac{1}{2}},0\right)\)
→ 2次関数とx軸との交点
練習29
\({\small (1)}~(-1,0)~,~(3,0)\)
\({\small (2)}~\left({\large \frac{3+\sqrt{5}}{2}},0\right)~,~\left({\large \frac{3-\sqrt{5}}{2}},0\right)\)
\({\small (3)}~(-1,0)~x\) 軸と接する
\({\small (4)}~(3,0)~,~\left(-{\large \frac{1}{2}},0\right)\)
→ 2次関数とx軸との交点
p.102
練習30
\({\small (1)}~\)0個 \({\small (2)}~\)2個 \({\small (3)}~\)1個
練習30
\({\small (1)}~\)0個 \({\small (2)}~\)2個 \({\small (3)}~\)1個
p.103
発展1
\({\small (1)}~(3,1)~,~(5,5)\)
\({\small (2)}~(2,2)\)
発展1
\({\small (1)}~(3,1)~,~(5,5)\)
\({\small (2)}~(2,2)\)
p.105
練習32
\({\small (1)}~x<-2\) \({\small (2)}~x≧2\)
練習32
\({\small (1)}~x<-2\) \({\small (2)}~x≧2\)
p.107
練習33
\({\small (1)}~x<1~,~3<x\)
\({\small (2)}~-2<x<5\)
\({\small (3)}~-1≦x≦0\)
\({\small (4)}~x≦-1~,~2≦x\)
\({\small (5)}~x<-3~,~-2<x\)
\({\small (6)}~-3≦x≦3\)
→ 2次不等式の解①(因数分解)
練習33
\({\small (1)}~x<1~,~3<x\)
\({\small (2)}~-2<x<5\)
\({\small (3)}~-1≦x≦0\)
\({\small (4)}~x≦-1~,~2≦x\)
\({\small (5)}~x<-3~,~-2<x\)
\({\small (6)}~-3≦x≦3\)
→ 2次不等式の解①(因数分解)
p.108
練習34
\({\small (1)}~x≦{\large \frac{1}{2}}~,~2≦x\)
\({\small (2)}~-{\large \frac{3}{2}}<x<-1\)
\({\small (3)}~-1-\sqrt{2}≦x≦-1+\sqrt{2}\)
\({\small (4)}~x<-\sqrt{5}~,~\sqrt{5}<x\)
練習34
\({\small (1)}~x≦{\large \frac{1}{2}}~,~2≦x\)
\({\small (2)}~-{\large \frac{3}{2}}<x<-1\)
\({\small (3)}~-1-\sqrt{2}≦x≦-1+\sqrt{2}\)
\({\small (4)}~x<-\sqrt{5}~,~\sqrt{5}<x\)
p.109
練習35
\({\small (1)}~x<-{\large \frac{1}{2}}~,~1<x\)
\({\small (2)}~{\large \frac{5-\sqrt{13}}{6}}≦x≦{\large \frac{5+\sqrt{13}}{6}}\)
→ 2次不等式の解③(解の公式)
練習35
\({\small (1)}~x<-{\large \frac{1}{2}}~,~1<x\)
\({\small (2)}~{\large \frac{5-\sqrt{13}}{6}}≦x≦{\large \frac{5+\sqrt{13}}{6}}\)
→ 2次不等式の解③(解の公式)
p.109
練習36
\({\small (1)}~x=2\) 以外のすべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x=-3\)
\({\small (4)}~\)すべての実数
→ 2次不等式の解②(x軸と接する)
練習36
\({\small (1)}~x=2\) 以外のすべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x=-3\)
\({\small (4)}~\)すべての実数
→ 2次不等式の解②(x軸と接する)
p.110
練習37
\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~\)解なし
\({\small (4)}~\)すべての実数
→ 2次不等式の解④(交点がない)
練習37
\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~\)解なし
\({\small (4)}~\)すべての実数
→ 2次不等式の解④(交点がない)
p.111
練習38
\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x={\large \frac{\sqrt{3}}{3}}\)
\({\small (4)}~-1-\sqrt{3}<x<-1+\sqrt{3}\)
練習38
\({\small (1)}~\)すべての実数
\({\small (2)}~\)解なし
\({\small (3)}~x={\large \frac{\sqrt{3}}{3}}\)
\({\small (4)}~-1-\sqrt{3}<x<-1+\sqrt{3}\)
p.112
練習39
\(m≦-2\sqrt{2}~,~2\sqrt{2}≦m\)
練習39
\(m≦-2\sqrt{2}~,~2\sqrt{2}≦m\)
p.113
練習41
\({\small (1)}~3<x≦4\)
\({\small (2)}~-2≦x<-1~,~0<x≦{\large \frac{1}{3}}\)
練習41
\({\small (1)}~3<x≦4\)
\({\small (2)}~-2≦x<-1~,~0<x≦{\large \frac{1}{3}}\)
p.116
研究1
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

研究1
\({\small (1)}~\)
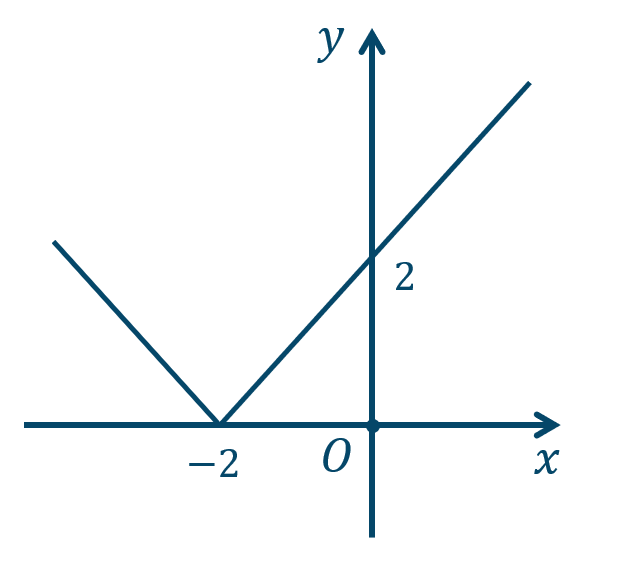
\({\small (2)}~\)
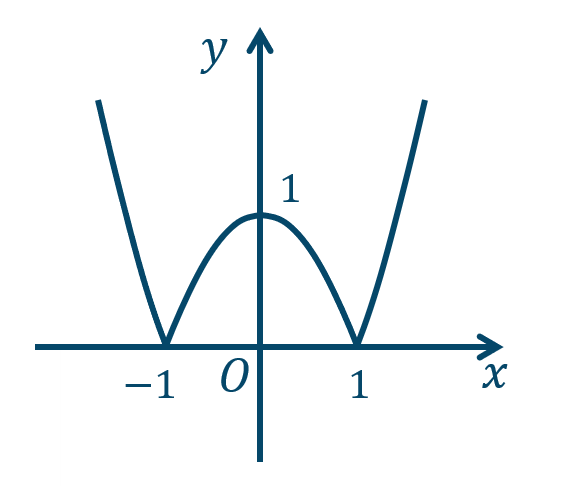
\({\small (3)}~\)
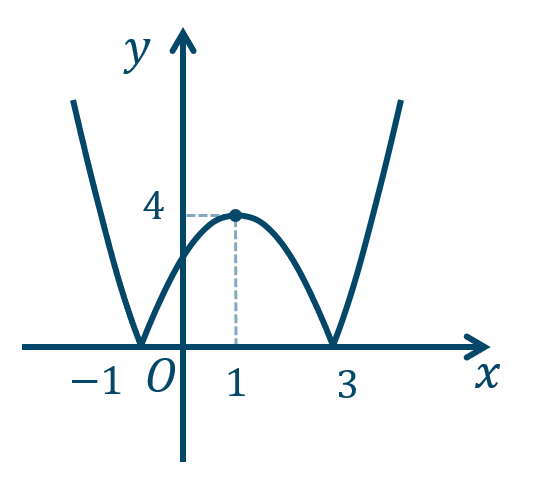
問題


