このページは、東京書籍:Standard数学Ⅱ[702]
5章 微分と積分
5章 微分と積分

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Standard数学Ⅱ 1章 方程式・式と証明
Standard数学Ⅱ 2章 図形と方程式
Standard数学Ⅱ 3章 三角関数
Standard数学Ⅱ 4章 指数関数・対数関数
Standard数学Ⅱ 5章 微分と積分
5章 微分と積分
1節 微分の考え
p.202 問1$${\small (1)}~-2+h$$$${\small (2)}~2a-4+h$$→ 平均変化率
p.203 問2$$~~~f'(1)=6~,~f'(-2)-12$$→ 微分係数
p.203 問3$$~~~-4$$
p.206 問4 \(-1≦x≦1\) の範囲で \(f'(x)≦0\)
\(1≦x≦3\) の範囲で \(f'(x)≧0\)
\(1≦x≦3\) の範囲で \(f'(x)≧0\)
p.207 問5$$~~~~~~f'(x)$$$$~=\lim_{h\to 0}{\frac{2(x+h)^2-2x^2}{h}}$$$$~=\lim_{h\to 0}{\frac{2x^2+4xh+2h^2-2x^2}{h}}$$$$~=\lim_{h\to 0}{\frac{4xh+2h^2}{h}}$$$$~=\lim_{h\to 0}(4x+2h)$$$$~=4x$$→ 導関数
p.209 問6$${\small (1)}~y’=2$$$${\small (2)}~y’=2x+4$$$${\small (3)}~y’=-6x^2-10x+7$$$${\small (4)}~y’=x^2-x-3$$
p.210 問7$${\small (1)}~y’=-8x+3$$$${\small (2)}~y’=4x-1$$$${\small (3)}~y’=8x$$$${\small (4)}~y’=3x^2+4x+1$$
p.210 問8$${\small (1)}~{ \frac{\,dh\,}{\,dt\,}}=10-10t$$$${\small (2)}~{ \frac{\,dV\,}{\,dr\,}}=4\pi r^2$$→ 微分の計算
p.210 問9$$~~~f'(1)=1~,~f'(2)=5~,~f'(-3)=-15$$
p.211 問10$$~~~a={ \frac{1}{\,2\,}}$$→ 2次関数の決定(微分係数の利用)
p.212 問11$$~~~y=5x+1$$→ 接線の方程式①
p.213 問12$$~~~y=2x~,~y=-6x-8$$→ 接線の方程式②(外部の点から引いた接線)
p.217 問13\({\small (1)}~\)\(x=-1\) で極大値 \(5\)
\(x=1\) で極小値 \(-3\)

\({\small (2)}~\)\(x=1\) で極大値 \(10\)
\(x=-3\) で極小値 \(-22\)

→ 3次関数のグラフと増減表
\(x=1\) で極小値 \(-3\)
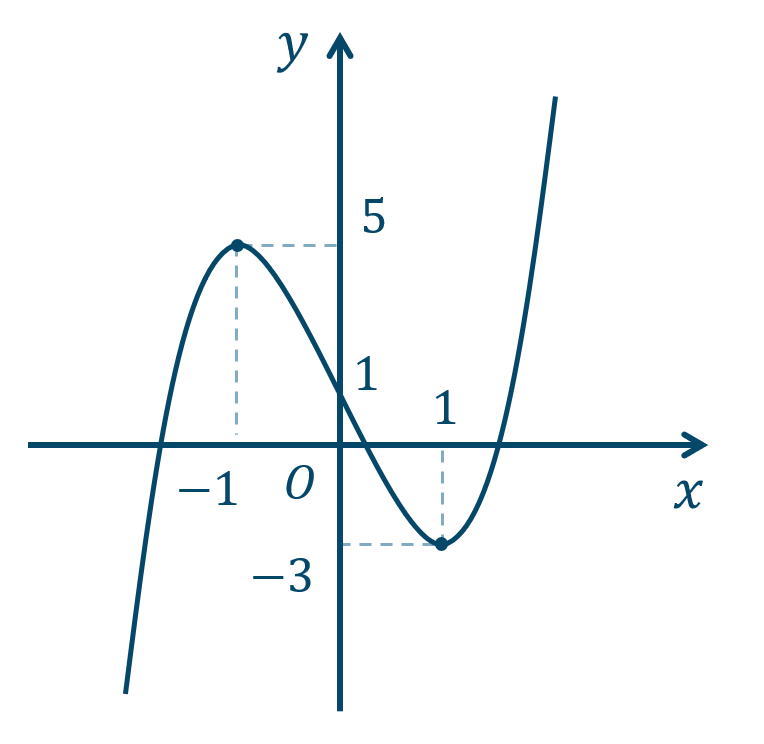
\({\small (2)}~\)\(x=1\) で極大値 \(10\)
\(x=-3\) で極小値 \(-22\)
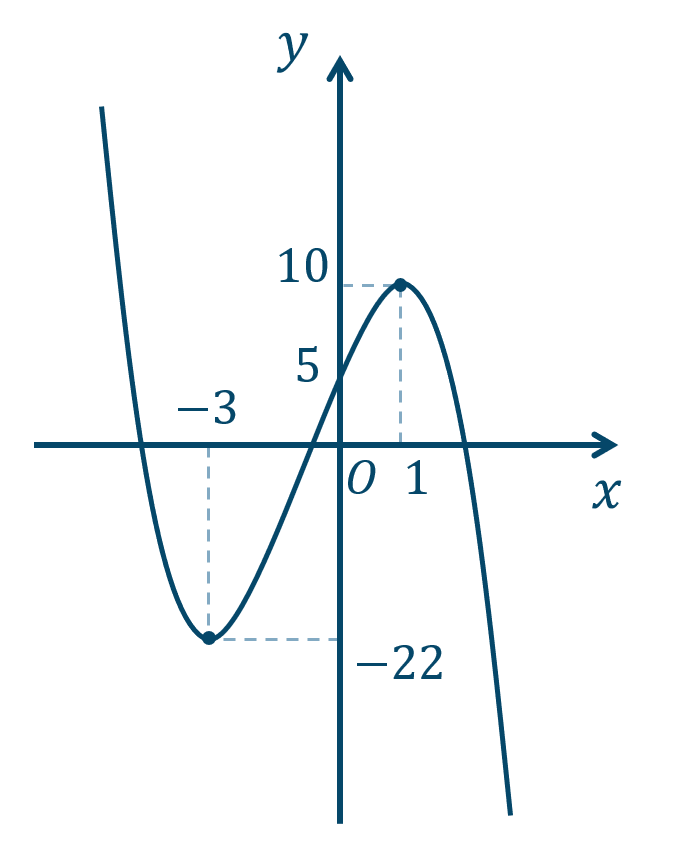
→ 3次関数のグラフと増減表
p.218 問14「\(f'(a)=0\)」は「\(f(x)\) が \(x=a\) で極値をとる」であるための、必要条件であるが十分条件でない
p.218 問15\({\small (1)}~\)極値をもたない
\({\small (2)}~\)極値をもたない
\({\small (2)}~\)極値をもたない
p.218 問16$$~~~a=-4~,~b=9$$→ 極値の条件と関数の決定
p.219 Challenge 問1\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

→ 4次関数のグラフと増減表
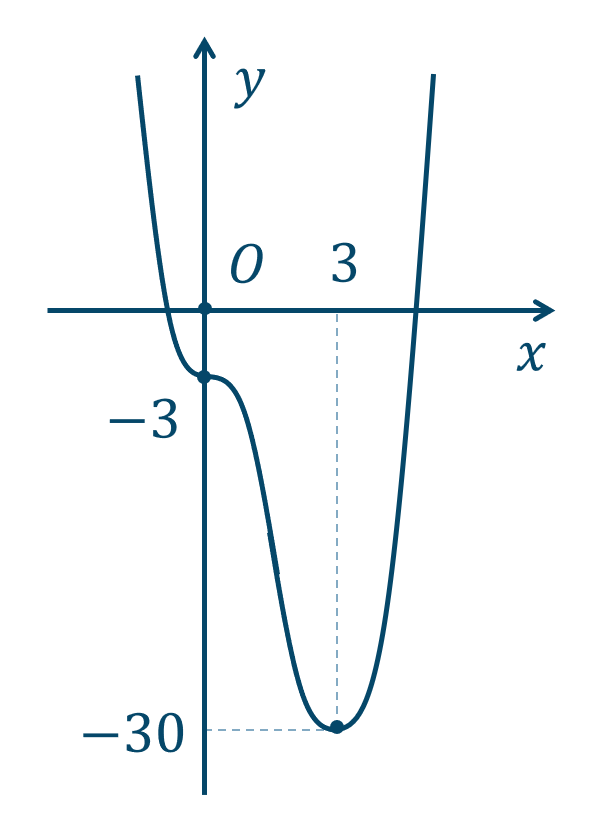
\({\small (2)}~\)
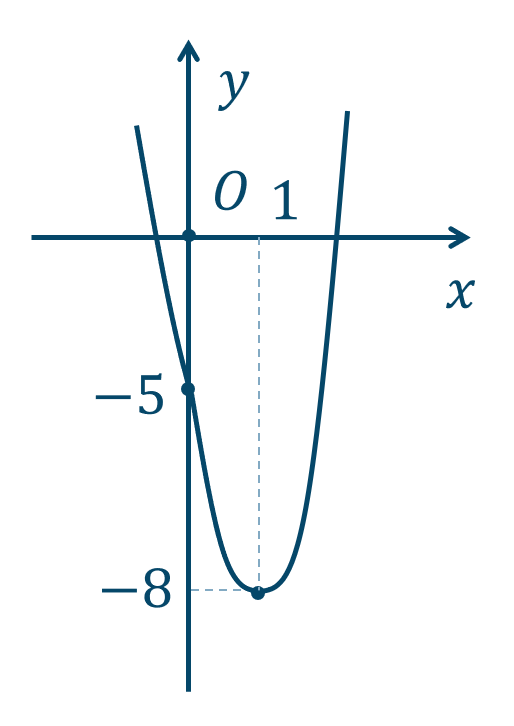
\({\small (3)}~\)
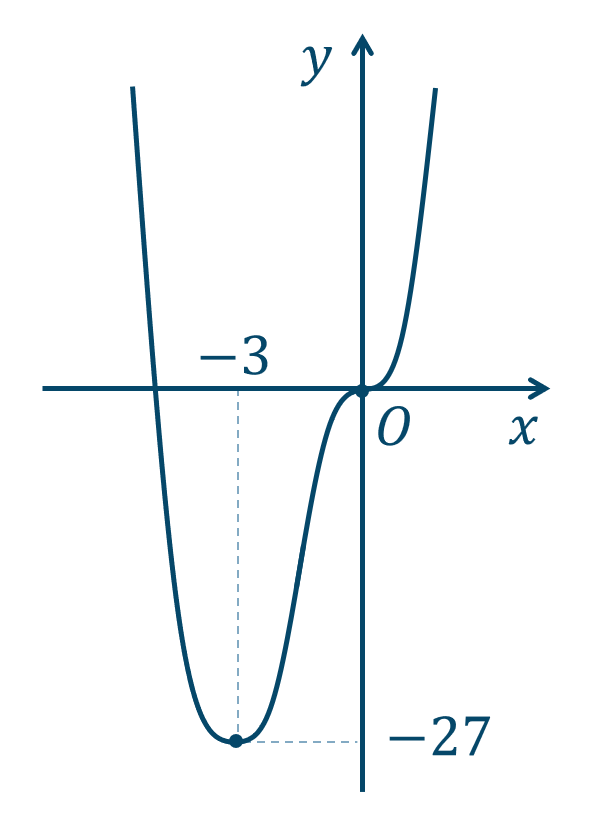
\({\small (4)}~\)
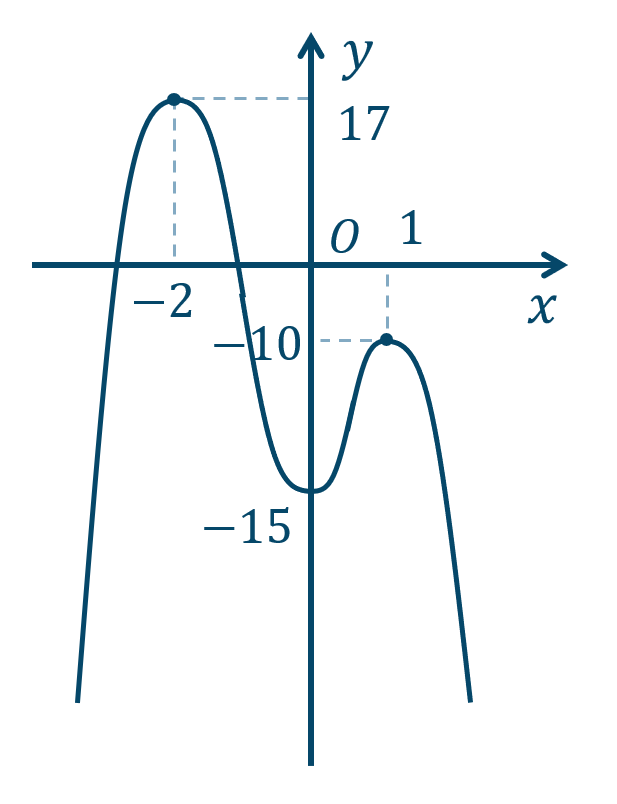
→ 4次関数のグラフと増減表
p.222 問13\({\small (1)}~\)\(x=2\) で最大値 \(12\)
\(x=-2\) で最小値 \(-4\)
\({\small (2)}~\)\(x=-2\) で最大値 \(43\)
\(x=-{\large \frac{1}{\,2\,}}\) で最小値 \(-{\large \frac{\,17\,}{4}}\)
→ 3次関数の最大値・最小値
\(x=-2\) で最小値 \(-4\)
\({\small (2)}~\)\(x=-2\) で最大値 \(43\)
\(x=-{\large \frac{1}{\,2\,}}\) で最小値 \(-{\large \frac{\,17\,}{4}}\)
→ 3次関数の最大値・最小値
p.223 問19$$~~~x=3\sqrt{3}~{\rm cm}$$
p.224 問20[証明]
\(f(x)=(x^3+16)-12x\) とすると、
\(f'(x)=3x^2-12=3(x+2)(x-2)\)
よって、\(x≧0\) での増減表は
\(f(x)=(x^3+16)-12x\) とすると、
\(f'(x)=3x^2-12=3(x+2)(x-2)\)
よって、\(x≧0\) での増減表は
| \(x\) | \(0\) | \(\cdots\) | \(2\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | |
| \(f(x)\) | \(16\) | ↘ | \(0\) | ↗ |
よって、\(x≧0\) で最小値が \(0\) であるので、
\(f(x)≧0\)
したがって、\(x≧0\) のとき
\(x^3+16≧12x\)
また、等号が成り立つときは \(x=2\) のとき [終]
→ 3次不等式の証明
Training
p.225 Training 1$${\small (1)}~10-3h$$$${\small (2)}~10$$
p.225 Training 2$$~~~~~~f'(x)$$$$~=\lim_{h\to 0}{\small \frac{3(x+h)^2+2(x+h)-(3x^2+2x)}{h}}$$$$~=\lim_{h\to 0}{\small \frac{6xh+3h^2+2h}{h}}$$$$~=\lim_{h\to 0}(6x+3h+2)$$$$~=6x+2$$
p.225 Training 3$${\small (1)}~y’=4$$$${\small (2)}~y’=-4x+3$$$${\small (3)}~y’=3x^2+6x$$$${\small (4)}~y’=-2x^2+3x-2$$$${\small (5)}~y’=12x^2+10x+18$$$${\small (6)}~y’=24x^2+72x+54$$
p.225 Training 4$${\small (1)}~f'(x)=2x+2~,~f'(-2)=-2$$$${\small (2)}~f'(x)=-3x^2+3~,~f’\left({ \frac{1}{\,2\,}}\right)={ \frac{\,9\,}{4}}$$
p.225 Training 5$$~~~a=3~,~b=5$$→ 2次関数の決定(微分係数の利用)
p.225 Training 6\({\small (1)}~\)[証明] \(y=a^2x^2+2abx+b^2\) より、微分すると、
\(y’=2a^2x+2ab=2a(ax+b)\)
したがって、
\(y=(ax+b)^2\) ならば \(y’=2a(ax+b)\) [終]
\({\small (2)}~\)[証明]
\(y=a^3x^3+3a^2bx^2+3ab^2x+b^3\) より、微分すると、
\(y’=3a^3x^2+6a^2bx+3a^2\)
\(~~=3a(a^2x^2+2abx+b^2)\)
\(~~=3a(ax+b)^2\)
したがって、
\(y=(ax+b)^3\) ならば \(y’=3a(ax+b)^2\) [終]
\(y’=2a^2x+2ab=2a(ax+b)\)
したがって、
\(y=(ax+b)^2\) ならば \(y’=2a(ax+b)\) [終]
\({\small (2)}~\)[証明]
\(y=a^3x^3+3a^2bx^2+3ab^2x+b^3\) より、微分すると、
\(y’=3a^3x^2+6a^2bx+3a^2\)
\(~~=3a(a^2x^2+2abx+b^2)\)
\(~~=3a(ax+b)^2\)
したがって、
\(y=(ax+b)^3\) ならば \(y’=3a(ax+b)^2\) [終]
p.225 Training 7$$~~~y=2x+3$$
p.225 Training 8$$~~~y=-x-1~,~y=7x-25$$
p.225 Training 9\({\small (1)}~\)
\(x≦-2\) で減少
\(-2≦x≦2\) で増加
\(x≧2\) で減少
\({\small (2)}~\)
\(x≦-1\) で増加
\(-1≦x≦2\) で減少
\(x≧2\) で増加
\(x≦-2\) で減少
\(-2≦x≦2\) で増加
\(x≧2\) で減少
\({\small (2)}~\)
\(x≦-1\) で増加
\(-1≦x≦2\) で減少
\(x≧2\) で増加
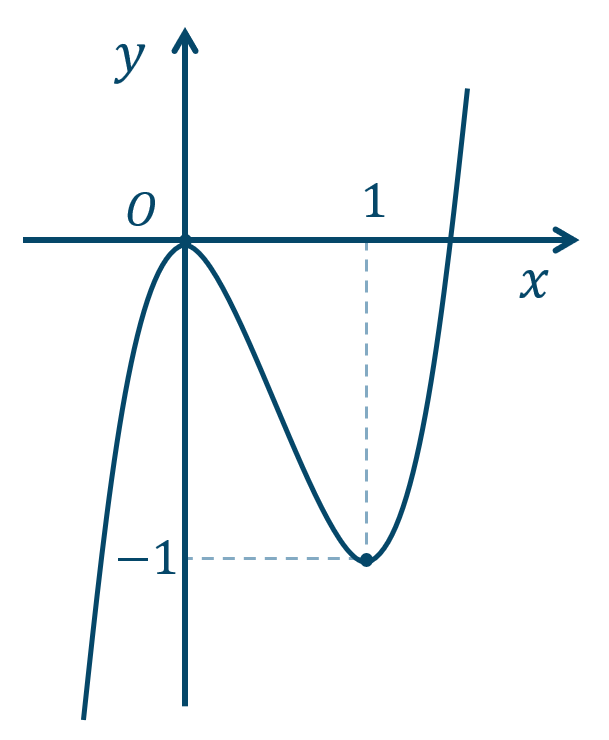
p.226 Training 10\({\small (1)}~\)\(x=0\) で極大値 \(0\)
\(x=1\) で極小値 \(-1\)

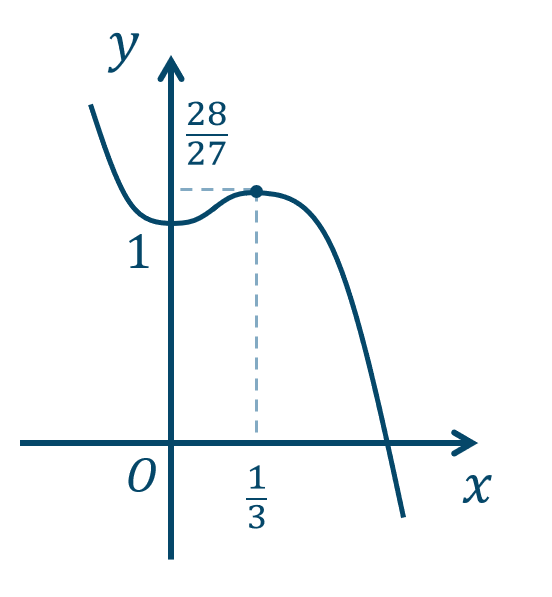
\({\small (2)}~\)\(x={\large \frac{1}{\,3\,}}\) で極大値 \({\large \frac{\,28\,}{27}}\)
\(x=0\) で極小値 \(1\)

\(x=1\) で極小値 \(-1\)
\({\small (2)}~\)\(x={\large \frac{1}{\,3\,}}\) で極大値 \({\large \frac{\,28\,}{27}}\)
\(x=0\) で極小値 \(1\)
p.226 Training 11 \(a=3~,~b=-2\)
\(x=0\) で極小値 \(-2\)
\(x=0\) で極小値 \(-2\)
p.226 Training 12\({\small (1)}~\)1個 \({\small (2)}~\)2個 \({\small (3)}~\)3個
p.226 Training 13\({\small (1)}~\)\(x=4\) で最大値 \(36\)
\(x=-1~,~2\) で最小値 \(16\)
\({\small (2)}~\)\(x=0\) で最大値 \(1\)
\(x=3\) で最小値 \(-8\)
\(x=-1~,~2\) で最小値 \(16\)
\({\small (2)}~\)\(x=0\) で最大値 \(1\)
\(x=3\) で最小値 \(-8\)
p.226 Training 14\(x=4\)
p.226 Training 15[証明]
\(f(x)=(2x^3+27)-9x^2\) とすると、
\(f'(x)=6x^2-18x=6x(x-3)\)
よって、\(x≧0\) での増減表は
\(f(x)=(2x^3+27)-9x^2\) とすると、
\(f'(x)=6x^2-18x=6x(x-3)\)
よって、\(x≧0\) での増減表は
| \(x\) | \(0\) | \(\cdots\) | \(3\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | |
| \(f(x)\) | \(27\) | ↘ | \(0\) | ↗ |
よって、\(x≧0\) で最小値が \(0\) であるので、
\(f(x)≧0\)
したがって、\(x≧0\) のとき
\(2x^3+27≧9x^2\)
また、等号が成り立つときは \(x=3\) のとき [終]
p.226 Training 16 ④
2節 積分の考え
p.228 問1$$~~~x^3+C$$\(C\) は積分定数
p.229 問2\(C\) は積分定数$${\small (1)}~3x+C$$$${\small (2)}~-2x^3+C$$$${\small (3)}~x^2+5x+C$$$${\small (4)}~{ \frac{1}{\,3\,}}x^3-2x^2-3x+C$$
p.230 問3\(C\) は積分定数$${\small (1)}~x^3+2x^2+C$$$${\small (2)}~4x^3-{ \frac{\,5\,}{2}}x^2-2x+C$$
p.230 問4\(C\) は積分定数$${\small (1)}~{ \frac{\,8\,}{3}}t^3+3t^2-9t+C$$$${\small (2)}~3t^3-6t^2+4t+C$$→ 不定積分
p.230 問5$$~~~F(x)={ \frac{1}{\,3\,}}x^3-x^2-3x+7$$→ 不定積分と関数の決定
p.232 問6$${\small (1)}~6$$$${\small (2)}~-8$$$${\small (3)}~{ \frac{\,4\,}{3}}$$$${\small (4)}~-{ \frac{1}{\,6\,}}$$
p.232 問7$${\small (1)}~-{ \frac{\,8\,}{3}}$$$${\small (2)}~2$$
p.233 問8$${\small (1)}~{ \frac{\,21\,}{2}}$$$${\small (2)}~14$$$${\small (3)}~8$$→ 定積分の計算
p.234 問9\({\small [4]}~\)[証明] \(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{a}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{a}^{a}\)
\(=F(a)-F(a)=0\)
したがって、
\(\int_{a}^{a}f(x)dx=0\) [終]
\({\small [5]}~\)[証明] \(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{b}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{b}^{a}\)
\(=F(a)-F(b)\)
\(=-\left(F(b)-F(a)\right)\)
\(=-\left[ F(x) \right]_{a}^{b}\)
\(=-\int_{a}^{b}f(x)dx\)
したがって、
\(\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx\) [終]
\(\int_{a}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{a}^{a}\)
\(=F(a)-F(a)=0\)
したがって、
\(\int_{a}^{a}f(x)dx=0\) [終]
\({\small [5]}~\)[証明] \(f(x)\)の原始関数の1つを \(F(x)\) とすると、
\(\int_{b}^{a}f(x)dx\)
\(=\left[ F(x) \right]_{b}^{a}\)
\(=F(a)-F(b)\)
\(=-\left(F(b)-F(a)\right)\)
\(=-\left[ F(x) \right]_{a}^{b}\)
\(=-\int_{a}^{b}f(x)dx\)
したがって、
\(\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx\) [終]
p.234 問10$${\small (1)}~0$$$${\small (2)}~4$$→ 定積分の計算
p.235 問11$$~~~f(x)=3x-4$$→ 定積分を含む式
p.236 問12\({\small (1)}~\)関数 \(f(x)\) は \(4x^2-x+2\) の原始関数であり、関数 \(f(x)\) の導関数は \(4x^2-x+2\) である$${\small (2)}~4x^2-x+2$$→ 定積分で表された関数
p.236 問13$$~~~f(x)=2x-5~,~a=3$$→ 定積分で表された関数
p.240 問14$$~~~{ \frac{\,68\,}{3}}$$
p.242 問15$${\small (1)}~{ \frac{1}{\,6\,}}$$$${\small (2)}~{ \frac{\,9\,}{2}}$$→ 定積分と面積①(x軸と囲まれた面積)
p.244 問16$$~~~{ \frac{\,52\,}{3}}$$→ 定積分と面積③(区間付きの面積)
p.244 問17$$~~~{ \frac{\,4\,}{3}}$$→ 定積分と面積②(2つの関数で囲まれた面積)
p.245 問18$$~~~{ \frac{\,22\,}{3}}$$→ 絶対値を含む関数の定積分
p.246 Challenge 問1$$~~~{ \frac{1}{\,2\,}}$$
Training
p.247 Training 17\(C\) は積分定数$${\small (1)}~5x+C$$$${\small (2)}~-3y^3+C$$$${\small (3)}~2x^2-6x+C$$$${\small (4)}~-{ \frac{2}{\,3\,}}x^3+{ \frac{\,3\,}{2}}x^2-4x+C$$
p.247 Training 18\(C\) は積分定数$${\small (1)}~{ \frac{\,4\,}{3}}x^3+2x^2+x+C$$$${\small (2)}~x^3-{ \frac{1}{\,2\,}}x^2-2x+C$$
p.247 Training 19$$~~~F(x)=-2x^3+4x^2+3x-5$$
p.247 Training 20$${\small (1)}~{ \frac{2}{\,3\,}}$$$${\small (2)}~{ \frac{\,3\,}{2}}$$$${\small (3)}~2$$$${\small (4)}~112$$
p.247 Training 21$$~~~6$$
p.247 Training 22$$~~~f(x)=2x-{ \frac{\,125\,}{24}}$$
p.247 Training 23$$~~~f(x)=12x+9~,~a=-3$$
p.247 Training 24$$~~~f(x)=6x+2~,~a=1~,~-{ \frac{\,5\,}{3}}$$
p.247 Training 25$$~~~12$$
p.247 Training 26$$~~~{ \frac{\,4\,}{3}}$$
p.247 Training 27$$~~~{ \frac{\,125\,}{3}}$$
p.247 Training 28$$~~~1$$
p.247 Training 29成り立たない
\(f(x)=x\) のとき、
左辺は、$$~~~\int_{a}^{x}\frac{\,d\,}{\,dt\,}t\,dt=\int_{a}^{x}1\,dt=\left[ t \right]_{a}^{x}=x-a$$右辺の \(x\) と一致しない
\(f(x)=x\) のとき、
左辺は、$$~~~\int_{a}^{x}\frac{\,d\,}{\,dt\,}t\,dt=\int_{a}^{x}1\,dt=\left[ t \right]_{a}^{x}=x-a$$右辺の \(x\) と一致しない
Level Up 微分と積分
p.248 Level Up 1$$~~~a=4$$
p.248 Level Up 2$$~~~a=2~,~b=-2$$
p.248 Level Up 3$${\small (1)}~y=-3x-3$$$${\small (2)}~y=9x+25~,~y=9x-7$$
p.248 Level Up 4$$~~~a>2$$
p.248 Level Up 5\({\small (1)}~\)\(x=1\) で極大値 \(4\)
\(x=3\) で極小値 \(0\)
\({\small (2)}~\)
\(0<a<1\) のとき
\(x=a\) で最大値 \(a(a-3)^2\)
\(1≦a<4\) のとき
\(x=1\) で最大値 \(4\)
\(a=4\) のとき
\(x=1~,~4\) で最大値 \(4\)
\(a>4\) のとき
\(x=a\) で最大値 \(a(a-3)^2\)
\(x=3\) で極小値 \(0\)
\({\small (2)}~\)
\(0<a<1\) のとき
\(x=a\) で最大値 \(a(a-3)^2\)
\(1≦a<4\) のとき
\(x=1\) で最大値 \(4\)
\(a=4\) のとき
\(x=1~,~4\) で最大値 \(4\)
\(a>4\) のとき
\(x=a\) で最大値 \(a(a-3)^2\)
p.248 Level Up 6$$~~~a>27$$
p.249 Level Up 7$$~~~f(x)=x^3-2x^2+6$$
p.249 Level Up 8$$~~~f(x)=x^2-{ \frac{\,8\,}{3}}x$$
p.249 Level Up 9 \(x=0\) で極大値 \(0\)
\(x=2\) で極小値 \(-4\)
\(x=2\) で極小値 \(-4\)
p.249 Level Up 10$$~~~{ \frac{\,27\,}{4}}$$
p.249 Level Up 11$${\small (1)}~y=6x+7~,~y=-2x+7$$$${\small (2)}~{ \frac{\,16\,}{3}}$$
p.249 Level Up 12$$~~~S_1=\frac{\,1\,}{\,6\,}~,~S_2=\frac{\,1\,}{\,3\,}~,~S_1:S_2=1:2$$
p.249 Level Up 13\(a≦0\) のとき$$~~~f(a)=-3a+{ \frac{\,9\,}{2}}$$\(0<a<3\) のとき$$~~~f(a)=a^2-3a+{ \frac{\,9\,}{2}}$$\(a≧3\) のとき$$~~~f(a)=3a-{ \frac{\,9\,}{2}}$$
p.252 参考 問1$$~~~{ \frac{\,32\,}{3}}$$


