文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 平面上のベクトル
第1節 ベクトルとその演算
p.7 練習1
\({\small (1)}~\)①と⑧、③と⑤と⑥
\({\small (2)}~\)①と⑧、②と⑦、③と④
\({\small (3)}~\)①と⑧
\({\small (4)}~\)⑤と⑥
→ ベクトルの基本
\({\small (1)}~\)①と⑧、③と⑤と⑥
\({\small (2)}~\)①と⑧、②と⑦、③と④
\({\small (3)}~\)①と⑧
\({\small (4)}~\)⑤と⑥
→ ベクトルの基本
p.9 練習3
[証明] \(\overrightarrow{\rm AB}+\overrightarrow{\rm BD}+\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BD})+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AD}+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm CA}+\overrightarrow{\rm AD}\)
\(=\overrightarrow{\rm CD}\) [終]
[証明] \(\overrightarrow{\rm AB}+\overrightarrow{\rm BD}+\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BD})+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AD}+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm CA}+\overrightarrow{\rm AD}\)
\(=\overrightarrow{\rm CD}\) [終]
p.10 練習4
[証明] \(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AC}+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AA}\)
\(=\overrightarrow{0}\) [終]
→ ベクトルの等式証明
[証明] \(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AC}+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AA}\)
\(=\overrightarrow{0}\) [終]
→ ベクトルの等式証明
p.11 練習6
\({\small (1)}~{\large \frac{1}{3}}\) \({\small (2)}~{\large \frac{3}{2}}\) \({\small (3)}~-{\large \frac{2}{3}}\)
→ ベクトルの実数倍・加法・減法
\({\small (1)}~{\large \frac{1}{3}}\) \({\small (2)}~{\large \frac{3}{2}}\) \({\small (3)}~-{\large \frac{2}{3}}\)
→ ベクトルの実数倍・加法・減法
p.11 練習7
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

\({\small (1)}~\)
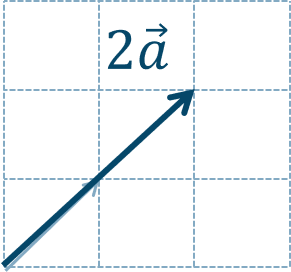
\({\small (2)}~\)
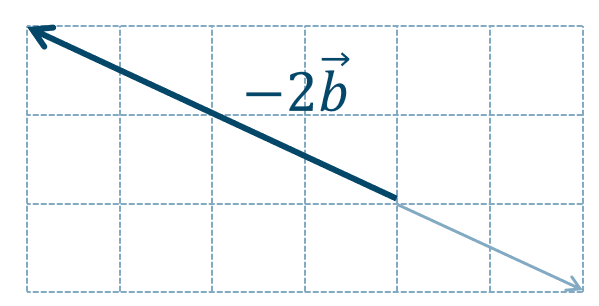
\({\small (3)}~\)
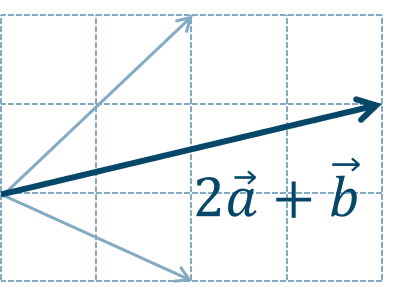
\({\small (4)}~\)
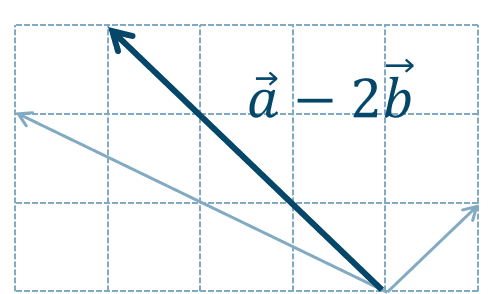
p.12 練習8
\({\small (1)}~2\overrightarrow{a}\) \({\small (2)}~-2\overrightarrow{a}+5\overrightarrow{b}\)
\({\small (3)}~10\overrightarrow{a}-5\overrightarrow{b}\) \({\small (4)}~-7\overrightarrow{a}\)
→ ベクトルの演算
\({\small (1)}~2\overrightarrow{a}\) \({\small (2)}~-2\overrightarrow{a}+5\overrightarrow{b}\)
\({\small (3)}~10\overrightarrow{a}-5\overrightarrow{b}\) \({\small (4)}~-7\overrightarrow{a}\)
→ ベクトルの演算
p.13 練習9
\({\small (1)}~4\overrightarrow{e}~,~-4\overrightarrow{e}\)
\({\small (2)}~{\large \frac{1}{3}}\overrightarrow{a}\)
\({\small (1)}~4\overrightarrow{e}~,~-4\overrightarrow{e}\)
\({\small (2)}~{\large \frac{1}{3}}\overrightarrow{a}\)
p.14 練習10
\({\small (1)}~2\overrightarrow{a}+\overrightarrow{b}\)
\({\small (2)}~-\overrightarrow{a}-\overrightarrow{b}\)
\({\small (3)}~-\overrightarrow{a}-2\overrightarrow{b}\)
→ ベクトルの分解(正六角形のベクトル)
\({\small (1)}~2\overrightarrow{a}+\overrightarrow{b}\)
\({\small (2)}~-\overrightarrow{a}-\overrightarrow{b}\)
\({\small (3)}~-\overrightarrow{a}-2\overrightarrow{b}\)
→ ベクトルの分解(正六角形のベクトル)
p.16 練習11
\(\overrightarrow{b}=(-2,4)~,~|\overrightarrow{b}|=2\sqrt{5}\)
\(\overrightarrow{c}=(-2,-2)~,~|\overrightarrow{c}|=2\sqrt{2}\)
\(\overrightarrow{d}=(3,-4)~,~|\overrightarrow{d}|=5\)
\(\overrightarrow{e}=(-1,0)~,~|\overrightarrow{e}|=1\)
→ ベクトルの成分と大きさ
\(\overrightarrow{b}=(-2,4)~,~|\overrightarrow{b}|=2\sqrt{5}\)
\(\overrightarrow{c}=(-2,-2)~,~|\overrightarrow{c}|=2\sqrt{2}\)
\(\overrightarrow{d}=(3,-4)~,~|\overrightarrow{d}|=5\)
\(\overrightarrow{e}=(-1,0)~,~|\overrightarrow{e}|=1\)
→ ベクトルの成分と大きさ
p.17 練習12
\({\small (1)}~(6,-2)\)
\({\small (2)}~(4,-2)\)
\({\small (3)}~\left(-1,{\large \frac{1}{2}}\right)\)
\({\small (4)}~(1,1)\)
\({\small (5)}~(24,-10)\)
\({\small (6)}~(-26,10)\)
\({\small (1)}~(6,-2)\)
\({\small (2)}~(4,-2)\)
\({\small (3)}~\left(-1,{\large \frac{1}{2}}\right)\)
\({\small (4)}~(1,1)\)
\({\small (5)}~(24,-10)\)
\({\small (6)}~(-26,10)\)
p.19 練習15
\({\small (1)}~\overrightarrow{\rm AB}=(-4,4)~,~|\overrightarrow{\rm AB}|=4\sqrt{2}\)
\({\small (2)}~\overrightarrow{\rm AB}=(5,-4)~,~|\overrightarrow{\rm AB}|=\sqrt{41}\)
→ 点の座標とベクトルの成分
\({\small (1)}~\overrightarrow{\rm AB}=(-4,4)~,~|\overrightarrow{\rm AB}|=4\sqrt{2}\)
\({\small (2)}~\overrightarrow{\rm AB}=(5,-4)~,~|\overrightarrow{\rm AB}|=\sqrt{41}\)
→ 点の座標とベクトルの成分
p.21 練習17
\({\small (1)}~6\sqrt{2}\) \({\small (2)}~-18\sqrt{3}\)
\({\small (1)}~6\sqrt{2}\) \({\small (2)}~-18\sqrt{3}\)
p.23 練習20
\({\small (1)}~135^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~90^\circ\) \({\small (4)}~180^\circ\)
\({\small (5)}~0^\circ\)
→ ベクトルのなす角
\({\small (1)}~135^\circ\) \({\small (2)}~30^\circ\)
\({\small (3)}~90^\circ\) \({\small (4)}~180^\circ\)
\({\small (5)}~0^\circ\)
→ ベクトルのなす角
p.23 練習21
\(x=-1~,~2\)
\(x=-1~,~2\)
p.24 練習22
\({\small (1)}~\)
\(\overrightarrow{b}=(\sqrt{2},-2\sqrt{2})~,~(-\sqrt{2},2\sqrt{2})\)
\({\small (2)}~\)
\(\overrightarrow{e}=\left({\large \frac{3}{5}},-{\large \frac{4}{5}}\right)~,~\left(-{\large \frac{3}{5}},{\large \frac{4}{5}}\right)\)
→ ベクトルの垂直条件
\({\small (1)}~\)
\(\overrightarrow{b}=(\sqrt{2},-2\sqrt{2})~,~(-\sqrt{2},2\sqrt{2})\)
\({\small (2)}~\)
\(\overrightarrow{e}=\left({\large \frac{3}{5}},-{\large \frac{4}{5}}\right)~,~\left(-{\large \frac{3}{5}},{\large \frac{4}{5}}\right)\)
→ ベクトルの垂直条件
p.24 練習23
\((-2,-4)\)
\((-2,-4)\)
p.25 練習24
[証明]
\(\overrightarrow{a}=(a_1,a_2)\)
\(\overrightarrow{b}=(b_1,b_2)\)
\(\overrightarrow{c}=(c_1,c_2)\)
とすると、
\(\overrightarrow{b}-\overrightarrow{c}=(b_1-c_1,b_2-c_2)\)
となる
(左辺)
\(=\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})\)
\(=a_1(b_1-c_1)+a_2(b_2-c_2)\)
\(=a_1b_1+a_2b_2-a_1c_1-a_2c_2\)
(右辺)
\(=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\)
\(=(a_1b_1+a_2b_2)-(a_1c_1+a_2c_2)\)
したがって、
\(\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\)
[終]
[証明]
\(\overrightarrow{a}=(a_1,a_2)\)
\(\overrightarrow{b}=(b_1,b_2)\)
\(\overrightarrow{c}=(c_1,c_2)\)
とすると、
\(\overrightarrow{b}-\overrightarrow{c}=(b_1-c_1,b_2-c_2)\)
となる
(左辺)
\(=\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})\)
\(=a_1(b_1-c_1)+a_2(b_2-c_2)\)
\(=a_1b_1+a_2b_2-a_1c_1-a_2c_2\)
(右辺)
\(=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\)
\(=(a_1b_1+a_2b_2)-(a_1c_1+a_2c_2)\)
したがって、
\(\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\)
[終]
p.26 練習25
\({\small (1)}~\)[証明]
(左辺)
\(=|2\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=(2\overrightarrow{a}+\overrightarrow{b})\cdot(2\overrightarrow{a}+\overrightarrow{b})\)
\(=2\overrightarrow{a}\cdot(2\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{b}(2\overrightarrow{a}+\overrightarrow{b})\)
\(=2\overrightarrow{a}\cdot2\overrightarrow{a}+2\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+2\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=4|\overrightarrow{a}|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\(|2\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=4|\overrightarrow{a}|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
[終]
\({\small (2)}~\)[証明]
(左辺)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+\overrightarrow{b}\cdot\overrightarrow{a}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\((\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
[終]
→ 内積を用いた等式証明
\({\small (1)}~\)[証明]
(左辺)
\(=|2\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=(2\overrightarrow{a}+\overrightarrow{b})\cdot(2\overrightarrow{a}+\overrightarrow{b})\)
\(=2\overrightarrow{a}\cdot(2\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{b}(2\overrightarrow{a}+\overrightarrow{b})\)
\(=2\overrightarrow{a}\cdot2\overrightarrow{a}+2\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+2\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=4|\overrightarrow{a}|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\(|2\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=4|\overrightarrow{a}|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
[終]
\({\small (2)}~\)[証明]
(左辺)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+\overrightarrow{b}\cdot\overrightarrow{a}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\((\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
[終]
→ 内積を用いた等式証明
p.27 研究1
\(5\sqrt{3}\)
\(5\sqrt{3}\)
補充問題
p.28 1
\({\small (1)}~\overrightarrow{x}=2\overrightarrow{a}-\overrightarrow{b}\)
\({\small (2)}~\overrightarrow{x}=-2\overrightarrow{a}-{\large \frac{10}{3}}\overrightarrow{b}\)
\({\small (1)}~\overrightarrow{x}=2\overrightarrow{a}-\overrightarrow{b}\)
\({\small (2)}~\overrightarrow{x}=-2\overrightarrow{a}-{\large \frac{10}{3}}\overrightarrow{b}\)
p.28 2
\({\small (1)}~\)[証明]
ベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) のなす角を \(\theta\) とすると、
\(\overrightarrow{a}\parallel\overrightarrow{b}\)
\(~\Leftrightarrow~\theta=0^\circ\) または \(\theta=180^\circ\)
\(~\Leftrightarrow~\cos{\theta}=1\) または \(\cos{\theta}=-1\)
\(~\Leftrightarrow~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\) または \(\overrightarrow{a}\cdot\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)
よって、\(|\overrightarrow{a}\cdot\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|\)
\(|\overrightarrow{a}\cdot\overrightarrow{b}|≧0~,~|\overrightarrow{a}|≧0~,~|\overrightarrow{b}|≧0\) であるので、
\(|\overrightarrow{a}\cdot\overrightarrow{b}|^2=|\overrightarrow{a}|^2|\overrightarrow{b}|^2\)
それぞれの成分より、
\((a_1b_1+a_2b_2)^2\)
\(=(a_1^2+a_2^2)(b_1^2+b_2^2)\)
展開して計算すると、
\((a_1b_2-a_2b_1)^2=0\)
よって、
\(a_1b_2-a_2b_1=0\)
したがって、\(\overrightarrow{a}\neq\overrightarrow{0}~,~\overrightarrow{b}\neq\overrightarrow{0}\) で、
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) のとき、
\(\overrightarrow{a}\parallel\overrightarrow{b}~\Leftrightarrow~a_1b_2-a_2b_1=0\)
[終]
\({\small (2)}~x=-3\)
\({\small (1)}~\)[証明]
ベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) のなす角を \(\theta\) とすると、
\(\overrightarrow{a}\parallel\overrightarrow{b}\)
\(~\Leftrightarrow~\theta=0^\circ\) または \(\theta=180^\circ\)
\(~\Leftrightarrow~\cos{\theta}=1\) または \(\cos{\theta}=-1\)
\(~\Leftrightarrow~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\) または \(\overrightarrow{a}\cdot\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)
よって、\(|\overrightarrow{a}\cdot\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|\)
\(|\overrightarrow{a}\cdot\overrightarrow{b}|≧0~,~|\overrightarrow{a}|≧0~,~|\overrightarrow{b}|≧0\) であるので、
\(|\overrightarrow{a}\cdot\overrightarrow{b}|^2=|\overrightarrow{a}|^2|\overrightarrow{b}|^2\)
それぞれの成分より、
\((a_1b_1+a_2b_2)^2\)
\(=(a_1^2+a_2^2)(b_1^2+b_2^2)\)
展開して計算すると、
\((a_1b_2-a_2b_1)^2=0\)
よって、
\(a_1b_2-a_2b_1=0\)
したがって、\(\overrightarrow{a}\neq\overrightarrow{0}~,~\overrightarrow{b}\neq\overrightarrow{0}\) で、
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) のとき、
\(\overrightarrow{a}\parallel\overrightarrow{b}~\Leftrightarrow~a_1b_2-a_2b_1=0\)
[終]
\({\small (2)}~x=-3\)
p.28 3
\({\small (1)}~-{\large \frac{3}{2}}\) \({\small (2)}~\theta=150^\circ\)
\({\small (1)}~-{\large \frac{3}{2}}\) \({\small (2)}~\theta=150^\circ\)
第2節 ベクトルと平面図形
p.29 練習27
\({\small (1)}~\overrightarrow{c}-\overrightarrow{b}\)
\({\small (2)}~\overrightarrow{a}-\overrightarrow{c}\)
\({\small (3)}~\overrightarrow{a}-\overrightarrow{b}\)
\({\small (1)}~\overrightarrow{c}-\overrightarrow{b}\)
\({\small (2)}~\overrightarrow{a}-\overrightarrow{c}\)
\({\small (3)}~\overrightarrow{a}-\overrightarrow{b}\)
p.31 練習28
\({\small (1)}~{\large \frac{3}{5}}\overrightarrow{a}+{\large \frac{2}{5}}\overrightarrow{b}\)
\({\small (2)}~{\large \frac{1}{4}}\overrightarrow{a}+{\large \frac{3}{4}}\overrightarrow{b}\)
\({\small (3)}~-{\large \frac{1}{3}}\overrightarrow{a}+{\large \frac{4}{3}}\overrightarrow{b}\)
\({\small (4)}~2\overrightarrow{a}-\overrightarrow{b}\)
→ 内分点・外分点の位置ベクトル
\({\small (1)}~{\large \frac{3}{5}}\overrightarrow{a}+{\large \frac{2}{5}}\overrightarrow{b}\)
\({\small (2)}~{\large \frac{1}{4}}\overrightarrow{a}+{\large \frac{3}{4}}\overrightarrow{b}\)
\({\small (3)}~-{\large \frac{1}{3}}\overrightarrow{a}+{\large \frac{4}{3}}\overrightarrow{b}\)
\({\small (4)}~2\overrightarrow{a}-\overrightarrow{b}\)
→ 内分点・外分点の位置ベクトル
p.33 練習29
\({\small (1)}~\overrightarrow{g}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
\({\small (2)}~\)[証明] \({\rm G}\) の位置ベクトルが
\(\overrightarrow{g}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
であるので、
\(\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}\)
\(=(\overrightarrow{a}-\overrightarrow{g})+(\overrightarrow{b}-\overrightarrow{g})+(\overrightarrow{c}-\overrightarrow{g})\)
\(=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{g}\)
\(=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\left({\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\right)\)
\(=\overrightarrow{0}\)
したがって、
\(\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}\) [終]
→ 重心の位置ベクトル
\({\small (1)}~\overrightarrow{g}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
\({\small (2)}~\)[証明] \({\rm G}\) の位置ベクトルが
\(\overrightarrow{g}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
であるので、
\(\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}\)
\(=(\overrightarrow{a}-\overrightarrow{g})+(\overrightarrow{b}-\overrightarrow{g})+(\overrightarrow{c}-\overrightarrow{g})\)
\(=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{g}\)
\(=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\left({\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\right)\)
\(=\overrightarrow{0}\)
したがって、
\(\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}\) [終]
→ 重心の位置ベクトル
p.34 練習30
\({\small (1)}~\overrightarrow{\rm AE}={\large \frac{1}{3}}\overrightarrow{\rm AB}+{\large \frac{2}{3}}\overrightarrow{\rm AC}\)
\({\small (2)}~\overrightarrow{\rm AF}=-2\overrightarrow{\rm AB}+3\overrightarrow{\rm AC}\)
\({\small (3)}~\overrightarrow{\rm EF}=-{\large \frac{7}{3}}\overrightarrow{\rm AB}+{\large \frac{7}{3}}\overrightarrow{\rm AC}\)
→ 内分点・外分点の位置ベクトル
\({\small (1)}~\overrightarrow{\rm AE}={\large \frac{1}{3}}\overrightarrow{\rm AB}+{\large \frac{2}{3}}\overrightarrow{\rm AC}\)
\({\small (2)}~\overrightarrow{\rm AF}=-2\overrightarrow{\rm AB}+3\overrightarrow{\rm AC}\)
\({\small (3)}~\overrightarrow{\rm EF}=-{\large \frac{7}{3}}\overrightarrow{\rm AB}+{\large \frac{7}{3}}\overrightarrow{\rm AC}\)
→ 内分点・外分点の位置ベクトル
p.35 練習31
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とすると
点 \({\rm E}\) は辺 \({\rm BC}\) を \(3:2\) に内分し、\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}\) より、
\(\overrightarrow{\rm AE}={\large \frac{2\overrightarrow{b}+3(\overrightarrow{b}+\overrightarrow{d})}{3+2}}\)
\(={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{5}}\)
また、点 \({\rm F}\) は辺 \({\rm BD}\) を \(3:5\) に内分するので、
\(\overrightarrow{\rm AF}={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{3+5}}\)
\(={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{8}}\)
よって、
\(\overrightarrow{\rm AF}={\large \frac{5}{8}}\cdot{\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{5}}\)
これより、
\(\overrightarrow{\rm AF}={\large \frac{5}{8}}\overrightarrow{\rm AE}\)
したがって、3点 \({\rm A~,~F~,~E}\) は一直線上にある [終]
→ 3点が同一直線上にある条件
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とすると
点 \({\rm E}\) は辺 \({\rm BC}\) を \(3:2\) に内分し、\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}\) より、
\(\overrightarrow{\rm AE}={\large \frac{2\overrightarrow{b}+3(\overrightarrow{b}+\overrightarrow{d})}{3+2}}\)
\(={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{5}}\)
また、点 \({\rm F}\) は辺 \({\rm BD}\) を \(3:5\) に内分するので、
\(\overrightarrow{\rm AF}={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{3+5}}\)
\(={\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{8}}\)
よって、
\(\overrightarrow{\rm AF}={\large \frac{5}{8}}\cdot{\large \frac{5\overrightarrow{b}+3\overrightarrow{d}}{5}}\)
これより、
\(\overrightarrow{\rm AF}={\large \frac{5}{8}}\overrightarrow{\rm AE}\)
したがって、3点 \({\rm A~,~F~,~E}\) は一直線上にある [終]
→ 3点が同一直線上にある条件
p.36 練習32
\(\overrightarrow{\rm OP}={\large \frac{1}{2}}\overrightarrow{a}+{\large \frac{1}{6}}\overrightarrow{b}\)
→ 2直線の交点とベクトル
\(\overrightarrow{\rm OP}={\large \frac{1}{2}}\overrightarrow{a}+{\large \frac{1}{6}}\overrightarrow{b}\)
→ 2直線の交点とベクトル
p.37 練習33
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とすると、\({\rm AB=AD}\) より \(|\overrightarrow{b}|=|\overrightarrow{d}|\)
次に、
\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}~,~\overrightarrow{\rm DB}=\overrightarrow{b}-\overrightarrow{d}\)
これより、
\(\overrightarrow{\rm AC}\cdot\overrightarrow{\rm DB}\)
\(=(\overrightarrow{b}+\overrightarrow{d})\cdot(\overrightarrow{b}-\overrightarrow{d})\)
\(=|\overrightarrow{b}|^2-|\overrightarrow{d}|^2\)
\(=0\)
よって、\(\overrightarrow{\rm AC}\neq\overrightarrow{0}~,~\overrightarrow{\rm DB}\neq\overrightarrow{0}\) であるので、
\(\overrightarrow{\rm AC}\perp\overrightarrow{\rm DB}\)
よって、\({\rm AC\perp DB}\)
したがって、
\({\rm AB=AD}\) ならば \({\rm AC\perp DB}\) [終]
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とすると、\({\rm AB=AD}\) より \(|\overrightarrow{b}|=|\overrightarrow{d}|\)
次に、
\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}~,~\overrightarrow{\rm DB}=\overrightarrow{b}-\overrightarrow{d}\)
これより、
\(\overrightarrow{\rm AC}\cdot\overrightarrow{\rm DB}\)
\(=(\overrightarrow{b}+\overrightarrow{d})\cdot(\overrightarrow{b}-\overrightarrow{d})\)
\(=|\overrightarrow{b}|^2-|\overrightarrow{d}|^2\)
\(=0\)
よって、\(\overrightarrow{\rm AC}\neq\overrightarrow{0}~,~\overrightarrow{\rm DB}\neq\overrightarrow{0}\) であるので、
\(\overrightarrow{\rm AC}\perp\overrightarrow{\rm DB}\)
よって、\({\rm AC\perp DB}\)
したがって、
\({\rm AB=AD}\) ならば \({\rm AC\perp DB}\) [終]
p.38 練習34

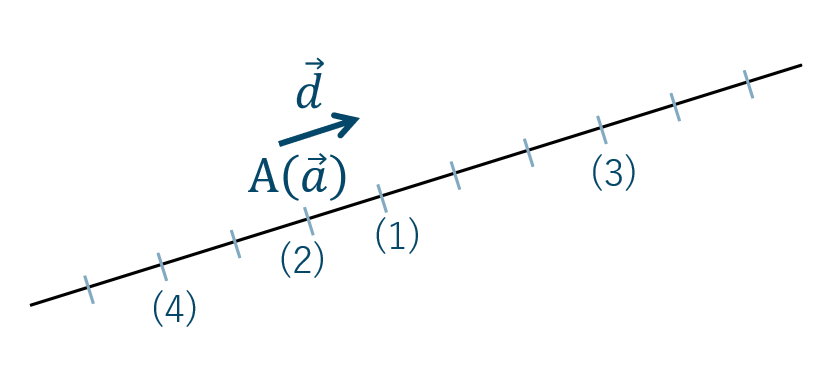
p.39 練習36

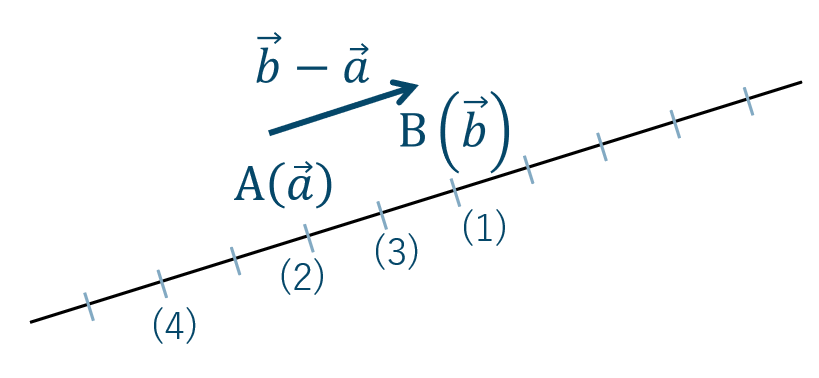
p.41 練習37
\(\overrightarrow{\rm OA’}={\large \frac{1}{2}}\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}={\large \frac{1}{2}}\overrightarrow{\rm OB}\) となる点を \({\rm A’~,~B’}\) とすると、線分 \({\rm A’B’}\)
→ ベクトルと点の存在範囲
\(\overrightarrow{\rm OA’}={\large \frac{1}{2}}\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}={\large \frac{1}{2}}\overrightarrow{\rm OB}\) となる点を \({\rm A’~,~B’}\) とすると、線分 \({\rm A’B’}\)
→ ベクトルと点の存在範囲
p.41 練習38
\({\small (1)}~x+2y-11=0\)
\({\small (2)}~3x-4y+11=0\)
\({\small (1)}~x+2y-11=0\)
\({\small (2)}~3x-4y+11=0\)
p.41 練習39
\({\small (1)}~\overrightarrow{n}=(3,2)\)
\({\small (2)}~\overrightarrow{n}=(2,1)\)
→ 法線ベクトル
\({\small (1)}~\overrightarrow{n}=(3,2)\)
\({\small (2)}~\overrightarrow{n}=(2,1)\)
→ 法線ベクトル
p.42 研究1
\({\small (1)}~\)中心 \(\overrightarrow{a}\)、半径 \(3\)
\({\small (2)}~\)中心 \({\large \frac{1}{2}}\overrightarrow{a}\)、半径 \(2\)
→ 円のベクトル方程式
\({\small (1)}~\)中心 \(\overrightarrow{a}\)、半径 \(3\)
\({\small (2)}~\)中心 \({\large \frac{1}{2}}\overrightarrow{a}\)、半径 \(2\)
→ 円のベクトル方程式
p.42 研究2
(ⅰ) \({\rm P}\) が \({\rm O}\) に一致するとき、
\(\overrightarrow{p}=\overrightarrow{0}\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
(ⅱ) \({\rm P}\) が \({\rm A}\) に一致するとき、
\(\overrightarrow{p}=\overrightarrow{a}\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
(ⅲ) \({\rm P}\) が \({\rm O~,~A}\) に一致しないとき、
\({\rm OP\perp AP}~\Leftrightarrow~\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AP}=0\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
したがって、このベクトル方程式は、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\) [終]
(ⅰ) \({\rm P}\) が \({\rm O}\) に一致するとき、
\(\overrightarrow{p}=\overrightarrow{0}\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
(ⅱ) \({\rm P}\) が \({\rm A}\) に一致するとき、
\(\overrightarrow{p}=\overrightarrow{a}\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
(ⅲ) \({\rm P}\) が \({\rm O~,~A}\) に一致しないとき、
\({\rm OP\perp AP}~\Leftrightarrow~\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AP}=0\)
よって、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\)
したがって、このベクトル方程式は、
\(\overrightarrow{p}\cdot(\overrightarrow{p}-\overrightarrow{a})=0\) [終]
補充問題
p.44 4
[証明]
\(\overrightarrow{\rm HA}=\overrightarrow{a}~,~\overrightarrow{\rm HB}=\overrightarrow{b}~,~\overrightarrow{\rm HC}=\overrightarrow{c}\) とすると、
\({\rm HB}\perp {\rm CA}\) より、\(\overrightarrow{\rm HB}\cdot\overrightarrow{\rm CA}=0\)
よって、
\(\overrightarrow{b}\cdot(\overrightarrow{a}-\overrightarrow{c})=0\)
これより、
\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}\) …①
また、同様に \({\rm HC}\perp {\rm AB}\) より、\(\overrightarrow{\rm HC}\cdot\overrightarrow{\rm AB}=0\)
よって、
\(\overrightarrow{c}\cdot(\overrightarrow{b}-\overrightarrow{a})=0\)
これより、
\(\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{a}\cdot\overrightarrow{c}\) …②
ここで、
\(~~~~~~\overrightarrow{\rm HA}\cdot\overrightarrow{\rm BC}\)
\(~=\overrightarrow{a}\cdot(\overrightarrow{c}-\overrightarrow{b})\)
\(~=\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}\)
①、②を代入すると、
\(~=\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{c}\)
\(~=0\)
したがって、\(\overrightarrow{\rm HA}\neq\overrightarrow{0}~,~\overrightarrow{\rm BC}\neq\overrightarrow{0}\) であるから \(\overrightarrow{\rm HA}\perp\overrightarrow{\rm BC}\) より、
\({\rm HA}\perp{\rm BC}\) [終]
[証明]
\(\overrightarrow{\rm HA}=\overrightarrow{a}~,~\overrightarrow{\rm HB}=\overrightarrow{b}~,~\overrightarrow{\rm HC}=\overrightarrow{c}\) とすると、
\({\rm HB}\perp {\rm CA}\) より、\(\overrightarrow{\rm HB}\cdot\overrightarrow{\rm CA}=0\)
よって、
\(\overrightarrow{b}\cdot(\overrightarrow{a}-\overrightarrow{c})=0\)
これより、
\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}\) …①
また、同様に \({\rm HC}\perp {\rm AB}\) より、\(\overrightarrow{\rm HC}\cdot\overrightarrow{\rm AB}=0\)
よって、
\(\overrightarrow{c}\cdot(\overrightarrow{b}-\overrightarrow{a})=0\)
これより、
\(\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{a}\cdot\overrightarrow{c}\) …②
ここで、
\(~~~~~~\overrightarrow{\rm HA}\cdot\overrightarrow{\rm BC}\)
\(~=\overrightarrow{a}\cdot(\overrightarrow{c}-\overrightarrow{b})\)
\(~=\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}\)
①、②を代入すると、
\(~=\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{c}\)
\(~=0\)
したがって、\(\overrightarrow{\rm HA}\neq\overrightarrow{0}~,~\overrightarrow{\rm BC}\neq\overrightarrow{0}\) であるから \(\overrightarrow{\rm HA}\perp\overrightarrow{\rm BC}\) より、
\({\rm HA}\perp{\rm BC}\) [終]
p.44 5
[証明] \(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) とすると
\(\overrightarrow{\rm OD}={\large \frac{2}{3}}\overrightarrow{a}~,~\overrightarrow{\rm OE}={\large \frac{2}{3}}\overrightarrow{c}\)
よって、
\(\overrightarrow{\rm DE}=\overrightarrow{\rm OE}-\overrightarrow{\rm OD}={\large \frac{2}{3}}\overrightarrow{c}-{\large \frac{2}{3}}\overrightarrow{a}\)
次に、
\(\overrightarrow{\rm OF}={\large \frac{1}{3}}\overrightarrow{\rm OB}={\large \frac{1}{3}}(\overrightarrow{a}+\overrightarrow{c})\)
これより、
\(\overrightarrow{\rm DF}=\overrightarrow{\rm OF}-\overrightarrow{\rm OD}={\large \frac{1}{3}}\overrightarrow{c}-{\large \frac{1}{3}}\overrightarrow{a}\)
よって、
\(\overrightarrow{\rm DE}=2\left({\large \frac{1}{3}}\overrightarrow{c}-{\large \frac{1}{3}}\overrightarrow{a}\right)\)
これより、
\(\overrightarrow{\rm DE}=2\overrightarrow{\rm DF}\)
したがって、3点 \({\rm D~,~F~,~E}\) は一直線上にある [終]
[証明] \(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) とすると
\(\overrightarrow{\rm OD}={\large \frac{2}{3}}\overrightarrow{a}~,~\overrightarrow{\rm OE}={\large \frac{2}{3}}\overrightarrow{c}\)
よって、
\(\overrightarrow{\rm DE}=\overrightarrow{\rm OE}-\overrightarrow{\rm OD}={\large \frac{2}{3}}\overrightarrow{c}-{\large \frac{2}{3}}\overrightarrow{a}\)
次に、
\(\overrightarrow{\rm OF}={\large \frac{1}{3}}\overrightarrow{\rm OB}={\large \frac{1}{3}}(\overrightarrow{a}+\overrightarrow{c})\)
これより、
\(\overrightarrow{\rm DF}=\overrightarrow{\rm OF}-\overrightarrow{\rm OD}={\large \frac{1}{3}}\overrightarrow{c}-{\large \frac{1}{3}}\overrightarrow{a}\)
よって、
\(\overrightarrow{\rm DE}=2\left({\large \frac{1}{3}}\overrightarrow{c}-{\large \frac{1}{3}}\overrightarrow{a}\right)\)
これより、
\(\overrightarrow{\rm DE}=2\overrightarrow{\rm DF}\)
したがって、3点 \({\rm D~,~F~,~E}\) は一直線上にある [終]
章末問題 平面上のベクトル
章末問題A
p.45 1
\({\small (1)}~{\large \frac{1}{2}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{d}\)
\({\small (2)}~-{\large \frac{1}{2}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{d}\)
\({\small (3)}~-{\large \frac{1}{2}}\overrightarrow{b}-{\large \frac{1}{2}}\overrightarrow{d}\)
\({\small (1)}~{\large \frac{1}{2}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{d}\)
\({\small (2)}~-{\large \frac{1}{2}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{d}\)
\({\small (3)}~-{\large \frac{1}{2}}\overrightarrow{b}-{\large \frac{1}{2}}\overrightarrow{d}\)
p.45 2
\({\small (1)}~t=-3~,~1\)
\({\small (2)}~\)[証明]
\(|\overrightarrow{c}|^2\)
\(=(3+t)^2+(1+2t)^2\)
\(=5t^2+10t+10\)
\(=5(t+1)^2+5\)
ここで、\(|\overrightarrow{c}|≧0\) であるので \(|\overrightarrow{c}|^2\) が最小のとき \(|\overrightarrow{c}|\) も最小となる
よって、\(t=-1\) のとき \(|\overrightarrow{c}|\) が最小となる
これより、
\(\overrightarrow{c}\)
\(=(3-1,1+2\times(-1))\)
\(=(2,-1)\)
よって、
\(\overrightarrow{b}\cdot\overrightarrow{c}\)
\(=1\times2+2\times(-1)\)
\(=0\)
したがって、\(\overrightarrow{b}\neq\overrightarrow{0}~,~\overrightarrow{c}\neq\overrightarrow{0}\) であるので、
\(\overrightarrow{b}\perp\overrightarrow{c}\) [終]
\({\small (1)}~t=-3~,~1\)
\({\small (2)}~\)[証明]
\(|\overrightarrow{c}|^2\)
\(=(3+t)^2+(1+2t)^2\)
\(=5t^2+10t+10\)
\(=5(t+1)^2+5\)
ここで、\(|\overrightarrow{c}|≧0\) であるので \(|\overrightarrow{c}|^2\) が最小のとき \(|\overrightarrow{c}|\) も最小となる
よって、\(t=-1\) のとき \(|\overrightarrow{c}|\) が最小となる
これより、
\(\overrightarrow{c}\)
\(=(3-1,1+2\times(-1))\)
\(=(2,-1)\)
よって、
\(\overrightarrow{b}\cdot\overrightarrow{c}\)
\(=1\times2+2\times(-1)\)
\(=0\)
したがって、\(\overrightarrow{b}\neq\overrightarrow{0}~,~\overrightarrow{c}\neq\overrightarrow{0}\) であるので、
\(\overrightarrow{b}\perp\overrightarrow{c}\) [終]
p.45 3
\({\small (1)}~1\) \({\small (2)}~60^\circ\)
\({\small (1)}~1\) \({\small (2)}~60^\circ\)
p.45 4

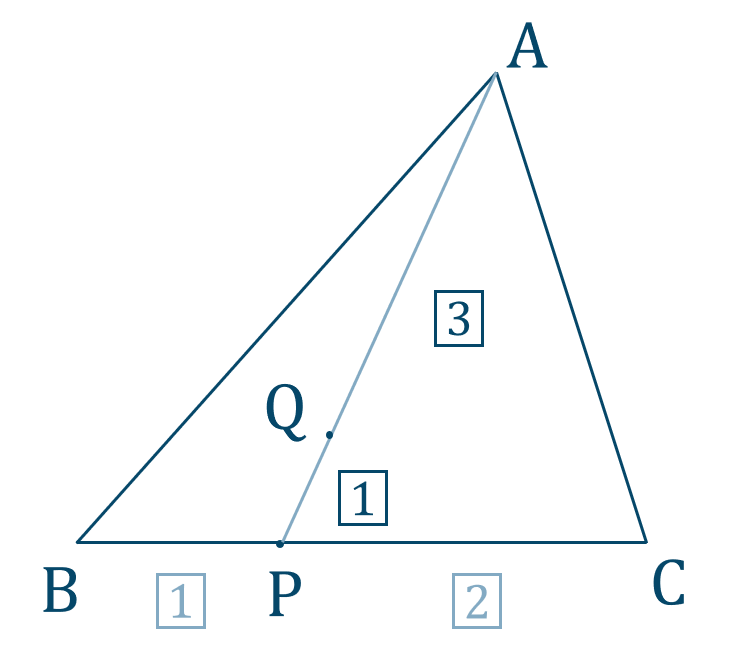
p.45 5
\({\small (1)}~\overrightarrow{\rm AP}={\large \frac{1}{6}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{c}\)
\({\small (2)}~\)[証明] \(\overrightarrow{\rm AF}={\large \frac{3}{5}}\overrightarrow{c}\) より、
\(\overrightarrow{\rm BF}\)
\(=\overrightarrow{\rm AF}-\overrightarrow{\rm AB}\)
\(={\large \frac{3}{5}}\overrightarrow{c}-\overrightarrow{b}\)
\(={\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{5}}\)
次に、
\(\overrightarrow{\rm BP}\)
\(=\overrightarrow{\rm AP}-\overrightarrow{\rm AB}\)
\(={\large \frac{1}{6}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{c}-\overrightarrow{b}\)
\(={\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{6}}\)
\(={\large \frac{5}{6}}\cdot{\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{5}}\)
よって、
\(\overrightarrow{\rm BP}={\large \frac{5}{6}}\overrightarrow{\rm BF}\)
したがって、3点 \({\rm B~,~P~,~F}\) は同一直線上にある [終]
\({\small (1)}~\overrightarrow{\rm AP}={\large \frac{1}{6}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{c}\)
\({\small (2)}~\)[証明] \(\overrightarrow{\rm AF}={\large \frac{3}{5}}\overrightarrow{c}\) より、
\(\overrightarrow{\rm BF}\)
\(=\overrightarrow{\rm AF}-\overrightarrow{\rm AB}\)
\(={\large \frac{3}{5}}\overrightarrow{c}-\overrightarrow{b}\)
\(={\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{5}}\)
次に、
\(\overrightarrow{\rm BP}\)
\(=\overrightarrow{\rm AP}-\overrightarrow{\rm AB}\)
\(={\large \frac{1}{6}}\overrightarrow{b}+{\large \frac{1}{2}}\overrightarrow{c}-\overrightarrow{b}\)
\(={\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{6}}\)
\(={\large \frac{5}{6}}\cdot{\large \frac{-5\overrightarrow{b}+3\overrightarrow{c}}{5}}\)
よって、
\(\overrightarrow{\rm BP}={\large \frac{5}{6}}\overrightarrow{\rm BF}\)
したがって、3点 \({\rm B~,~P~,~F}\) は同一直線上にある [終]
章末問題B
p.46 6
\({\small (1)}~\)
最大値 \(2\)、最小値 \(-2\)
\({\small (2)}~\)
最大値 \(3\)、最小値 \(1\)
\({\small (1)}~\)
最大値 \(2\)、最小値 \(-2\)
\({\small (2)}~\)
最大値 \(3\)、最小値 \(1\)
p.46 7
\({\small (1)}~\)辺 \({\rm BC}\) を \(5:4\) に内分する点を \({\rm Q}\) として、\({\rm AQ}\) を \(3:1\) に内分する点
\({\small (2)}~3:4:5\)
\({\small (1)}~\)辺 \({\rm BC}\) を \(5:4\) に内分する点を \({\rm Q}\) として、\({\rm AQ}\) を \(3:1\) に内分する点
\({\small (2)}~3:4:5\)
p.46 8
\({\small (1)}~\)[証明] \({\rm G}\) は \(\triangle {\rm ABC}\) の重心であるので、
\(\overrightarrow{\rm OG}={\large \frac{\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}}{3}}\)
よって、
\(\overrightarrow{\rm OG}={\large \frac{1}{3}}\overrightarrow{\rm OH}\)
したがって、3点 \({\rm O~,~G~,~H}\) は同一直線上にある [終]
\({\small (2)}~\)[証明]
\(\overrightarrow{\rm BH}\)
\(=\overrightarrow{\rm OH}-\overrightarrow{\rm OB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC})-\overrightarrow{\rm OB}\)
\(=\overrightarrow{\rm OA}+\overrightarrow{\rm OC}\)
よって、
\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OC})\cdot(\overrightarrow{\rm OA}-\overrightarrow{\rm OC})\)
\(=|\overrightarrow{\rm OA}|^2-|\overrightarrow{\rm OC}|^2\)
ここで、\({\rm OA~,~OC}\) は外接円の半径より、
\(=0\)
よって、
\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm CA}=0\) …①
また、
\(\overrightarrow{\rm CH}\)
\(=\overrightarrow{\rm OH}-\overrightarrow{\rm OB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC})-\overrightarrow{\rm OC}\)
\(=\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\)
よって、
\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB})\cdot(\overrightarrow{\rm OA}-\overrightarrow{\rm OB})\)
\(=|\overrightarrow{\rm OA}|^2-|\overrightarrow{\rm OB}|^2\)
ここで、\({\rm OA~,~OB}\) は外接円の半径より、
\(=0\)
よって、
\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}=0\) …②
①と②と\(\overrightarrow{\rm BH}~,~\overrightarrow{\rm CA}~,~\overrightarrow{\rm CH}~,~\overrightarrow{\rm AB}\) が \(\overrightarrow{0}\) でないことより、
\(\overrightarrow{\rm BH}\perp\overrightarrow{\rm CA}\) かつ \(\overrightarrow{\rm CH}\perp\overrightarrow{\rm AB}\)
したがって、
\({\rm BH\perp CA}\) かつ \({\rm CH\perp AB}\)
[終]
\({\small (1)}~\)[証明] \({\rm G}\) は \(\triangle {\rm ABC}\) の重心であるので、
\(\overrightarrow{\rm OG}={\large \frac{\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}}{3}}\)
よって、
\(\overrightarrow{\rm OG}={\large \frac{1}{3}}\overrightarrow{\rm OH}\)
したがって、3点 \({\rm O~,~G~,~H}\) は同一直線上にある [終]
\({\small (2)}~\)[証明]
\(\overrightarrow{\rm BH}\)
\(=\overrightarrow{\rm OH}-\overrightarrow{\rm OB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC})-\overrightarrow{\rm OB}\)
\(=\overrightarrow{\rm OA}+\overrightarrow{\rm OC}\)
よって、
\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm CA}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OC})\cdot(\overrightarrow{\rm OA}-\overrightarrow{\rm OC})\)
\(=|\overrightarrow{\rm OA}|^2-|\overrightarrow{\rm OC}|^2\)
ここで、\({\rm OA~,~OC}\) は外接円の半径より、
\(=0\)
よって、
\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm CA}=0\) …①
また、
\(\overrightarrow{\rm CH}\)
\(=\overrightarrow{\rm OH}-\overrightarrow{\rm OB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC})-\overrightarrow{\rm OC}\)
\(=\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\)
よって、
\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}\)
\(=(\overrightarrow{\rm OA}+\overrightarrow{\rm OB})\cdot(\overrightarrow{\rm OA}-\overrightarrow{\rm OB})\)
\(=|\overrightarrow{\rm OA}|^2-|\overrightarrow{\rm OB}|^2\)
ここで、\({\rm OA~,~OB}\) は外接円の半径より、
\(=0\)
よって、
\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}=0\) …②
①と②と\(\overrightarrow{\rm BH}~,~\overrightarrow{\rm CA}~,~\overrightarrow{\rm CH}~,~\overrightarrow{\rm AB}\) が \(\overrightarrow{0}\) でないことより、
\(\overrightarrow{\rm BH}\perp\overrightarrow{\rm CA}\) かつ \(\overrightarrow{\rm CH}\perp\overrightarrow{\rm AB}\)
したがって、
\({\rm BH\perp CA}\) かつ \({\rm CH\perp AB}\)
[終]
p.46 9
\({\small (1)}~{\large \frac{6}{5}}\) \({\small (2)}~2:3\)
\({\small (1)}~{\large \frac{6}{5}}\) \({\small (2)}~2:3\)
p.46 10
\({\small (1)}~-{\large \frac{2}{5}}\)
\({\small (2)}~\left(-{\large \frac{1}{5}},{\large \frac{2}{5}}\right)~,~2\)
\({\small (1)}~-{\large \frac{2}{5}}\)
\({\small (2)}~\left(-{\large \frac{1}{5}},{\large \frac{2}{5}}\right)~,~2\)
次のページ「第2章 空間のベクトル」