文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第4章 三角関数
第6章 微分法と積分法
第5章 指数関数と対数関数
p.156
練習1
\({\small (1)}~1\) \({\small (2)}~{\large \frac{1}{9}}\) \({\small (3)}~{\large \frac{1}{1000}}\)
\({\small (5)}~-{\large \frac{1}{125}}\) \({\small (6)}~25\)
練習1
\({\small (1)}~1\) \({\small (2)}~{\large \frac{1}{9}}\) \({\small (3)}~{\large \frac{1}{1000}}\)
\({\small (5)}~-{\large \frac{1}{125}}\) \({\small (6)}~25\)
p.157
問1
\({\small (1)}~a\) \({\small (2)}~a^6\) \({\small (3)}~{\large \frac{b^2}{a^2}}\) \({\small (4)}~{\large \frac{1}{a^3}}\)
問1
\({\small (1)}~a\) \({\small (2)}~a^6\) \({\small (3)}~{\large \frac{b^2}{a^2}}\) \({\small (4)}~{\large \frac{1}{a^3}}\)
p.157
練習2
\({\small (1)}~{\large \frac{1}{a^2}}\) \({\small (2)}~a^3\) \({\small (3)}~{\large \frac{a^3}{b^3}}\) \({\small (4)}~{\large \frac{1}{a^2}}\)
→ 指数法則の基本
練習2
\({\small (1)}~{\large \frac{1}{a^2}}\) \({\small (2)}~a^3\) \({\small (3)}~{\large \frac{a^3}{b^3}}\) \({\small (4)}~{\large \frac{1}{a^2}}\)
→ 指数法則の基本
p.158
練習3
\({\small (1)}~7\) \({\small (2)}~2\) \({\small (3)}~0.1\)
練習3
\({\small (1)}~7\) \({\small (2)}~2\) \({\small (3)}~0.1\)
p.159
問2
[証明]
性質2$$~\left(\frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}\right)^n=\frac{(\sqrt[\large n]{a})^n}{(\sqrt[\large n]{a})^n}=\frac{a}{b}$$\({\large \frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}}>0\) より、両辺に \(n\) 乗根をとると、$$~~~\frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}=\sqrt[\large n]{\frac{a}{b}}$$
性質3$$~\{(\sqrt[\large n]{a})^m\}^n=(\sqrt[\large n]{a})^{mn}$$$$~~~~~~=\{(\sqrt[\large n]{a})^n\}^m=a^m$$\((\sqrt[\large n]{a})^m>0\) より、両辺に \(n\) 乗根をとると、$$~~~(\sqrt[\large n]{a})^m=\sqrt[\large n]{a^m}$$
性質4$$~\left(\sqrt[\large m]{\sqrt[\large n]{a}}\right)^{mn}=\left\{\left(\sqrt[\large m]{\sqrt[\large n]{a}}\right)^{m}\right\}^n$$$$~~~~~~=(\sqrt[\large n]{a})^n=a$$\(\sqrt[\large m]{\sqrt[\large n]{a}}>0\) より、両辺に \(mn\) 乗根をとると、$$~~~\sqrt[\large m]{\sqrt[\large n]{a}}=\sqrt[\large mn]{a}$$
性質5$$~(\sqrt[\large n]{a^m})^{np}=\left\{ \left(\sqrt[\large n]{a^m} \right)^{n} \right\}^p$$$$~~~~~~=(a^m)^p=a^{mp}$$\(\sqrt[\large n]{a^m}>0\) より、両辺に \(n\) 乗根をとると、$$~~~\sqrt[\large n]{a^m}=\sqrt[\large np]{a^{mp}}$$[終]
問2
[証明]
性質2$$~\left(\frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}\right)^n=\frac{(\sqrt[\large n]{a})^n}{(\sqrt[\large n]{a})^n}=\frac{a}{b}$$\({\large \frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}}>0\) より、両辺に \(n\) 乗根をとると、$$~~~\frac{\sqrt[\large n]{a}}{\sqrt[\large n]{b}}=\sqrt[\large n]{\frac{a}{b}}$$
性質3$$~\{(\sqrt[\large n]{a})^m\}^n=(\sqrt[\large n]{a})^{mn}$$$$~~~~~~=\{(\sqrt[\large n]{a})^n\}^m=a^m$$\((\sqrt[\large n]{a})^m>0\) より、両辺に \(n\) 乗根をとると、$$~~~(\sqrt[\large n]{a})^m=\sqrt[\large n]{a^m}$$
性質4$$~\left(\sqrt[\large m]{\sqrt[\large n]{a}}\right)^{mn}=\left\{\left(\sqrt[\large m]{\sqrt[\large n]{a}}\right)^{m}\right\}^n$$$$~~~~~~=(\sqrt[\large n]{a})^n=a$$\(\sqrt[\large m]{\sqrt[\large n]{a}}>0\) より、両辺に \(mn\) 乗根をとると、$$~~~\sqrt[\large m]{\sqrt[\large n]{a}}=\sqrt[\large mn]{a}$$
性質5$$~(\sqrt[\large n]{a^m})^{np}=\left\{ \left(\sqrt[\large n]{a^m} \right)^{n} \right\}^p$$$$~~~~~~=(a^m)^p=a^{mp}$$\(\sqrt[\large n]{a^m}>0\) より、両辺に \(n\) 乗根をとると、$$~~~\sqrt[\large n]{a^m}=\sqrt[\large np]{a^{mp}}$$[終]
p.159
練習4
\({\small (1)}~3\) \({\small (2)}~2\) \({\small (3)}~5\)
\({\small (4)}~3\) \({\small (5)}~\sqrt{2}\)
→ 累乗根
練習4
\({\small (1)}~3\) \({\small (2)}~2\) \({\small (3)}~5\)
\({\small (4)}~3\) \({\small (5)}~\sqrt{2}\)
→ 累乗根
p.161
練習6
\({\small (1)}~2\) \({\small (2)}~{\large \frac{3}{4}}\) \({\small (3)}~3\)
\({\small (4)}~a\sqrt[\large 3]{a^2}\) \({\small (5)}~a\)
→ 指数法則を用いた計算
練習6
\({\small (1)}~2\) \({\small (2)}~{\large \frac{3}{4}}\) \({\small (3)}~3\)
\({\small (4)}~a\sqrt[\large 3]{a^2}\) \({\small (5)}~a\)
→ 指数法則を用いた計算
p.163
問3
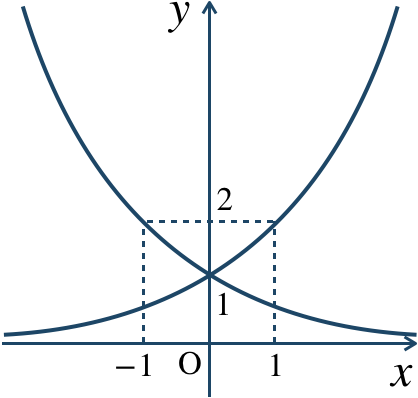
[証明] \(f(x)=2^x\) とすると、$$~~~f(-x)=2^{-x}=\left(\frac{1}{2}\right)^x$$これより、\(y\) 軸に関して対称である [終]

問3
[証明] \(f(x)=2^x\) とすると、$$~~~f(-x)=2^{-x}=\left(\frac{1}{2}\right)^x$$これより、\(y\) 軸に関して対称である [終]
p.164
練習8
\({\small (1)}~\sqrt[\large 3]{3}<\sqrt[\large 7]{27}<\sqrt[\large 4]{9}\)
\({\small (2)}~\sqrt[\large 4]{{\large \frac{1}{8}}}<\sqrt[\large 3]{{\large \frac{1}{4}}}<\sqrt{{\large \frac{1}{2}}}\)
→ 指数の大小比較
練習8
\({\small (1)}~\sqrt[\large 3]{3}<\sqrt[\large 7]{27}<\sqrt[\large 4]{9}\)
\({\small (2)}~\sqrt[\large 4]{{\large \frac{1}{8}}}<\sqrt[\large 3]{{\large \frac{1}{4}}}<\sqrt{{\large \frac{1}{2}}}\)
→ 指数の大小比較
p.165
練習9
\({\small (1)}~x={\large \frac{2}{3}}\) \({\small (2)}~x=3\)
\({\small (3)}~x=1\) \({\small (4)}~x<5\)
\({\small (5)}~x≧5\) \({\small (6)}~x>{\large \frac{1}{2}}\)
→ 指数方程式
→ 指数不等式
練習9
\({\small (1)}~x={\large \frac{2}{3}}\) \({\small (2)}~x=3\)
\({\small (3)}~x=1\) \({\small (4)}~x<5\)
\({\small (5)}~x≧5\) \({\small (6)}~x>{\large \frac{1}{2}}\)
→ 指数方程式
→ 指数不等式
p.165
練習10
\({\small (1)}~x=2\) \({\small (2)}~x=-1~,~1\)
\({\small (3)}~x>3\) \({\small (4)}~x>1\)
→ 指数関数を含む2次方程式
→ 指数関数を含む2次不等式
練習10
\({\small (1)}~x=2\) \({\small (2)}~x=-1~,~1\)
\({\small (3)}~x>3\) \({\small (4)}~x>1\)
→ 指数関数を含む2次方程式
→ 指数関数を含む2次不等式
p.166
練習11
\({\small (1)}~5=\log_{3}243\)
\({\small (2)}~{\large \frac{1}{3}}=\log_{8}2\)
\({\small (3)}~-1=\log_{10}0.1\)
練習11
\({\small (1)}~5=\log_{3}243\)
\({\small (2)}~{\large \frac{1}{3}}=\log_{8}2\)
\({\small (3)}~-1=\log_{10}0.1\)
p.166
練習12
\({\small (1)}~2^3=8\) \({\small (2)}~10^{-5}={\large \frac{1}{100000}}\)
\({\small (3)}~3^{{\large \frac{1}{2}}}=\sqrt{3}\)
→ 指数と対数
練習12
\({\small (1)}~2^3=8\) \({\small (2)}~10^{-5}={\large \frac{1}{100000}}\)
\({\small (3)}~3^{{\large \frac{1}{2}}}=\sqrt{3}\)
→ 指数と対数
p.167
練習13
\({\small (1)}~5\) \({\small (2)}~{\large \frac{3}{2}}\) \({\small (3)}~-3\)
\({\small (4)}~{\large \frac{1}{2}}\) \({\small (5)}~-2\) \({\small (6)}~-3\)
→ 対数の値
練習13
\({\small (1)}~5\) \({\small (2)}~{\large \frac{3}{2}}\) \({\small (3)}~-3\)
\({\small (4)}~{\large \frac{1}{2}}\) \({\small (5)}~-2\) \({\small (6)}~-3\)
→ 対数の値
p.168
練習14
\({\small (1)}~2\) \({\small (2)}~-1\) \({\small (3)}~{\large \frac{1}{3}}\) \({\small (4)}~{\large \frac{3}{2}}\)
→ 対数の計算
練習14
\({\small (1)}~2\) \({\small (2)}~-1\) \({\small (3)}~{\large \frac{1}{3}}\) \({\small (4)}~{\large \frac{3}{2}}\)
→ 対数の計算
p.169
練習15
\({\small (1)}~{\large \frac{3}{2}}\) \({\small (2)}~{\large \frac{1}{3}}\) \({\small (3)}~3\)
→ 底の変換公式
練習15
\({\small (1)}~{\large \frac{3}{2}}\) \({\small (2)}~{\large \frac{1}{3}}\) \({\small (3)}~3\)
→ 底の変換公式
p.169
問4
[証明] 底の変換公式より、$$~~~~~~\log_{a}b \cdot\log_{b}c\cdot\log_{c}a$$$$~=\log_{a}b \cdot\frac{\log_{a}c}{\log_{a}b}\cdot\frac{\log_{a}a}{\log_{a}c}$$$$~=\log_{a}a=1$$[終]
問4
[証明] 底の変換公式より、$$~~~~~~\log_{a}b \cdot\log_{b}c\cdot\log_{c}a$$$$~=\log_{a}b \cdot\frac{\log_{a}c}{\log_{a}b}\cdot\frac{\log_{a}a}{\log_{a}c}$$$$~=\log_{a}a=1$$[終]
p.169
練習16
[証明] 底の変換公式より、$$~~~~~~\log_{a}b \cdot\log_{b}c\cdot\log_{c}d$$$$~=\log_{a}b \cdot\frac{\log_{a}c}{\log_{a}b}\cdot\frac{\log_{a}d}{\log_{a}c}$$$$~=\log_{a}d$$[終]
練習16
[証明] 底の変換公式より、$$~~~~~~\log_{a}b \cdot\log_{b}c\cdot\log_{c}d$$$$~=\log_{a}b \cdot\frac{\log_{a}c}{\log_{a}b}\cdot\frac{\log_{a}d}{\log_{a}c}$$$$~=\log_{a}d$$[終]
p.171
問5
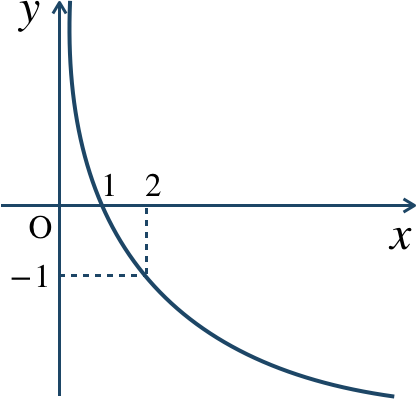
[証明] \(f(x)=\log_{2}x\) とすると、底の変換公式より、$$~\log_{{\large \frac{1}{2}}}x=\frac{\log_{2}x}{\log_{2}{\large \frac{1}{2}}}$$$$~~~~~~=-\log_{2}x=-f(x)$$したがって、\(x\) 軸に関して対称である [終]

問5
[証明] \(f(x)=\log_{2}x\) とすると、底の変換公式より、$$~\log_{{\large \frac{1}{2}}}x=\frac{\log_{2}x}{\log_{2}{\large \frac{1}{2}}}$$$$~~~~~~=-\log_{2}x=-f(x)$$したがって、\(x\) 軸に関して対称である [終]
p.172
練習19
\({\small (1)}~x=3\sqrt{3}\) \({\small (2)}~x=8\)
\({\small (3)}~0<x<9\) \({\small (4)}~0<x≦0.25\)
練習19
\({\small (1)}~x=3\sqrt{3}\) \({\small (2)}~x=8\)
\({\small (3)}~0<x<9\) \({\small (4)}~0<x≦0.25\)
p.173
練習20
\({\small (1)}~x=18\) \({\small (2)}~-2<x<7\)
\({\small (3)}~x≧{\large \frac{10}{9}}\)
→ 対数方程式
→ 対数不等式
練習20
\({\small (1)}~x=18\) \({\small (2)}~-2<x<7\)
\({\small (3)}~x≧{\large \frac{10}{9}}\)
→ 対数方程式
→ 対数不等式
p.173
練習21
\({\small (1)}~x=9\) \({\small (2)}~x=3\)
練習21
\({\small (1)}~x=9\) \({\small (2)}~x=3\)
p.175
問6
\({\small (1)}~1.8156\) \({\small (2)}~3.4742\)
\({\small (3)}~-0.0410\)
問6
\({\small (1)}~1.8156\) \({\small (2)}~3.4742\)
\({\small (3)}~-0.0410\)
p.175
練習24
\({\small (1)}~1.2552\) \({\small (2)}~-0.2219\)
\({\small (3)}~1.3980\) \({\small (4)}~3.0960\)
練習24
\({\small (1)}~1.2552\) \({\small (2)}~-0.2219\)
\({\small (3)}~1.3980\) \({\small (4)}~3.0960\)
p.176
練習25
\(31\) 桁
練習25
\(31\) 桁
p.177
問7
\(n=10\)
問7
\(n=10\)
p.177
練習27
\(n=25\)
練習27
\(n=25\)
p.177
練習28
\(7\) 枚
練習28
\(7\) 枚
p.178
研究1
\({\small (1)}~\)[証明]
\(\log_{2}5>0\) であり、これが有理数であると仮定すると、自然数 \(m~,~n\) を用いて$$~~~\log_{2}5=\frac{m}{n}$$これより、$$~~~2^{\large \frac{m}{n}}=5~\Leftrightarrow~2^m=5^n$$となるが、左辺が2の倍数であるが右辺は2の倍数でないので矛盾する
したがって、\(\log_{2}5\) は無理数である [終]
研究1
\({\small (1)}~\)[証明]
\(\log_{2}5>0\) であり、これが有理数であると仮定すると、自然数 \(m~,~n\) を用いて$$~~~\log_{2}5=\frac{m}{n}$$これより、$$~~~2^{\large \frac{m}{n}}=5~\Leftrightarrow~2^m=5^n$$となるが、左辺が2の倍数であるが右辺は2の倍数でないので矛盾する
したがって、\(\log_{2}5\) は無理数である [終]
\({\small (2)}~\)[証明]$$~~~~~~\log_{2}10$$$$~=\log_{2}(2\times5)=1+\log_{2}5$$(1)より、\(\log_{2}5\) は無理数であるので、\(1+\log_{2}5\) も無理数である
したがって、\(\log_{2}10\) は無理数である [終]
\({\small (3)}~\)[証明] 底の変換公式より、$$~~~\log_{10}2=\frac{1}{\log_{2}10}$$(2)より、\(\log_{2}10\) は無理数であるので、\({\large \frac{1}{\log_{2}10}}\) も無理数である
したがって、\(\log_{10}2\) は無理数である [終]
問題
p.179
1
\({\small (1)}~1\) \({\small (2)}~5\)
1
\({\small (1)}~1\) \({\small (2)}~5\)
p.179
2
\({\small (1)}~x={\large \frac{2}{3}}\) \({\small (2)}~x=1\)
\({\small (3)}~x≦-4\) \({\small (4)}~x>-1\)
\({\small (5)}~x=1\) \({\small (6)}~x<-1~,~2<x\)
2
\({\small (1)}~x={\large \frac{2}{3}}\) \({\small (2)}~x=1\)
\({\small (3)}~x≦-4\) \({\small (4)}~x>-1\)
\({\small (5)}~x=1\) \({\small (6)}~x<-1~,~2<x\)
p.179
3
\({\small (1)}~0\) \({\small (2)}~{\large \frac{10}{3}}\) \({\small (3)}~5\)
3
\({\small (1)}~0\) \({\small (2)}~{\large \frac{10}{3}}\) \({\small (3)}~5\)
p.179
4
\({\small (1)}~2p+3q+r\)
\({\small (2)}~3p-2q-r\)
\({\small (3)}~p-q+{\large \frac{3}{2}}r-2\)
4
\({\small (1)}~2p+3q+r\)
\({\small (2)}~3p-2q-r\)
\({\small (3)}~p-q+{\large \frac{3}{2}}r-2\)
p.179
5

\(x\) 軸に関して対称
5
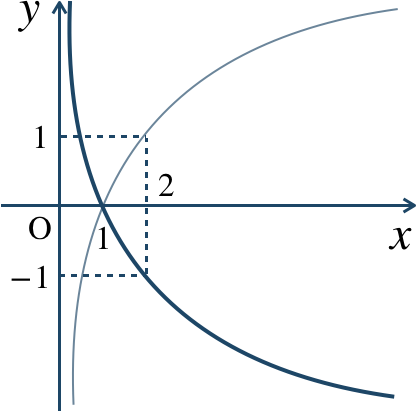
\(x\) 軸に関して対称
p.179
6
\({\small (1)}~x=6~,~-10\) \({\small (2)}~x=5\)
\({\small (3)}~0<x<2~,~4<x<6\)
\({\small (4)}~2<x≦3\)
6
\({\small (1)}~x=6~,~-10\) \({\small (2)}~x=5\)
\({\small (3)}~0<x<2~,~4<x<6\)
\({\small (4)}~2<x≦3\)
p.179
7
\(24\) 桁
7
\(24\) 桁
演習問題 指数関数と対数関数
演習問題A
p.180
1
\({\small (1)}~7\) \({\small (2)}~47\)
1
\({\small (1)}~7\) \({\small (2)}~47\)
p.180
2
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

2
\({\small (1)}~\)
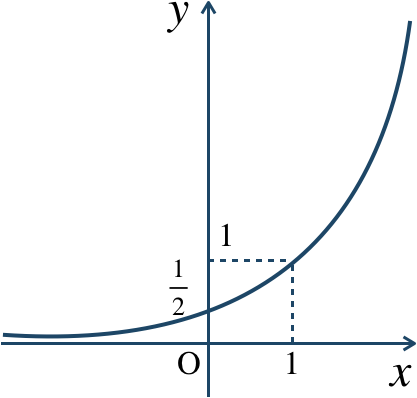
\({\small (2)}~\)
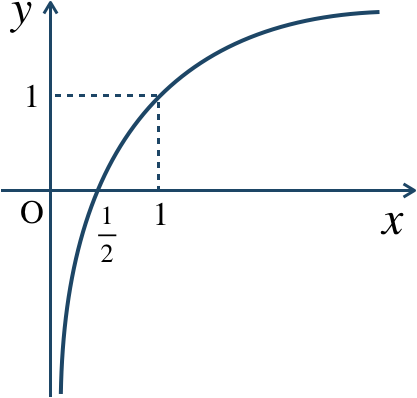
\({\small (3)}~\)
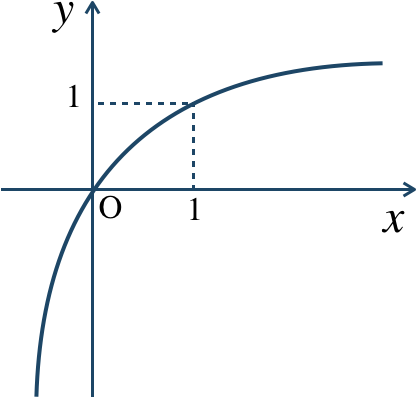
p.180
3
最小値 \(-1\)
3
最小値 \(-1\)
p.180
4
\({\large \frac{ab+3}{ab+a+1}}\)
4
\({\large \frac{ab+3}{ab+a+1}}\)
p.180
5
\(\log_{3}0.5^{1.5}<0<\log_{3}2^{1.5}\)
\(<1<\log_{3}3^{1.5}\)
5
\(\log_{3}0.5^{1.5}<0<\log_{3}2^{1.5}\)
\(<1<\log_{3}3^{1.5}\)
p.180
6
\({\small (1)}~x=1~,~9\)
\({\small (2)}~x=2~,~{\large \frac{1}{4}}\)
6
\({\small (1)}~x=1~,~9\)
\({\small (2)}~x=2~,~{\large \frac{1}{4}}\)
p.180
7
\(n=31\)
7
\(n=31\)
演習問題B
p.180
8
\({\small (1)}~3\) \({\small (2)}~\sqrt{2}\) \({\small (3)}~{\large \frac{1}{2}}\) \({\small (4)}~{\large \frac{1}{4}}\)
8
\({\small (1)}~3\) \({\small (2)}~\sqrt{2}\) \({\small (3)}~{\large \frac{1}{2}}\) \({\small (4)}~{\large \frac{1}{4}}\)
p.180
9
最大値 \(6\)
9
最大値 \(6\)
p.180
10
[証明] 常用対数をとると、$$~~~\log_{10}2^x=\log_{10}3^y=\log_{10}6^z$$よって、$$~~~x\log_{10}2=y\log_{10}3=z\log_{10}6$$これより、$$~~~x=\frac{z\log_{10}6}{\log_{10}2}~,~y=\frac{z\log_{10}6}{\log_{10}3}$$ここで、
(左辺)$$~=\frac{1}{x}+\frac{1}{y}$$$$~=\frac{\log_{10}2}{z\log_{10}6}+\frac{\log_{10}3}{z\log_{10}6}$$$$~=\frac{\log_{10}2+\log_{10}3}{z\log_{10}6}$$$$~=\frac{\log_{10}6}{z\log_{10}6}=\frac{1}{z}$$したがって、$$~~~\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$$[終]
10
[証明] 常用対数をとると、$$~~~\log_{10}2^x=\log_{10}3^y=\log_{10}6^z$$よって、$$~~~x\log_{10}2=y\log_{10}3=z\log_{10}6$$これより、$$~~~x=\frac{z\log_{10}6}{\log_{10}2}~,~y=\frac{z\log_{10}6}{\log_{10}3}$$ここで、
(左辺)$$~=\frac{1}{x}+\frac{1}{y}$$$$~=\frac{\log_{10}2}{z\log_{10}6}+\frac{\log_{10}3}{z\log_{10}6}$$$$~=\frac{\log_{10}2+\log_{10}3}{z\log_{10}6}$$$$~=\frac{\log_{10}6}{z\log_{10}6}=\frac{1}{z}$$したがって、$$~~~\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$$[終]
p.180
11
\({\small (1)}~126\)桁
\({\small (2)}~\)[証明] 常用対数をとると、
\(\log_{10}10^{0.52}=0.52\)
\(\log_{10}4=\log_{10}2^2\)
\(=2\log_{10}2=0.602\)
よって、
\(\log_{10}10^{0.52}<\log_{10}4\)
したがって、
\(10^{0.52<4}\) [終]
\({\small (3)}~3\)
11
\({\small (1)}~126\)桁
\({\small (2)}~\)[証明] 常用対数をとると、
\(\log_{10}10^{0.52}=0.52\)
\(\log_{10}4=\log_{10}2^2\)
\(=2\log_{10}2=0.602\)
よって、
\(\log_{10}10^{0.52}<\log_{10}4\)
したがって、
\(10^{0.52<4}\) [終]
\({\small (3)}~3\)
次のページ「第6章 微分法と積分法」