数研出版：改訂版数学Ｂ

p.7 問1
大きさが等しいベクトル
①と④と⑤と⑦と⑨、③と⑧と⑩

同じ向きのベクトル
①と⑦、②と③と⑩、④と⑨

等しいベクトル
①と⑦、③と⑩、④と⑨
→ ベクトルの基本

p.8 問2
\({\small (1)}~\)

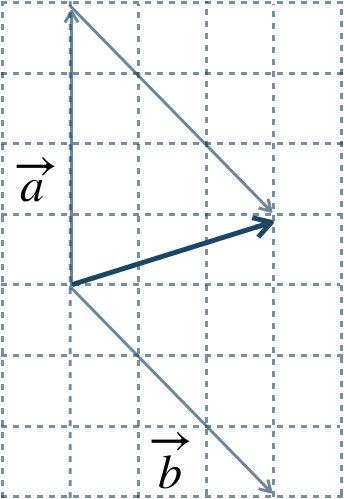
\({\small (2)}~\)

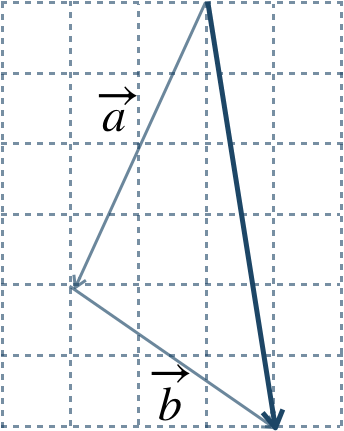
\({\small (3)}~\)

p.9 問3
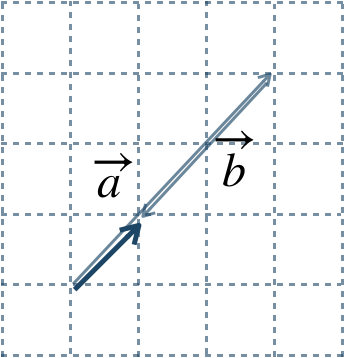
[証明]
\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{\rm OB}\) より、
　\((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\)
\(=\overrightarrow{\rm OB}+\overrightarrow{\rm BC}\)
\(=\overrightarrow{\rm OC}\)

また、\(\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{\rm AC}\) より、
　\(\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\)
\(=\overrightarrow{\rm OA}+\overrightarrow{\rm AC}\)
\(=\overrightarrow{\rm OC}\)

したがって、
　\((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\)
　　　\(=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\)
[終]
→ ベクトルの実数倍・加法・減法

p.10 練習1
\({\small (1)}~\)[証明]
　(左辺)
\(=\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+\overrightarrow{\rm CD}\)
\(=\overrightarrow{\rm AC}+\overrightarrow{\rm CD}\)
\(=\overrightarrow{\rm AD}\)
したがって、
\(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}=\overrightarrow{\rm AD}\)
[終]

\({\small (2)}~\)[証明]
　\(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}+\overrightarrow{\rm DA}\)
\(=(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+(\overrightarrow{\rm CD}+\overrightarrow{\rm DA})\)
\(=\overrightarrow{\rm AC}+\overrightarrow{\rm CA}\)
\(=\overrightarrow{\rm AA}\)
\(=\overrightarrow{0}\)
したがって、
\(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}+\overrightarrow{\rm DA}=\overrightarrow{0}\)
[終]
→ ベクトルの等式証明

p.10 問4
\({\small (1)}~\)

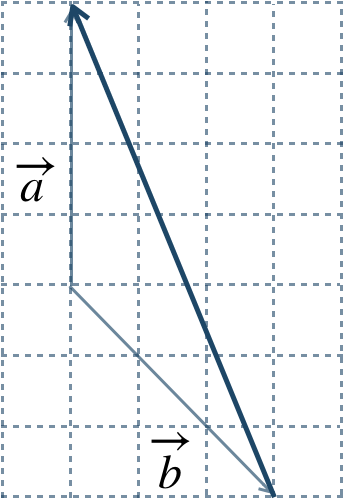
\({\small (2)}~\)

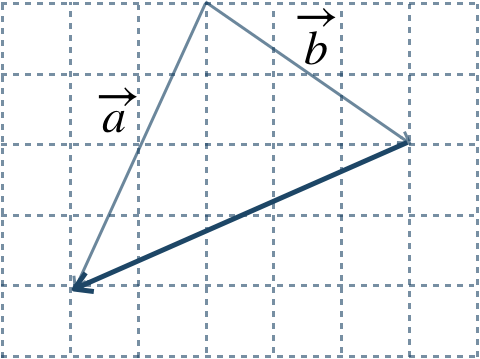
\({\small (3)}~\)

p.10 問5
\({\small (1)}~\overrightarrow{d}-\overrightarrow{b}\)　\({\small (2)}~\overrightarrow{b}-\overrightarrow{d}\)

p.10 練習2
\({\small (1)}~-\overrightarrow{a}\)　\({\small (2)}~\overrightarrow{b}-\overrightarrow{a}\)
\({\small (3)}~-\overrightarrow{a}-\overrightarrow{b}\)
→ ベクトルの実数倍・加法・減法

p.11 練習3
\({\small (1)}~\)

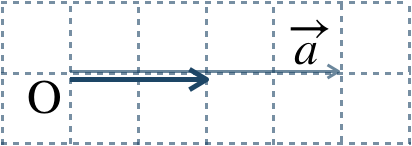
\({\small (2)}~\)

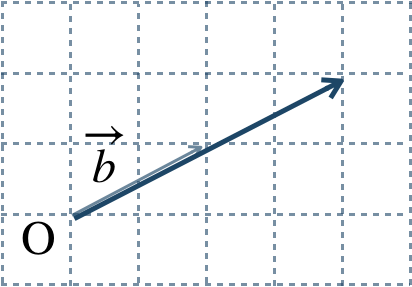
\({\small (3)}~\)

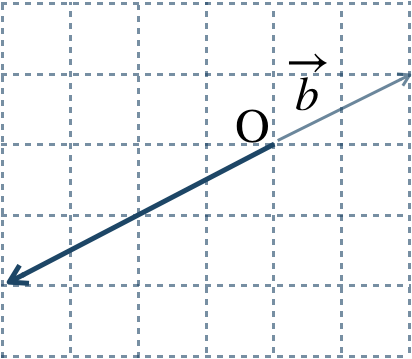
\({\small (4)}~\)

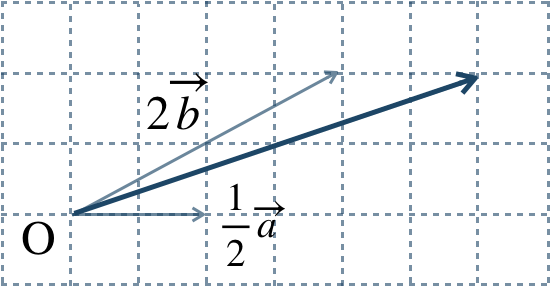
\({\small (5)}~\)

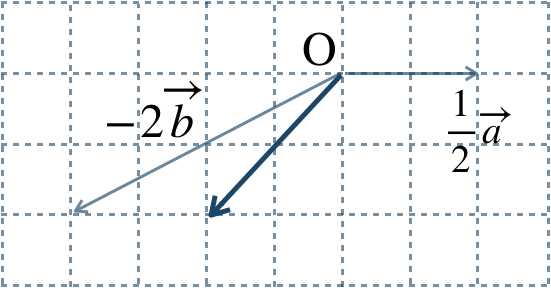
→ ベクトルの実数倍・加法・減法

p.12 問6
[証明] \({\rm AC\parallel A’C’}\) より、\(\triangle {\rm OAC}\sim \triangle {\rm OA’C’}\)
よって、
　\({\rm OC:OC’}=1:k\)
これより、
　\(k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{\rm OC}=\overrightarrow{\rm OC’}\)
また、
\(k\overrightarrow{a}+k\overrightarrow{b}=\overrightarrow{\rm OA’}+\overrightarrow{\rm OB’}=\overrightarrow{\rm OC’}\)
したがって、
\(k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}\)
[終]

p.12 練習4
\({\small (1)}~5\overrightarrow{a}+\overrightarrow{b}\)　\({\small (2)}~-3\overrightarrow{a}+16\overrightarrow{b}\)

p.12 問7
\(\overrightarrow{x}=2\overrightarrow{a}+3\overrightarrow{b}\)

p.12 練習5
\({\small (1)}~\overrightarrow{x}=\overrightarrow{a}+2\overrightarrow{b}\)　\({\small (2)}~\overrightarrow{x}=5\overrightarrow{a}+3\overrightarrow{b}\)
→ ベクトルの演算

p.13 練習6
\({\small (1)}~3\overrightarrow{e}~,~-3\overrightarrow{e}\)　\({\small (2)}~{\large \frac{1}{5}}\overrightarrow{a}~,~-{\large \frac{1}{5}}\overrightarrow{a}\)

p.14 練習7
\(\overrightarrow{\rm AD}=2\overrightarrow{a}+2\overrightarrow{b}~,~\overrightarrow{\rm DF}=-2\overrightarrow{a}-\overrightarrow{b}\)
\(\overrightarrow{\rm CE}=\overrightarrow{b}-\overrightarrow{a}\)
→ ベクトルの分解（正六角形のベクトル）

p.16 練習8
\(\overrightarrow{b}=(2,2)~,~|\overrightarrow{b}|=2\sqrt{2}\)
\(\overrightarrow{c}=(-4,-3)~,~|\overrightarrow{c}|=5\)
\(\overrightarrow{d}=(1,-3)~,~|\overrightarrow{d}|=\sqrt{10}\)
\(\overrightarrow{e}=(-3,0)~,~|\overrightarrow{e}|=3\)

→ ベクトルの成分と大きさ

p.17 練習9
\({\small (1)}~(0,4)\)　\({\small (2)}~(4,-2)\)
\({\small (3)}~(8,4)\)　\({\small (4)}~(10,-7)\)

p.17 練習10
\({\small (1)}~\overrightarrow{p}=3\overrightarrow{a}+2\overrightarrow{b}\)　\({\small (2)}~\overrightarrow{q}=\overrightarrow{a}-3\overrightarrow{b}\)
→ ベクトルの成分と式変形

p.18 練習11
\(x=-3~,~-1\)
→ ベクトルの成分と平行条件

p.19 練習12
\({\small (1)}~\overrightarrow{\rm OB}=(3,5)~,~|\overrightarrow{\rm OB}|=\sqrt{34}\)
\({\small (2)}~\overrightarrow{\rm AB}=(-1,5)~,~|\overrightarrow{\rm AB}|=\sqrt{26}\)
\({\small (3)}~\overrightarrow{\rm BC}=(-5,-10)~,~|\overrightarrow{\rm BC}|=5\sqrt{5}\)
\({\small (4)}~\overrightarrow{\rm CA}=(6,5)~,~|\overrightarrow{\rm CA}|=\sqrt{61}\)
→ 点の座標とベクトルの成分

p.19 練習13
\({\rm E}(-3,-5)\)
→ 平行四辺形とベクトル

p.20 練習14
\({\small (1)}~10\sqrt{3}\)　\({\small (2)}~-10\)　\({\small (3)}~0\)　\({\small (4)}~-20\)
→ ベクトルの内積①（基本）

p.21 問8
\({\small (1)}~3\)　\({\small (2)}~-1\)　\({\small (3)}~0\)

p.21 練習15
\({\small (1)}~1\)　\({\small (2)}~-3\)
→ ベクトルの内積①（基本）

p.22 練習16
\({\small (1)}~-1\)　\({\small (2)}~0\)
→ ベクトルの内積②（成分利用）

p.23 練習17
\({\small (1)}~30^\circ\)　\({\small (2)}~135^\circ\)
→ ベクトルのなす角

p.24 練習18
\(\overrightarrow{e}=\left({\large \frac{1}{\sqrt{5}}},{\large \frac{2}{\sqrt{5}}}\right)~,~\left(-{\large \frac{1}{\sqrt{5}}},-{\large \frac{2}{\sqrt{5}}}\right)\)
→ ベクトルの垂直条件

p.24 練習19
\({\small (1)}~\)[証明] 内積を計算すると、
　\(\overrightarrow{a}\cdot\overrightarrow{b}=a_1a_2+a_2(-a_1)=0\)
また、\(\overrightarrow{a}\neq\overrightarrow{0}\) かつ \(\overrightarrow{b}\neq\overrightarrow{0}\) より、
\(\overrightarrow{a}\) と \(\overrightarrow{b}\) は垂直である [終]

\({\small (2)}~\)
\(\overrightarrow{e}=\left({\large \frac{2}{\sqrt{13}}},-{\large \frac{3}{\sqrt{13}}}\right)~,~\left(-{\large \frac{2}{\sqrt{13}}},{\large \frac{3}{\sqrt{13}}}\right)\)
→ ベクトルの垂直条件

p.25 問9
[証明] 性質１
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) とすると、
　\(\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2\)
また、
　\(\overrightarrow{b}\cdot\overrightarrow{a}=b_1a_1+b_2a_2\)
　　　　　\(=a_1b_1+a_2b_2\)
したがって、
\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{a}\)
[終]

[証明] 性質２
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) とすると、
\(k\overrightarrow{a}=(ka_1,ka_2)~,~k\overrightarrow{b}=(kb_1,kb_2)\)
よって、
　\((k\overrightarrow{a})\cdot\overrightarrow{b}=ka_1b_1+ka_2b_2\)
また、
　\(\overrightarrow{a}\cdot(k\overrightarrow{b})=a_1kb_1+a_2kb_2\)
　　　　　　\(=ka_1b_1+ka_2b_2\)
また、
　\(\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2\)
これより、
　\(k(\overrightarrow{a}\cdot\overrightarrow{b})=k(a_1b_1+a_2b_2)\)
　　　　　　\(=ka_1b_1+ka_2b_2\)
したがって、
\((k\overrightarrow{a})\cdot\overrightarrow{b}=\overrightarrow{a}\cdot(k\overrightarrow{b})=k(\overrightarrow{a}\cdot\overrightarrow{b})\)
[終]

p.25 問10
[証明] 性質１
\(\overrightarrow{a}\) と \(\overrightarrow{a}\) のなす角が \(0^\circ\) であるので、内積を計算すると、
　\(\overrightarrow{a}\cdot\overrightarrow{a}=|\overrightarrow{a}||\overrightarrow{a}|\cos{0^\circ}=|\overrightarrow{a}|^2\)
したがって、
　\(\overrightarrow{a}\cdot\overrightarrow{a}=|\overrightarrow{a}|^2\) [終]

[証明] 性質２
\(\overrightarrow{a}\cdot\overrightarrow{a}=|\overrightarrow{a}|^2\) より、\(|\overrightarrow{a}|≧0\) であるので、
　\(|\overrightarrow{a}|=\sqrt{\overrightarrow{a}\cdot\overrightarrow{a}}\) [終]

p.25 練習20
\({\small (1)}~\)[証明]
　(左辺)
\(=(2\overrightarrow{a}+3\overrightarrow{b})\cdot(\overrightarrow{c}-2\overrightarrow{d})\)
\(=2\overrightarrow{a}\cdot(\overrightarrow{c}-2\overrightarrow{d})\)
　　　　　\(+3\overrightarrow{b}(\overrightarrow{c}-2\overrightarrow{d})\)
\(=2\overrightarrow{a}\cdot\overrightarrow{c}-4\overrightarrow{a}\cdot\overrightarrow{d}\)
　　　　\(+3\overrightarrow{b}\cdot\overrightarrow{c}-6\overrightarrow{b}\cdot\overrightarrow{d}\)
したがって、
\((2\overrightarrow{a}+3\overrightarrow{b})\cdot(\overrightarrow{c}-2\overrightarrow{d})\)
　\(=2\overrightarrow{a}\cdot\overrightarrow{c}-4\overrightarrow{a}\cdot\overrightarrow{d}\)
　　　　　\(+3\overrightarrow{b}\cdot\overrightarrow{c}-6\overrightarrow{b}\cdot\overrightarrow{d}\)
[終]

\({\small (2)}~\)[証明]
　(左辺)
\(=|2\overrightarrow{a}-3\overrightarrow{b}|^2\)
\(=(2\overrightarrow{a}-3\overrightarrow{b})\cdot(2\overrightarrow{a}-3\overrightarrow{b})\)
\(=2\overrightarrow{a}\cdot(2\overrightarrow{a}-3\overrightarrow{b})\)
　　　\(-3\overrightarrow{b}(2\overrightarrow{a}-3\overrightarrow{b})\)
\(=4\overrightarrow{a}\cdot\overrightarrow{a}-6\overrightarrow{a}\cdot\overrightarrow{b}\)
　　　\(-6\overrightarrow{b}\cdot\overrightarrow{a}+9\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=4|\overrightarrow{a}|^2-12\overrightarrow{a}\cdot\overrightarrow{b}+9|\overrightarrow{b}|^2\)
したがって、
\(|2\overrightarrow{a}-3\overrightarrow{b}|^2\)
　　\(=4|\overrightarrow{a}|^2-12\overrightarrow{a}\cdot\overrightarrow{b}+9|\overrightarrow{b}|^2\)
[終]
→ 内積を用いた等式証明

p.26 練習21
\(2\sqrt{7}\)
→ 内積の性質の利用（ベクトルの大きさと内積）

p.26 練習22
\(\overrightarrow{a}\cdot\overrightarrow{b}=-{\large \frac{3}{2}}~,~150^\circ\)
→ 内積の性質の利用（ベクトルの大きさと内積）

p.27
研究1
\({\small (1)}~5\)　\({\small (2)}~{\large \frac{11}{2}}\)
→ ベクトルと三角形の面積

p.28 1
[証明]
\(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}+\overrightarrow{\rm DE}\)
　　　　　\(+\overrightarrow{\rm EF}+\overrightarrow{\rm FA}=\overrightarrow{0}\)
であり、\(\overrightarrow{\rm AB}=\overrightarrow{\rm ED}~,~\overrightarrow{\rm BC}=\overrightarrow{\rm FE}\) より、
\(\overrightarrow{\rm ED}+\overrightarrow{\rm FE}+\overrightarrow{\rm CD}+\overrightarrow{\rm DE}\)
　　　　　\(+\overrightarrow{\rm EF}+\overrightarrow{\rm FA}=\overrightarrow{0}\)
また、\(\overrightarrow{\rm ED}+\overrightarrow{\rm DE}=\overrightarrow{0}\) かつ \(\overrightarrow{\rm FE}+\overrightarrow{\rm EF}=\overrightarrow{0}\) より、
　\(\overrightarrow{\rm CD}+\overrightarrow{\rm FA}=\overrightarrow{0}\)
　　　\(~\Leftrightarrow~\overrightarrow{\rm CD}=\overrightarrow{\rm AF}\)
したがって、\({\rm CD}\) と \({\rm AF}\) は平行で \({\rm CD=AF}\)
[終]

p.28 2
\(\overrightarrow{a}=\left({\large \frac{1}{2}},{\large \frac{1}{2}}\right)~,~\overrightarrow{b}=\left({\large \frac{1}{2}},{\large \frac{3}{2}}\right)\)
\(|2\overrightarrow{a}-3\overrightarrow{b}|={\large \frac{5\sqrt{2}}{2}}\)

p.28 3
\(t={\large \frac{4}{5}}\) で最小値 \({\large \frac{7\sqrt{5}}{5}}\)

p.28 4
\({\small (1)}~-2\)　\({\small (2)}~2\)　\({\small (3)}~4\)
\({\small (4)}~8\)　\({\small (5)}~0\)　\({\small (6)}~6\)

p.28 5
[証明]
ベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) のなす角を \(\theta\) とすると、
　\(\overrightarrow{a}\parallel\overrightarrow{b}\)
\(~\Leftrightarrow~\theta=0^\circ\) または \(\theta=180^\circ\)
\(~\Leftrightarrow~\cos{\theta}=1\) または \(\cos{\theta}=-1\)
\(~\Leftrightarrow~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\)
　　　または \(\overrightarrow{a}\cdot\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)
よって、\(|\overrightarrow{a}\cdot\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|\)
\(|\overrightarrow{a}\cdot\overrightarrow{b}|≧0~,~|\overrightarrow{a}|≧0~,~|\overrightarrow{b}|≧0\) であるので、
　\(|\overrightarrow{a}\cdot\overrightarrow{b}|^2=|\overrightarrow{a}|^2|\overrightarrow{b}|^2\)
それぞれの成分より、
　\((a_1b_1+a_2b_2)^2=(a_1^2+a_2^2)(b_1^2+b_2^2)\)
展開して計算すると、
　\((a_1b_2-a_2b_1)^2=0\)
よって、
　\(a_1b_2-a_2b_1=0\)
したがって、\(\overrightarrow{a}\neq\overrightarrow{0}~,~\overrightarrow{b}\neq\overrightarrow{0}\) で、
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) のとき、
　\(\overrightarrow{a}\parallel\overrightarrow{b}~\Leftrightarrow~a_1b_2-a_2b_1=0\) [終]

\(p=-3~,~1\)

p.28 6
\({\small (1)}~\)[証明]
　(左辺)
\(=|\overrightarrow{a}+\overrightarrow{b}|^2+|\overrightarrow{a}-\overrightarrow{b}|^2\)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}+\overrightarrow{b})\)
　　　\(+(\overrightarrow{a}-\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=(|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2)\)
　　　\(+(|\overrightarrow{a}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2)\)
\(=2(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2)\)
したがって、
\(|\overrightarrow{a}+\overrightarrow{b}|^2+|\overrightarrow{a}-\overrightarrow{b}|^2\)
　　\(=2(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2)\)
[終]

\({\small (2)}~\)[証明]
　(左辺)
\(=|\overrightarrow{a}+\overrightarrow{b}|^2-|\overrightarrow{a}-\overrightarrow{b}|^2\)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}+\overrightarrow{b})\)
　　　\(-(\overrightarrow{a}-\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=(|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2)\)
　　　\(-(|\overrightarrow{a}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2)\)
\(=4\overrightarrow{a}\cdot\overrightarrow{b}\)
したがって、
\(|\overrightarrow{a}+\overrightarrow{b}|^2-|\overrightarrow{a}-\overrightarrow{b}|^2\)
　　\(=4\overrightarrow{a}\cdot\overrightarrow{b}\)
[終]

p.28 7
\({\small (1)}~-{\large \frac{1}{3}}\)　\({\small (2)}~{\large \frac{15}{7}}\)

p.30 問11
[証明]
\(\overrightarrow{\rm BQ}={\large \frac{n}{n-m}}\overrightarrow{\rm BA}\) であるので、
　\(\overrightarrow{q}-\overrightarrow{b}={\large \frac{n}{n-m}}(\overrightarrow{a}-\overrightarrow{b})\)
　　\(~\Leftrightarrow~\overrightarrow{q}={\large \frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}}\)
[終]

p.31 問12
\({\small (1)}~{\large \frac{1}{3}}\overrightarrow{a}+{\large \frac{2}{3}}\overrightarrow{b}\)　\({\small (2)}~{\large \frac{2}{3}}\overrightarrow{a}+{\large \frac{1}{3}}\overrightarrow{b}\)
\({\small (3)}~-\overrightarrow{a}+2\overrightarrow{b}\)　\({\small (4)}~2\overrightarrow{a}-\overrightarrow{b}\)

p.31 練習23
\({\small (1)}~{\large \frac{2}{5}}\overrightarrow{a}+{\large \frac{3}{5}}\overrightarrow{b}\)　\({\small (2)}~{\large \frac{3}{2}}\overrightarrow{a}-{\large \frac{1}{2}}\overrightarrow{b}\)
→ 内分点・外分点の位置ベクトル

p.32 練習24
\({\small (1)}~\)[証明]
\({\rm A,B,C,G,P,Q,R,G’}\) の位置ベクトルをそれぞれ
　\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{g},\overrightarrow{p},\overrightarrow{q},\overrightarrow{r},\overrightarrow{g’}\)
とすると、\(\triangle {\rm ABC}\) の重心は、
　\(\overrightarrow{g}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
\(\triangle {\rm PQR}\) の重心は、
　\(\overrightarrow{g’}={\large \frac{\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}}{3}}\)
また、\({\rm P~,~Q~,~R}\) はそれぞれ
　\(\overrightarrow{p}={\large \frac{2\overrightarrow{b}+\overrightarrow{c}}{3}}~,~\overrightarrow{q}={\large \frac{2\overrightarrow{c}+\overrightarrow{a}}{3}}\)
　\(\overrightarrow{r}={\large \frac{2\overrightarrow{a}+\overrightarrow{b}}{3}}\)
これを代入すると、
　\(\overrightarrow{g’}={\large \frac{1}{3}}\cdot{\large \frac{3\overrightarrow{a}+3\overrightarrow{b}+3\overrightarrow{c}}{3}}\)
よって、
　\(\overrightarrow{g’}={\large \frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}}\)
\(\overrightarrow{g}=\overrightarrow{g’}\) より、\({\rm G}\) と \({\rm G’}\) は一致する [終]

\({\small (2)}~\)[証明]
　(左辺)
\(=\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}\)
\(=(\overrightarrow{a}-\overrightarrow{g})+(\overrightarrow{b}-\overrightarrow{g})+(\overrightarrow{c}-\overrightarrow{g})\)
\(=(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-3\overrightarrow{g}\)
ここで、\(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=3\overrightarrow{g}\) より、
\(=3\overrightarrow{g}-3\overrightarrow{g}=\overrightarrow{0}\)
したがって、
\(\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}\)
[終]
→ 重心の位置ベクトル

p.33 練習25
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とすると
点 \({\rm E}\) は辺 \({\rm BC}\) を \(4:1\) に内分するので、
　\(\overrightarrow{\rm AE}={\large \frac{\overrightarrow{b}+4\overrightarrow{c}}{5}}\)
また、\(\overrightarrow{\rm AD}={\large \frac{1}{3}}\overrightarrow{b}\) で、点 \({\rm F}\) は辺 \({\rm CD}\) を \(3:4\) に内分するので、
　\(\overrightarrow{\rm AF}={\large \frac{3\cdot{\large \frac{1}{3}}\overrightarrow{b}+4\overrightarrow{c}}{7}}={\large \frac{\overrightarrow{b}+4\overrightarrow{c}}{7}}\)
よって、
　\(\overrightarrow{\rm AF}={\large \frac{\overrightarrow{b}+4\overrightarrow{c}}{7}}={\large \frac{5}{7}}\cdot{\large \frac{\overrightarrow{b}+4\overrightarrow{c}}{5}}\)
これより、
　\(\overrightarrow{\rm AF}={\large \frac{5}{7}}\overrightarrow{\rm AE}\)
したがって、３点 \({\rm A~,~F~,~E}\) は一直線上にある [終]
→ ３点が同一直線上にある条件

p.34 練習26
\(\overrightarrow{\rm OP}={\large \frac{1}{3}}\overrightarrow{a}+{\large \frac{4}{9}}\overrightarrow{b}\)
→ ２直線の交点とベクトル

p.35 練習27
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とすると、
\({\rm AB=AC}\) より
　 \(|\overrightarrow{b}|=|\overrightarrow{c}|\)
また、\({\rm AB\perp AC}\) より
　 \(\overrightarrow{b}\cdot\overrightarrow{c}=0\)
次に、点 \({\rm L}\) は辺 \({\rm BC}\) を \(2:1\) に内分するので、
　\(\overrightarrow{\rm AL}={\large \frac{1}{3}}\overrightarrow{b}+{\large \frac{2}{3}}\overrightarrow{c}\)
また、
　\(\overrightarrow{\rm MN}=\overrightarrow{\rm AN}-\overrightarrow{\rm AM}\)
これより、
　\(\overrightarrow{\rm MN}={\large \frac{2}{3}}\overrightarrow{b}-{\large \frac{1}{3}}\overrightarrow{c}\)
よって、
　\(\overrightarrow{\rm AL}\cdot\overrightarrow{\rm MN}\)
\(=\left({\large \frac{1}{3}}\overrightarrow{b}+{\large \frac{2}{3}}\overrightarrow{c}\right)\left({\large \frac{2}{3}}\overrightarrow{b}-{\large \frac{1}{3}}\overrightarrow{c}\right)\)
\(={\large \frac{2}{9}}|\overrightarrow{b}|^2-{\large \frac{2}{9}}|\overrightarrow{c}|^2+{\large \frac{1}{3}}\overrightarrow{b}\cdot\overrightarrow{c}\)
\(=0\)
内積が \(0\) となり、
\(\overrightarrow{\rm AL}\neq\overrightarrow{0}~,~\overrightarrow{\rm MN}\neq\overrightarrow{0}\)
であるので、
　\(\overrightarrow{\rm AL}\perp\overrightarrow{\rm MN}\)
したがって、
　\({\rm AL\perp MN}\)
[終]

p.37 練習28
\({\small (1)}~\)\(\biggl\{ \begin{eqnarray} x=3+4t \\ y=2+5t \end{eqnarray}~,~5x-4y-7=0\)
\({\small (2)}~\)\(\biggl\{ \begin{eqnarray} x=1-2t \\ y=-2+3t \end{eqnarray}~,~3x+2y+1=0\)

p.38 問13
\({\small (1)}~\)\(\biggl\{ \begin{eqnarray} x=3-5t \\ y=-2+4t \end{eqnarray}\)　\({\small (2)}~\)\(\biggl\{ \begin{eqnarray} x=4-4t \\ y=5t \end{eqnarray}\)
→ 直線のベクトル方程式

p.39 練習29
\(\overrightarrow{\rm OA’}={\large \frac{1}{2}}\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}={\large \frac{1}{2}}\overrightarrow{\rm OB}\) となる点を
\({\rm A’~,~B’}\) とすると、線分 \({\rm A’B’}\)
→ ベクトルと点の存在範囲

p.40 問14
\(\overrightarrow{\rm OA’}=2\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}=2\overrightarrow{\rm OB}\) となる点を
\({\rm A’~,~B’}\) とすると、\({\rm \triangle {\rm OA’B’}}\) の周と内部
→ ベクトルと点の存在範囲

p.40 練習30
\({\small (1)}~\)
\(\overrightarrow{\rm OA’}=3\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}=3\overrightarrow{\rm OB}\) となる点を
\({\rm A’~,~B’}\) とすると、\({\rm \triangle {\rm OA’B’}}\) の周と内部
\({\small (2)}~\)
\(\overrightarrow{\rm OA’}={\large \frac{1}{2}}\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB’}={\large \frac{1}{2}}\overrightarrow{\rm OB}\) となる点を
\({\rm A’~,~B’}\) とすると、\({\rm \triangle {\rm OA’B’}}\) の周と内部
→ ベクトルと点の存在範囲

p.42 練習31
\({\small (1)}~5x+2y-16=0\)
\({\small (2)}~3x-5y+13=0\)
→ 法線ベクトル

p.42 問15
\({\small (1)}~120^\circ\)　\({\small (2)}~60^\circ\)

p.42 練習32
\(45^\circ\)

p.43 練習33
\({\small (1)}~\)中心 \(2\overrightarrow{a}\)、半径 \(1\)
\({\small (2)}~\)中心 \({\large \frac{1}{3}}\overrightarrow{a}\)、半径 \(2\)
→ 円のベクトル方程式

p.43 練習34
\({\small (1)}~\)[証明]
円の中心は線分 \({\rm AB}\) の中点となり、位置ベクトルは、
　\({\large \frac{\overrightarrow{a}+\overrightarrow{b}}{2}}\)
また、この円の直径が \(|\overrightarrow{a}-\overrightarrow{b}|\) より、半径は、
　\({\large \frac{|\overrightarrow{a}-\overrightarrow{b}|}{2}}\)
したがって、円のベクトル方程式は、
　\(\left|\overrightarrow{p}-{\large \frac{\overrightarrow{a}+\overrightarrow{b}}{2}}\right|={\large \frac{|\overrightarrow{a}-\overrightarrow{b}|}{2}}\)
[終]

\({\small (2)}~\)[証明]
(1) の式の両辺を２乗すると、
\(\left|\overrightarrow{p}-{\large \frac{\overrightarrow{a}+\overrightarrow{b}}{2}}\right|^2={\large \frac{|\overrightarrow{a}-\overrightarrow{b}|^2}{2^2}}\)
両辺に \(\times4\) すると、
　\(|2\overrightarrow{p}-(\overrightarrow{a}+\overrightarrow{b})|^2=|\overrightarrow{a}-\overrightarrow{b}|^2\)
これを展開し、整理すると、
　\(|\overrightarrow{p}|^2-(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{p}+\overrightarrow{a}\cdot\overrightarrow{b}=0\)
因数分解すると、
　\((\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{b})=0\)
[終]

p.43 練習35
[証明]
(ⅰ) \({\rm A}\) と \({\rm P}\) が一致するとき、
　\(\overrightarrow{\rm AP}=\overrightarrow{0}\)
よって、
　\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)

(ⅱ) \({\rm A}\) と \({\rm P}\) が一致しないとき、
　\(\overrightarrow{\rm AP}\perp\overrightarrow{\rm CA}\)
よって、
　\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)

これらより、いずれの場合でも
　\((\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})=0\) …①
次に、\(|\overrightarrow{\rm CA}|=r\) より、
　\(|\overrightarrow{a}-\overrightarrow{c}|^2=r^2\)
また、
　\((\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\) …②
よって、①＋②より
　\((\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})\)
　　　　\(+(\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
　\((\overrightarrow{p}-\overrightarrow{a}+\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
　\((\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
したがって、接線のベクトル方程式は、
　\((\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\) [終]