文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
1章 方程式・式と証明
2章 図形と方程式
3章 三角関数
4章 指数関数・対数関数
5章 微分と積分
4章 指数関数・対数関数
1節 指数関数
p.158 問1$${\small (1)}~{ \frac{1}{\,5\,}}$$$${\small (2)}~1$$$${\small (3)}~{ \frac{1}{\,100\,}}$$$${\small (4)}~-{ \frac{1}{\,64\,}}$$
p.158 問2$${\small (1)}~a^{-1}$$$${\small (2)}~a^0$$$${\small (3)}~a^{-5}$$$${\small (4)}~a^{-17}$$
p.159 問3$${\small (1)}~a^3$$$${\small (2)}~{ \frac{1}{\,x^4\,}}$$$${\small (3)}~{ \frac{\,b^8\,}{\,a^6\,}}$$$${\small (4)}~x^{10}y^{15}$$→ 指数法則の基本
p.160 問4$${\small (1)}~5$$$${\small (2)}~-5$$$${\small (3)}~4$$$${\small (4)}~-3$$
p.161 問5\({\small (1)}~\)[証明] \(\left({\sqrt[\large n]{a}}\right)^m=x\) とすると、
\(x^n\)
\(=\left\{\left({\sqrt[\large n]{a}}\right)^m\right\}^n\)
\(=\left\{\left({\sqrt[\large n]{a}}\right)^n\right\}^m\)
\(=a^m\)
ここで、\(x>0\) であり、\(x\) は \(a^m\) の正の \(n\) 乗根であるので、
\(x=\sqrt[\large n]{a^m}\)
したがって、
\(\left({\sqrt[\large n]{a}}\right)^m=\sqrt[\large n]{a^m}\) [終]
\({\small (2)}~\)[証明] \(\sqrt[\large m]{\sqrt[\large n]{a}}=x\) とすると、
\(x^{mn}\)
\(=(\sqrt[\large m]{\sqrt[\large n]{a}})^{mn}\)
\(=\left\{(\sqrt[\large m]{\sqrt[\large n]{a}})^m\right\}^n\)
\(=(\sqrt[\large n]{a})^n\)
\(=a\)
ここで、\(x>0\) であり、\(x\) は \(a\) の正の \(mn\) 乗根であるので、
\(x=\sqrt[\large mn]{a}\)
したがって、
\(\sqrt[\large m]{\sqrt[\large n]{a}}=\sqrt[\large mn]{a}\) [終]
\(x^n\)
\(=\left\{\left({\sqrt[\large n]{a}}\right)^m\right\}^n\)
\(=\left\{\left({\sqrt[\large n]{a}}\right)^n\right\}^m\)
\(=a^m\)
ここで、\(x>0\) であり、\(x\) は \(a^m\) の正の \(n\) 乗根であるので、
\(x=\sqrt[\large n]{a^m}\)
したがって、
\(\left({\sqrt[\large n]{a}}\right)^m=\sqrt[\large n]{a^m}\) [終]
\({\small (2)}~\)[証明] \(\sqrt[\large m]{\sqrt[\large n]{a}}=x\) とすると、
\(x^{mn}\)
\(=(\sqrt[\large m]{\sqrt[\large n]{a}})^{mn}\)
\(=\left\{(\sqrt[\large m]{\sqrt[\large n]{a}})^m\right\}^n\)
\(=(\sqrt[\large n]{a})^n\)
\(=a\)
ここで、\(x>0\) であり、\(x\) は \(a\) の正の \(mn\) 乗根であるので、
\(x=\sqrt[\large mn]{a}\)
したがって、
\(\sqrt[\large m]{\sqrt[\large n]{a}}=\sqrt[\large mn]{a}\) [終]
p.161 問6$${\small (1)}~10$$$${\small (2)}~2$$$${\small (3)}~\sqrt{6}$$$${\small (4)}~2\sqrt[\large 3]{2}$$→ 累乗根
p.162 問7$${\small (1)}~2$$$${\small (2)}~81$$$${\small (3)}~{ \frac{1}{\,6\,}}$$$${\small (4)}~{ \frac{1}{\,25\,}}$$
p.162 問8$${\small (1)}~a^{\large \frac{1}{5}}$$$${\small (2)}~a^{\large \frac{5}{3}}$$$${\small (3)}~a^{-\large \frac{3}{2}}$$$${\small (4)}~a^{-{\large \frac{7}{3}}}$$→ 指数法則の拡張
p.163 問9$${\small (1)}~7$$$${\small (2)}~{ \frac{1}{\,2\,}}$$$${\small (3)}~{ \frac{\,5\,}{3}}$$
p.163 問10$${\small (1)}~\sqrt[\large 8]{a}$$$${\small (2)}~\sqrt{b}$$→ 指数法則を用いた計算
p.164 問11$$~~~2^{-{\large \frac{5}{2}}}=\frac{\,\sqrt{2}\,}{\,8\,}≒0.18$$$$~~~2^{{\large \frac{5}{2}}}=4\sqrt{2}≒5.66$$
p.164 問12
p.166 問14$${\small (1)}~\sqrt[\large 3]{9}<\sqrt[\large7 ]{283}<\sqrt[\large 5]{81}$$$${\small (2)}~\sqrt[\large 4]{{ \frac{1}{\,8\,}}}<\sqrt[\large 3]{{ \frac{1}{\,4\,}}}<\sqrt{{ \frac{1}{\,2\,}}}$$→ 指数の大小比較
p.167 問15

p.168 問16$${\small (1)}~x={ \frac{2}{\,3\,}}$$$${\small (2)}~x=-2$$$${\small (3)}~x=\frac{\,6\,}{\,7\,}$$→ 指数方程式
p.168 問17$${\small (1)}~x=0$$$${\small (2)}~x=-1~,~2$$→ 指数関数を含む2次方程式
p.170 問題 6\({\small (1)}~\)\(y=2^x\) のグラフを \(x\) 軸方向に \(1\) だけ平行移動したグラフ
\({\small (2)}~\)\(y=2^x\) のグラフを \(y\) 軸で対称移動させて、\(y\) 軸方向に \(1\) だけ平行移動したグラフ
\({\small (2)}~\)\(y=2^x\) のグラフを \(y\) 軸で対称移動させて、\(y\) 軸方向に \(1\) だけ平行移動したグラフ
2節 対数関数
p.172 問1$$~~~\log_{2}{3}~,~\log_{2}{4}~,~\log_{2}{5}$$
p.172 問2$${\small (1)}~\log_{3}9=2$$$${\small (2)}~\log_{5}125=3$$$${\small (3)}~\log_{2}{ \frac{1}{\,4\,}}=-2$$→ 指数と対数
p.172 問3$${\small (1)}~3^4=81$$$${\small (2)}~25^{{ \frac{1}{\,2\,}}}=5$$$${\small (3)}~2^{-4}={ \frac{1}{\,16\,}}$$
p.173 問4$${\small (1)}~2$$$${\small (2)}~0$$$${\small (3)}~1$$→ 対数の値
p.173 問5\(\log_{a}M=p~,~\log_{a}N=q\) とすると、
\(M=a^p~,~N=a^q\)
\(N\neq0\) より、
\({\large \frac{M}{N}}={\large \frac{a^p}{a^q}}=a^{p-q}\)
対数の定義より、
\(\log_{a}{\large \frac{M}{N}}=p-q\)
したがって、
\(\log_{a}{\large \frac{M}{N}}=\log_{a}M-\log_{a}N\) [終]
\(M=a^p~,~N=a^q\)
\(N\neq0\) より、
\({\large \frac{M}{N}}={\large \frac{a^p}{a^q}}=a^{p-q}\)
対数の定義より、
\(\log_{a}{\large \frac{M}{N}}=p-q\)
したがって、
\(\log_{a}{\large \frac{M}{N}}=\log_{a}M-\log_{a}N\) [終]
p.173 問6[証明]$$~~~\log_{a}{\frac{\,1\,}{\,N\,}}=\log_{a}{1}-\log_{a}{N}$$\(\log_{a}{1}=0\) より、$$~~~\log_{a}{\frac{\,1\,}{\,N\,}}=-\log_{a}{N}$$[終]
[証明]$$~~~\log_{a}{\sqrt[\large n]{M}}=\log_{a}{M^{\frac{\,1\,}{\,n\,}}}$$したがって、$$~~~\log_{a}{\sqrt[\large n]{M}}=\frac{\,1\,}{\,n\,}\log_{a}{M}$$[終]
[証明]$$~~~\log_{a}{\sqrt[\large n]{M}}=\log_{a}{M^{\frac{\,1\,}{\,n\,}}}$$したがって、$$~~~\log_{a}{\sqrt[\large n]{M}}=\frac{\,1\,}{\,n\,}\log_{a}{M}$$[終]
p.174 問7$${\small (1)}~2$$$${\small (2)}~3$$$${\small (3)}~-1$$$${\small (4)}~-{ \frac{1}{\,2\,}}$$→ 対数の計算
p.174 問8$${\small (1)}~-3p-2q$$$${\small (2)}~{ \frac{1}{\,2\,}}(q-1)$$$${\small (3)}~-2p+q+2$$
p.175 問9$${\small (1)}~{ \frac{\,4\,}{3}}$$$${\small (2)}~{ \frac{3}{\,4\,}}$$$${\small (3)}~-{ \frac{\,5\,}{2}}$$→ 対数関数の式の値
p.175 問10$${\small (1)}~-2$$$${\small (2)}~2$$$${\small (3)}~{ \frac{1}{\,3\,}}$$→ 底の変換公式
p.178 問12\(x\) 軸で対称

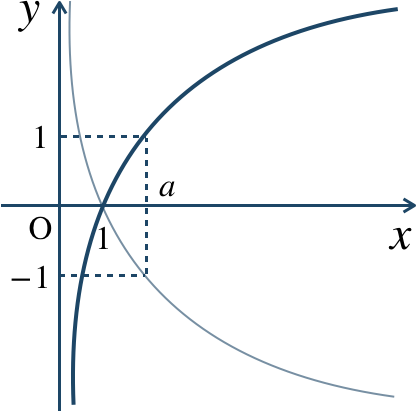
p.178 問13$${\small (1)}~\log_{4}\sqrt{7}<\log_{4}\sqrt{8}<\log_{4}3$$$${\small (2)}~\log_{0.5}5<\log_{0.5}2<\log_{0.5}0.1$$→ 対数の大小比較
p.179 問14$${\small (1)}~x=11$$$${\small (2)}~x=-{ \frac{8}{\,9\,}}$$
p.179 問15$${\small (1)}~x=5$$$${\small (2)}~x=1$$→ 対数方程式
p.179 問16$$~~~x=1~,~10$$
p.180 問17$${\small (1)}~-2<x≦7$$$${\small (2)}~x<-6$$
p.180 問18$${\small (1)}~4<x<8$$$${\small (2)}~1<x≦3$$→ 対数不等式
p.182 問20$$~~~2.0792$$
p.183 問23 \(12\) 回
p.184 問題 18[証明] 底の変換公式より、
(左辺)
\(=\log_{a}b\cdot{\large \frac{\log_{a}c}{\log_{a}b}}\cdot{\large \frac{\log_{a}a}{\log_{a}c}}=1\)
したがって、
\(\log_{a}b\cdot\log_{b}c\cdot\log_{c}a=1\)
[終]
(左辺)
\(=\log_{a}b\cdot{\large \frac{\log_{a}c}{\log_{a}b}}\cdot{\large \frac{\log_{a}a}{\log_{a}c}}=1\)
したがって、
\(\log_{a}b\cdot\log_{b}c\cdot\log_{c}a=1\)
[終]
練習問題 指数関数・対数関数
p.186 練習問題A 7[証明]
\(2^7=128~,~2^8=256~,~3^5=243\) より、
\(2^7<3^5<2^8\)
底が \(2\) の対数をとると、
\(7<5\log_{2}3<8\)
それぞれの辺を \(5\) で割ると、
\(1.4<\log_{2}3<1.6\) [終]
\(2^7=128~,~2^8=256~,~3^5=243\) より、
\(2^7<3^5<2^8\)
底が \(2\) の対数をとると、
\(7<5\log_{2}3<8\)
それぞれの辺を \(5\) で割ると、
\(1.4<\log_{2}3<1.6\) [終]
p.187 練習問題B 10[証明]
\(a^{\log_{a}M}=x\) として、両辺に底が \(a\) の対数をとると、
\(\log_{a}a^{\log_{a}M}=\log_{a}x\)
\(~\Leftrightarrow~\log_{a}M\cdot\log_{a}a=\log_{a}x\)
\(~\Leftrightarrow~\log_{a}M=\log_{a}x\)
よって、\(x=M\) となり、
\(a^{\log_{a}M}=M\) [終]
$${\small (1)}~27$$$${\small (2)}~{ \frac{1}{\,16\,}}$$$${\small (3)}~{ \frac{1}{\,9\,}}$$
\(a^{\log_{a}M}=x\) として、両辺に底が \(a\) の対数をとると、
\(\log_{a}a^{\log_{a}M}=\log_{a}x\)
\(~\Leftrightarrow~\log_{a}M\cdot\log_{a}a=\log_{a}x\)
\(~\Leftrightarrow~\log_{a}M=\log_{a}x\)
よって、\(x=M\) となり、
\(a^{\log_{a}M}=M\) [終]
$${\small (1)}~27$$$${\small (2)}~{ \frac{1}{\,16\,}}$$$${\small (3)}~{ \frac{1}{\,9\,}}$$
p.187 練習問題B 14[証明] \(2^x=5^y=10^z=t\) とすると、
\(x=\log_{2}t\)
\(y=\log_{5}t={\large \frac{\log_{2}t}{\log_{2}5}}\)
\(z=\log_{10}t={\large \frac{\log_{2}t}{\log_{2}10}}\)
ここで、
\({\large \frac{1}{x}}+{\large \frac{1}{y}}\)
\(={\large \frac{1}{\log_{2}t}}+{\large \frac{\log_{2}5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}2+\log_{2}5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}2\times5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}10}{\log_{2}t}}\)
\(={\large \frac{1}{z}}\)
したがって、
\({\large \frac{1}{x}}+{\large \frac{1}{y}}={\large \frac{1}{z}}\) [終]
\(x=\log_{2}t\)
\(y=\log_{5}t={\large \frac{\log_{2}t}{\log_{2}5}}\)
\(z=\log_{10}t={\large \frac{\log_{2}t}{\log_{2}10}}\)
ここで、
\({\large \frac{1}{x}}+{\large \frac{1}{y}}\)
\(={\large \frac{1}{\log_{2}t}}+{\large \frac{\log_{2}5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}2+\log_{2}5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}2\times5}{\log_{2}t}}\)
\(={\large \frac{\log_{2}10}{\log_{2}t}}\)
\(={\large \frac{1}{z}}\)
したがって、
\({\large \frac{1}{x}}+{\large \frac{1}{y}}={\large \frac{1}{z}}\) [終]
p.187 練習問題B 15[証明]
\(a<b\) より、底が \(a\) の対数をとると、
\(\log_{a}a<\log_{a}b\)
\(~\Leftrightarrow~1<\log_{a}b\)
\(\log_{a}b>0\) より、これを両辺にかけると、
\(\log_{a}b<(\log_{a}b)^2\) …①
\(a<b\) より、底が \(a\) の対数をとると、
\(\log_{a}a<\log_{a}b\)
\(~\Leftrightarrow~1<\log_{a}b\)
\(\log_{a}b>0\) より、これを両辺にかけると、
\(\log_{a}b<(\log_{a}b)^2\) …①
次に、\(b<a^2\) より、底が \(a\) の対数をとると、
\(\log_{a}b<\log_{a}a^2\)
\(~\Leftrightarrow~\log_{a}b<2\)
\(\log_{a}b>0\) より、これを両辺にかけると、
\((\log_{a}b)^2<2\log_{a}b\)
よって、
\((\log_{a}b)^2<\log_{a}b^2\) …②
したがって、①と②より、
\(\log_{a}b<(\log_{a}b)^2<\log_{a}b^2\)
[終]
次のページ「5章 微分と積分」