文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第4章 三角関数
第5章 指数関数と対数関数
第6章 微分法と積分法
第1節 微分係数と導関数
p.169
練習4
\({\small (1)}~2\) \({\small (2)}~-4\)
練習4
\({\small (1)}~2\) \({\small (2)}~-4\)
p.170
練習5
\({\small (1)}~8\) \({\small (2)}~0\) \({\small (3)}~-4\)
練習5
\({\small (1)}~8\) \({\small (2)}~0\) \({\small (3)}~-4\)
p.171
練習6
\({\small (1)}~\)$$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{3(x+h)-3x}{h}$$$$~=\lim_{h\to0}\frac{3h}{h}$$$$~=3$$
\({\small (2)}~\) $$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{-(x+h)^2-(-x^2)}{h}$$$$~=\lim_{h\to0}\frac{-2xh-h^2}{h}$$$$~=\lim_{h\to0}(-2x-h)$$$$~=-2x$$
\({\small (3)}~\)$$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{4-4}{h}$$$$~=0$$→ 導関数
練習6
\({\small (1)}~\)$$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{3(x+h)-3x}{h}$$$$~=\lim_{h\to0}\frac{3h}{h}$$$$~=3$$
\({\small (2)}~\) $$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{-(x+h)^2-(-x^2)}{h}$$$$~=\lim_{h\to0}\frac{-2xh-h^2}{h}$$$$~=\lim_{h\to0}(-2x-h)$$$$~=-2x$$
\({\small (3)}~\)$$~~~~~f'(x)$$$$~=\lim_{h\to0}\frac{4-4}{h}$$$$~=0$$→ 導関数
p.171
練習7
\({\small (1)}~y’=4x^3\)
\({\small (2)}~y’=5x^4\)
練習7
\({\small (1)}~y’=4x^3\)
\({\small (2)}~y’=5x^4\)
p.173
練習8
\({\small (1)}~y’=8x+3\)
\({\small (2)}~y’=4x-5\)
\({\small (3)}~y’=-6x+1\)
\({\small (4)}~y’=-2x-1\)
\({\small (5)}~y’=3x^2+4x-3\)
\({\small (6)}~y’=-6x^2-2x+6\)
\({\small (7)}~y’=4x^2+{\large \frac{3}{2}}x-{\large \frac{1}{2}}\)
\({\small (8)}~y’=-x^2-{\large \frac{3}{2}}\)
練習8
\({\small (1)}~y’=8x+3\)
\({\small (2)}~y’=4x-5\)
\({\small (3)}~y’=-6x+1\)
\({\small (4)}~y’=-2x-1\)
\({\small (5)}~y’=3x^2+4x-3\)
\({\small (6)}~y’=-6x^2-2x+6\)
\({\small (7)}~y’=4x^2+{\large \frac{3}{2}}x-{\large \frac{1}{2}}\)
\({\small (8)}~y’=-x^2-{\large \frac{3}{2}}\)
p.174
練習9
\({\small (1)}~y’=2x+5\)
\({\small (2)}~y’=6x-12\)
\({\small (3)}~y’=3x^2-4\)
\({\small (4)}~y’=6x^2-8x-6\)
→ 微分の計算
練習9
\({\small (1)}~y’=2x+5\)
\({\small (2)}~y’=6x-12\)
\({\small (3)}~y’=3x^2-4\)
\({\small (4)}~y’=6x^2-8x-6\)
→ 微分の計算
p.174
練習10
\({\small (1)}~0\) \({\small (2)}~0\) \({\small (3)}~24\)
練習10
\({\small (1)}~0\) \({\small (2)}~0\) \({\small (3)}~24\)
p.175
練習11
\({\small (1)}~s’=6t-4\)
\({\small (2)}~f'(t)=3at^2+2bt\)
練習11
\({\small (1)}~s’=6t-4\)
\({\small (2)}~f'(t)=3at^2+2bt\)
p.175
練習12
\({\large \frac{dV}{dr}}=4\pi r^2~,~{\large \frac{dS}{dr}}=8\pi r\)
練習12
\({\large \frac{dV}{dr}}=4\pi r^2~,~{\large \frac{dS}{dr}}=8\pi r\)
補充問題
p.178
1
\({\small (1)}~-2\) \({\small (2)}~4a\)
1
\({\small (1)}~-2\) \({\small (2)}~4a\)
p.178
3
\(y=2~,~y={\large \frac{27}{4}}x-{\large \frac{19}{4}}\)
3
\(y=2~,~y={\large \frac{27}{4}}x-{\large \frac{19}{4}}\)
第2節 関数の値の変化
p.181
練習15
\({\small (1)}~\)
\(x≦0\) で増加
\(0≦x≦4\) で減少
\(4≦x\) で増加
\({\small (2)}~\)
\(x≦-2\) で減少
\(-2≦x≦1\) で増加
\(1≦x\) で減少
\({\small (3)}~\)常に減少
\({\small (4)}~\)常に増加
練習15
\({\small (1)}~\)
\(x≦0\) で増加
\(0≦x≦4\) で減少
\(4≦x\) で増加
\({\small (2)}~\)
\(x≦-2\) で減少
\(-2≦x≦1\) で増加
\(1≦x\) で減少
\({\small (3)}~\)常に減少
\({\small (4)}~\)常に増加
p.182
練習16
\({\small (1)}~\)

\(x=1\) で極大値 \(4\)
\(x=3\) で極小値 \(0\)
\({\small (2)}~\)

\(x=2\) で極大値 \(5\)
\(x=0\) で極小値 \(1\)
\({\small (3)}~\)

\(x=-2\) で極大値 \(8\)
\(x=0\) で極小値 \(0\)
\({\small (4)}~\)

\(x={\large \frac{2}{3}}\) で極大値 \({\large \frac{4}{27}}\)
\(x=0\) で極小値 \(0\)
→ 3次関数のグラフと増減表
練習16
\({\small (1)}~\)
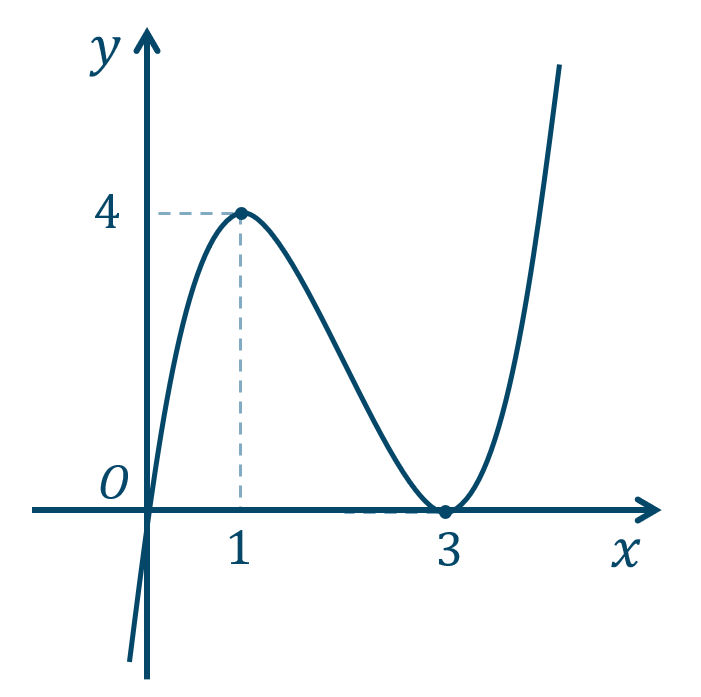
\(x=1\) で極大値 \(4\)
\(x=3\) で極小値 \(0\)
\({\small (2)}~\)
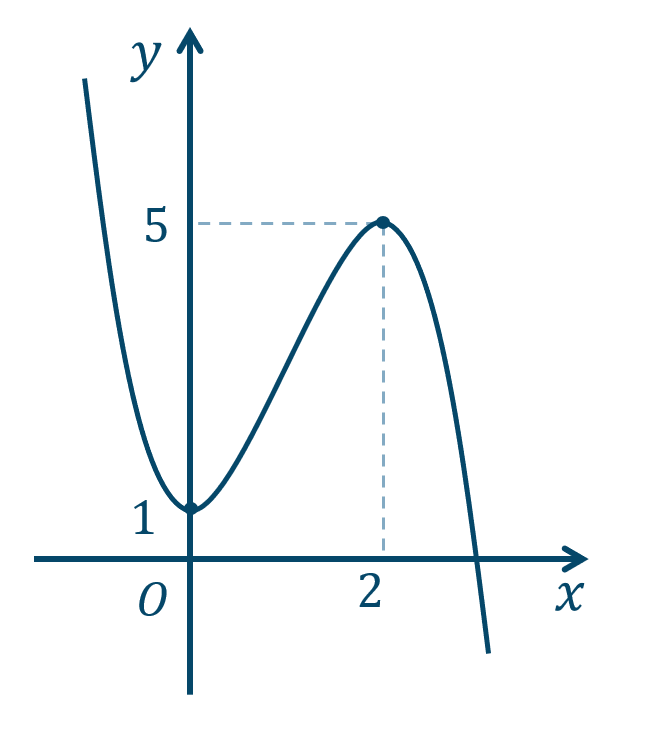
\(x=2\) で極大値 \(5\)
\(x=0\) で極小値 \(1\)
\({\small (3)}~\)
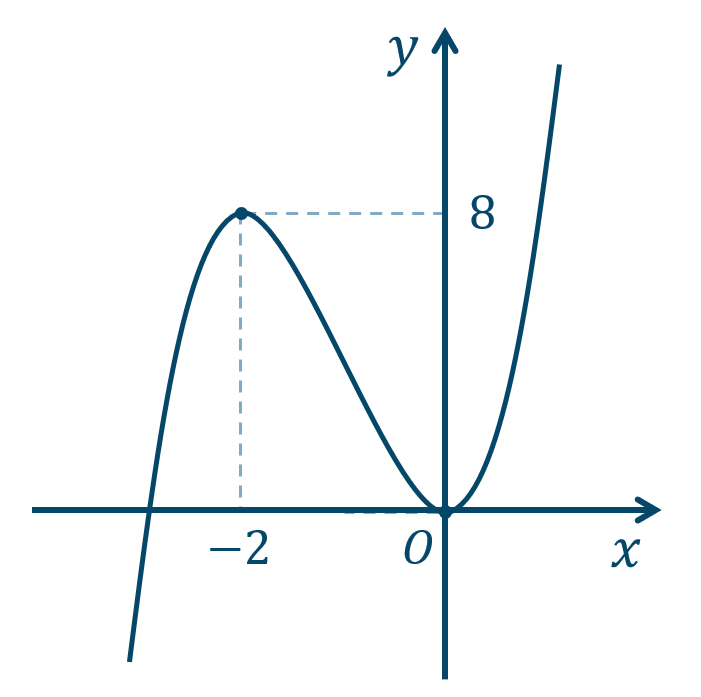
\(x=-2\) で極大値 \(8\)
\(x=0\) で極小値 \(0\)
\({\small (4)}~\)
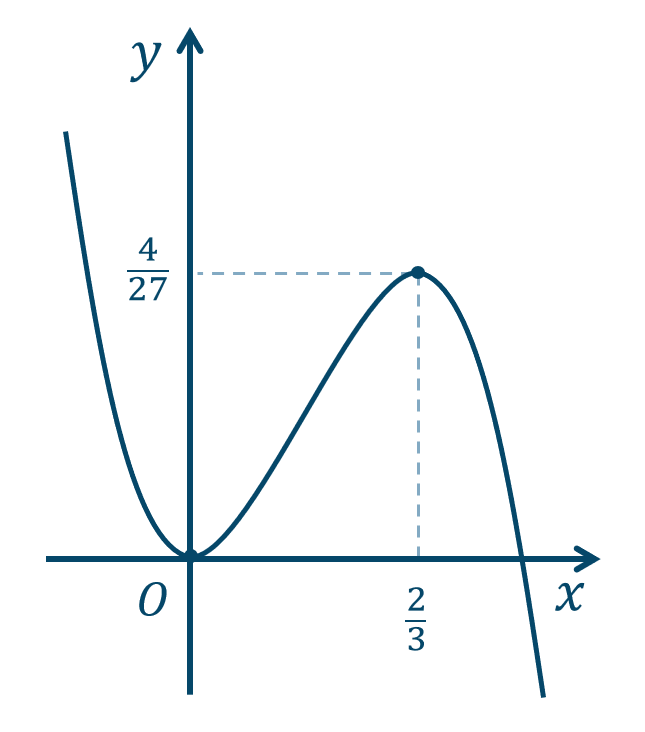
\(x={\large \frac{2}{3}}\) で極大値 \({\large \frac{4}{27}}\)
\(x=0\) で極小値 \(0\)
→ 3次関数のグラフと増減表
p.184
研究1
\({\small (1)}~y’=4x^3-1\)
\({\small (2)}~y’=-8x^3-3x^2+3\)
研究1
\({\small (1)}~y’=4x^3-1\)
\({\small (2)}~y’=-8x^3-3x^2+3\)
p.184
研究2
\({\small (1)}~\)

\(x=-2\) で極小値 \(-27\)
\(x=0\) で極大値 \(5\)
\(x=1\) で極小値 \(0\)
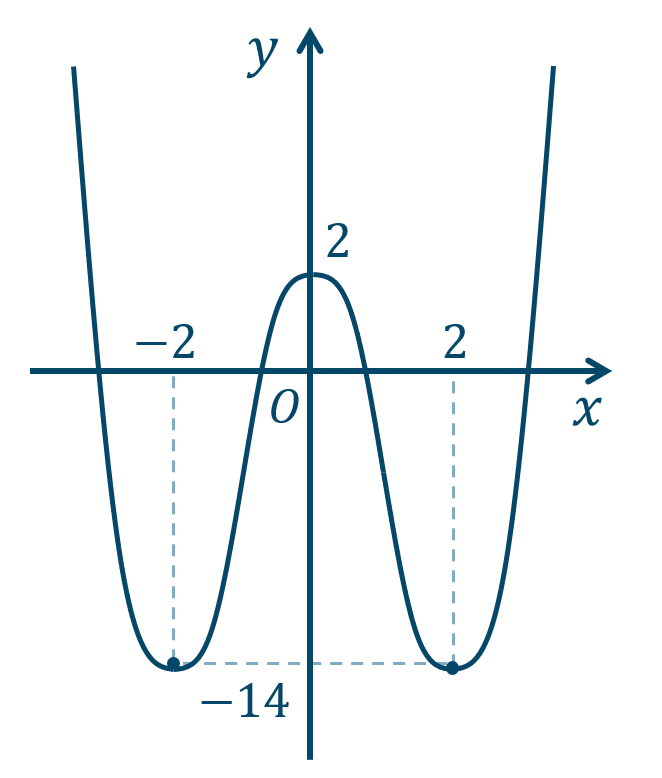
\({\small (2)}~\)

\(x=0\) で極大値 \(2\)
\(x=\pm2\) で極小値 \(-14\)
→ 4次関数のグラフと増減表
研究2
\({\small (1)}~\)
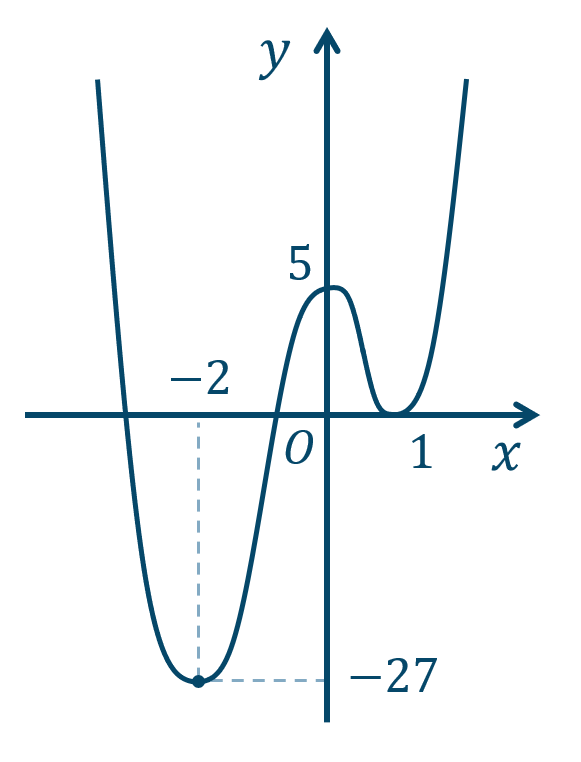
\(x=-2\) で極小値 \(-27\)
\(x=0\) で極大値 \(5\)
\(x=1\) で極小値 \(0\)
\({\small (2)}~\)
\(x=0\) で極大値 \(2\)
\(x=\pm2\) で極小値 \(-14\)
→ 4次関数のグラフと増減表
p.185
練習18
\({\small (1)}~\)
\(x=2\) で最大値 \(20\)
\(x=-3~,~0\) で最小値 \(0\)
\({\small (2)}~\)
\(x=-2~,~1\) で最大値 \(3\)
\(x=-1~,~2\) で最小値 \(-1\)
\({\small (3)}~\)
\(x=-1\) で最大値 \(8\)
\(x=2\) で最小値 \(-46\)
→ 3次関数の最大値・最小値
練習18
\({\small (1)}~\)
\(x=2\) で最大値 \(20\)
\(x=-3~,~0\) で最小値 \(0\)
\({\small (2)}~\)
\(x=-2~,~1\) で最大値 \(3\)
\(x=-1~,~2\) で最小値 \(-1\)
\({\small (3)}~\)
\(x=-1\) で最大値 \(8\)
\(x=2\) で最小値 \(-46\)
→ 3次関数の最大値・最小値
p.186
練習19
\(2\) ㎝
練習19
\(2\) ㎝
p.188
練習21
[証明]
\(f(x)=(x^3+3x^2+5)-9x\) とすると、
\(f'(x)=3x^2+6x-9\)
\(=3(x+3)(x-1)\)
よって、\(x≧0\) での増減表は
練習21
[証明]
\(f(x)=(x^3+3x^2+5)-9x\) とすると、
\(f'(x)=3x^2+6x-9\)
\(=3(x+3)(x-1)\)
よって、\(x≧0\) での増減表は
| \(x\) | \(0\) | \(\cdots\) | \(1\) | \(\cdots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) | |
| \(f(x)\) | \(5\) | ↘︎ | \(0\) | ↗︎ |
よって、\(x≧0\) で最小値が \(0\) であるので、
\(f(x)≧0\)
したがって、\(x≧0\) のとき
\(x^3+3x^2+5≧9x\)
また、等号が成り立つときは \(x=1\) のとき [終]
→ 3次不等式の証明
補充問題
p.189
4
\({\small (1)}~\)
\(x=-\sqrt{2}\) で極大値 \(2+4\sqrt{2}\)
\(x=\sqrt{2}\) で極小値 \(2-4\sqrt{2}\)
\({\small (2)}~\)極値なし
4
\({\small (1)}~\)
\(x=-\sqrt{2}\) で極大値 \(2+4\sqrt{2}\)
\(x=\sqrt{2}\) で極小値 \(2-4\sqrt{2}\)
\({\small (2)}~\)極値なし
p.189
5
\(a=-3~,~b=-9\)
\(x=-1\) で極大値 \(6\)
\(x=3\) で極小値 \(-26\)
5
\(a=-3~,~b=-9\)
\(x=-1\) で極大値 \(6\)
\(x=3\) で極小値 \(-26\)
p.189
6
\({\small (1)}~\)
\(V=\pi x^2(18-2x)~~~(0<x<9)\)
\({\small (2)}~6\) ㎝
6
\({\small (1)}~\)
\(V=\pi x^2(18-2x)~~~(0<x<9)\)
\({\small (2)}~6\) ㎝
第3節 積分法
p.190
練習22
②、④
練習22
②、④
p.191
練習23
[証明]
\(n\) が \(0\) または正の整数のとき、
\(F(x)={\large \frac{1}{n+1}}x^{n+1}\)
とすると、
\(F'(x)=(n+1)\cdot{\large \frac{1}{n+1}}x^{n}=x^n\)
よって、\(x^n\) の不定積分の1つは \(F(x)\) である
したがって、
\(\int x^n dx={\large \frac{1}{n+1}}x^{n+1}+C\)
[終]
また、\(C\) を積分定数として
\(\int x^3 dx={\large \frac{1}{4}}x^4+C\)
練習23
[証明]
\(n\) が \(0\) または正の整数のとき、
\(F(x)={\large \frac{1}{n+1}}x^{n+1}\)
とすると、
\(F'(x)=(n+1)\cdot{\large \frac{1}{n+1}}x^{n}=x^n\)
よって、\(x^n\) の不定積分の1つは \(F(x)\) である
したがって、
\(\int x^n dx={\large \frac{1}{n+1}}x^{n+1}+C\)
[終]
また、\(C\) を積分定数として
\(\int x^3 dx={\large \frac{1}{4}}x^4+C\)
p.192
練習24
\(C\) を積分定数として、
\({\small (1)}~2x^3+C\)
\({\small (2)}~{\large \frac{1}{3}}x^3+{\large \frac{1}{2}}x^2-x+C\)
\({\small (3)}~x^3-x^2+5x+C\)
\({\small (4)}~-{\large \frac{2}{3}}x^3-{\large \frac{1}{2}}x^2+7x+C\)
練習24
\(C\) を積分定数として、
\({\small (1)}~2x^3+C\)
\({\small (2)}~{\large \frac{1}{3}}x^3+{\large \frac{1}{2}}x^2-x+C\)
\({\small (3)}~x^3-x^2+5x+C\)
\({\small (4)}~-{\large \frac{2}{3}}x^3-{\large \frac{1}{2}}x^2+7x+C\)
p.193
練習25
\(C\) を積分定数として、
\({\small (1)}~{\large \frac{2}{3}}t^3-{\large \frac{3}{2}}t^2-4t+C\)
\({\small (2)}~-2u^3+{\large \frac{9}{2}}u^2-3u+C\)
→ 不定積分
練習25
\(C\) を積分定数として、
\({\small (1)}~{\large \frac{2}{3}}t^3-{\large \frac{3}{2}}t^2-4t+C\)
\({\small (2)}~-2u^3+{\large \frac{9}{2}}u^2-3u+C\)
→ 不定積分
p.195
練習27
\({\small (1)}~4\) \({\small (2)}~3\) \({\small (3)}~-6\)
練習27
\({\small (1)}~4\) \({\small (2)}~3\) \({\small (3)}~-6\)
p.195
練習28
\({\small (1)}~{\large \frac{2}{3}}\) \({\small (2)}~-{\large \frac{1}{6}}\)
練習28
\({\small (1)}~{\large \frac{2}{3}}\) \({\small (2)}~-{\large \frac{1}{6}}\)
p.196
練習29
\({\small (1)}~-{\large \frac{9}{2}}\) \({\small (2)}~-{\large \frac{68}{3}}\)
練習29
\({\small (1)}~-{\large \frac{9}{2}}\) \({\small (2)}~-{\large \frac{68}{3}}\)
p.196
練習30
\(0\)
練習30
\(0\)
p.201
練習34
\({\small (1)}~{\large \frac{26}{3}}\) \({\small (2)}~9\)
練習34
\({\small (1)}~{\large \frac{26}{3}}\) \({\small (2)}~9\)
p.202
練習35
\({\small (1)}~{\large \frac{4}{3}}\) \({\small (2)}~{\large \frac{4}{3}}\)
→ 定積分と面積①(x軸と囲まれた面積)
練習35
\({\small (1)}~{\large \frac{4}{3}}\) \({\small (2)}~{\large \frac{4}{3}}\)
→ 定積分と面積①(x軸と囲まれた面積)
p.204
練習36
\({\large \frac{11}{3}}\)
練習36
\({\large \frac{11}{3}}\)
p.204
練習37
\({\small (1)}~{\large \frac{9}{2}}\) \({\small (2)}~{\large \frac{32}{3}}\)
→ 定積分と面積②(2つの関数で囲まれた面積)
練習37
\({\small (1)}~{\large \frac{9}{2}}\) \({\small (2)}~{\large \frac{32}{3}}\)
→ 定積分と面積②(2つの関数で囲まれた面積)
p.206
研究1
\({\small (1)}~x^4+2x^3+3x+C\)
\({\small (2)}~-{\large \frac{3}{4}}\)
研究1
\({\small (1)}~x^4+2x^3+3x+C\)
\({\small (2)}~-{\large \frac{3}{4}}\)
p.206
研究2
\({\large \frac{37}{12}}\)
研究2
\({\large \frac{37}{12}}\)
補充問題
p.207
8
\({\small (1)}~8\) \({\small (2)}~{\large \frac{15}{2}}\)
8
\({\small (1)}~8\) \({\small (2)}~{\large \frac{15}{2}}\)
p.207
9
\({\small (1)}~9\) \({\small (2)}~{\large \frac{16}{3}}\)
9
\({\small (1)}~9\) \({\small (2)}~{\large \frac{16}{3}}\)
章末問題 微分法と積分法
章末問題A
p.208
1
\({\small (1)}~y’=-6x^2-2x+2\)
\({\small (2)}~y’=3x^2\)
1
\({\small (1)}~y’=-6x^2-2x+2\)
\({\small (2)}~y’=3x^2\)
p.208
2
\({\small (1)}~y=3x-18\)
\({\small (2)}~-{\large \frac{1}{3}}\)
2
\({\small (1)}~y=3x-18\)
\({\small (2)}~-{\large \frac{1}{3}}\)
p.208
3
\({\small (1)}~x=0\) で極大値 \(0\)
\({\small (2)}~\)極大値なし
\({\small (3)}~x={\large \frac{2}{3}}a\) で極大値 \(-{\large \frac{4}{27}}a^3\)
3
\({\small (1)}~x=0\) で極大値 \(0\)
\({\small (2)}~\)極大値なし
\({\small (3)}~x={\large \frac{2}{3}}a\) で極大値 \(-{\large \frac{4}{27}}a^3\)
p.208
4
\(a=1~,~b=-6~,~c=9~,~d=1\)
4
\(a=1~,~b=-6~,~c=9~,~d=1\)
p.208
5
\(0<a<32\)
5
\(0<a<32\)
p.208
6
\({\small (1)}~{\large \frac{172}{3}}\) \({\small (2)}~-{\large \frac{8\sqrt{2}}{3}}\)
6
\({\small (1)}~{\large \frac{172}{3}}\) \({\small (2)}~-{\large \frac{8\sqrt{2}}{3}}\)
p.208
7
\(x=1\) で極大値 \(0\)
7
\(x=1\) で極大値 \(0\)
p.208
8
\({\small (1)}~{\large \frac{49}{3}}\) \({\small (2)}~{\large \frac{39}{2}}\)
→ 定積分と面積③(区間付きの面積)
8
\({\small (1)}~{\large \frac{49}{3}}\) \({\small (2)}~{\large \frac{39}{2}}\)
→ 定積分と面積③(区間付きの面積)
章末問題B
p.209
9
\(k≧3\)
9
\(k≧3\)
p.209
10
\(k=32\)
10
\(k=32\)
p.209
11
\(V_1:V_2=8:27\)
11
\(V_1:V_2=8:27\)
p.209
12
[証明]
\(a\neq0\) として1次関数を
\(f(x)=ax+b\)
とすると、$$~~~~~~\int_{0}^{1}(ax+b)dx$$$$~=\left[ \frac{a}{2}x^2+bx \right]_{0}^{1}$$$$~=\frac{a}{2}+b$$次に、$$~~~~~~\int_{0}^{1}(ax+b)^2dx$$$$~=\int_{0}^{1}(a^2x^2+2abx+b^2)dx$$$$~=\left[ \frac{a^2}{3}x^3+abx^2+b^2x \right]_{0}^{1}$$$$~=\frac{a^2}{3}+ab+b^2$$よって、
(右辺)−(左辺)$$~=\left(\frac{a^2}{3}+ab+b^2\right)-\left(\frac{a}{2}+b\right)^2$$$$~=\frac{a^2}{12}>0$$したがって、$$~\left\{\int_{0}^{1}f(x)dx\right\}^2<\int_{0}^{1}\left\{f(x)\right\}^2dx$$[終]
12
[証明]
\(a\neq0\) として1次関数を
\(f(x)=ax+b\)
とすると、$$~~~~~~\int_{0}^{1}(ax+b)dx$$$$~=\left[ \frac{a}{2}x^2+bx \right]_{0}^{1}$$$$~=\frac{a}{2}+b$$次に、$$~~~~~~\int_{0}^{1}(ax+b)^2dx$$$$~=\int_{0}^{1}(a^2x^2+2abx+b^2)dx$$$$~=\left[ \frac{a^2}{3}x^3+abx^2+b^2x \right]_{0}^{1}$$$$~=\frac{a^2}{3}+ab+b^2$$よって、
(右辺)−(左辺)$$~=\left(\frac{a^2}{3}+ab+b^2\right)-\left(\frac{a}{2}+b\right)^2$$$$~=\frac{a^2}{12}>0$$したがって、$$~\left\{\int_{0}^{1}f(x)dx\right\}^2<\int_{0}^{1}\left\{f(x)\right\}^2dx$$[終]
p.209
14
\(a=2~,~-2\)
14
\(a=2~,~-2\)
p.209
15
\({\large \frac{16}{3}}\)
15
\({\large \frac{16}{3}}\)


