数研出版：改訂版高等学校数学Ⅱ

p.149
練習1
\({\small (1)}~1\)　\({\small (2)}~1\)　\({\small (3)}~{\large \frac{1}{3}}\)　\({\small (4)}~{\large \frac{1}{100}}\)　\({\small (5)}~-{\large \frac{1}{8}}\)

p.149
練習2
\({\small (1)}~a^3\)　\({\small (2)}~{\large \frac{1}{a^5}}\)　\({\small (3)}~a^4\)　\({\small (4)}~{\large \frac{b^3}{a^6}}\)
→ 指数法則の基本

p.150
練習3
\({\small (1)}~1\)　\({\small (2)}~3\)　\({\small (3)}~{\large \frac{1}{2}}\)

p.151
練習4
\({\small (1)}~3\)　\({\small (2)}~2\)　\({\small (3)}~\sqrt[\large 3]{25}\)
\({\small (4)}~\sqrt[\large 12]{12}\)　\({\small (5)}~\sqrt{2}\)
→ 累乗根

p.152
練習5
\({\small (1)}~3\)　\({\small (2)}~9\)　\({\small (3)}~{\large \frac{1}{25}}\)
→ 指数法則の拡張

p.153
練習6
\({\small (1)}~4\)　\({\small (2)}~1\)　\({\small (3)}~\sqrt[\large 8]{5}\)　\({\small (4)}~2\)
→ 指数法則を用いた計算

p.154
練習7
\(0.35~,~0.5~,~1~,~1.41\)

p.155
練習8

→ 指数関数のグラフ

p.156
練習9
\({\small (1)}~\sqrt[\large 5]{8}<\sqrt[\large 3]{4}<\sqrt[\large 4]{8}\)
\({\small (2)}~0.2^3<1<0.2^{-1}\)
→ 指数の大小比較

p.157
練習10
\({\small (1)}~x={\large \frac{3}{2}}\)　\({\small (2)}~x=-{\large \frac{4}{3}}\)
\({\small (3)}~x={\large \frac{1}{2}}\)
→ 指数方程式

p.157
練習11
\({\small (1)}~x<4\)
\({\small (2)}~x≦5\)
\({\small (3)}~x>{\large \frac{4}{5}}\)
→ 指数不等式

p.158
練習12
\({\small (1)}~x=0\)
\({\small (2)}~x=0~,~1\)
→ 指数関数を含む２次方程式

p.158
練習13
\({\small (1)}~x>1\)
\({\small (2)}~x≦2\)
→ 指数関数を含む２次不等式

p.159
1
\(-6\)

p.158
2
\({\small (1)}~3\sqrt[\large 3]{2}\)　\({\small (2)}~\sqrt[\large 4]{3}\)
\({\small (3)}~\sqrt{3}-\sqrt{2}\)　\({\small (4)}~{\large \frac{3}{2}}\)

p.158
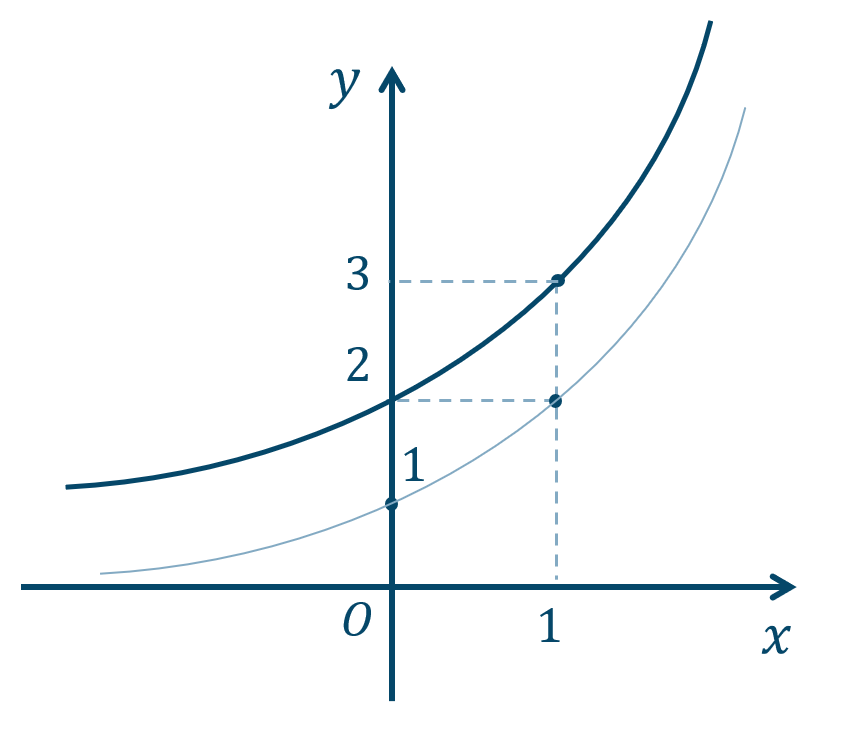
3
\({\small (1)}~\)

\({\small (2)}~\)

p.158
4
\({\small (1)}~x={\large \frac{5}{3}}\)　\({\small (2)}~x={\large \frac{2}{3}}\)
\({\small (3)}~x>{\large \frac{5}{2}}\)　\({\small (4)}~x≦{\large \frac{1}{2}}\)

p.158
5
\({\small (1)}~x=3\)　\({\small (2)}~x<1\)

p.158
6
ア:\(0\)　イ:\(4\)　ウ:\(1\)　エ:\(2\)　オ:\(1\)
カ:\(0\)　キ:\(2\)
→ 指数関数の最大値・最小値

p.160
練習14
\({\small (1)}~4\)　\({\small (2)}~2\)　\({\small (3)}~-3\)

p.161
練習15
\({\small (1)}~\log_{3}9=2\)
\({\small (2)}~\log_{5}{\large \frac{1}{25}}=-2\)
\({\small (3)}~\log_{{\Large \frac{1}{2}}}{\large \frac{1}{8}}=3\)
→ 指数と対数

p.161
練習16
\(3\)

p.161
練習17
\({\small (1)}~5\)　\({\small (2)}~2\)
\({\small (3)}~-3\)　\({\small (4)}~4\)
\({\small (5)}~-1\)　\({\small (6)}~-1\)
\({\small (7)}~{\large \frac{1}{3}}\)　\({\small (8)}~2\)
→ 対数の値

p.162
練習18
\({\small [2]}~\)
\(\log_{a}M=p~,~\log_{a}N=q\) とすると、
　\(M=a^p~,~N=a^q\)
\(N\neq0\) より、
　\({\large \frac{M}{N}}={\large \frac{a^p}{a^q}}=a^{p-q}\)
対数の定義より、
　\(\log_{a}{\large \frac{M}{N}}=p-q\)
したがって、
　\(\log_{a}{\large \frac{M}{N}}=\log_{a}M-\log_{a}N\) [終]
\({\small [3]}~\)
\(\log_{a}M=p\) とすると、\(M=a^p\)
両辺を \(k\) 乗すると、
　\(M^k=(a^p)^k=a^{pk}\)
ここで、\(\log_{a}\) を取ると
　\(\log_{a}M^k=\log_{a}a^{pk}=pk\)
したがって、\(p\) を元に戻すと、
　\(\log_{a}M^k=k\log_{a}M\) [終]

p.163
練習19
\({\small (1)}~2\)　\({\small (2)}~-2\)
\({\small (3)}~2\)　\({\small (4)}~{\large \frac{1}{3}}\)
→ 対数の計算

p.163
練習20
\({\small (1)}~{\large \frac{3}{2}}\)　\({\small (2)}~{\large \frac{1}{2}}\)　\({\small (3)}~3\)
→ 底の変換公式

p.165
練習21
\({\small (1)}~\)

\({\small (2)}~\)

→ 対数関数のグラフ

p.166
練習22
\({\small (1)}~2\log_{4}5<3\log_{4}3\)
\({\small (2)}~\log_{{\large \frac{1}{4}}}3<{\large \frac{1}{2}}\log_{{\large \frac{1}{4}}}8\)
\({\small (3)}~\log_{2}3<2\)
→ 対数の大小比較

p.166
練習23
\({\small (1)}~x=16\)　\({\small (2)}~x={\large \frac{1}{4}}\)
\({\small (3)}~0<x≦16\)　\({\small (4)}~x>{\large \frac{1}{4}}\)
\({\small (5)}~x>9\)　\({\small (6)}~0<x≦0.25\)

p.166
練習24
\({\small (1)}~x=8\)　\({\small (2)}~x=3\)
→ 対数方程式

p.167
練習25
\({\small (1)}~0<x≦1\)
\({\small (2)}~0<x<2\)
→ 対数不等式

p.168
練習26
\(x=16\) で最大値 \(8\)
\(x=2\) で最小値 \(-1\)
→ 対数含む関数の最大値・最小値

p.169
練習27
\({\small (1)}~3.5378\)
\({\small (2)}~4.9638\)
\({\small (3)}~-3.2090\)

p.170
練習28
\(31\) 桁
→ 常用対数（桁数問題・小数第何位）

p.171
練習29
\(n=15~,~16\)

p.171
練習30
小数第 \(7\) 位
→ 常用対数（桁数問題・小数第何位）

p.172
7
\({\small (1)}~b-3a\)　\({\small (2)}~{\large \frac{1}{3}}(a+b)\)
\({\small (3)}~{\large \frac{b}{a}}\)　\({\small (4)}~1-a+b\)

p.172
8
[証明]底の変換公式より、
　(左辺)$$~=\log_{a}b\cdot\frac{\log_{a}c}{\log_{a}b}\cdot\frac{\log_{a}a}{\log_{a}c}$$$$~=\log_{a}a=1$$したがって、
　\(\log_{a}b\cdot\log_{b}c\cdot\log_{c}a=1\)
[終]

p.172
9

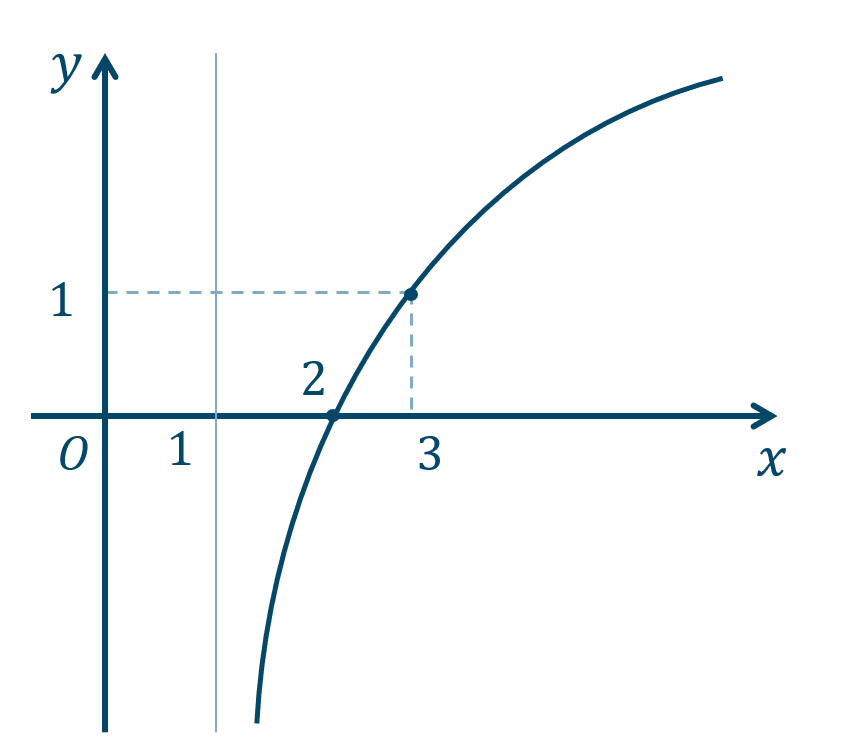
p.172
10
\({\small (1)}~x=2~,~-4\)
\({\small (2)}~x=1\)
\({\small (3)}~1<x<{\large \frac{5}{4}}\)
\({\small (4)}~2<x<3\)

p.172
11
\(n=14\)

p.172
12
小数第 \(7\) 位

p.172
13
ア:\(0\)　イ:\(3\)　ウ:\(2\)　エ:\(2\)　オ:\(2\)
カ:\(4\)　キ:\(2\)
→ 対数を含む２次式

p.173
1
\({\small (1)}~8\)　\({\small (2)}~\sqrt[\large 4]{3}\)

p.173
2
\({\small (1)}~-1≦x≦3\)
\({\small (2)}~-2≦x≦0\)

p.173
3
\({\small (1)}~x=-{\large \frac{1}{3}}\)
\({\small (2)}~x≦2\)
\({\small (3)}~x≦{\large \frac{2}{3}}\)

p.173
4
\({\small (1)}~0\)　\({\small (2)}~5\)　\({\small (3)}~0\)

p.173
5
\({\small (1)}~x=0~,~-3\)
\({\small (2)}~x=5\)
\({\small (3)}~1≦x<3\)
\({\small (4)}~x≧3\)

p.173
6
\(16\) 桁

p.173
7
\(n=6~,~7\)

p.173
8
\(9\) 時間後

p.174
9
\({\small (1)}~7\)　\({\small (2)}~47\)

p.174
10
\({\small (1)}~{\large \frac{1}{4}}≦y≦16\)
\({\small (2)}~-{\large \frac{3}{2}}≦y≦-{\large \frac{1}{2}}\)

p.174
11
\({\small (1)}~3\)　\({\small (2)}~2\)

p.174
12
\(x=3\) で最大値 \(2\)

p.174
13
[証明]
\(2^x=10^z\) より、
　\(z=\log_{10}2^x=x\log_{10}2\)
これより、
　\(x={\large \frac{z}{\log_{10}2}}\)
また、\(5^y=10^z\) より、
　\(z=\log_{10}5^y=y\log_{10}5\)
これより、
　\(y={\large \frac{z}{\log_{10}5}}\)
よって、
　(左辺)$$~=\frac{1}{x}+\frac{1}{y}$$$$~=\frac{\log_{10}2}{z}+\frac{\log_{10}5}{z}$$$$~=\frac{\log_{10}2\times5}{z}$$$$~=\frac{\log_{10}10}{z}$$$$~=\frac{1}{z}$$したがって、
　\({\large \frac{1}{x}}+{\large \frac{1}{y}}={\large \frac{1}{z}}\)
[終]

p.174
14
\(4<3^{\sqrt{2}}\)

p.174
15
\({\small (1)}~0.3181\)
\({\small (2)}~2.08\)

p.174
16
\(n=31\)