このページは、数研出版:高等学校数学C[709]
第2章 空間のベクトル
第2章 空間のベクトル

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
高等学校数学C 第1章 平面のベクトル
高等学校数学C 第2章 空間のベクトル
高等学校数学C 第3章 複素数平面
高等学校数学C 第4章 式と曲線
第2章 空間のベクトル
p.51 練習1 \({\small (1)}~(-1~,~3~,~2)\)
\({\small (2)}~(1~,~-3~,~2)\)
\({\small (3)}~(-1~,~-3~,~2)\)
\({\small (4)}~(-1~,~-3~,~-2)\)
解法のPoint|平面・軸・原点に対称な点の座標
\({\small (2)}~(1~,~-3~,~2)\)
\({\small (3)}~(-1~,~-3~,~2)\)
\({\small (4)}~(-1~,~-3~,~-2)\)
解法のPoint|平面・軸・原点に対称な点の座標
p.52 練習3 等しいベクトル \(\overrightarrow{\rm BF}~,~\overrightarrow{\rm CG}~,~\overrightarrow{\rm DH}\)
逆ベクトル \(\overrightarrow{\rm CB}~,~\overrightarrow{\rm GF}~,~\overrightarrow{\rm HE}\)
逆ベクトル \(\overrightarrow{\rm CB}~,~\overrightarrow{\rm GF}~,~\overrightarrow{\rm HE}\)
p.53 練習5 \({\small (1)}~\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\)
\({\small (2)}~-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
\({\small (3)}~\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\)
\({\small (4)}~\overrightarrow{a}-\overrightarrow{b}\)
解法のPoint|平行六面体とベクトルの加法・減法
\({\small (2)}~-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
\({\small (3)}~\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\)
\({\small (4)}~\overrightarrow{a}-\overrightarrow{b}\)
解法のPoint|平行六面体とベクトルの加法・減法
p.55 練習6 \(~~~x=6~,~y=-3~,~z=4\)
p.57 練習8 \({\small (1)}~(5~,~0~,~-2)\)
\({\small (2)}~(-3~,~6~,~-2)\)
\({\small (3)}~(14~,~-3~,~-4)\)
\({\small (4)}~(21~,~-27~,~6)\)
解法のPoint|空間ベクトルの成分計算
\({\small (2)}~(-3~,~6~,~-2)\)
\({\small (3)}~(14~,~-3~,~-4)\)
\({\small (4)}~(21~,~-27~,~6)\)
解法のPoint|空間ベクトルの成分計算
p.57 練習9 \({\small (1)}~(1~,~-2~,~1)~,~\sqrt{6}\)
\({\small (2)}~(-2~,~-4~,~4)~,~6\)
解法のPoint|空間の点をベクトルの成分で表す
\({\small (2)}~(-2~,~-4~,~4)~,~6\)
解法のPoint|空間の点をベクトルの成分で表す
p.61 練習13 \(~~~\overrightarrow{p}=\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\,}{4}\)
解法のPoint|空間の位置ベクトルと内分点・外分点・中点
解法のPoint|空間内の三角形の重心の位置ベクトル
解法のPoint|空間の位置ベクトルと内分点・外分点・中点
解法のPoint|空間内の三角形の重心の位置ベクトル
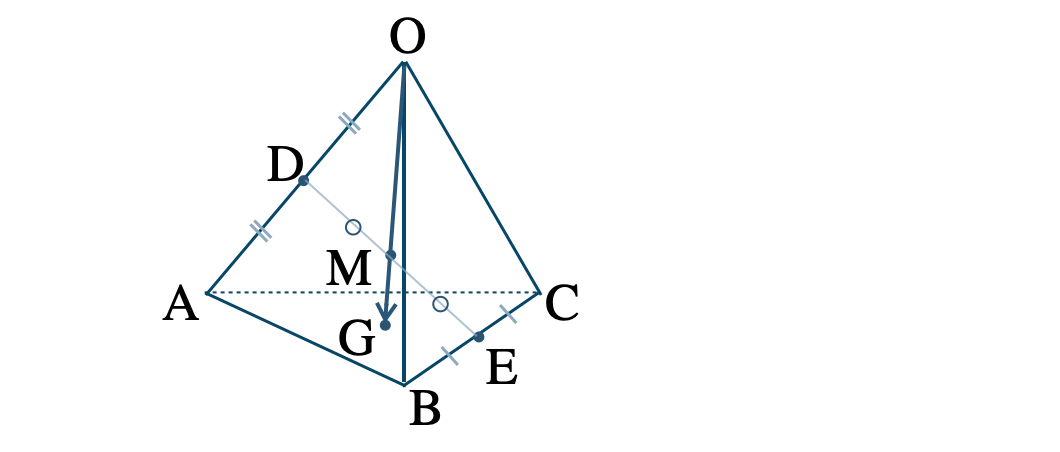
p.62 練習14 [証明]

\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\( {\rm D} \) は辺 \( {\rm OA} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\( {\rm E} \) は辺 \( {\rm BC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&\overrightarrow{\rm OB}+\overrightarrow{\rm BE}
\\[5pt]~~~&=&\overrightarrow{\rm OB}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\( {\rm M} \) は線分 \( {\rm DE} \) の中点より、\(\small [\,1\,]\)\(\small [\,2\,]\) から、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OD}+\overrightarrow{\rm OE}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
また、\( \triangle {\rm ABC} \) の重心が \( {\rm G} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small [\,3\,]\)\(\small [\,4\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}\cdot\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}\overrightarrow{\rm OM}\hspace{30pt}(\,∵~ {\small [\,3\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm OG}=\displaystyle \frac{\,4\,}{\,3\,}\overrightarrow{\rm OM} \) より、
3点 \( \rm O~,~\rm M~,~\rm G \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\( {\rm D} \) は辺 \( {\rm OA} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\( {\rm E} \) は辺 \( {\rm BC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&\overrightarrow{\rm OB}+\overrightarrow{\rm BE}
\\[5pt]~~~&=&\overrightarrow{\rm OB}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\( {\rm M} \) は線分 \( {\rm DE} \) の中点より、\(\small [\,1\,]\)\(\small [\,2\,]\) から、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OD}+\overrightarrow{\rm OE}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
また、\( \triangle {\rm ABC} \) の重心が \( {\rm G} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small [\,3\,]\)\(\small [\,4\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}\cdot\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}\overrightarrow{\rm OM}\hspace{30pt}(\,∵~ {\small [\,3\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm OG}=\displaystyle \frac{\,4\,}{\,3\,}\overrightarrow{\rm OM} \) より、
3点 \( \rm O~,~\rm M~,~\rm G \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
p.64 練習16 \(~~~\overrightarrow{\rm OP}=\displaystyle \frac{1}{\,3\,}\overrightarrow{a}+\displaystyle \frac{4}{\,9\,}\overrightarrow{b}+\displaystyle \frac{2}{\,9\,}\overrightarrow{c}\)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
p.66 練習17 [証明] \( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\overrightarrow{\rm AC}=\overrightarrow{y}~,~\overrightarrow{\rm AD}=\overrightarrow{z} \) とおくと、
正四面体の1辺の長さを \(a\) とすると、
\(|\overrightarrow{x}|=|\overrightarrow{y}|=|\overrightarrow{z}|=a\)
\(|{\rm BC}|=a\) より、
\(\begin{eqnarray}~~~|\overrightarrow{\rm BC}|^2&=&a^2\\[5pt]~~~|\overrightarrow{y}-\overrightarrow{x}|^2&=&a^2\\[5pt]~~~|\overrightarrow{x}|^2-2\overrightarrow{x}\cdot\overrightarrow{y}+|\overrightarrow{y}|^2&=&a^2\\[5pt]~~~a^2-2\overrightarrow{x}\cdot\overrightarrow{y}+a^2&=&a^2\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{y}&=&\displaystyle \frac{\,a^2\,}{\,2\,}\end{eqnarray}\)
同様に、\(|{\rm CD}|=|{\rm BD}|=a\) より、
\(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}=\displaystyle \frac{\,a^2\,}{\,2\,}\)
よって、
\(\overrightarrow{x}\cdot\overrightarrow{y}=\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}~ ~ ~ \cdots {\small [\,1\,]}\)
\(\triangle{\rm BCD}\) の重心 \({\rm G}\) の位置ベクトルは、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{\rm AB}+\overrightarrow{\rm AC}+\overrightarrow{\rm AD})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm AG} \) と \( \overrightarrow{\rm BC} \) の内積は、
正四面体より \(|\overrightarrow{x}|=|\overrightarrow{y}|\) かつ \({\small [\,1\,]}\) より \(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}\) なので、
\(\begin{eqnarray}\hspace{35pt}&=&\displaystyle \frac{\,1\,}{\,3\,}(0+0)\\[5pt]~~~&=&0\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AG}\neq 0~,~\overrightarrow{\rm BC}\neq 0~,~\overrightarrow{\rm AG}\cdot\overrightarrow{\rm BC}=0 \) より、\( \overrightarrow{\rm AG}\perp\overrightarrow{\rm BC} \) [終]
■ この問題の詳しい解説はこちら!
正四面体の1辺の長さを \(a\) とすると、
\(|\overrightarrow{x}|=|\overrightarrow{y}|=|\overrightarrow{z}|=a\)
\(|{\rm BC}|=a\) より、
\(\begin{eqnarray}~~~|\overrightarrow{\rm BC}|^2&=&a^2\\[5pt]~~~|\overrightarrow{y}-\overrightarrow{x}|^2&=&a^2\\[5pt]~~~|\overrightarrow{x}|^2-2\overrightarrow{x}\cdot\overrightarrow{y}+|\overrightarrow{y}|^2&=&a^2\\[5pt]~~~a^2-2\overrightarrow{x}\cdot\overrightarrow{y}+a^2&=&a^2\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{y}&=&\displaystyle \frac{\,a^2\,}{\,2\,}\end{eqnarray}\)
同様に、\(|{\rm CD}|=|{\rm BD}|=a\) より、
\(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}=\displaystyle \frac{\,a^2\,}{\,2\,}\)
よって、
\(\overrightarrow{x}\cdot\overrightarrow{y}=\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}~ ~ ~ \cdots {\small [\,1\,]}\)
\(\triangle{\rm BCD}\) の重心 \({\rm G}\) の位置ベクトルは、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{\rm AB}+\overrightarrow{\rm AC}+\overrightarrow{\rm AD})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm AG} \) と \( \overrightarrow{\rm BC} \) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}\cdot\overrightarrow{\rm BC}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})\cdot(\overrightarrow{\rm AC}-\overrightarrow{\rm AB})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})\cdot(\overrightarrow{y}-\overrightarrow{x})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}\cdot\overrightarrow{y}-|\overrightarrow{x}|^2+|\overrightarrow{y}|^2-\overrightarrow{x}\cdot\overrightarrow{y}+\overrightarrow{y}\cdot\overrightarrow{z}-\overrightarrow{z}\cdot\overrightarrow{x})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(-|\overrightarrow{x}|^2+|\overrightarrow{y}|^2+\overrightarrow{y}\cdot\overrightarrow{z}-\overrightarrow{z}\cdot\overrightarrow{x})\end{eqnarray}\)
正四面体より \(|\overrightarrow{x}|=|\overrightarrow{y}|\) かつ \({\small [\,1\,]}\) より \(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}\) なので、
\(\begin{eqnarray}\hspace{35pt}&=&\displaystyle \frac{\,1\,}{\,3\,}(0+0)\\[5pt]~~~&=&0\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AG}\neq 0~,~\overrightarrow{\rm BC}\neq 0~,~\overrightarrow{\rm AG}\cdot\overrightarrow{\rm BC}=0 \) より、\( \overrightarrow{\rm AG}\perp\overrightarrow{\rm BC} \) [終]
■ この問題の詳しい解説はこちら!
p.67 練習18 \({\small (1)}~3\sqrt{6}\)
解法のPoint|空間の2点間の距離
\({\small (2)}~\left(\displaystyle \frac{\,5\,}{2},0,-\displaystyle \frac{1}{\,2\,}\right)\)
\({\small (3)}~(3~,~-1~,~0)\)
\({\small (4)}~(7~,~-9~,~4)\)
解法のPoint|座標空間の2点の内分点・外分点・中点
解法のPoint|空間の2点間の距離
\({\small (2)}~\left(\displaystyle \frac{\,5\,}{2},0,-\displaystyle \frac{1}{\,2\,}\right)\)
\({\small (3)}~(3~,~-1~,~0)\)
\({\small (4)}~(7~,~-9~,~4)\)
解法のPoint|座標空間の2点の内分点・外分点・中点
p.69 練習21 \({\small (1)}~x^2+y^2+z^2=9\)
\({\small (2)}~(x-1)^2+(y-2)^2+(z+3)^2=16\)
解法のPoint|中心と半径が条件の球面の方程式
\({\small (3)}~x^2+(y-4)^2+(z-1)^2=20\)
解法のPoint|中心と通る点が条件の球面の方程式
\({\small (4)}~x^2+(y-3)^2+(z+1)^2=17\)
解法のPoint|直径の両端が条件の球面の方程式
\({\small (2)}~(x-1)^2+(y-2)^2+(z+3)^2=16\)
解法のPoint|中心と半径が条件の球面の方程式
\({\small (3)}~x^2+(y-4)^2+(z-1)^2=20\)
解法のPoint|中心と通る点が条件の球面の方程式
\({\small (4)}~x^2+(y-3)^2+(z+1)^2=17\)
解法のPoint|直径の両端が条件の球面の方程式
問題
p.72 問題 1 \( \overrightarrow{p}=\overrightarrow{a}-2\overrightarrow{b}-3\overrightarrow{c} \)
解法のPoint|成分計算とベクトルの表し方
解法のPoint|成分計算とベクトルの表し方
p.72 問題 3[証明]

\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm OB}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \triangle {\rm ABC} \) の重心が \( {\rm G} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
さらに、\( {\rm M} \) は辺 \( {\rm OC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OC}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DG}&=&\overrightarrow{\rm OG}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{a}-3\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,3\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DM}&=&\overrightarrow{\rm OM}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&-\overrightarrow{a}-\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,5\,]}
\end{eqnarray}\)
\(\small [\,4\,]\)\(\small [\,5\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DG}&=&\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\cdot\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm DM}\hspace{30pt}(\,∵~ {\small [\,5\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm DG}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm DM} \) より、
点 \( {\rm G} \) は線分 \( {\rm DM} \) 上にあり、\( {\rm DM} \) を \( 2:1 \) に内分する [終]
■ この問題の詳しい解説はこちら!
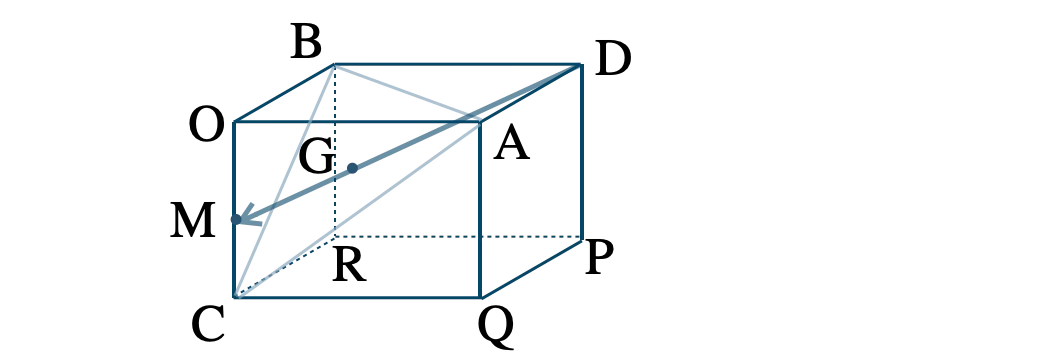
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm OB}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \triangle {\rm ABC} \) の重心が \( {\rm G} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
さらに、\( {\rm M} \) は辺 \( {\rm OC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OC}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DG}&=&\overrightarrow{\rm OG}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{a}-3\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,3\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DM}&=&\overrightarrow{\rm OM}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&-\overrightarrow{a}-\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,5\,]}
\end{eqnarray}\)
\(\small [\,4\,]\)\(\small [\,5\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DG}&=&\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\cdot\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm DM}\hspace{30pt}(\,∵~ {\small [\,5\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm DG}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm DM} \) より、
点 \( {\rm G} \) は線分 \( {\rm DM} \) 上にあり、\( {\rm DM} \) を \( 2:1 \) に内分する [終]
■ この問題の詳しい解説はこちら!
p.72 問題 5\({\small (1)}~\) \( {\rm AB}\perp{\rm OP} \)
\({\small (2)}~\) \( (0~,~2~,~1) \)
\({\small (1)}\) で予想した関係について、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}&=&0\cdot(-4)+2\cdot2+1\cdot(-4)
\\[3pt]~~~&=&0+4-4
\\[3pt]~~~&=&0\end{eqnarray}\)
よって、\( \overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}=0 \) より、直線 \(\rm AB\) と直線 \(\rm OP\) は垂直に交わる
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( (0~,~2~,~1) \)
\({\small (1)}\) で予想した関係について、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}&=&0\cdot(-4)+2\cdot2+1\cdot(-4)
\\[3pt]~~~&=&0+4-4
\\[3pt]~~~&=&0\end{eqnarray}\)
よって、\( \overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}=0 \) より、直線 \(\rm AB\) と直線 \(\rm OP\) は垂直に交わる
■ この問題の詳しい解説はこちら!
章末問題
p.73 章末問題A 1 \( s=\displaystyle \frac{\,1\,}{\,2\,}~,~t=\displaystyle \frac{\,1\,}{\,2\,} \)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
p.73 章末問題A 4\({\small (1)}~\) \( \overrightarrow{\rm OB}=(2~,~2~,~0)~,~\overrightarrow{\rm CF}=(2~,~0~,~2) \)
\({\small (2)}~\) \( 4 \) \({\small (3)}~\) \( 60^{\circ} \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( 4 \) \({\small (3)}~\) \( 60^{\circ} \)
■ この問題の詳しい解説はこちら!
p.73 章末問題A 5\({\small (1)}~\) \( \cos\alpha=-\displaystyle \frac{\,1\,}{\,2\,}~,~\cos\beta=\displaystyle \frac{\,\sqrt{2}\,}{\,2\,}~,~\cos\gamma=\displaystyle \frac{\,1\,}{\,2\,} \)
\({\small (2)}~\) \( \alpha=120^{\circ}~,~\beta=45^{\circ}~,~\gamma=60^{\circ} \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( \alpha=120^{\circ}~,~\beta=45^{\circ}~,~\gamma=60^{\circ} \)
■ この問題の詳しい解説はこちら!
p.73 章末問題A 6\({\small (1)}~\) \( (10~,~0~,~0) \)
解法のPoint|空間の2点から等距離にある点の座標
\({\small (2)}~\) \( \left(\,\displaystyle \frac{\,13\,}{\,3\,}~,~\displaystyle \frac{\,5\,}{\,3\,}~,~2\,\right) \)
解法のPoint|空間内の三角形の重心の位置ベクトル
解法のPoint|空間の2点から等距離にある点の座標
\({\small (2)}~\) \( \left(\,\displaystyle \frac{\,13\,}{\,3\,}~,~\displaystyle \frac{\,5\,}{\,3\,}~,~2\,\right) \)
解法のPoint|空間内の三角形の重心の位置ベクトル
p.74 章末問題B 10\({\small (1)}~\) \( 0 \) \({\small (2)}~\) \( 2|\,\overrightarrow{\rm BP}\,|+2|\,\overrightarrow{\rm HQ}\,| \)
\({\small (3)}~\) \( 8 \)
\({\small (3)}~\) \( 8 \)
p.74 章末問題B 11[証明] \( \overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}~,~\overrightarrow{\rm AD}=\overrightarrow{d} \) とおくと、
\({\rm AC}\perp{\rm BD}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}\cdot\overrightarrow{\rm BD}&=&0\\[5pt]~~~\overrightarrow{\rm AC}\cdot(\overrightarrow{\rm AD}-\overrightarrow{\rm AB})&=&0\\[5pt]~~~\overrightarrow{c}\cdot(\overrightarrow{d}-\overrightarrow{b})&=&0\\[5pt]~~~\overrightarrow{c}\cdot\overrightarrow{d}-\overrightarrow{b}\cdot\overrightarrow{c}&=&0\\[5pt]~~~\overrightarrow{c}\cdot\overrightarrow{d}&=&\overrightarrow{b}\cdot\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
ここで、
\(\begin{eqnarray}~~~{\rm AB}^2+{\rm CD}^2&=&|\overrightarrow{\rm AB}|^2+|\overrightarrow{\rm CD}|^2\\[5pt]~~~&=&|\overrightarrow{b}|^2+|\overrightarrow{d}-\overrightarrow{c}|^2\\[5pt]~~~&=&|\overrightarrow{b}|^2+|\overrightarrow{c}|^2-2\overrightarrow{c}\cdot\overrightarrow{d}+|\overrightarrow{d}|^2\end{eqnarray}\)
\({\small [\,1\,]}\) より、
\(\begin{eqnarray}\hspace{20pt}&=&|\overrightarrow{b}|^2+|\overrightarrow{c}|^2-2\overrightarrow{b}\cdot\overrightarrow{c}+|\overrightarrow{d}|^2\\[5pt]~~~&=&|\overrightarrow{d}|^2+|\overrightarrow{b}|^2-2\overrightarrow{b}\cdot\overrightarrow{c}+|\overrightarrow{c}|^2~ ~ ~ \cdots {\small [\,3\,]}\end{eqnarray}\)
\({\small [\,2\,]}\) と \({\small [\,3\,]}\) より、
\({\rm AD}^2+{\rm BC}^2={\rm AB}^2+{\rm CD}^2\) [終]
■ この問題の詳しい解説はこちら!
\({\rm AC}\perp{\rm BD}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}\cdot\overrightarrow{\rm BD}&=&0\\[5pt]~~~\overrightarrow{\rm AC}\cdot(\overrightarrow{\rm AD}-\overrightarrow{\rm AB})&=&0\\[5pt]~~~\overrightarrow{c}\cdot(\overrightarrow{d}-\overrightarrow{b})&=&0\\[5pt]~~~\overrightarrow{c}\cdot\overrightarrow{d}-\overrightarrow{b}\cdot\overrightarrow{c}&=&0\\[5pt]~~~\overrightarrow{c}\cdot\overrightarrow{d}&=&\overrightarrow{b}\cdot\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
ここで、
\(\begin{eqnarray}~~~{\rm AD}^2+{\rm BC}^2&=&|\overrightarrow{\rm AD}|^2+|\overrightarrow{\rm BC}|^2\\[5pt]~~~&=&|\overrightarrow{d}|^2+|\overrightarrow{c}-\overrightarrow{b}|^2\\[5pt]~~~&=&|\overrightarrow{d}|^2+|\overrightarrow{b}|^2-2\overrightarrow{b}\cdot\overrightarrow{c}+|\overrightarrow{c}|^2~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\(\begin{eqnarray}~~~{\rm AB}^2+{\rm CD}^2&=&|\overrightarrow{\rm AB}|^2+|\overrightarrow{\rm CD}|^2\\[5pt]~~~&=&|\overrightarrow{b}|^2+|\overrightarrow{d}-\overrightarrow{c}|^2\\[5pt]~~~&=&|\overrightarrow{b}|^2+|\overrightarrow{c}|^2-2\overrightarrow{c}\cdot\overrightarrow{d}+|\overrightarrow{d}|^2\end{eqnarray}\)
\({\small [\,1\,]}\) より、
\(\begin{eqnarray}\hspace{20pt}&=&|\overrightarrow{b}|^2+|\overrightarrow{c}|^2-2\overrightarrow{b}\cdot\overrightarrow{c}+|\overrightarrow{d}|^2\\[5pt]~~~&=&|\overrightarrow{d}|^2+|\overrightarrow{b}|^2-2\overrightarrow{b}\cdot\overrightarrow{c}+|\overrightarrow{c}|^2~ ~ ~ \cdots {\small [\,3\,]}\end{eqnarray}\)
\({\small [\,2\,]}\) と \({\small [\,3\,]}\) より、
\({\rm AD}^2+{\rm BC}^2={\rm AB}^2+{\rm CD}^2\) [終]
■ この問題の詳しい解説はこちら!
次のページ「第3章 複素数平面」


