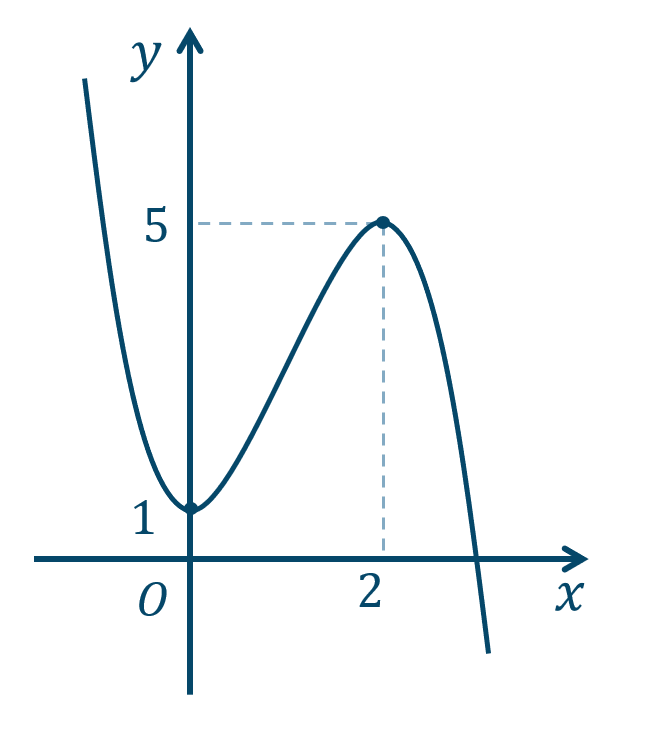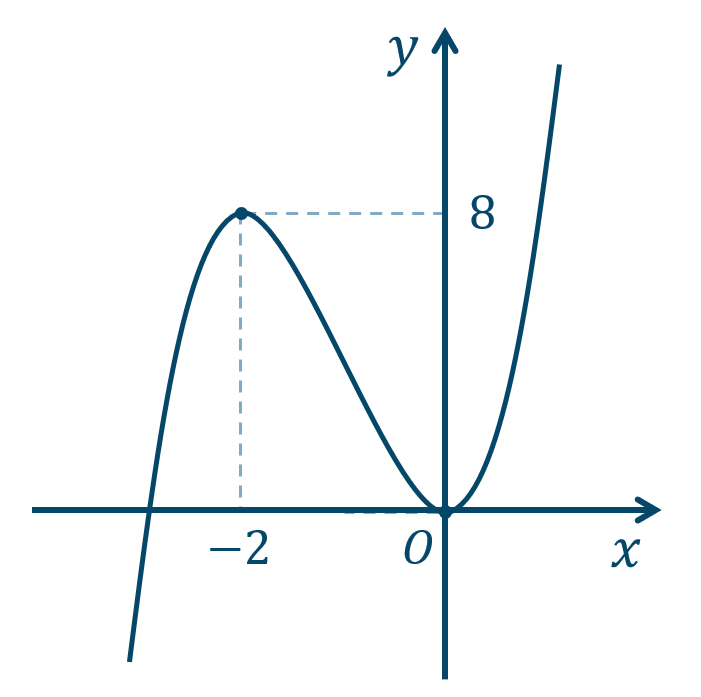【新課程】数研出版：新編数学Ⅱ[711]

p.179 練習1$${\small (1)}~2$$$${\small (2)}~-4-h$$→ 平均変化率

p.179 練習2$${\small (1)}~6$$$${\small (2)}~12$$→ 極限値

p.180 練習3$${\small (1)}~2$$$${\small (2)}~-12$$→ 微分係数

p.181 練習4$${\small (1)}~2$$$${\small (2)}~-4$$

p.182 練習5$${\small (1)}~8$$$${\small (2)}~0$$$${\small (3)}~-4$$

p.183 練習6\({\small (1)}~\)$$\begin{split}&f'(x)\\[2pt]~~=~&\lim_{h\to0}\frac{\,3(x+h)-3x\,}{h}\\[2pt]~~=~&\lim_{h\to0}\frac{\,3h\,}{h}\\[2pt]~~=~&3\end{split}$$
\({\small (2)}~\)$$\begin{split}&f'(x)\\[2pt]~~=~&\lim_{h\to0}\frac{\,-(x+h)^2-(-x^2)\,}{h}\\[2pt]~~=~&\lim_{h\to0}\frac{\,-2xh-h^2\,}{h}\\[2pt]~~=~&\lim_{h\to0}(-2x-h)\\[2pt]~~=~&-2x\end{split}$$
\({\small (3)}~\)$$\begin{split}&f'(x)\\[2pt]~~=~&\lim_{h\to0}\frac{\,4-4\,}{h}\\[2pt]~~=~&\lim_{h\to0}0\\[2pt]~~=~&0\end{split}$$→ 導関数

p.183 練習7$${\small (1)}~y’=4x^3$$$${\small (2)}~y’=5x^4$$

p.185 練習8$${\small (1)}~y’=8x+3$$$${\small (2)}~y’=4x-5$$$${\small (3)}~y’=-6x+1$$$${\small (4)}~y’=-2x-1$$$${\small (5)}~y’=3x^2+4x-3$$$${\small (6)}~y’=-6x^2-2x+6$$$${\small (7)}~y’=4x^2+{ \frac{\,3\,}{2}}x-{ \frac{1}{\,2\,}}$$$${\small (8)}~y’=-x^2-{ \frac{\,3\,}{2}}$$

p.186
練習9$${\small (1)}~y’=2x+5$$$${\small (2)}~y’=6x-12$$$${\small (3)}~y’=3x^2-4$$$${\small (4)}~y’=6x^2-8x-6$$→ 微分の計算

p.186 練習10$${\small (1)}~0$$$${\small (2)}~0$$$${\small (3)}~24$$

p.187 練習11$${\small (1)}~s’=6t-4$$$${\small (2)}~f'(t)=3at^2+2bt$$

p.187 練習12$$~~~{ \frac{\,dV\,}{dr}}=4\pi r^2~,~{ \frac{\,dS\,}{dr}}=8\pi r$$

p.188
練習13$${\small (1)}~4$$$${\small (2)}~y=4x-5$$→ 接線の方程式①

p.189 練習14$$y=2x~,~y=-6x$$→ 接線の方程式②（外部の点から引いた接線）

p.192 練習15\({\small (1)}~\)
　\(x≦0\) で増加
　\(0≦x≦4\) で減少
　\(4≦x\) で増加
\({\small (2)}~\)
　\(x≦-2\) で減少
　\(-2≦x≦1\) で増加
　\(1≦x\) で減少

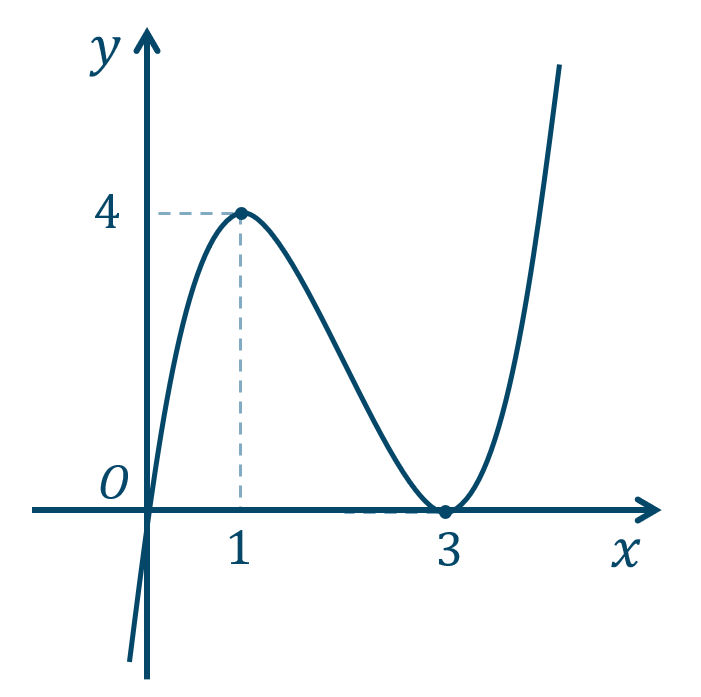
p.194 練習16\({\small (1)}~\)

\(x\)	\(\cdots\)	\(1\)	\(\cdots\)	\(3\)	\(\cdots\)
\(f'(x)\)	\(+\)	\(0\)	\(-\)	\(0\)	\(+\)
\(f(x)\)	↗︎	\(4\)	↘︎	\(0\)	↗︎

\(x=1\) で極大値 \(4\)
\(x=3\) で極小値 \(0\)

\({\small (2)}~\)

\(x\)	\(\cdots\)	\(0\)	\(\cdots\)	\(2\)	\(\cdots\)
\(f'(x)\)	\(-\)	\(0\)	\(+\)	\(0\)	\(-\)
\(f(x)\)	↘︎	\(0\)	↗︎	\(5\)	↘︎

\(x=2\) で極大値 \(5\)
\(x=0\) で極小値 \(1\)

\({\small (3)}~\)

\(x\)	\(\cdots\)	\(-2\)	\(\cdots\)	\(0\)	\(\cdots\)
\(f'(x)\)	\(+\)	\(0\)	\(-\)	\(0\)	\(+\)
\(f(x)\)	↗︎	\(8\)	↘︎	\(0\)	↗︎

\(x=-2\) で極大値 \(8\)
\(x=0\) で極小値 \(0\)

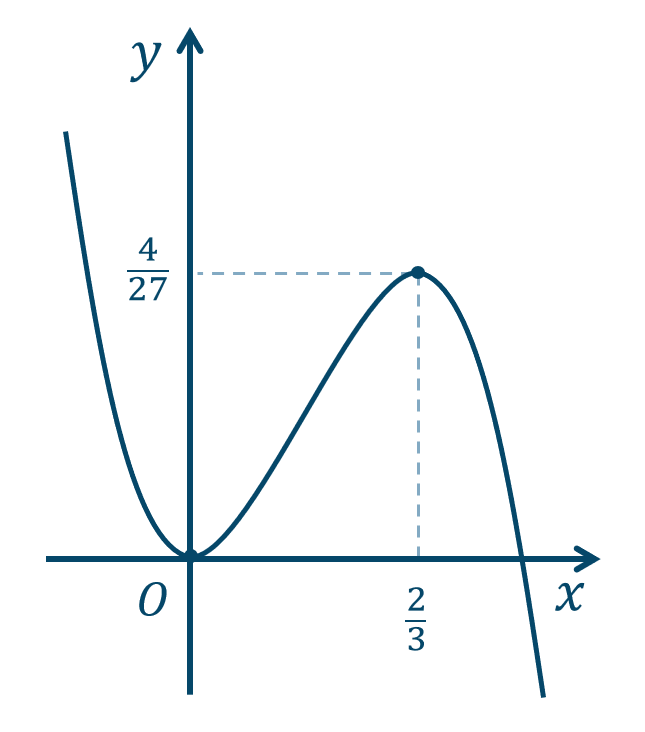
\({\small (4)}~\)

\(x\)	\(\cdots\)	\(0\)	\(\cdots\)	\({\large \frac{\,2\,}{\,3\,}}\)	\(\cdots\)
\(f'(x)\)	\(-\)	\(0\)	\(+\)	\(0\)	\(-\)
\(f(x)\)	↘︎	\(0\)	↗︎	\({\large \frac{\,4\,}{\,27\,}}\)	↘︎

\(x={\large \frac{2}{3}}\) で極大値 \({\large \frac{4}{27}}\)
\(x=0\) で極小値 \(0\)

→ ３次関数のグラフと増減表

p.194 練習17\({\small (1)}~\)\(f'(x)=-3x^2\) より、
\(f'(x)=0\) とすると \(x=0\)
\(f(x)\) の増減表は、

\(x\)	\(\cdots\)	\(0\)	\(\cdots\)
\(f'(x)\)	\(-\)	\(0\)	\(-\)
\(f(x)\)	↘︎	\(0\)	↘︎

これより、\(f(x)\) は常に減少して極値をもたない
 
\({\small (2)}~\)\(f'(x)=3x^2+1\) より、
\(3x^2≧0\) より、常に \(f'(x)>0\)
これより、\(f(x)\) は常に増加して極値をもたない

p.195 練習18　\(a=-3~,~b=3\)、極小値 \(-24\)
→ 極値の条件と関数の決定

p.196 研究 練習1$${\small (1)}~y’=4x^3-1$$$${\small (2)}~y’=-8x^3-3x^2+3$$

p.196 研究 練習2\({\small (1)}~\)
　\(x=-2\) で極小値 \(-27\)
　\(x=0\) で極大値 \(5\)
　\(x=1\) で極小値 \(0\)

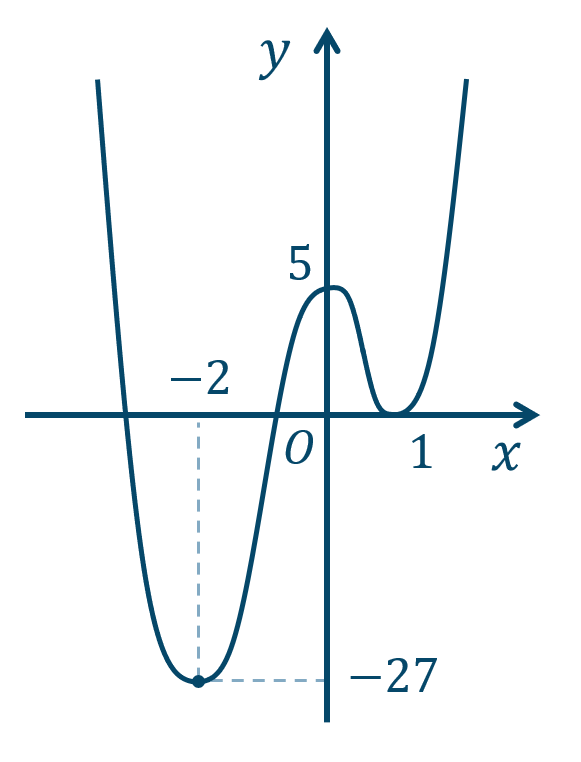
\({\small (2)}~\)
　\(x=0\) で極大値 \(2\)
　\(x=\pm2\) で極小値 \(-14\)

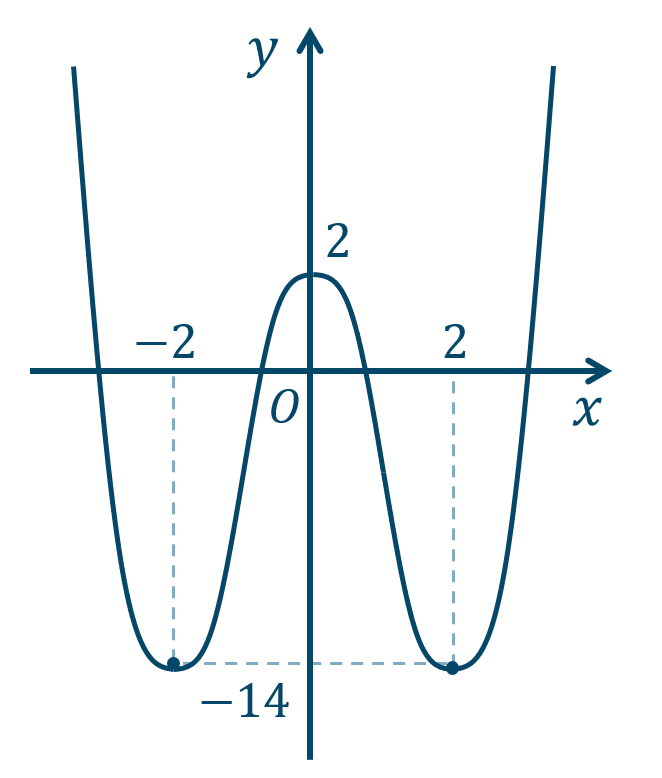
→ ４次関数のグラフと増減表

p.197 練習19\({\small (1)}~\)
　\(x=2\) で最大値 \(20\)
　\(x=-3~,~0\) で最小値 \(0\)
\({\small (2)}~\)
　\(x=-2~,~1\) で最大値 \(3\)
　\(x=-1~,~2\) で最小値 \(-1\)
\({\small (3)}~\)
　\(x=-1\) で最大値 \(8\)
　\(x=2\) で最小値 \(-46\)
→ ３次関数の最大値・最小値

p.197 深める① 平方完成すると、$$~~~y=(x-2)^2-2$$よって、\(x=2\) のとき最小値 \(-2\)
 
② 微分すると、\(y’=2x-4\)
\(y’=0\) とすると、\(x=2\)
増減表をかくと、

\(x\)	\(\cdots\)	\(2\)	\(\cdots\)
\(f'(x)\)	\(-\)	\(0\)	\(+\)
\(f(x)\)	↘︎	\(-2\)	↗︎

これより、\(x=2\) のとき最小値 \(-2\)

p.198 練習20$$~~~2~{\rm cm}$$

p.199 練習21\({\small (1)}~\)１個
\({\small (2)}~\)３個
\({\small (3)}~\)２個
→ ３次方程式の解の個数①

p.200 練習22[証明]
\(f(x)=(x^3+3x^2+5)-9x\) とすると、$$\begin{eqnarray}~~~f'(x)&=&3x^2+6x-9\\[2pt]~~~&=&3(x+3)(x-1)\end{eqnarray}$$よって、\(x≧0\) での増減表は

\(x\)	\(0\)	\(\cdots\)	\(1\)	\(\cdots\)
\(f'(x)\)		\(-\)	\(0\)	\(+\)
\(f(x)\)	\(5\)	↘︎	\(0\)	↗︎

よって、\(x≧0\) で最小値が \(0\) であるので、
　\(f(x)≧0\)
したがって、\(x≧0\) のとき
　\(x^3+3x^2+5≧9x\)
また、等号が成り立つときは \(x=1\) のとき [終]
→ ３次不等式の証明

p.202 練習23　②、④

p.203 練習24[証明]
\(n\) が \(0\) または正の整数のとき、$$~~~F(x)={ \frac{1}{\,n+1\,}}x^{n+1}$$とすると、$$~~~F'(x)=(n+1)\cdot{ \frac{1}{\,n+1\,}}x^{n}=x^n$$よって、\(x^n\) の不定積分の１つは \(F(x)\) である
したがって、$$~~~\int x^n dx={ \frac{1}{\,n+1\,}}x^{n+1}+C$$[終]
 
また、\(C\) を積分定数として$$~~~\int x^3 dx={ \frac{1}{\,4\,}}x^4+C$$

p.204 練習25\(C\) を積分定数として、$${\small (1)}~2x^3+C$$$${\small (2)}~{ \frac{1}{\,3\,}}x^3+{ \frac{1}{\,2\,}}x^2-x+C$$$${\small (3)}~x^3-x^2+5x+C$$$${\small (4)}~-{ \frac{2}{\,3\,}}x^3-{ \frac{1}{\,2\,}}x^2+7x+C$$

p.205 練習26\(C\) を積分定数として、$${\small (1)}~{ \frac{2}{\,3\,}}t^3-{ \frac{\,3\,}{2}}t^2-4t+C$$$${\small (2)}~y^3+{ \frac{\,5\,}{2}}y^2-2y+C$$→ 不定積分

p.205 練習27$$~~~F(x)=x^3-4x+2$$→ 不定積分と関数の決定

p.207 練習28$${\small (1)}~4$$$${\small (2)}~3$$$${\small (3)}~-6$$

p.207 練習29$${\small (1)}~{ \frac{2}{\,3\,}}$$$${\small (2)}~-{ \frac{1}{\,6\,}}$$→ 定積分の計算

p.208 練習30$${\small (1)}~-{ \frac{\,9\,}{2}}$$$${\small (2)}~-{ \frac{\,68\,}{3}}$$

p.208 練習31$$~~~0$$

p.209 練習32$${\small (1)}~10$$$${\small (2)}~{ \frac{\,4\,}{3}}$$→ 定積分の計算

p.210 練習33$$~~~3x^2-2x-1$$→ 定積分で表された関数

p.210 練習34$$~~~f(x)=2x-1~,~a=-1~,~2$$→ 定積分で表された関数

p.213 練習35$${\small (1)}~{ \frac{\,26\,}{3}}$$$${\small (2)}~9$$→ 定積分と面積③（区間付きの面積）

p.214 練習36$${\small (1)}~{ \frac{\,4\,}{3}}$$$${\small (2)}~{ \frac{\,4\,}{3}}$$→ 定積分と面積①（x軸と囲まれた面積）

p.214 深める$$\begin{split}&\int_{0}^{a}\left(\frac{\,b\,}{\,a\,}x\right)dx\\[3pt]~~=~&\left[ \frac{\,b\,}{\,2a\,}x^2 \right]_{0}^{a}=\frac{\,b\,}{\,2a\,}\times a^2=\frac{\,1\,}{\,2\,}ab\end{split}$$

p.216 練習37$$~~~{ \frac{\,11\,}{3}}$$

p.216 練習38$${\small (1)}~{ \frac{\,9\,}{2}}$$$${\small (2)}~{ \frac{\,32\,}{3}}$$→ 定積分と面積②（２つの関数で囲まれた面積）

p.218 研究 練習1$${\small (1)}~x^4+2x^3+3x+C$$$${\small (2)}~-{ \frac{3}{\,4\,}}$$

p.218 研究 2$$~~~{ \frac{\,37\,}{12}}$$

p.221 章末問題Ｂ 15\(0≦x≦1\) の区間ではグラフが \(x\) 軸より下にくるので、定積分にマイナスを付ける
正しい式と答えは、$$~~~S=\int_{-1}^{0}(x^3-x)dx-\int_{0}^{1}(x^3-x)dx$$$$~~~~~~=\frac{\,1\,}{\,2\,}$$