文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
第1章 式と証明
第2章 複素数と方程式
第3章 図形と方程式
第5章 指数関数と対数関数
第6章 微分法と積分法
第4章 三角関数
第1節 三角関数
p.109 練習1
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

\({\small (5)}~\)

\({\small (1)}~\)

\({\small (2)}~\)
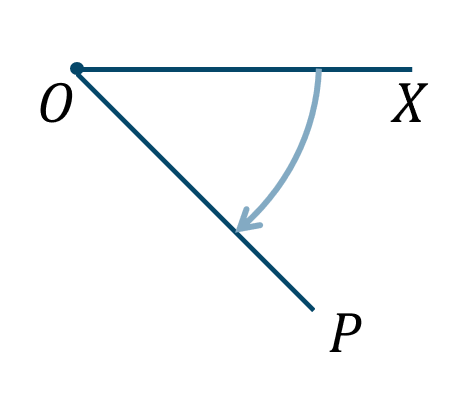
\({\small (3)}~\)
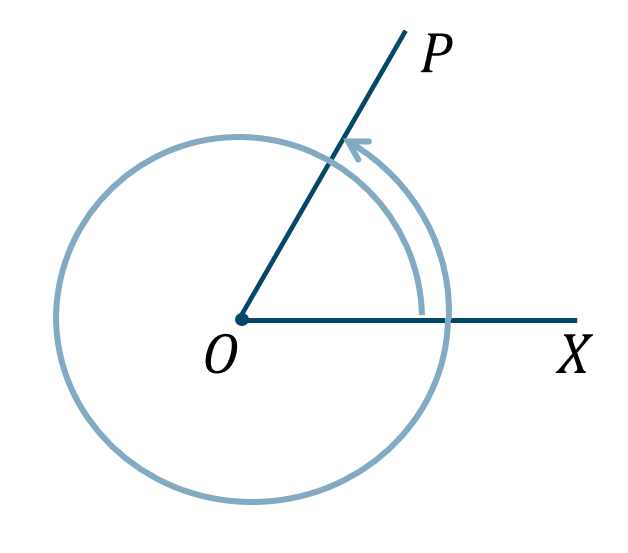
\({\small (4)}~\)
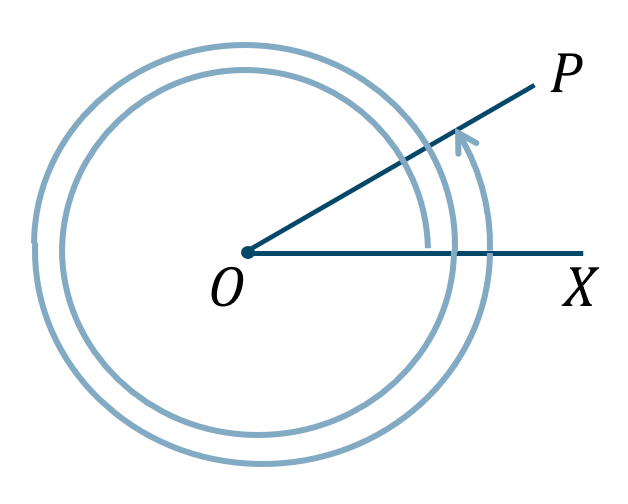
\({\small (5)}~\)
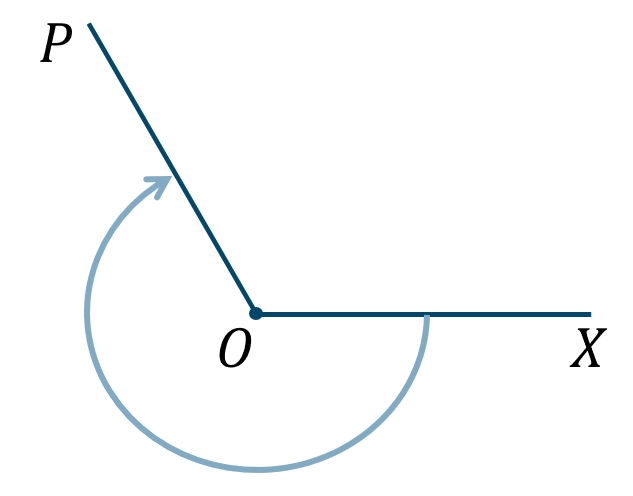
p.110 練習3
\({\small (1)}~\)
[証明]
弧の長さ \(1\) に対する中心角の大きさが \(1\) ラジアンである
中心角 \(180^\circ\) の弧は半円となるので、弧の長さは、
\(2\pi \times {\large \frac{1}{2}}=\pi\)
したがって、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンである
[終]
\({\small (2)}~\)
[証明]
\(1\) ラジアンに対する中心角の大きさを \(a^\circ\) とする
(1) の結果より、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンであるので、
\(\pi:180^\circ=1:a^\circ\)
よって、
\(a={\large \frac{180}{\pi}}\)
したがって、
\(1\) ラジアンは \(\left({\large \frac{180}{\pi}}\right)^\circ\)
[終]
\({\small (1)}~\)
[証明]
弧の長さ \(1\) に対する中心角の大きさが \(1\) ラジアンである
中心角 \(180^\circ\) の弧は半円となるので、弧の長さは、
\(2\pi \times {\large \frac{1}{2}}=\pi\)
したがって、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンである
[終]
\({\small (2)}~\)
[証明]
\(1\) ラジアンに対する中心角の大きさを \(a^\circ\) とする
(1) の結果より、弧の長さ \(\pi\) に対する中心角の大きさは \(\pi\) ラジアンであるので、
\(\pi:180^\circ=1:a^\circ\)
よって、
\(a={\large \frac{180}{\pi}}\)
したがって、
\(1\) ラジアンは \(\left({\large \frac{180}{\pi}}\right)^\circ\)
[終]
p.110 練習4
\({\small (1)}~{\large \frac{7}{6}}\pi\) \({\small (2)}~{\large \frac{4}{3}}\pi\) \({\small (3)}~{\large \frac{11}{6}}\pi\)
\({\small (4)}~225^\circ\) \({\small (5)}~270^\circ\)
→ 弧度法と扇形
\({\small (1)}~{\large \frac{7}{6}}\pi\) \({\small (2)}~{\large \frac{4}{3}}\pi\) \({\small (3)}~{\large \frac{11}{6}}\pi\)
\({\small (4)}~225^\circ\) \({\small (5)}~270^\circ\)
→ 弧度法と扇形
p.111 練習5
\({\small (1)}~l={\large \frac{4}{3}}\pi~,~S={\large \frac{8}{3}}\pi\)
\({\small (2)}~l=7\pi~,~S=21\pi\)
→ 弧度法と扇形
\({\small (1)}~l={\large \frac{4}{3}}\pi~,~S={\large \frac{8}{3}}\pi\)
\({\small (2)}~l=7\pi~,~S=21\pi\)
→ 弧度法と扇形
p.113 練習6
\({\small (1)}~\)
\(\sin{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{5}{4}}\pi}=1\)
\({\small (2)}~\)
\(\sin{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{2}}~,~\cos{{\large \frac{11}{6}}\pi}={\large \frac{\sqrt{3}}{2}}\)
\(\tan{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{\sqrt{3}}}\)
\({\small (3)}~\)
\(\sin{\left(-{\large \frac{\pi}{3}}\right)}=-{\large \frac{\sqrt{3}}{2}}~,~\cos{\left(-{\large \frac{\pi}{3}}\right)}={\large \frac{1}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{3}}\right)}=-\sqrt{3}\)
→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
\({\small (1)}~\)
\(\sin{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}~,~\cos{{\large \frac{5}{4}}\pi}=-{\large \frac{1}{\sqrt{2}}}\)
\(\tan{{\large \frac{5}{4}}\pi}=1\)
\({\small (2)}~\)
\(\sin{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{2}}~,~\cos{{\large \frac{11}{6}}\pi}={\large \frac{\sqrt{3}}{2}}\)
\(\tan{{\large \frac{11}{6}}\pi}=-{\large \frac{1}{\sqrt{3}}}\)
\({\small (3)}~\)
\(\sin{\left(-{\large \frac{\pi}{3}}\right)}=-{\large \frac{\sqrt{3}}{2}}~,~\cos{\left(-{\large \frac{\pi}{3}}\right)}={\large \frac{1}{2}}\)
\(\tan{\left(-{\large \frac{\pi}{3}}\right)}=-\sqrt{3}\)
→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
p.113 練習7
\({\small (1)}~\)第4象限 \({\small (2)}~\)第3象限
\({\small (1)}~\)第4象限 \({\small (2)}~\)第3象限
p.114 練習8
\(\cos{\theta}={\large \frac{2\sqrt{2}}{3}}~,~\tan{\theta}=-{\large \frac{1}{2\sqrt{2}}}\)
\(\cos{\theta}={\large \frac{2\sqrt{2}}{3}}~,~\tan{\theta}=-{\large \frac{1}{2\sqrt{2}}}\)
p.114 練習9
\(\cos{\theta}=-{\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}=-{\large \frac{2}{\sqrt{5}}}\)
→ 三角関数の相互関係の公式
\(\cos{\theta}=-{\large \frac{1}{\sqrt{5}}}~,~\sin{\theta}=-{\large \frac{2}{\sqrt{5}}}\)
→ 三角関数の相互関係の公式
p.115 練習11
[証明]
(左辺)$$=\tan^2{\theta}-\sin^2{\theta}$$$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}-\sin^2{\theta}$$$$=\frac{\sin^2{\theta}-\sin^2{\theta}\cos^2{\theta}}{\cos^2{\theta}}$$$$=\frac{\sin^2{\theta}(1-\cos^2{\theta})}{\cos^2{\theta}}$$$$=\frac{\sin^2{\theta}\cdot\sin^2{\theta}}{\cos^2{\theta}}$$$$=\frac{\sin^4{\theta}}{\cos^2{\theta}}$$ (右辺)$$=\tan^2{\theta}\sin^2{\theta}$$$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}\cdot\sin^2{\theta}$$$$=\frac{\sin^4{\theta}}{\cos^2{\theta}}$$したがって、
\(\tan^2{\theta}-\sin^2{\theta}=\tan^2{\theta}\sin^2{\theta}\)
[終]
→ 三角関数の等式の証明
[証明]
(左辺)$$=\tan^2{\theta}-\sin^2{\theta}$$$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}-\sin^2{\theta}$$$$=\frac{\sin^2{\theta}-\sin^2{\theta}\cos^2{\theta}}{\cos^2{\theta}}$$$$=\frac{\sin^2{\theta}(1-\cos^2{\theta})}{\cos^2{\theta}}$$$$=\frac{\sin^2{\theta}\cdot\sin^2{\theta}}{\cos^2{\theta}}$$$$=\frac{\sin^4{\theta}}{\cos^2{\theta}}$$ (右辺)$$=\tan^2{\theta}\sin^2{\theta}$$$$=\frac{\sin^2{\theta}}{\cos^2{\theta}}\cdot\sin^2{\theta}$$$$=\frac{\sin^4{\theta}}{\cos^2{\theta}}$$したがって、
\(\tan^2{\theta}-\sin^2{\theta}=\tan^2{\theta}\sin^2{\theta}\)
[終]
→ 三角関数の等式の証明
p.119 練習12
\({\small (1)}~\)

周期 \(2\pi\)
\({\small (2)}~\)

周期 \(2\pi\)
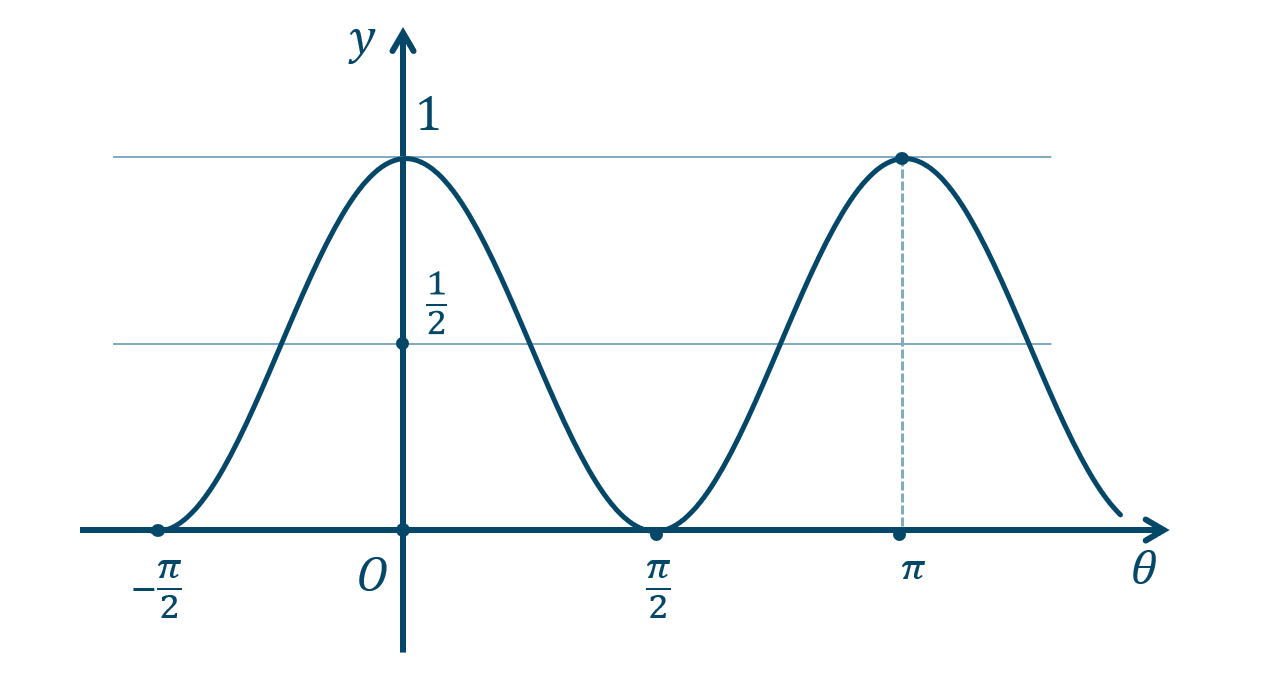
\({\small (3)}~\)

周期 \(\pi\)
→ 三角関数のグラフ④(平行移動)
\({\small (1)}~\)
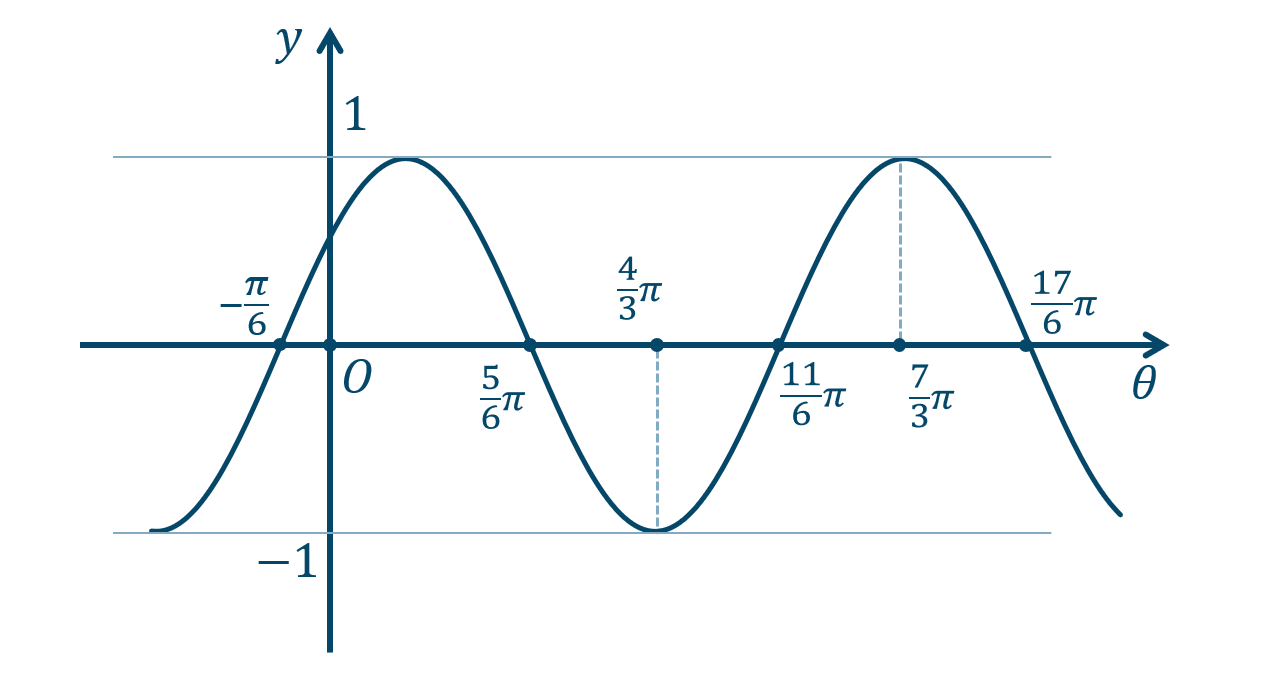
周期 \(2\pi\)
\({\small (2)}~\)
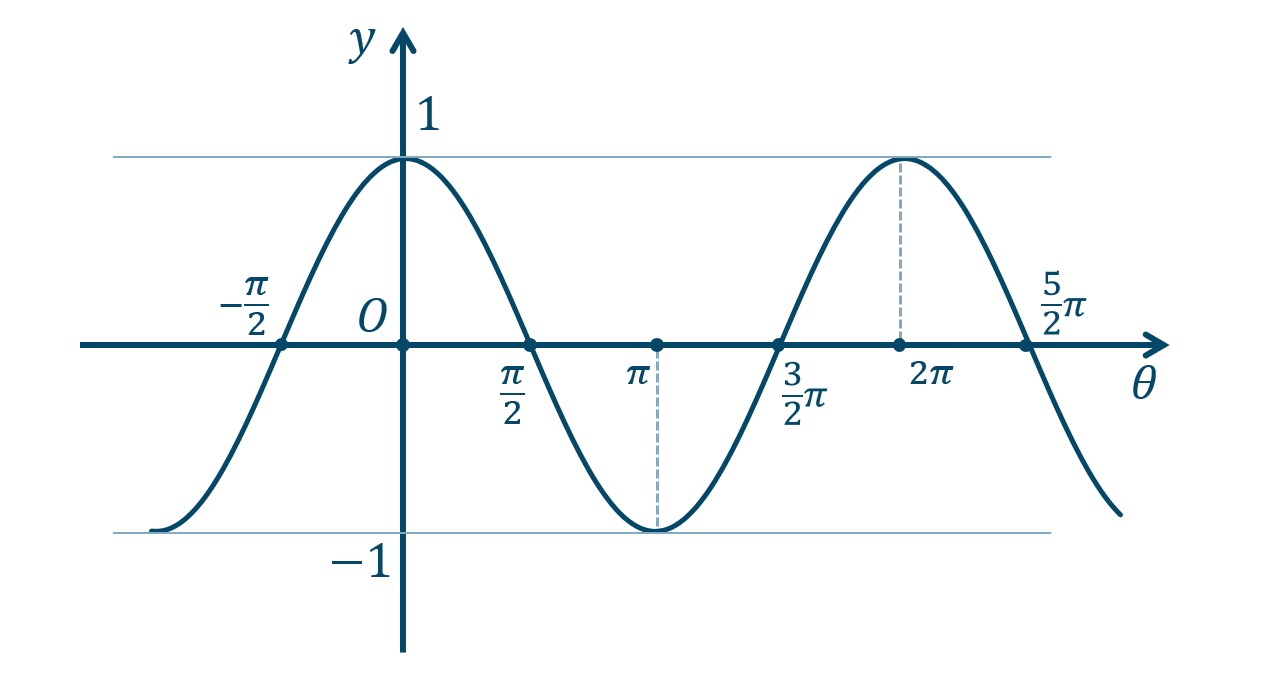
周期 \(2\pi\)
\({\small (3)}~\)
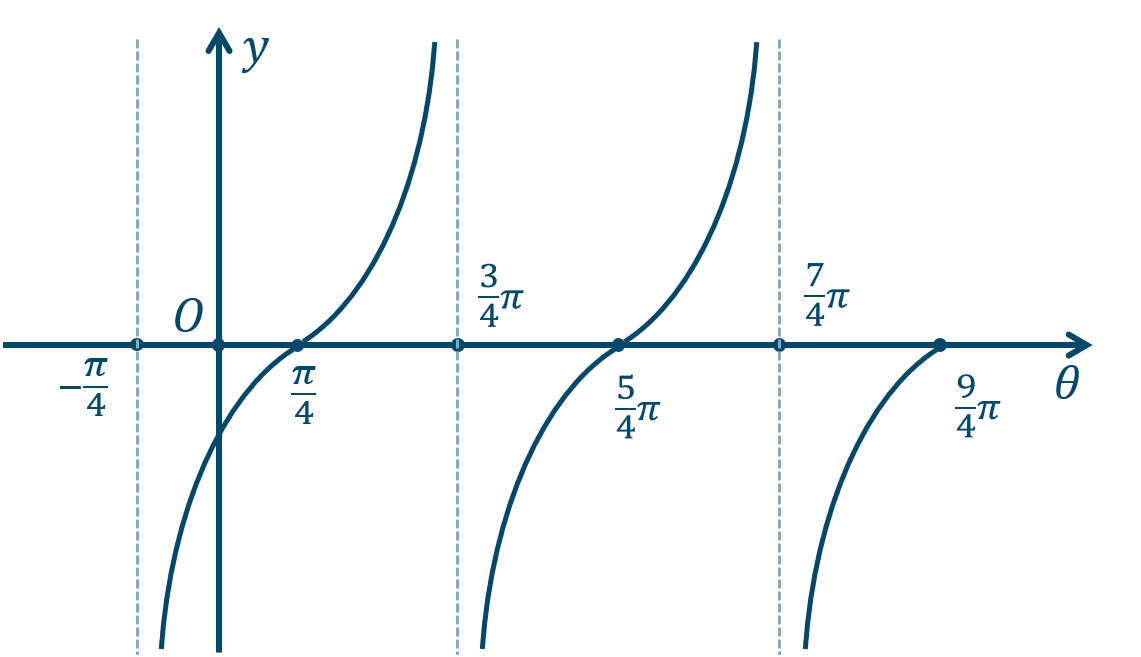
周期 \(\pi\)
→ 三角関数のグラフ④(平行移動)
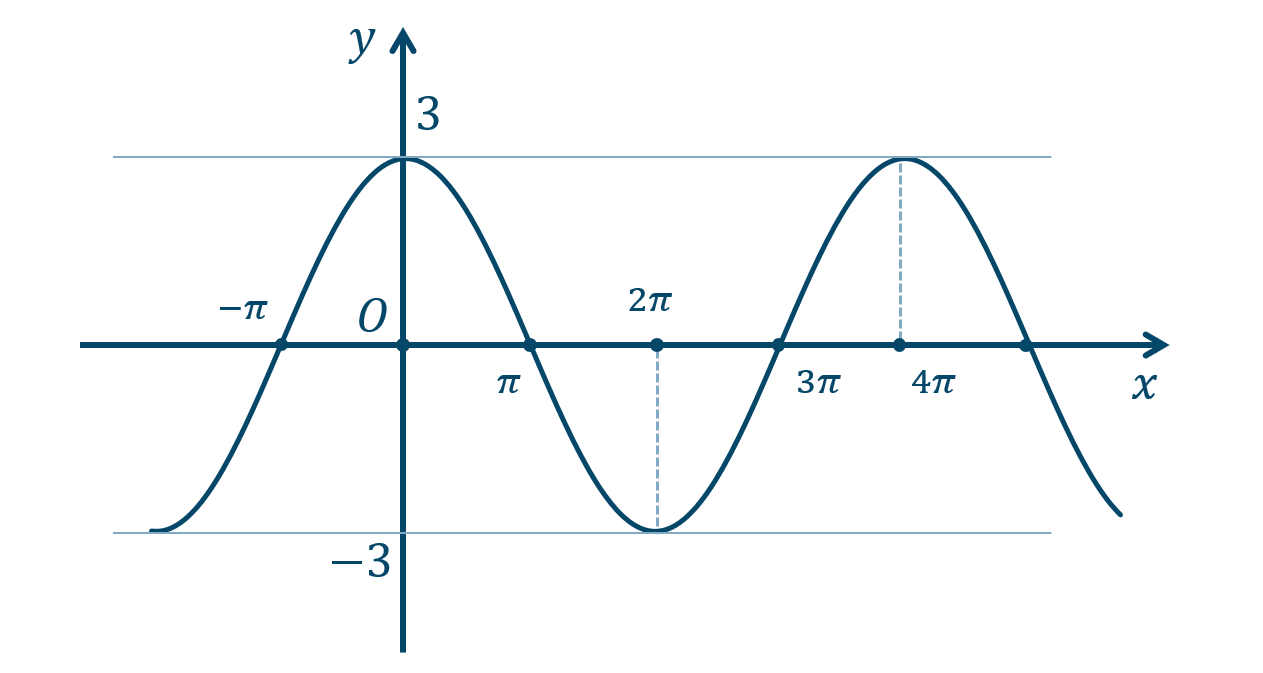
p.119 練習13
\({\small (1)}~\)

周期 \(2\pi\)
\({\small (2)}~\)

周期 \(2\pi\)
\({\small (3)}~\)

周期 \(\pi\)
→ 三角関数のグラフ②(縦幅の変化)
\({\small (1)}~\)
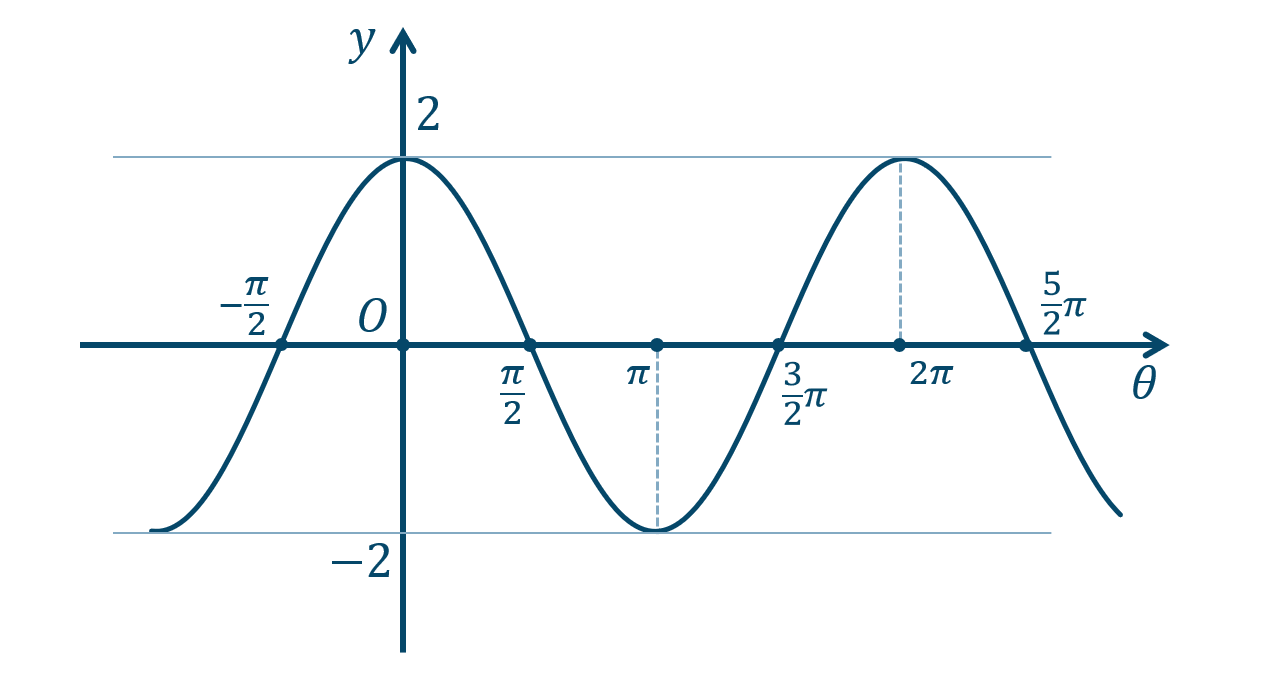
周期 \(2\pi\)
\({\small (2)}~\)
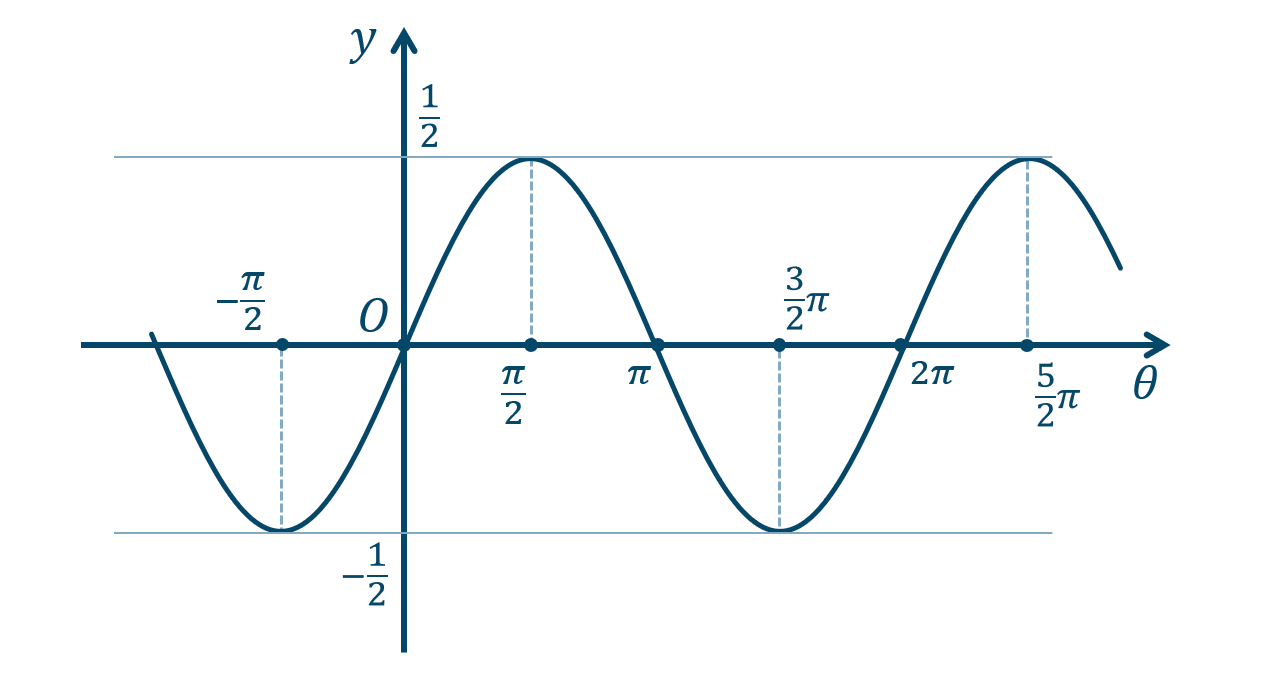
周期 \(2\pi\)
\({\small (3)}~\)
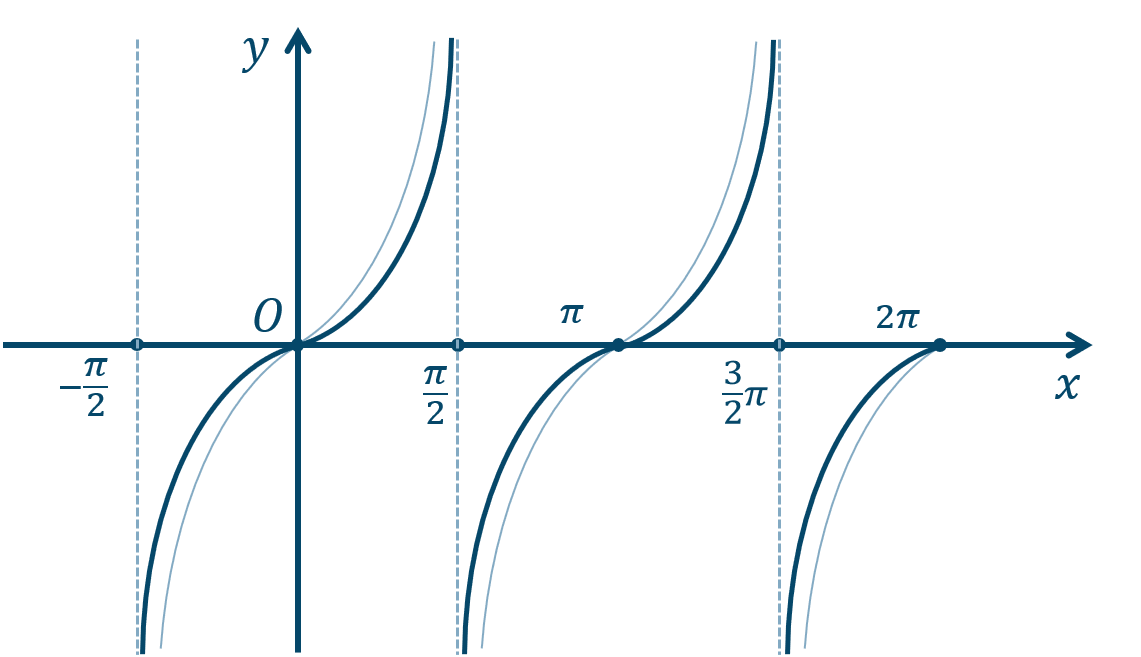
周期 \(\pi\)
→ 三角関数のグラフ②(縦幅の変化)
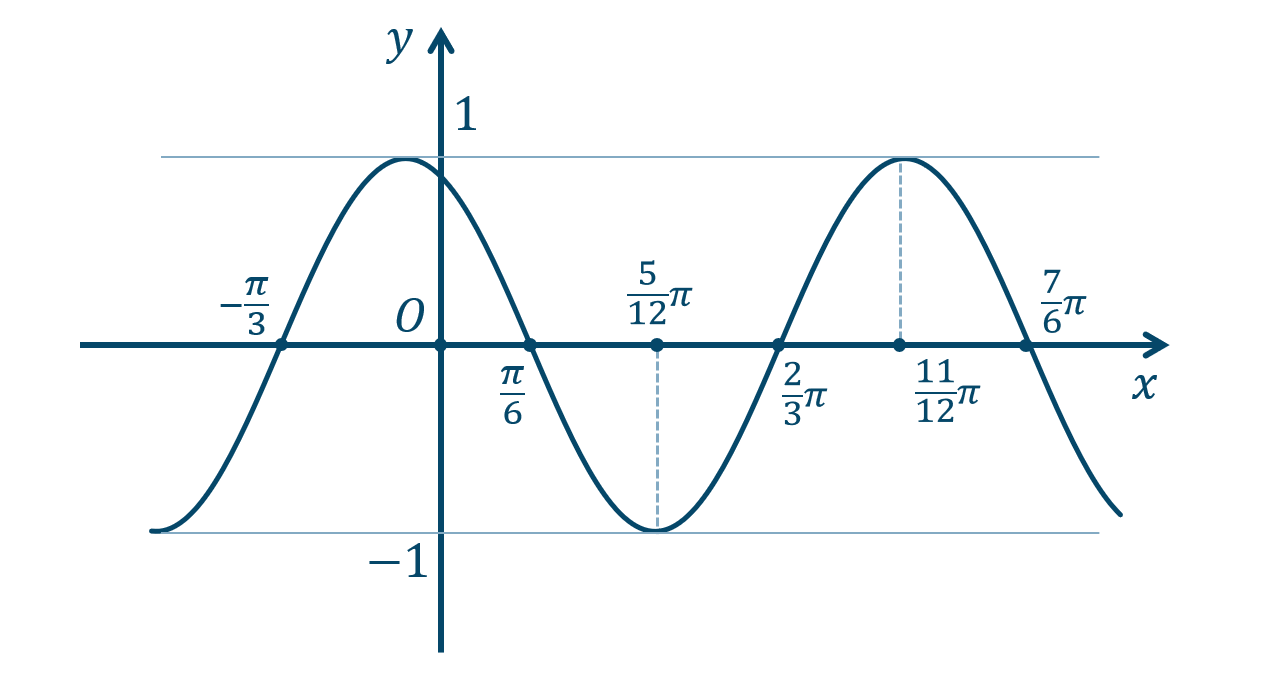
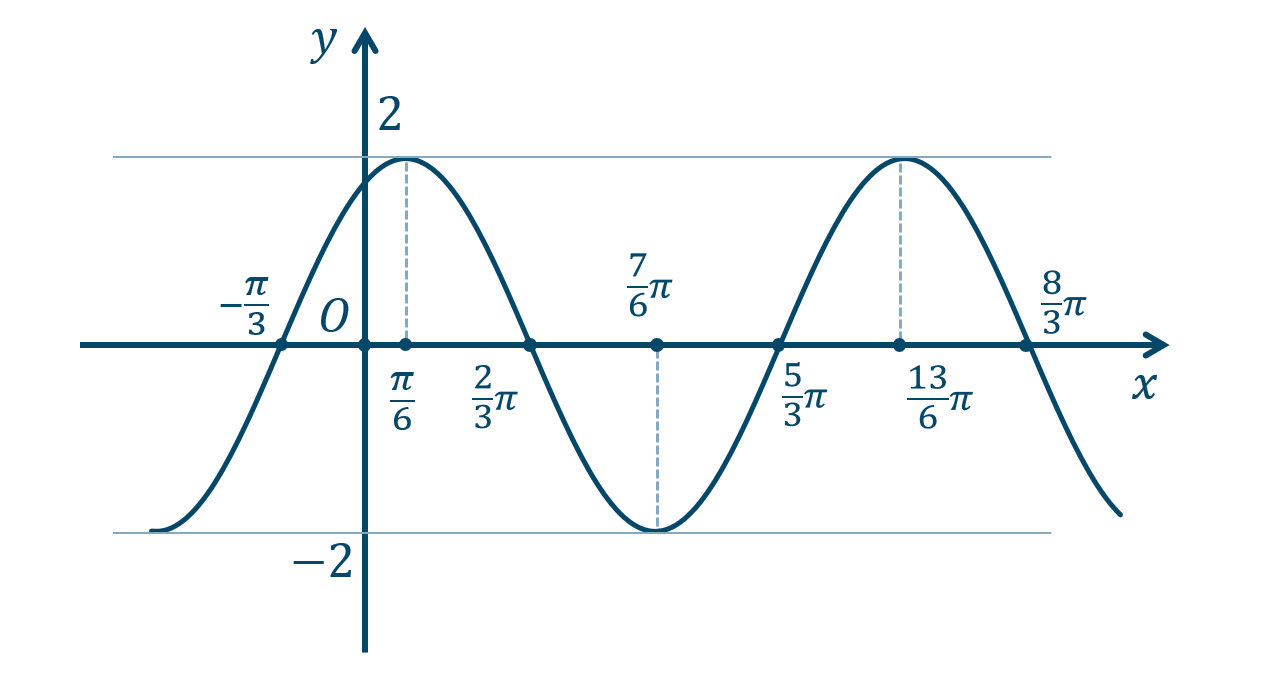
p.120 練習14
\({\small (1)}~\)

周期 \(\pi\)
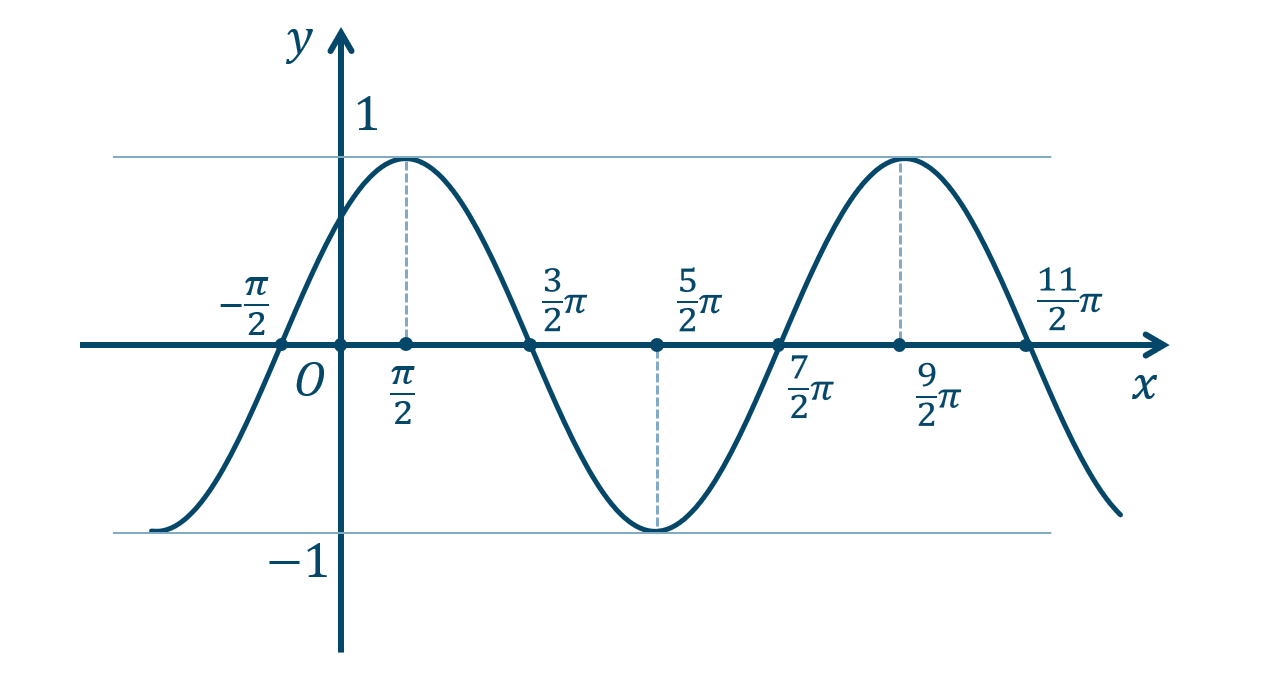
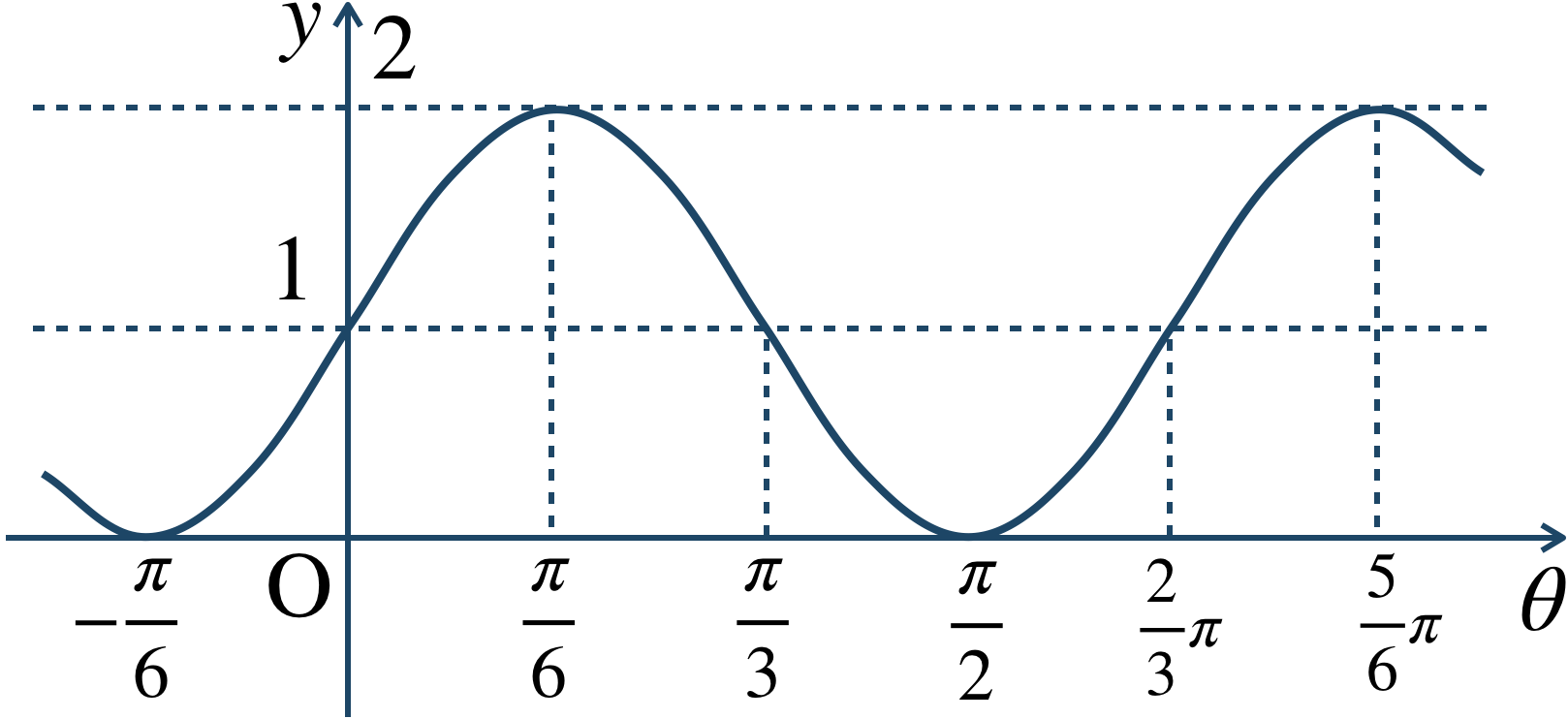
\({\small (2)}~\)

周期 \(4\pi\)
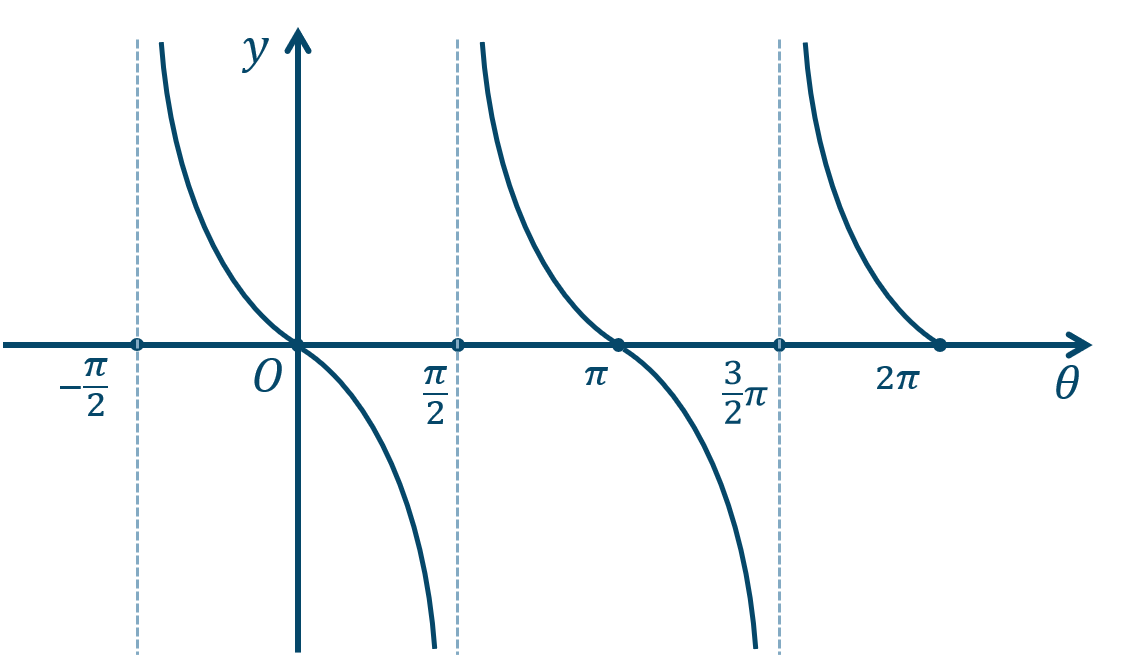
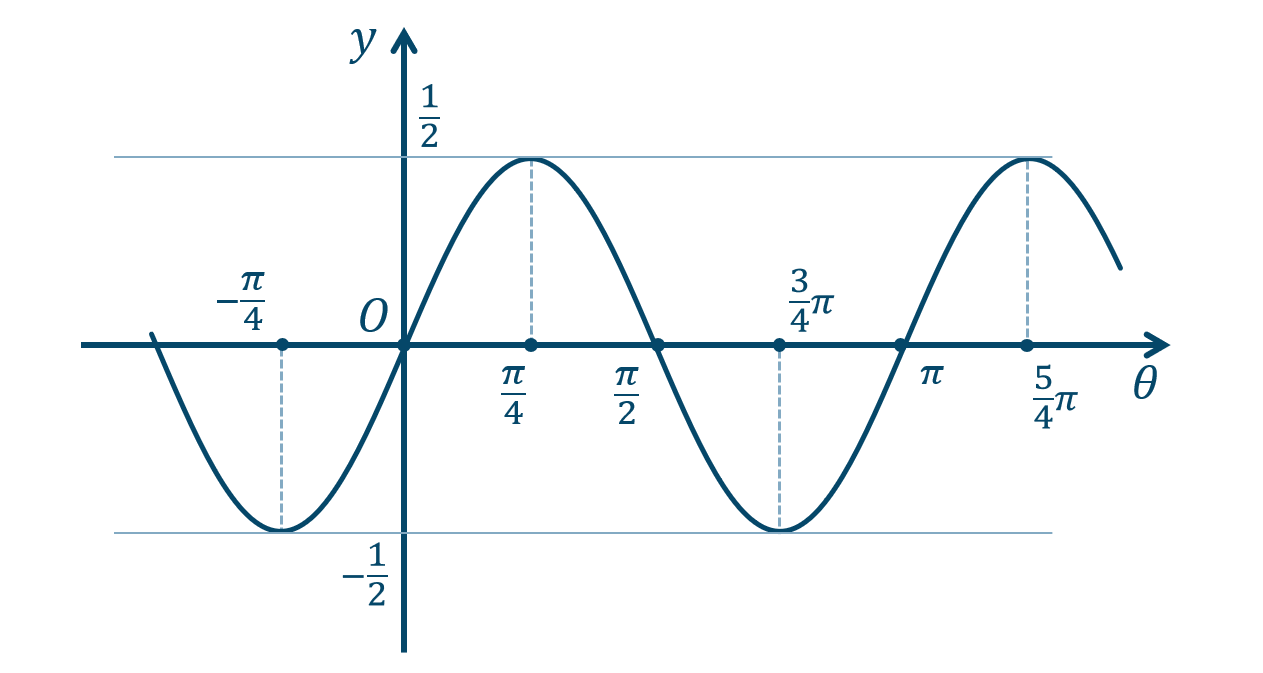
\({\small (3)}~\)

周期 \({\large \frac{\pi}{2}}\)
→ 三角関数のグラフ③(周期の変化)
\({\small (1)}~\)
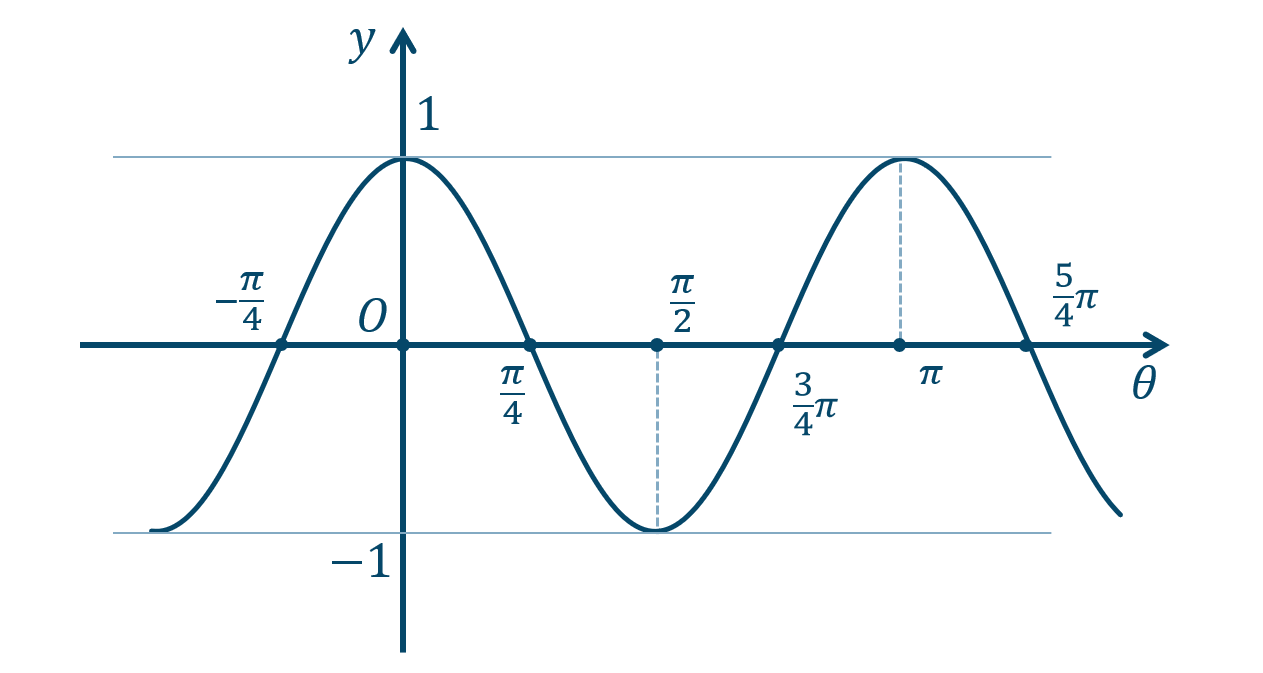
周期 \(\pi\)
\({\small (2)}~\)
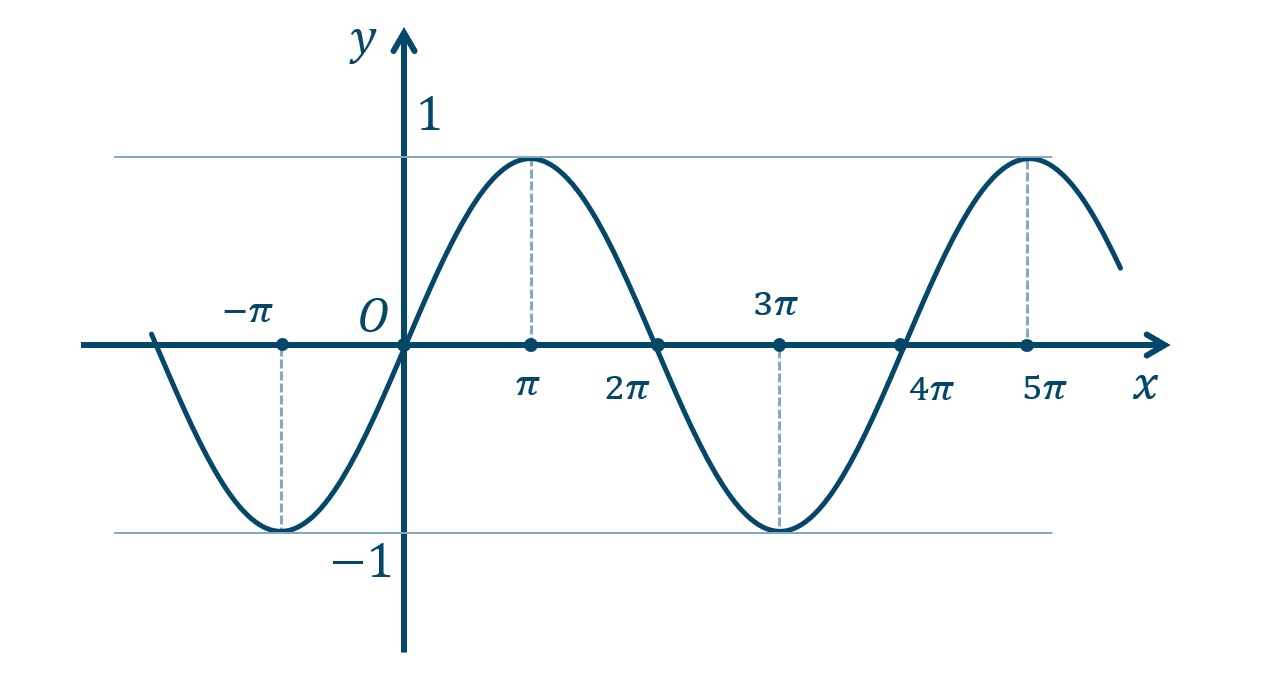
周期 \(4\pi\)
\({\small (3)}~\)
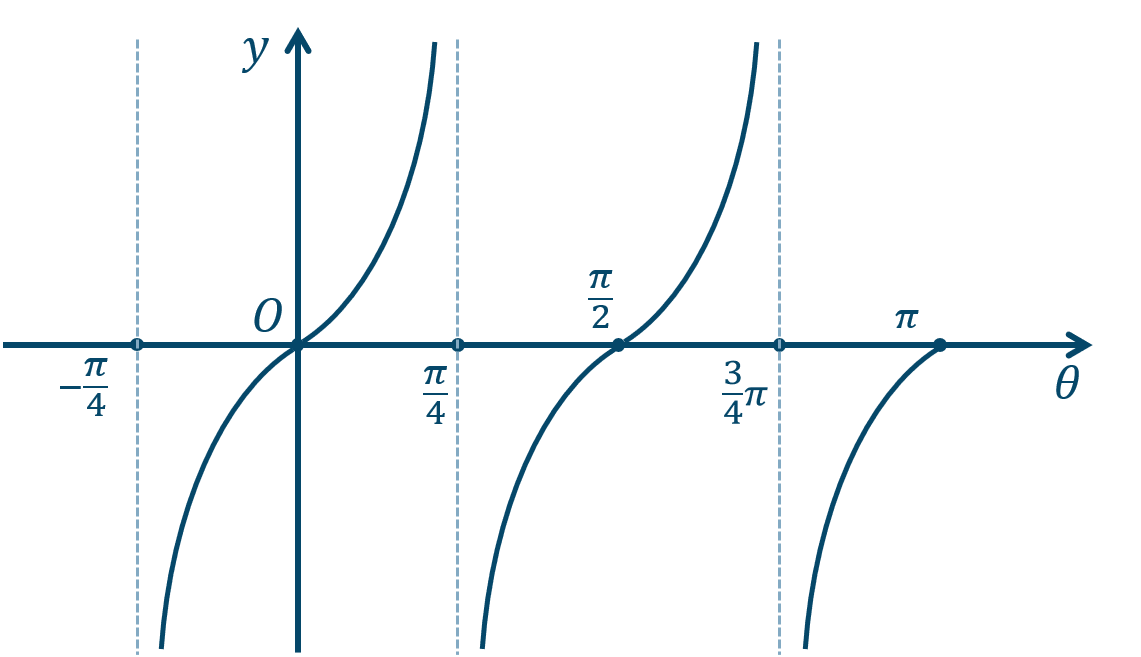
周期 \({\large \frac{\pi}{2}}\)
→ 三角関数のグラフ③(周期の変化)
p.123 練習16
\({\small (1)}~-{\large \frac{1}{2}}\) \({\small (2)}~{\large \frac{\sqrt{3}}{2}}\) \({\small (3)}~-1\)
→ 三角関数の性質①
→ 三角関数の性質②
\({\small (1)}~-{\large \frac{1}{2}}\) \({\small (2)}~{\large \frac{\sqrt{3}}{2}}\) \({\small (3)}~-1\)
→ 三角関数の性質①
→ 三角関数の性質②
p.124 練習17
\({\small (1)}~\theta={\large \frac{\pi}{3}}~,~{\large \frac{2}{3}}\pi\)
\({\small (2)}~\theta={\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi\)
\({\small (3)}~\theta={\large \frac{3}{2}}\pi\)
\({\small (1)}~\theta={\large \frac{\pi}{3}}~,~{\large \frac{2}{3}}\pi\)
\({\small (2)}~\theta={\large \frac{2}{3}}\pi~,~{\large \frac{4}{3}}\pi\)
\({\small (3)}~\theta={\large \frac{3}{2}}\pi\)
p.124 練習18
\({\small (1)}~\theta={\large \frac{4}{3}}\pi+2n\pi~,~{\large \frac{5}{3}}\pi+2n\pi\)
ただし、\(n\) は整数
\({\small (2)}~\theta={\large \frac{3}{4}}\pi+2n\pi~,~{\large \frac{5}{4}}\pi+2n\pi\)
ただし、\(n\) は整数
\({\small (1)}~\theta={\large \frac{4}{3}}\pi+2n\pi~,~{\large \frac{5}{3}}\pi+2n\pi\)
ただし、\(n\) は整数
\({\small (2)}~\theta={\large \frac{3}{4}}\pi+2n\pi~,~{\large \frac{5}{4}}\pi+2n\pi\)
ただし、\(n\) は整数
p.125 練習19
\(\theta={\large \frac{2}{3}}\pi~,~{\large \frac{5}{3}}\pi\)
\(\theta={\large \frac{2}{3}}\pi+n\pi\)
ただし、\(n\) は整数
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
\(\theta={\large \frac{2}{3}}\pi~,~{\large \frac{5}{3}}\pi\)
\(\theta={\large \frac{2}{3}}\pi+n\pi\)
ただし、\(n\) は整数
→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
p.125 練習20
\({\small (1)}~\theta={\large \frac{17}{12}}\pi~,~{\large \frac{23}{12}}\pi\)
\({\small (2)}~\theta={\large \frac{19}{12}}\pi~,~{\large \frac{23}{12}}\pi\)
→ 三角関数を含む方程式②(範囲変化)
\({\small (1)}~\theta={\large \frac{17}{12}}\pi~,~{\large \frac{23}{12}}\pi\)
\({\small (2)}~\theta={\large \frac{19}{12}}\pi~,~{\large \frac{23}{12}}\pi\)
→ 三角関数を含む方程式②(範囲変化)
p.126 練習21
\({\small (1)}~{\large \frac{\pi}{3}}≦\theta≦{\large \frac{5}{3}}\pi\)
\({\small (2)}~{\large \frac{\pi}{4}}<\theta<{\large \frac{3}{4}}\pi\)
\({\small (3)}~0≦\theta<{\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi<\theta<2\pi\)
\({\small (1)}~{\large \frac{\pi}{3}}≦\theta≦{\large \frac{5}{3}}\pi\)
\({\small (2)}~{\large \frac{\pi}{4}}<\theta<{\large \frac{3}{4}}\pi\)
\({\small (3)}~0≦\theta<{\large \frac{\pi}{6}}~,~{\large \frac{5}{6}}\pi<\theta<2\pi\)
p.127 練習22
\(0≦\theta≦{\large \frac{\pi}{3}}~,~{\large \frac{\pi}{2}}<\theta≦{\large \frac{4}{3}}\pi\)
\({\large \frac{3}{2}}\pi<\theta<2\pi\)
→ 三角関数を含む不等式①
\(0≦\theta≦{\large \frac{\pi}{3}}~,~{\large \frac{\pi}{2}}<\theta≦{\large \frac{4}{3}}\pi\)
\({\large \frac{3}{2}}\pi<\theta<2\pi\)
→ 三角関数を含む不等式①
p.128 練習23
\(\theta=\pi\) で最大値 \(2\)
\(\theta={\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi\) で最小値 \(-{\large \frac{1}{4}}\)
→ 三角関数を含む2次関数
\(\theta=\pi\) で最大値 \(2\)
\(\theta={\large \frac{\pi}{3}}~,~{\large \frac{5}{3}}\pi\) で最小値 \(-{\large \frac{1}{4}}\)
→ 三角関数を含む2次関数
問題