このページは、東京書籍:Advanced数学Ⅱ[701]
3章 三角関数
3章 三角関数

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介 高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学Ⅱ 1章 方程式・式と証明
Advanced数学Ⅱ 2章 図形と方程式
Advanced数学Ⅱ 3章 三角関数
Advanced数学Ⅱ 4章 指数関数・対数関数
Advanced数学Ⅱ 5章 微分と積分
3章 三角関数
1節 三角関数
p.115 問1\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

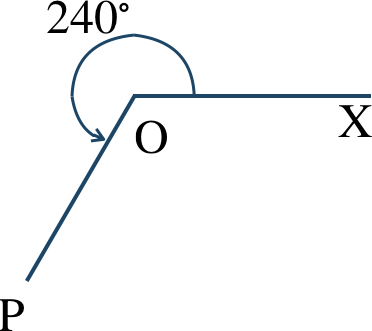
\({\small (2)}~\)

\({\small (3)}~\)
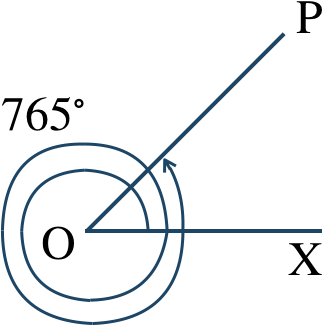
\({\small (4)}~\)

p.115 問2以下 \(n\) は整数$${\small (1)}~140^\circ+360^\circ\times n$$$${\small (2)}~280^\circ+360^\circ\times n$$$${\small (3)}~70^\circ+360^\circ\times n$$$${\small (4)}~250^\circ+360^\circ\times n$$→ 動径と一般角
p.116 問3$$~~~-{ \frac{\,3\,}{2}}\pi~,~{ \frac{\,9\,}{4}}\pi~,~{ \frac{1}{\,180\,}}\pi$$
p.116 問4$$~~~36^\circ~,~-450^\circ~,~-540^\circ$$
p.116 問5$$~~~l={ \frac{\,9\,}{2}}\pi~,~S={ \frac{\,27\,}{2}}\pi$$→ 弧度法と扇形
p.117 問6$${\small (1)}~\sin{{ \frac{\,5\,}{4}}\pi}=-{\ \frac{1}{\,\sqrt{2}\,}}$$$$~~~~~\cos{{ \frac{\,5\,}{4}}\pi}=-{ \frac{1}{\,\sqrt{2}\,}}$$$$~~~~~\tan{{ \frac{\,5\,}{4}}\pi}=1$$$${\small (2)}~\sin{{ \frac{\,11\,}{6}}\pi}=-{ \frac{1}{\,2\,}}$$$$~~~~~\cos{{ \frac{\,11\,}{6}}\pi}={ \frac{\,\sqrt{3}\,}{2}}$$$$~~~~~\tan{{ \frac{\,11\,}{6}}\pi}=-{ \frac{1}{\,\sqrt{3}\,}}$$$${\small (3)}~\sin{(-3\pi)}=0$$$$~~~~~\cos{(-3\pi)}=-1$$$$~~~~~\tan{(-3\pi)}=0$$→ 三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
→ 【問題演習】三角関数の値(単位円)
p.118 問7$${\small (1)}~\sin{\left(-{ \frac{\,\pi\,}{6}}\right)}=-{ \frac{1}{\,2\,}}$$$$~~~~~\cos{\left(-{ \frac{\,\pi\,}{6}}\right)}={ \frac{\,\sqrt{3}\,}{2}}$$$$~~~~~\tan{\left(-{ \frac{\,\pi\,}{6}}\right)}=-{ \frac{1}{\,\sqrt{3}\,}}$$$${\small (2)}~\sin{\left(-{ \frac{2}{\,3\,}}\pi\right)}=-{ \frac{\,\sqrt{3}\,}{2}}$$$$~~~~~\cos{\left(-{ \frac{2}{\,3\,}}\pi\right)}=-{ \frac{1}{\,2\,}}$$$$~~~~~\tan{\left(-{ \frac{2}{\,3\,}}\pi\right)}=\sqrt{3}$$$${\small (3)}~\sin{\left(-{ \frac{\,5\,}{4}}\pi\right)}={ \frac{1}{\,\sqrt{2}\,}}$$$$~~~~~\cos{\left(-{ \frac{\,5\,}{4}}\pi\right)}=-{ \frac{1}{\,\sqrt{2}\,}}$$$$~~~~~\tan{\left(-{ \frac{\,5\,}{4}}\pi\right)}=-1$$
p.118 問8\({\small (1)}~\)第4象限
\({\small (2)}~\)第2象限
\({\small (3)}~\)第3象限
\({\small (2)}~\)第2象限
\({\small (3)}~\)第3象限
p.120 問9[証明]
\(\sin^2{\theta}+\cos^2{\theta}=1\) の両辺を \(\cos^2{\theta}\) で割ると、$$~~~{ \frac{\sin^2{\theta}}{\cos^2{\theta}}}+1={ \frac{1}{\cos^2{\theta}}}$$\({\large \frac{\sin{\theta}}{\cos{\theta}}}=\tan{\theta}\) より、$$~~~1+\tan^2{\theta}={ \frac{1}{\cos^2{\theta}}}$$[終]
\(\sin^2{\theta}+\cos^2{\theta}=1\) の両辺を \(\cos^2{\theta}\) で割ると、$$~~~{ \frac{\sin^2{\theta}}{\cos^2{\theta}}}+1={ \frac{1}{\cos^2{\theta}}}$$\({\large \frac{\sin{\theta}}{\cos{\theta}}}=\tan{\theta}\) より、$$~~~1+\tan^2{\theta}={ \frac{1}{\cos^2{\theta}}}$$[終]
p.121 問10$$~~~\cos{\theta}={ \frac{\,2\sqrt{2}\,}{3}}~,~\tan{\theta}=-{ \frac{\,\sqrt{2}\,}{4}}$$
p.121 問11$$~~~\cos{\theta}=-{ \frac{\,\sqrt{5}\,}{5}}~,~\sin{\theta}={ \frac{\,2\sqrt{5}\,}{5}}$$→ 三角関数の相互関係の公式
p.121 問12$$~~~\sin{\theta}\cos{\theta}={ \frac{12}{\,25\,}}$$$$~~~\sin^3{\theta}-\cos^3{\theta}={ \frac{37}{\,125\,}}$$→ 三角関数の式の値
p.121 問13\({\small (1)}~\)[証明]
(左辺)$$={ \frac{1}{\sin^2{\theta}}}\left({ \frac{1-\cos^2{\theta}}{\cos^2{\theta}}}\right)$$$$={ \frac{1}{\sin^2{\theta}}}\cdot{ \frac{\sin^2{\theta}}{\cos^2{\theta}}}$$$$={ \frac{1}{\cos^2{\theta}}}$$したがって、$$~{ \frac{1}{\sin^2{\theta}}}\left({ \frac{1}{\cos^2{\theta}}}-1\right)={ \frac{1}{\cos^2{\theta}}}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$={ \frac{\sin{\theta}}{\cos{\theta}}}+{ \frac{\cos{\theta}}{\sin{\theta}}}$$$$={ \frac{\sin^2{\theta}+\cos^2{\theta}}{\sin{\theta}\cos{\theta}}}$$$$={ \frac{1}{\sin{\theta}\cos{\theta}}}$$したがって、$$~\tan{\theta}+{ \frac{1}{\tan{\theta}}}={ \frac{1}{\sin{\theta}\cos{\theta}}}$$[終]
→ 三角関数の等式の証明
(左辺)$$={ \frac{1}{\sin^2{\theta}}}\left({ \frac{1-\cos^2{\theta}}{\cos^2{\theta}}}\right)$$$$={ \frac{1}{\sin^2{\theta}}}\cdot{ \frac{\sin^2{\theta}}{\cos^2{\theta}}}$$$$={ \frac{1}{\cos^2{\theta}}}$$したがって、$$~{ \frac{1}{\sin^2{\theta}}}\left({ \frac{1}{\cos^2{\theta}}}-1\right)={ \frac{1}{\cos^2{\theta}}}$$[終]
\({\small (2)}~\)[証明]
(左辺)$$={ \frac{\sin{\theta}}{\cos{\theta}}}+{ \frac{\cos{\theta}}{\sin{\theta}}}$$$$={ \frac{\sin^2{\theta}+\cos^2{\theta}}{\sin{\theta}\cos{\theta}}}$$$$={ \frac{1}{\sin{\theta}\cos{\theta}}}$$したがって、$$~\tan{\theta}+{ \frac{1}{\tan{\theta}}}={ \frac{1}{\sin{\theta}\cos{\theta}}}$$[終]
→ 三角関数の等式の証明
p.122 問14$$~~~\sin{{ \frac{\,27\,}{4}}\pi}={ \frac{1}{\,\sqrt{2}\,}}$$$$~~~\cos{{ \frac{\,27\,}{4}}\pi}=-{ \frac{1}{\,\sqrt{2}\,}}$$$$~~~\tan{{ \frac{\,27\,}{4}}\pi}=-1$$
p.122 問15$$~~~\sin{\left(-{ \frac{5}{\,6\,}}\pi\right)}=-{ \frac{1}{\,2\,}}$$$$~~~\cos{\left(-{ \frac{5}{\,6\,}}\pi\right)}=-{ \frac{\,\sqrt{3}\,}{2}}$$$$~~~\tan{\left(-{ \frac{5}{\,6\,}}\pi\right)}={ \frac{1}{\,\sqrt{3}\,}}$$
p.123 問16$${\small (1)}~a$$$${\small (2)}~-a$$$${\small (3)}~-a$$→ 三角関数の性質①
p.123 問17公式5
[証明]$$~~~~~\sin{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\sin{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=\cos{(-\theta)}=\cos{\theta}$$
$$~~~~~\cos{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\cos{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=-\sin{(-\theta)}=\sin{\theta}$$
$$~~~~~\tan{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\tan{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=-{ \frac{1}{\tan{(-\theta)}}}={ \frac{1}{\tan{\theta}}}$$[終]
公式6
[証明]
\(\sin{(\pi-\theta)}\)
\(=\sin{\{\pi+(-\theta)\}}\)
\(=-\sin{(-\theta)}=\sin{\theta}\)
\(\cos{(\pi-\theta)}\)
\(=\cos{\{\pi+(-\theta)\}}\)
\(=-\cos{(-\theta)}=-\cos{\theta}\)
\(\tan{(\pi-\theta)}\)
\(=\tan{\{\pi+(-\theta)\}}\)
\(=\tan{(-\theta)}=-\tan{\theta}\)
[終]
→ 三角関数の性質②
[証明]$$~~~~~\sin{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\sin{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=\cos{(-\theta)}=\cos{\theta}$$
$$~~~~~\cos{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\cos{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=-\sin{(-\theta)}=\sin{\theta}$$
$$~~~~~\tan{\left({ \frac{\pi}{2}}-\theta\right)}$$$$=\tan{\left\{{ \frac{\pi}{2}}+(-\theta)\right\}}$$$$=-{ \frac{1}{\tan{(-\theta)}}}={ \frac{1}{\tan{\theta}}}$$[終]
公式6
[証明]
\(\sin{(\pi-\theta)}\)
\(=\sin{\{\pi+(-\theta)\}}\)
\(=-\sin{(-\theta)}=\sin{\theta}\)
\(\cos{(\pi-\theta)}\)
\(=\cos{\{\pi+(-\theta)\}}\)
\(=-\cos{(-\theta)}=-\cos{\theta}\)
\(\tan{(\pi-\theta)}\)
\(=\tan{\{\pi+(-\theta)\}}\)
\(=\tan{(-\theta)}=-\tan{\theta}\)
[終]
→ 三角関数の性質②
p.127 問18 奇関数
p.130 問23\({\small (1)}~n\) を整数として、$$~~~\theta={ \frac{\,\pi\,}{3}}+2n\pi~,~{ \frac{2}{\,3\,}}\pi+2n\pi$$\({\small (2)}~n\) を整数として、$$~~~\theta={ \frac{\pi\,}{4}}+2n\pi~,~{ \frac{\,7\,}{4}}\pi+2n\pi$$
p.130 問24\({\small (1)}~n\) を整数として、$$~~~\theta={ \frac{\,\pi\,}{4}}+n\pi$$\({\small (2)}~n\) を整数として、$$~~~\theta={ \frac{5}{\,6\,}}\pi+n\pi$$→ 三角関数を含む方程式①
→ 【問題演習】三角関数を含む方程式
→ 【問題演習】三角関数を含む方程式
p.131 問25$${\small (1)}~\theta={ \frac{\,3\,}{2}}\pi~,~{ \frac{\,11\,}{6}}\pi$$$${\small (2)}~\theta={ \frac{7}{\,12\,}}\pi~,~{ \frac{\,23\,}{12}}\pi$$→ 三角関数を含む方程式②(範囲変化)
p.132 問26$${\small (1)}~{ \frac{\,\pi\,}{6}}<\theta<{ \frac{5}{\,6\,}}\pi$$$${\small (2)}~{ \frac{3}{\,4\,}}\pi≦\theta≦{ \frac{\,5\,}{4}}\pi$$$${\small (3)}~0≦\theta<{ \frac{\,\pi\,}{3}}~,~{ \frac{\,5\,}{3}}\pi<\theta<2\pi$$$${\small (4)}~0≦\theta≦{ \frac{\,5\,}{4}}\pi~,~{ \frac{\,7\,}{4}}\pi ≦ \theta<2\pi$$$${\small (5)}~0≦\theta≦{ \frac{\,\pi\,}{3}}~,~{ \frac{2}{\,3\,}}\pi ≦ \theta<2\pi$$
p.132 問27$$~~~0≦\theta≦\frac{\,\pi\,}{\,6\,}~,~\frac{\,\pi\,}{\,2\,}≦\theta < 2\pi$$
p.133 問28$${\small (1)}~{ \frac{\,\pi\,}{3}}<\theta<{ \frac{\,\pi\,}{2}}~,~{ \frac{\,4\,}{3}}\pi<\theta<{ \frac{\,3\,}{2}}\pi$$$${\small (2)}~{ \frac{\,\pi\,}{2}}<\theta≦{ \frac{5}{\,6\,}}\pi~,~{ \frac{\,3\,}{2}}\pi<\theta≦{ \frac{\,11\,}{6}}\pi$$→ 三角関数を含む不等式①
p.133 問29$$~~~-{ \frac{\,\pi\,}{3}}<\theta<{ \frac{\,\pi\,}{4}}$$
p.134 問30\(\theta={\large \frac{\\,pi\,}{3}}~,~{\large \frac{\,5\,}{3}}\pi\) で最大値 \({\large \frac{\,9\,}{4}}\)
\(\theta=\pi\) で最小値 \(0\)
→ 三角関数を含む2次関数
\(\theta=\pi\) で最小値 \(0\)
→ 三角関数を含む2次関数
p.135 問題 4\({\small (1)}~\)[証明]
(左辺)$$={ \frac{\sin{\theta}}{1+\cos{\theta}}}+{ \frac{\sin{\theta}}{1-\cos{\theta}}}$$$$={ \frac{\sin{\theta}(1-\cos{\theta})+\sin{\theta}(1+\cos{\theta})}{1-\cos^2{\theta}}}$$$$={ \frac{2\sin{\theta}}{\sin^2{\theta}}}$$$$={ \frac{2}{\sin{\theta}}}$$したがって、$${ \frac{\sin{\theta}}{1+\cos{\theta}}}+{ \frac{\sin{\theta}}{1-\cos{\theta}}}={ \frac{2}{\sin{\theta}}}$$[終]
\({\small (2)}~\)[証明]
\(\sin{\left({\large \frac{\pi}{2}}-\theta\right)}=\cos{\theta}\)
\(\cos{(\pi-\theta)}=-\cos{\theta}\)
また、$$~~~~~\sin{\left({ \frac{3}{2}\pi}+\theta\right)}$$$$=\sin{\left(\pi+{ \frac{\pi}{2}}+\theta\right)}$$$$=-\sin{\left({ \frac{\pi}{2}}+\theta\right)}$$$$=-\cos{\theta}$$これらより、
(左辺)
\(=\cos{\theta}+\cos{\theta}-\cos{\theta}-\cos{\theta}=0\)
したがって、$$~\cos{\theta}+\sin{\left({ \frac{\pi}{2}}-\theta\right)}$$$$~~~~+\cos{(\pi-\theta)}+\sin{\left({ \frac{3}{2}\pi}+\theta\right)}=0$$[終]
(左辺)$$={ \frac{\sin{\theta}}{1+\cos{\theta}}}+{ \frac{\sin{\theta}}{1-\cos{\theta}}}$$$$={ \frac{\sin{\theta}(1-\cos{\theta})+\sin{\theta}(1+\cos{\theta})}{1-\cos^2{\theta}}}$$$$={ \frac{2\sin{\theta}}{\sin^2{\theta}}}$$$$={ \frac{2}{\sin{\theta}}}$$したがって、$${ \frac{\sin{\theta}}{1+\cos{\theta}}}+{ \frac{\sin{\theta}}{1-\cos{\theta}}}={ \frac{2}{\sin{\theta}}}$$[終]
\({\small (2)}~\)[証明]
\(\sin{\left({\large \frac{\pi}{2}}-\theta\right)}=\cos{\theta}\)
\(\cos{(\pi-\theta)}=-\cos{\theta}\)
また、$$~~~~~\sin{\left({ \frac{3}{2}\pi}+\theta\right)}$$$$=\sin{\left(\pi+{ \frac{\pi}{2}}+\theta\right)}$$$$=-\sin{\left({ \frac{\pi}{2}}+\theta\right)}$$$$=-\cos{\theta}$$これらより、
(左辺)
\(=\cos{\theta}+\cos{\theta}-\cos{\theta}-\cos{\theta}=0\)
したがって、$$~\cos{\theta}+\sin{\left({ \frac{\pi}{2}}-\theta\right)}$$$$~~~~+\cos{(\pi-\theta)}+\sin{\left({ \frac{3}{2}\pi}+\theta\right)}=0$$[終]
p.135 問題 5\({\small (1)}~\)周期 \(\pi\)

\({\small (2)}~\)周期 \(4\pi\)

\({\small (3)}~\)周期 \({\large \frac{2}{\,3\,}}\pi\)

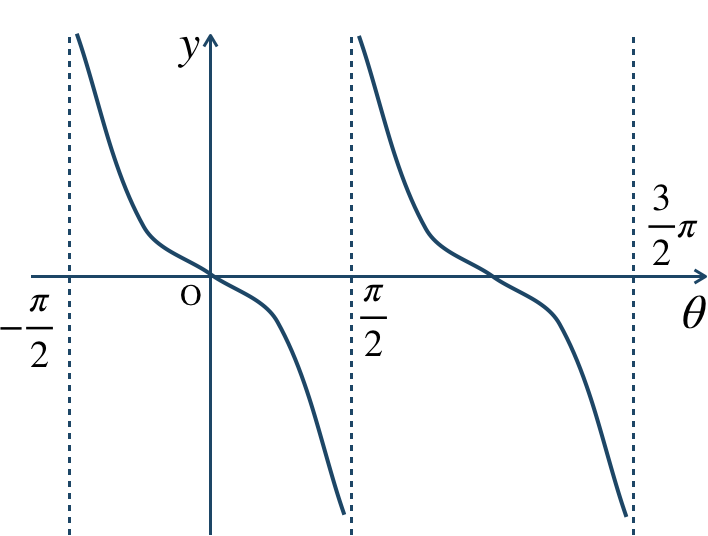
\({\small (2)}~\)周期 \(4\pi\)
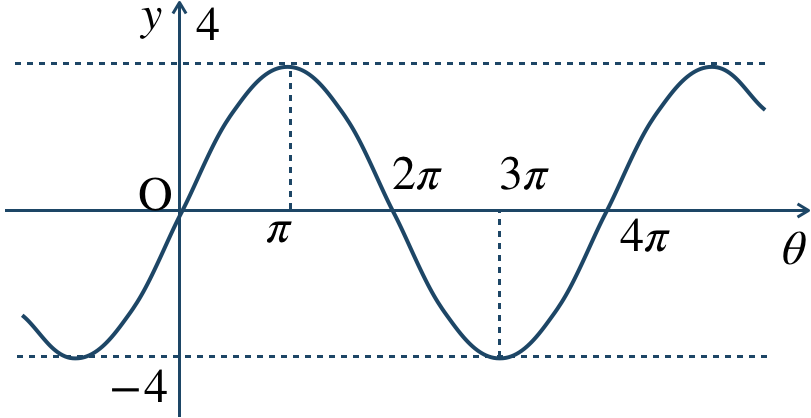
\({\small (3)}~\)周期 \({\large \frac{2}{\,3\,}}\pi\)

2節 加法定理
p.140 問1$$~~~{ \frac{\,\sqrt{6}-\sqrt{2}\,}{4}}~,~{ \frac{\,\sqrt{6}+\sqrt{2}\,}{4}}$$
p.140 問2$$~~~{ \frac{\,\sqrt{2}+\sqrt{6}\,}{4}}~,~{ \frac{\,\sqrt{2}-\sqrt{6}\,}{4}}$$→ 加法定理
p.140 問3$${\small (1)}~-{ \frac{77}{\,85\,}}$$$${\small (2)}~-{ \frac{84}{\,85\,}}$$$${\small (3)}~{ \frac{36}{\,85\,}}$$→ 加法定理と式の値
p.141 問4[証明]
\(\tan{(\alpha+\beta)}={\large \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}}\)
これより、\(\beta~\to~-\beta\) とすると、
\(\tan{(\alpha-\beta)}={\large \frac{\tan{\alpha}+\tan{(-\beta)}}{1-\tan{\alpha}\tan{(-\beta)}}}\)
ここで、\(\tan{(-\beta)}=-\tan{\beta}\) より、
\(\tan{(\alpha-\beta)}={\large \frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}}}\)
[終]
\(\tan{(\alpha+\beta)}={\large \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha}\tan{\beta}}}\)
これより、\(\beta~\to~-\beta\) とすると、
\(\tan{(\alpha-\beta)}={\large \frac{\tan{\alpha}+\tan{(-\beta)}}{1-\tan{\alpha}\tan{(-\beta)}}}\)
ここで、\(\tan{(-\beta)}=-\tan{\beta}\) より、
\(\tan{(\alpha-\beta)}={\large \frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}}}\)
[終]
p.141 問5$$~~~2-\sqrt{3}~,~-2-\sqrt{3}$$
p.141 問6$$~~~{ \frac{\,\pi\,}{4}}$$
p.142 問7$$~~~{ \frac{\,\pi\,}{4}}$$
p.142 問8$$~~~3$$→ 2直線のなす角
p.143 問9$$~~~\sin{2\alpha}=-{ \frac{\,4\sqrt{2}\,}{9}}~,~\cos{2\alpha}=-{ \frac{7}{\,9\,}}$$$$~~~\tan{2\alpha}={ \frac{\,4\sqrt{2}\,}{7}}$$→ 2倍角の公式
p.143 問10\({\small (1)}~\) [証明]
\(~~~~~\sin{3\alpha}\)
\(=\sin{(2\alpha+\alpha)}\)
\(=\sin{2\alpha}\cos{\alpha}+\cos{2\alpha}\sin{\alpha}\)
\(=2\sin{\alpha}\cos^2{\alpha}+(1-2\sin^2{\alpha})\sin{\alpha}\)
\(=2\sin{\alpha}(1-\sin^2{\alpha})+\sin{\alpha}-2\sin^3{\alpha}\)
\(=3\sin{\alpha}-4\sin^3{\alpha}\)
したがって、
\(\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}\) [終]
\({\small (2)}~\) [証明]
\(~~~~~\cos{3\alpha}\)
\(=\cos{(2\alpha+\alpha)}\)
\(=\cos{2\alpha}\cos{\alpha}-\sin{2\alpha}\sin{\alpha}\)
\(=(2\cos^2{\alpha}-1)\cos{\alpha}-2\sin^2{\alpha}\cos{\alpha}\)
\(=2\cos^3{\alpha}-\cos{\alpha}-2(1-\cos^2{\alpha})\cos{\alpha}\)
\(=4\cos^3{\alpha}-3\cos{\alpha}\)
したがって、
\(\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}\) [終]
\(~~~~~\sin{3\alpha}\)
\(=\sin{(2\alpha+\alpha)}\)
\(=\sin{2\alpha}\cos{\alpha}+\cos{2\alpha}\sin{\alpha}\)
\(=2\sin{\alpha}\cos^2{\alpha}+(1-2\sin^2{\alpha})\sin{\alpha}\)
\(=2\sin{\alpha}(1-\sin^2{\alpha})+\sin{\alpha}-2\sin^3{\alpha}\)
\(=3\sin{\alpha}-4\sin^3{\alpha}\)
したがって、
\(\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}\) [終]
\({\small (2)}~\) [証明]
\(~~~~~\cos{3\alpha}\)
\(=\cos{(2\alpha+\alpha)}\)
\(=\cos{2\alpha}\cos{\alpha}-\sin{2\alpha}\sin{\alpha}\)
\(=(2\cos^2{\alpha}-1)\cos{\alpha}-2\sin^2{\alpha}\cos{\alpha}\)
\(=2\cos^3{\alpha}-\cos{\alpha}-2(1-\cos^2{\alpha})\cos{\alpha}\)
\(=4\cos^3{\alpha}-3\cos{\alpha}\)
したがって、
\(\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}\) [終]
p.144 問11$${\small (1)}~\theta={ \frac{\,\pi\,}{3}}~,~{ \frac{\,\pi\,}{2}}~,~{ \frac{\,3\,}{2}}\pi~,~{ \frac{\,5\,}{3}}\pi$$$${\small (2)}~\theta={ \frac{\,\pi\,}{2}}~,~{ \frac{\,7\,}{6}}\pi~,~{ \frac{\,11\,}{6}}\pi$$
p.144 問12$$~~~\frac{\,\pi\,}{\,3\,}< \theta < \pi ~,~\pi < \theta <\frac{\,5\,}{\,3\,}\pi$$
p.145 問13[証明]
\(\tan{\alpha}={\large \frac{\sin{\alpha}}{\cos{\alpha}}}\) より、$$~~~~~\tan^2{{ \frac{\alpha}{2}}}$$$$={ \frac{\sin^2{{\large \frac{\alpha}{2}}}}{\cos^2{{\large \frac{\alpha}{2}}}}}$$$$={ \frac{{\large \frac{1-\cos{\alpha}}{2}}}{{\large \frac{1+\cos{\alpha}}{2}}}}$$$$={ \frac{1-\cos{\alpha}}{1+\cos{\alpha}}}$$したがって、$$~~~\tan^2{{ \frac{\alpha}{2}}}={ \frac{1-\cos{\alpha}}{1+\cos{\alpha}}}$$[終]
\(\tan{\alpha}={\large \frac{\sin{\alpha}}{\cos{\alpha}}}\) より、$$~~~~~\tan^2{{ \frac{\alpha}{2}}}$$$$={ \frac{\sin^2{{\large \frac{\alpha}{2}}}}{\cos^2{{\large \frac{\alpha}{2}}}}}$$$$={ \frac{{\large \frac{1-\cos{\alpha}}{2}}}{{\large \frac{1+\cos{\alpha}}{2}}}}$$$$={ \frac{1-\cos{\alpha}}{1+\cos{\alpha}}}$$したがって、$$~~~\tan^2{{ \frac{\alpha}{2}}}={ \frac{1-\cos{\alpha}}{1+\cos{\alpha}}}$$[終]
p.145 問14$$~~~{ \frac{\sqrt{\,2+\sqrt{2}\,}}{2}}~,~\sqrt{2}-1$$
p.145 問15$$~~~-{ \frac{\,\sqrt{6}\,}{6}}$$→ 半角の公式
p.147 問16$${\small (1)}~2\sin{\left(\theta+{ \frac{\,\pi\,}{6}}\right)}$$$${\small (2)}~\sqrt{2}\sin{\left(\theta-{ \frac{\,\pi\,}{4}}\right)}$$
p.147 問17$${\small (1)}~5\sin{(\theta+\alpha)}$$ただし、\(\alpha\) は、$$~~~\cos{\alpha}={ \frac{3}{\,5\,}}~,~\sin{\alpha}={ \frac{4}{\,5\,}}$$を満たす$${\small (2)}~\sqrt{29}\sin{(\theta+\alpha)}$$ただし、\(\alpha\) は、$$~~~\cos{\alpha}={ \frac{5}{\,\sqrt{29}\,}}~,~\sin{\alpha}=-{ \frac{2}{\,\sqrt{29}\,}}$$を満たす
→ 三角関数の合成
→ 三角関数の合成
p.148 問18\({\small (1)}~\)最大値 \(2\sqrt{3}\)、最小値 \(-2\sqrt{3}\)
\({\small (2)}~\)最大値 \(13\)、最小値 \(-13\)
→ 三角関数の最大値・最小値
\({\small (2)}~\)最大値 \(13\)、最小値 \(-13\)
→ 三角関数の最大値・最小値
p.149 問19$${\small (1)}~\theta={ \frac{\pi}{\,12\,}}~,~{ \frac{\,17\,}{12}}\pi$$$${\small (2)}~\theta=\pi~,~{ \frac{\,5\,}{3}}\pi$$→ 合成を用いる方程式と不等式
p.150 問題 11\({\small (1)}~\)[証明]
加法定理より、
(左辺)$$=\tan{\left({ \frac{\pi}{4}}+\theta\right)}$$$$={ \frac{\tan{{\large \frac{\pi}{4}}}+\tan{\theta}}{1-\tan{{\large \frac{\pi}{4}}}\tan{\theta}}}$$$$={ \frac{1+\tan{\theta}}{1-\tan{\theta}}}$$したがって、$$~~~\tan{\left({ \frac{\pi}{4}}+\theta\right)}={ \frac{1+\tan{\theta}}{1-\tan{\theta}}}$$[終]
\({\small (2)}~\)[証明]
2倍角の公式より、
(左辺)$$={ \frac{\sin{2\theta}}{1+\cos{2\theta}}}$$$$={ \frac{2\sin{\theta}\cos{\theta}}{1+(2\cos^2{\theta}-1)}}$$$$={ \frac{2\sin{\theta}\cos{\theta}}{2\cos^2{\theta}}}$$$$={ \frac{\sin{\theta}}{\cos{\theta}}}=\tan{\theta}$$したがって、$$~~~{ \frac{\sin{2\theta}}{1+\cos{2\theta}}}=\tan{\theta}$$[終]
加法定理より、
(左辺)$$=\tan{\left({ \frac{\pi}{4}}+\theta\right)}$$$$={ \frac{\tan{{\large \frac{\pi}{4}}}+\tan{\theta}}{1-\tan{{\large \frac{\pi}{4}}}\tan{\theta}}}$$$$={ \frac{1+\tan{\theta}}{1-\tan{\theta}}}$$したがって、$$~~~\tan{\left({ \frac{\pi}{4}}+\theta\right)}={ \frac{1+\tan{\theta}}{1-\tan{\theta}}}$$[終]
\({\small (2)}~\)[証明]
2倍角の公式より、
(左辺)$$={ \frac{\sin{2\theta}}{1+\cos{2\theta}}}$$$$={ \frac{2\sin{\theta}\cos{\theta}}{1+(2\cos^2{\theta}-1)}}$$$$={ \frac{2\sin{\theta}\cos{\theta}}{2\cos^2{\theta}}}$$$$={ \frac{\sin{\theta}}{\cos{\theta}}}=\tan{\theta}$$したがって、$$~~~{ \frac{\sin{2\theta}}{1+\cos{2\theta}}}=\tan{\theta}$$[終]
p.152 発展 問1[証明] 加法定理より、
\(\sin{(\alpha+\beta)}\)
\(=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}\) …①
\(\sin{(\alpha-\beta)}\)
\(=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\) …②
①−②より、
\(\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}\)
\(=2\cos{\alpha}\sin{\beta}\)
したがって、
\(\cos{\alpha}\sin{\beta}\)
\(={\large \frac{1}{2}}\left\{\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}\right\}\)
また、加法定理より、
\(\cos{(\alpha+\beta)}\)
\(=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}\) …③
\(\cos{(\alpha-\beta)}\)
\(=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}\) …④
③+④より、
\(\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\)
\(=2\cos{\alpha}\cos{\beta}\)
したがって、
\(\cos{\alpha}\cos{\beta}\)
\(={\large \frac{1}{2}}\left\{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\right\}\)
また、③−④より、
\(\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}\)
\(=-2\sin{\alpha}\sin{\beta}\)
したがって、
\(\sin{\alpha}\sin{\beta}\)
\(=-{\large \frac{1}{2}}\left\{\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}\right\}\)
[終]
\(\sin{(\alpha+\beta)}\)
\(=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}\) …①
\(\sin{(\alpha-\beta)}\)
\(=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\) …②
①−②より、
\(\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}\)
\(=2\cos{\alpha}\sin{\beta}\)
したがって、
\(\cos{\alpha}\sin{\beta}\)
\(={\large \frac{1}{2}}\left\{\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}\right\}\)
また、加法定理より、
\(\cos{(\alpha+\beta)}\)
\(=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}\) …③
\(\cos{(\alpha-\beta)}\)
\(=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}\) …④
③+④より、
\(\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\)
\(=2\cos{\alpha}\cos{\beta}\)
したがって、
\(\cos{\alpha}\cos{\beta}\)
\(={\large \frac{1}{2}}\left\{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\right\}\)
また、③−④より、
\(\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}\)
\(=-2\sin{\alpha}\sin{\beta}\)
したがって、
\(\sin{\alpha}\sin{\beta}\)
\(=-{\large \frac{1}{2}}\left\{\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}\right\}\)
[終]
p.152 発展 問2$${\small (1)}~{ \frac{\,\sqrt{2}\,}{4}}$$$${\small (2)}~{ \frac{\,\sqrt{2}\,}{4}}$$
p.152 発展 問3$${\small (1)}~{ \frac{1}{\,2\,}}(\sin{4\theta}-\sin{2\theta})$$$${\small (2)}~{ \frac{1}{\,2\,}}(\cos{5\theta}+\cos{\theta})$$$${\small (3)}~-{ \frac{1}{\,2\,}}(\cos{5\theta}-\cos{3\theta})$$
p.153 発展 問4$${\small (1)}~{ \frac{\,\sqrt{2}\,}{2}}$$$${\small (2)}~{ \frac{\,\sqrt{6}\,}{2}}$$
p.153 発展 問5$${\small (1)}~2\sin{4\theta}\cos{\theta}$$$${\small (2)}~2\sin{3\theta}\sin{\theta}$$
p.153 発展 問6$$~~~\theta=0~,~{ \frac{\,\pi\,}{2}}~,~\pi~,~{ \frac{\,3\,}{2}}\pi$$
練習問題 三角関数
p.154 練習問題A 3[証明]
(左辺)$$={ \frac{1+\cos{\theta}}{1-\sin{\theta}}}-{ \frac{1-\cos{\theta}}{1+\sin{\theta}}}$$$$={\scriptsize \frac{(1+\cos{\theta})(1+\sin{\theta})-(1-\cos{\theta})(1-\sin{\theta})}{(1-\sin{\theta})(1+\sin{\theta})}}$$$$={ \frac{2\cos{\theta}+2\sin{\theta}}{1-\sin^2{\theta}}}$$$$={ \frac{2\cos{\theta}+2\sin{\theta}}{\cos^2{\theta}}}$$$$={ \frac{2+2{\large \frac{\sin{\theta}}{\cos{\theta}}}}{\cos{\theta}}}$$$$={ \frac{2(1+\tan{\theta})}{\cos{\theta}}}$$したがって、$$~~{ \frac{1+\cos{\theta}}{1-\sin{\theta}}}-{ \frac{1-\cos{\theta}}{1+\sin{\theta}}}$$$$~~~~~~={ \frac{2(1+\tan{\theta})}{\cos{\theta}}}$$[終]
(左辺)$$={ \frac{1+\cos{\theta}}{1-\sin{\theta}}}-{ \frac{1-\cos{\theta}}{1+\sin{\theta}}}$$$$={\scriptsize \frac{(1+\cos{\theta})(1+\sin{\theta})-(1-\cos{\theta})(1-\sin{\theta})}{(1-\sin{\theta})(1+\sin{\theta})}}$$$$={ \frac{2\cos{\theta}+2\sin{\theta}}{1-\sin^2{\theta}}}$$$$={ \frac{2\cos{\theta}+2\sin{\theta}}{\cos^2{\theta}}}$$$$={ \frac{2+2{\large \frac{\sin{\theta}}{\cos{\theta}}}}{\cos{\theta}}}$$$$={ \frac{2(1+\tan{\theta})}{\cos{\theta}}}$$したがって、$$~~{ \frac{1+\cos{\theta}}{1-\sin{\theta}}}-{ \frac{1-\cos{\theta}}{1+\sin{\theta}}}$$$$~~~~~~={ \frac{2(1+\tan{\theta})}{\cos{\theta}}}$$[終]
p.154 練習問題A 5$${\small (1)}~y={ \frac{1}{\,2\,}}\sin{2\theta}$$
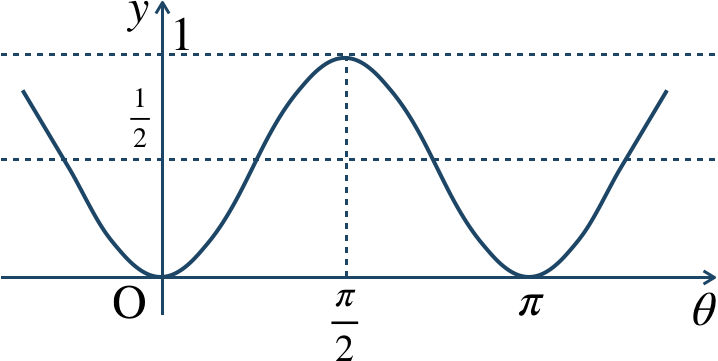
$${\small (2)}~y=-{ \frac{1}{\,2\,}}\cos{2\theta}+{ \frac{1}{\,2\,}}$$
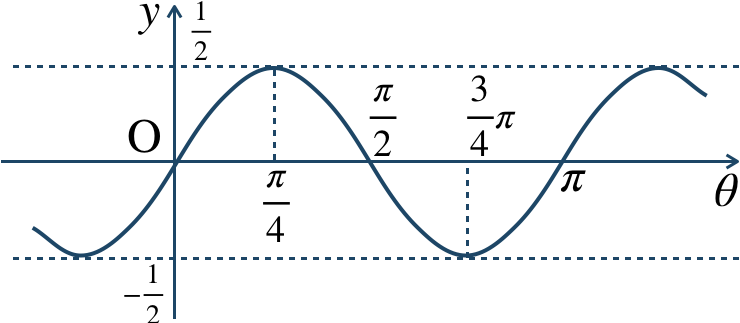
$${\small (2)}~y=-{ \frac{1}{\,2\,}}\cos{2\theta}+{ \frac{1}{\,2\,}}$$
p.154 練習問題A 6\({\small (1)}~\)[証明]
\(2\theta=36^\circ~,~3\theta=54^\circ\)
これより、
\(\sin{2\theta}\)
\(=\sin{36^\circ}=\sin{(90^\circ-54^\circ)}\)
\(=\cos{54^\circ}\)
\(=\cos{3\theta}\)
したがって、
\(\sin{2\theta}=\cos{3\theta}\) [終]
$${\small (2)}~{ \frac{\,-1+\sqrt{5}\,}{4}}$$
\(2\theta=36^\circ~,~3\theta=54^\circ\)
これより、
\(\sin{2\theta}\)
\(=\sin{36^\circ}=\sin{(90^\circ-54^\circ)}\)
\(=\cos{54^\circ}\)
\(=\cos{3\theta}\)
したがって、
\(\sin{2\theta}=\cos{3\theta}\) [終]
$${\small (2)}~{ \frac{\,-1+\sqrt{5}\,}{4}}$$
p.155 練習問題B 13\({\small (1)}~\)[証明]
\(\triangle {\rm ABQ}\) において、
\(\cos{\theta}={\large \frac{{\rm AQ}}{{\rm AB}}}~\Leftrightarrow~{\rm AQ}=\cos{\theta}\)
\(\triangle {\rm DAP}\) において、
\(\sin{\theta}={\large \frac{{\rm AP}}{{\rm AD}}}~\Leftrightarrow~{\rm AP}=\sin{\theta}\)
よって、1辺の長さ \({\rm PQ}\) は、
\({\rm PQ=AQ-AP}=\cos{\theta}-\sin{\theta}\)
[終]
$${\small (2)}~{ \frac{\pi}{\,12\,}}$$
\(\triangle {\rm ABQ}\) において、
\(\cos{\theta}={\large \frac{{\rm AQ}}{{\rm AB}}}~\Leftrightarrow~{\rm AQ}=\cos{\theta}\)
\(\triangle {\rm DAP}\) において、
\(\sin{\theta}={\large \frac{{\rm AP}}{{\rm AD}}}~\Leftrightarrow~{\rm AP}=\sin{\theta}\)
よって、1辺の長さ \({\rm PQ}\) は、
\({\rm PQ=AQ-AP}=\cos{\theta}-\sin{\theta}\)
[終]
$${\small (2)}~{ \frac{\pi}{\,12\,}}$$
次のページ「4章 指数関数・対数関数」