このページは、東京書籍:Standard数学Ⅱ[702]
2章 図形と方程式
2章 図形と方程式

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Standard数学Ⅱ 1章 方程式・式と証明
Standard数学Ⅱ 2章 図形と方程式
Standard数学Ⅱ 3章 三角関数
Standard数学Ⅱ 4章 指数関数・対数関数
Standard数学Ⅱ 5章 微分と積分
2章 図形と方程式
1節 点と直線
p.70 問1 A:第4象限
B:第2象限
C:第3象限
D:第1象限
B:第2象限
C:第3象限
D:第1象限
p.71 問2$${\small (1)}~\sqrt{10}$$$${\small (2)}~5$$$${\small (3)}~2\sqrt{5}$$$${\small (4)}~7$$→ 平面上の線分の長さ
p.73 問3
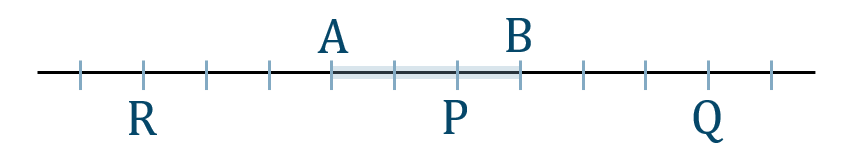
p.74 問4$${\small (1)}~{\rm P}(5)$$$${\small (2)}~{\rm Q}(-3)$$$${\small (3)}~{\rm M}\left( \frac{\,9\,}{\,2\,} \right)$$→ 直線上の線分の長さ・内分点・外分点
p.77 問5\({\small (1)}~\)$${\rm P}(6~,~5)~,~{\rm Q}(30~,~29)~,~{\rm M}\left({ \frac{\,11\,}{2}}~,~{ \frac{\,9\,}{2}}\right)$$\({\small (2)}~\)$${\rm P}\left({ \frac{\,18\,}{7}}~,~{ \frac{5}{\,7\,}}\right)~,~{\rm Q}(30~,~-13)~,~{\rm M}(2~,~1)$$→ 平面上の内分点・外分点・重心
p.77 問6$$~~~(-10~,~-1)$$→ 点に対して対称な点
p.78 問7$${\small (1)}~(1~,~2)$$$${\small (2)}~\left({ \frac{\,7\,}{3}}~,~-{ \frac{\,5\,}{3}}\right)$$→ 平面上の内分点・外分点・重心
p.80 問8$${\small (1)}~y=2x+1$$$${\small (2)}~y=-{ \frac{1}{\,3\,}}x+3$$→ 直線の方程式
p.80 問9$${\small (1)}~y=2x+7$$$${\small (2)}~y=-3x+6$$$${\small (3)}~x=-4$$$${\small (4)}~y=5$$→ 2点を通る直線の方程式
p.81 問10$$~~~2x+y-4=0$$
p.83 問11 互いに平行:②と③
互いに垂直:①と④
互いに垂直:①と④
p.84 問13$$~~~(-2~,~2)$$→ 直線に対して対称な点
p.86 問14$${\small (1)}~{ \frac{\,2\sqrt{5}\,}{5}}$$$${\small (2)}~1$$→ 点と直線との距離
p.87 問15\({\rm A}(a~,~b)~,~{\rm B}(c~,~d)~,~{\rm C}(e~,~f)\) とすると、文字が6つとなり計算が難しくなる
説明のように、\({\rm A}(a~,~b)~,~{\rm B}(-c~,~0)~,~{\rm C}(c~,~0)\) とすると、文字が3つとなり計算が楽になる
説明のように、\({\rm A}(a~,~b)~,~{\rm B}(-c~,~0)~,~{\rm C}(c~,~0)\) とすると、文字が3つとなり計算が楽になる
p.88 参考 問1$$~~~16x-7y-9=0$$→ 2直線の交点を通る直線
Training
p.89 Training 1$${\small (1)}~9\sqrt{2}$$$${\small (2)}~4\sqrt{5}$$
p.89 Training 2$$~~~{\rm P}\left(-1~,~{ \frac{\,10\,}{7}}\right)~,~{\rm Q}\left(-{ \frac{\,23\,}{3}}~,~-10\right)$$
p.89 Training 3$$~~~(-4~,~-1)$$
p.89 Training 4$$~~~(1~,~3)$$
p.89 Training 5$${\small (1)}~y=-{ \frac{2}{\,3\,}}x+3$$$${\small (2)}~x=-2$$
p.89 Training 6$$~~~x+2y=0$$
p.89 Training 7 平行 \(3x-2y-1=0\)
垂直 \(2x+3y-18=0\)
垂直 \(2x+3y-18=0\)
p.89 Training 8$$~~~(0~,~1)$$
p.89 Training 9$${\small (1)}~{ \frac{\,5\sqrt{10}\,}{4}}$$$${\small (2)}~2\sqrt{2}$$
p.89 Training 10この2直線は、$$~~~y=-x+1~,~y=-x+\frac{\,5\,}{\,2\,}$$となり、傾きが等しく平行であり、切片が異なるので一致はしない
したがって、この2直線は交点をもたないので連立方程式の解をもたない
したがって、この2直線は交点をもたないので連立方程式の解をもたない
2節 円
p.90 問1$${\small (1)}~(x-2)^2+(y+1)^2=9$$$${\small (2)}~x^2+y^2=4$$
p.91 問2$$~~~(x-2)^2+(y-3)^2=45$$→ 円の方程式
p.91 問3$$~~~(x+1)^2+(y-2)^2=13$$→ 円の方程式の決定①(点の条件)
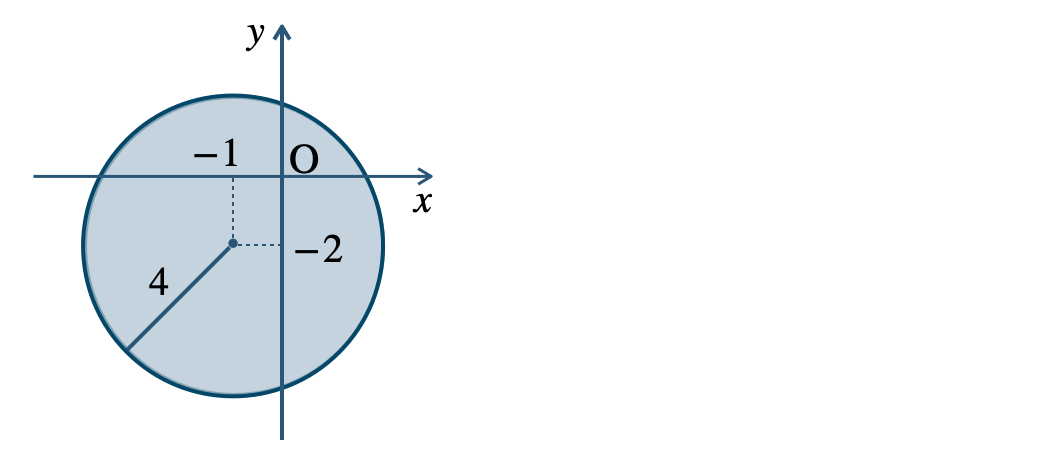
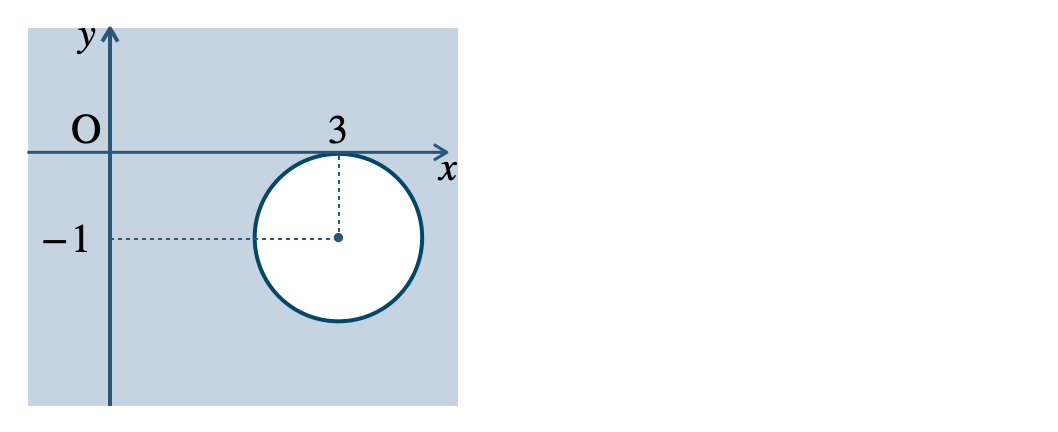
p.92 問4\({\small (1)}~\)中心 \((3~,~-2)\)、半径 \(3\) の円
\({\small (2)}~\)中心 \((-1~,~0)\)、半径 \(1\) の円
\({\small (3)}~\)点 \((-2~,~5)\)
→ 円の方程式
\({\small (2)}~\)中心 \((-1~,~0)\)、半径 \(1\) の円
\({\small (3)}~\)点 \((-2~,~5)\)
→ 円の方程式
p.93 問5$$~~~x^2+y^2-4x-6=0$$→ 円の方程式の決定①(点の条件)
p.94 問6$${\small (1)}~(-3~,~-4)~,~(4~,~3)$$$${\small (2)}~(2~,~2)$$→ 円と直線との共有点
p.95 問7$$~~~k<-5\sqrt{2}~,~5\sqrt{2}<k$$
p.96 問8$$~~~k=\pm3\sqrt{2}$$→ 円と直線との位置関係
p.96 問9連立すると、$$\begin{eqnarray}~~~x^2+(2x+k)^2&=&1\\[2pt]~~~5x^2+4kx+k^2-1&=&0\end{eqnarray}$$判別式を \(D\) とすると、$$~~~\frac{\,D\,}{\,4\,}=4k^2-5(k^2-1)=-k^2+5$$接するので \(D=0\) より、$$\begin{eqnarray}~~~-k^2+5&=&0\\[2pt]~~~k&=&\pm \sqrt{5}\end{eqnarray}$$
p.97 問10$${\small (1)}~3x+y=10$$$$({\small (2)}~2x-3y=-13$$$${\small (3)}~x=3$$
p.98 問11$$~~~3x+y=10~,~x-3y=-10$$→ 円の接線の方程式
p.99 問12$$~~~(x-2)^2+(y+2)^2=2$$→ 2つの円の位置関係
p.100 問13$$~~~(1~,~-2)~,~(2~,~1)$$
p.101 参考 問1$${\small (1)}~x^2+y^2-x+{ \frac{1}{\,3\,}}y-{ \frac{\,10\,}{3}}=0$$$${\small (2)}~3x-y-2=0$$→ 2つの円の交点を通る円・直線
Training
p.102 Training 11$${\small (1)}~(x+4)^2+(y-3)^2=9$$$${\small (2)}~x^2+(y-2)^2=5$$
p.102 Training 12\({\small (1)}~\)中心 \((-2~,~5)\)、半径 \(6\)
\({\small (2)}~\)中心 \(\left(0~,~-{\large \frac{5}{2}}\right)\)、半径 \({\large \frac{\sqrt{17}}{2}}\)
\({\small (3)}~\)点 \((2~,~3)\)
\({\small (2)}~\)中心 \(\left(0~,~-{\large \frac{5}{2}}\right)\)、半径 \({\large \frac{\sqrt{17}}{2}}\)
\({\small (3)}~\)点 \((2~,~3)\)
p.102 Training 13$$~~~x^2+y^2-8x-8y+12=0$$ 中心 \((4,4)\)、半径 \(2\sqrt{5}\)
p.102 Training 14$${\small (1)}~(-2~,~3)~,~(3~,~-2)$$$${\small (2)}~(-2~,~1)$$
p.102 Training 15\(-3\sqrt{10}<k<3\sqrt{10}\) のとき、
共有点2個
\(k=\pm3\sqrt{10}\) のとき、
共有点1個
\(k<-3\sqrt{10}~,~3\sqrt{10}<k\) のとき、
共有点0個
共有点2個
\(k=\pm3\sqrt{10}\) のとき、
共有点1個
\(k<-3\sqrt{10}~,~3\sqrt{10}<k\) のとき、
共有点0個
p.102 Training 16$${\small (1)}~x-3y=-10$$$${\small (2)}~y=4$$
p.102 Training 17$$~~~x+7y=50~,~x-y=10$$
p.102 Training 18$${\small (1)}~r=4$$$${\small (2)}~4<r<6$$
p.102 Training 19\((x-a)^2+(y-b)^2=k\) と式変形して、\(k>0\) であればよい
3節 軌跡と領域
p.104 問1直線 \(3x-5y+8=0\)
p.104 問2中心が原点、半径 \(4\) の円
p.105 問4直線 \(y=2x-3\)
p.107 問6\({\small (1)}~\)境界線を含まない




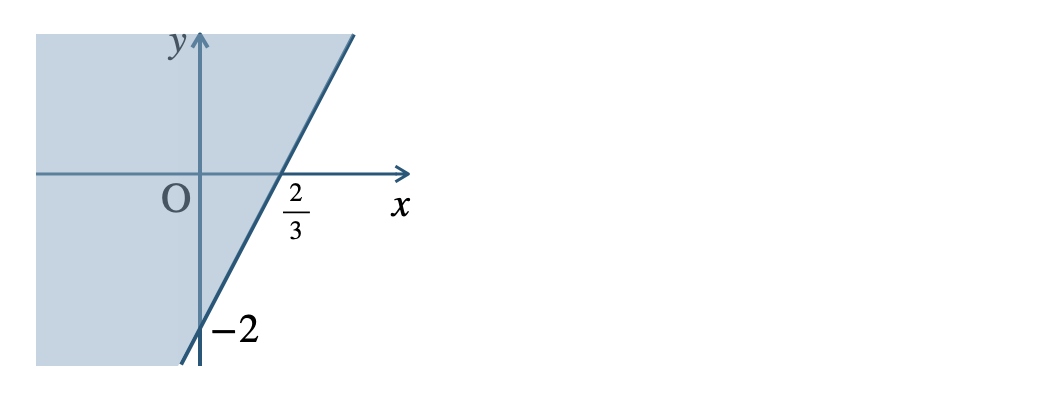
\({\small (2)}~\)境界線を含まない
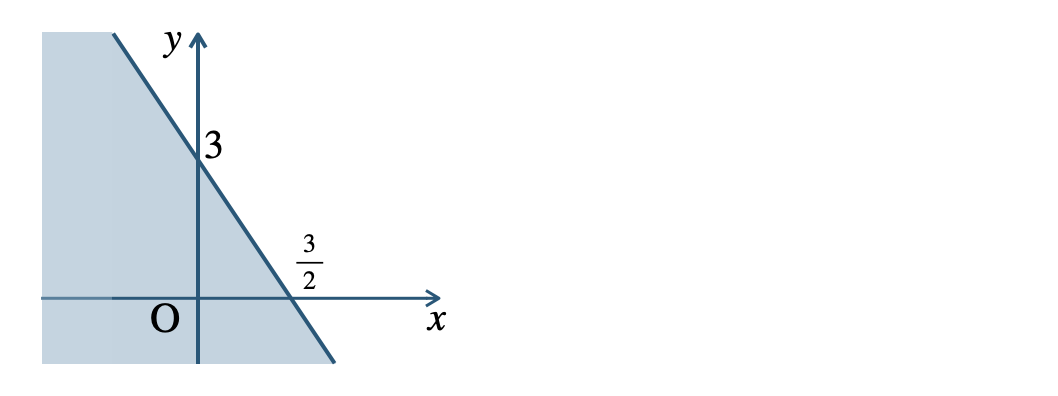
\({\small (3)}~\)境界線を含む
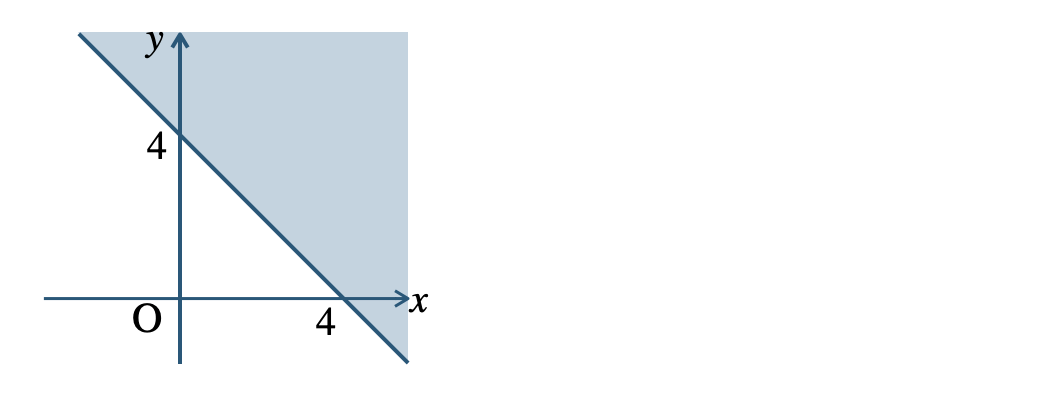
\({\small (4)}~\)境界線を含む
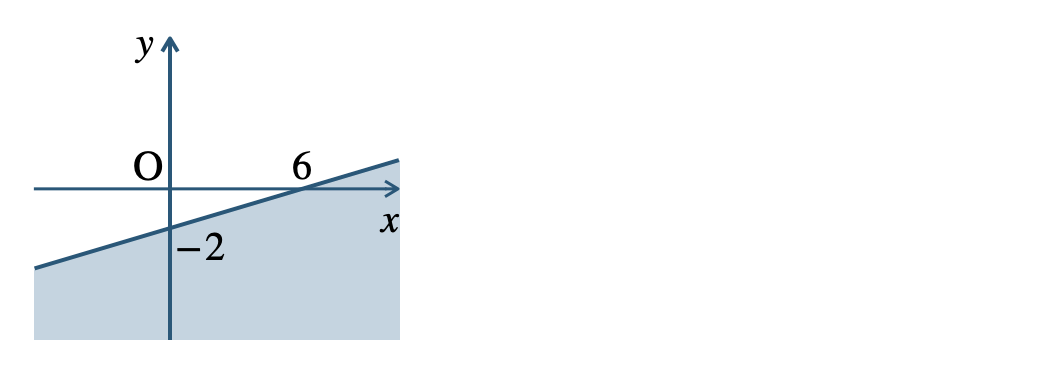
p.107 問7\({\small (1)}~\)境界線を含まない


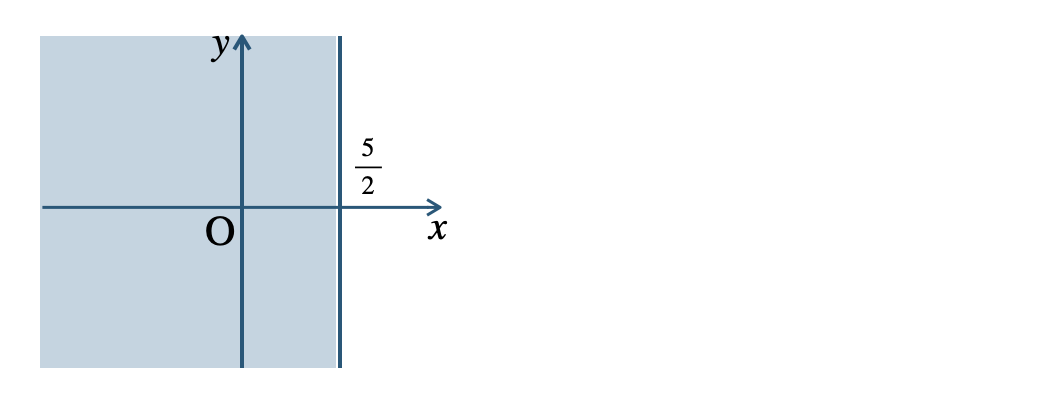
\({\small (2)}~\)境界線を含む
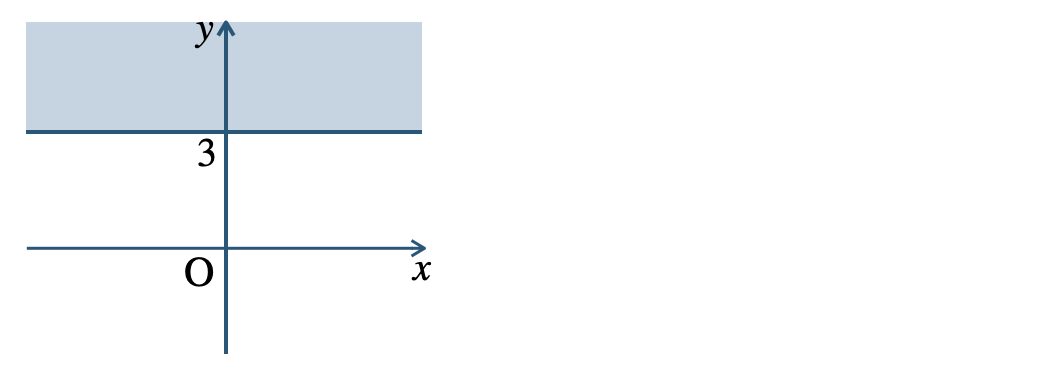
p.108 問8\({\small (1)}~\)境界線を含まない


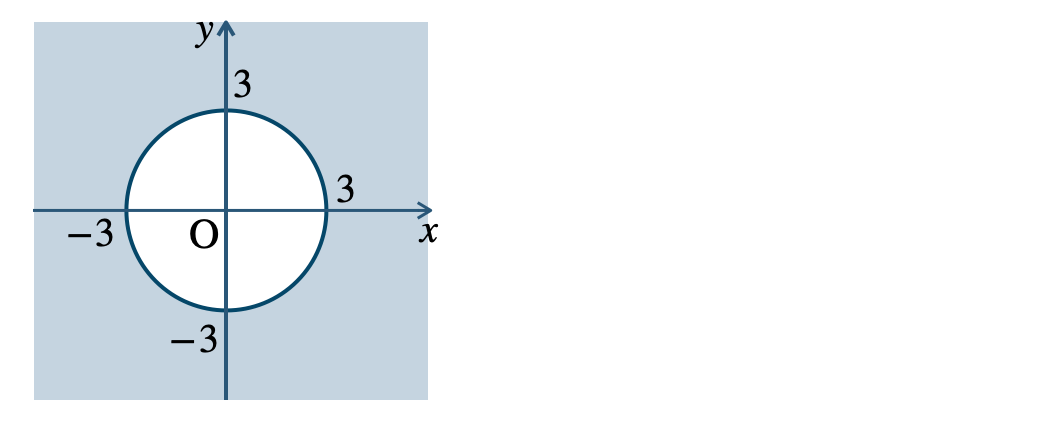
\({\small (2)}~\)境界線を含む
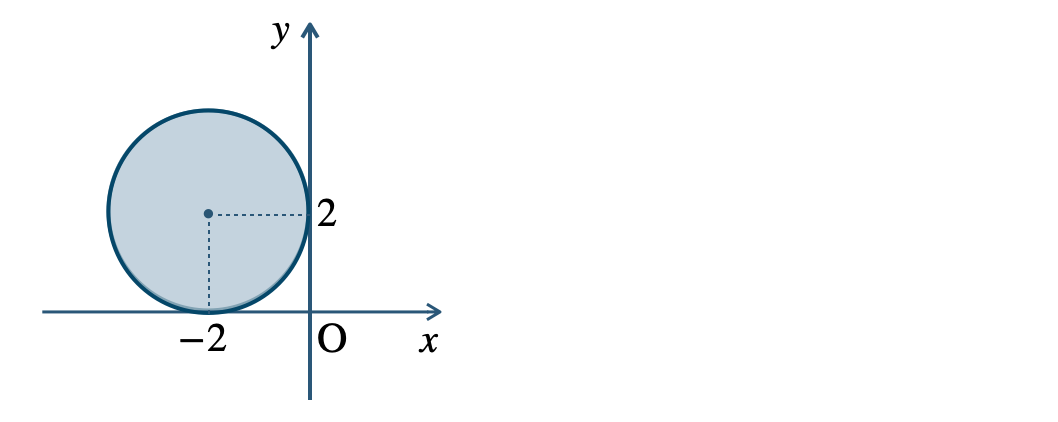
p.109 問10\({\small (1)}~\)境界線を含まない


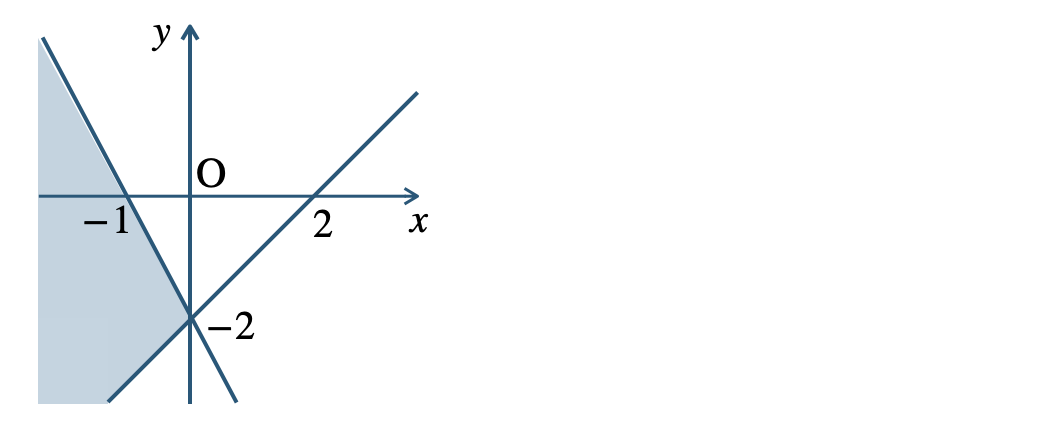
\({\small (2)}~\)境界線を含む
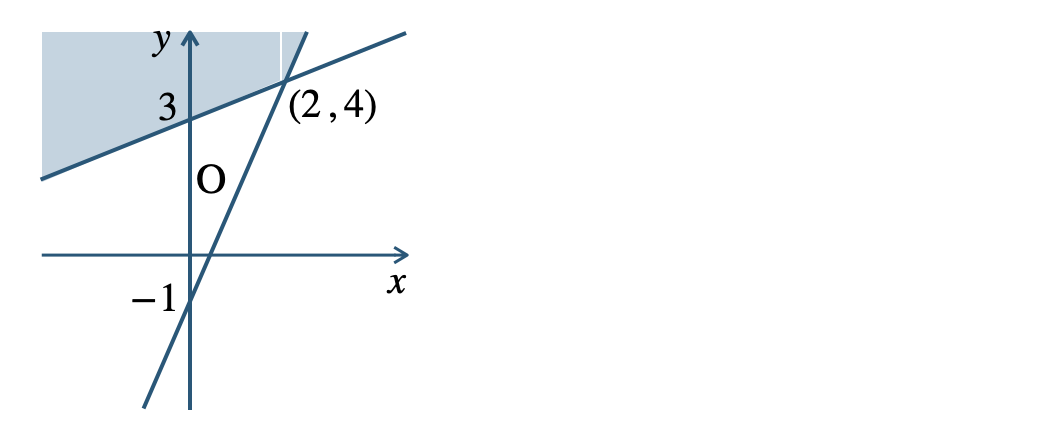
p.109 問11第1象限$$\begin{eqnarray} \left\{\begin{array}{l}
x > 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第2象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第3象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$第4象限$$\begin{eqnarray} \left\{\begin{array}{l}
x > 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$
x > 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第2象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第3象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$第4象限$$\begin{eqnarray} \left\{\begin{array}{l}
x > 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$
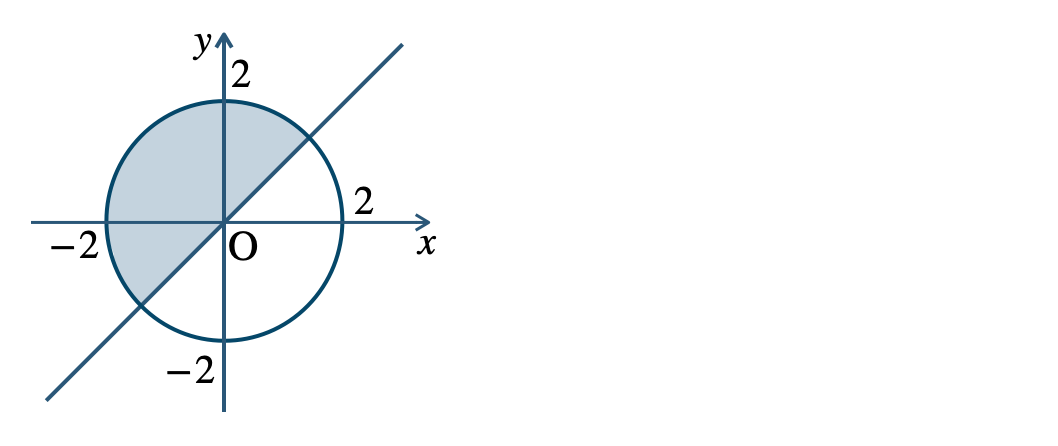
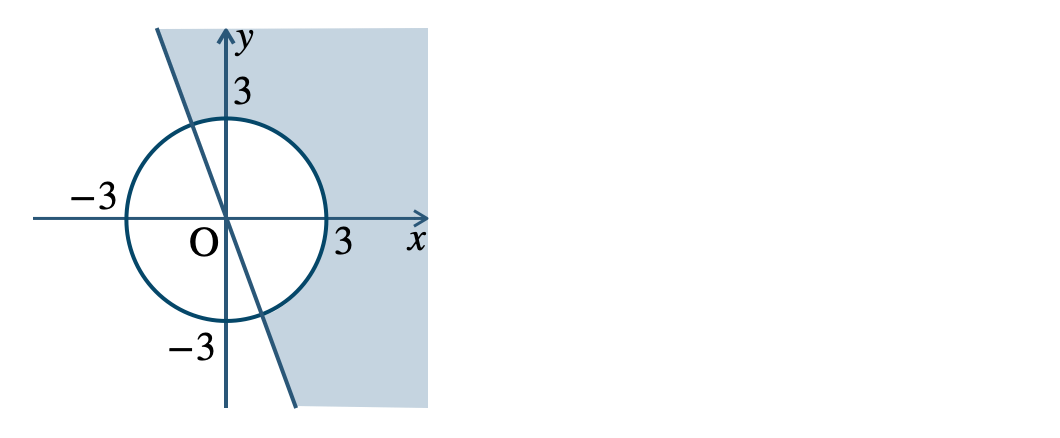
p.112 challenge 問1[証明] \(x^2+y^2<2\) の領域を \(P\)、\(x+y<2\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる
これらの領域を図示すると次の図のようになる
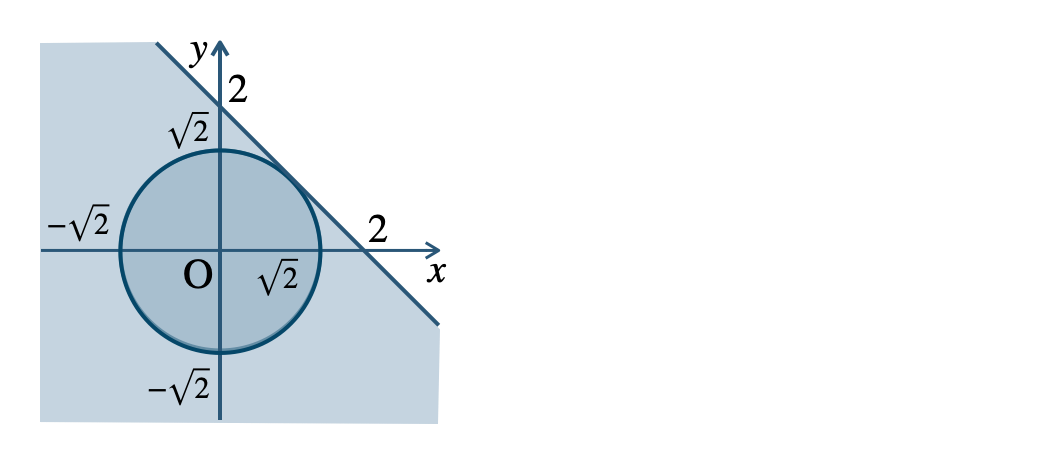
これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2<2\) ならば \(x+y<2\)
[終]
→ 領域を用いた証明
Training
p.113 Training 20直線 \(x=2\)
p.113 Training 21中心が\((-3~,~0)\)、半径 \(3\) の円
p.113 Training 22\({\small (1)}~\)
中心が\(\left({\large \frac{\,5\,}{2}}~,~1\right)\)、半径 \(\sqrt{3}\) の円
\({\small (2)}~\)直線 \(x-2y+2=0\)
中心が\(\left({\large \frac{\,5\,}{2}}~,~1\right)\)、半径 \(\sqrt{3}\) の円
\({\small (2)}~\)直線 \(x-2y+2=0\)
p.113 Training 23\({\small (1)}~\)境界線を含まない



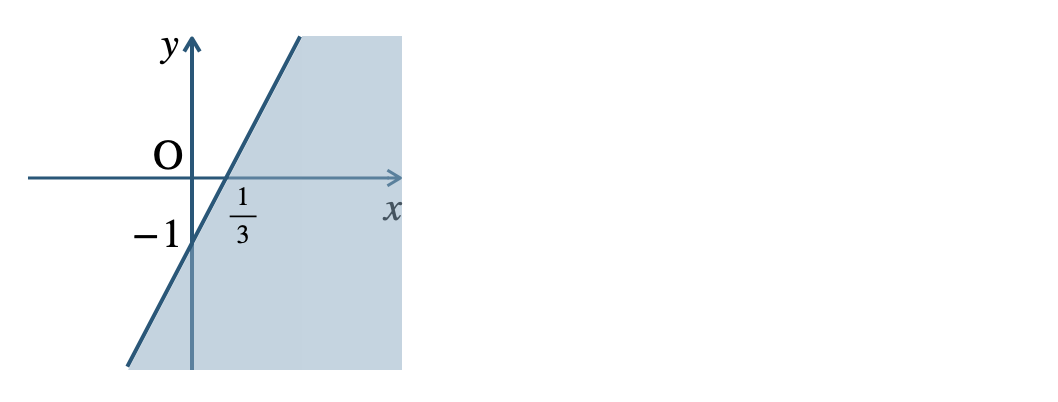
\({\small (2)}~\)境界線を含む
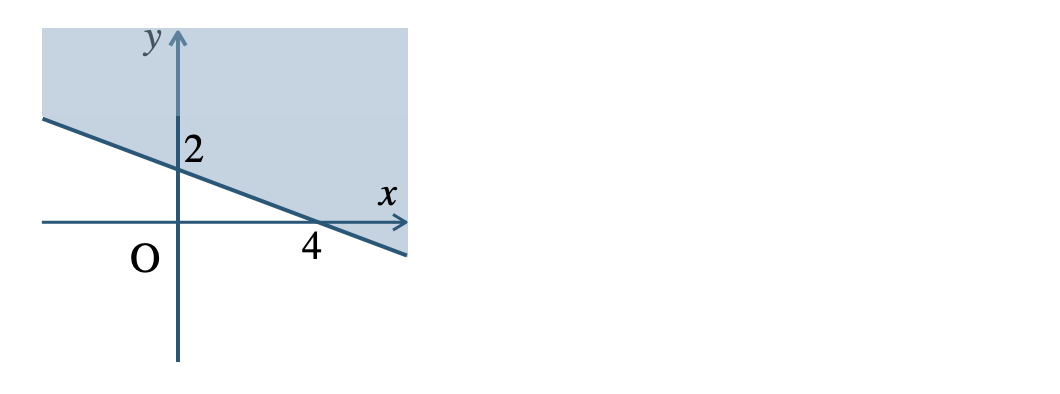
\({\small (3)}~\)境界線を含まない
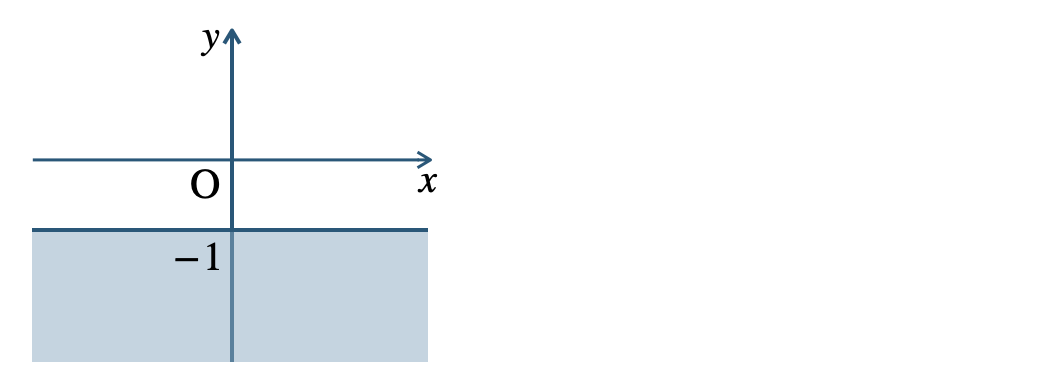
p.113 Training 24\({\small (1)}~\)境界線を含まない



\({\small (2)}~\)境界線を含む

p.113 Training 25\({\small (1)}~\)境界線を含む


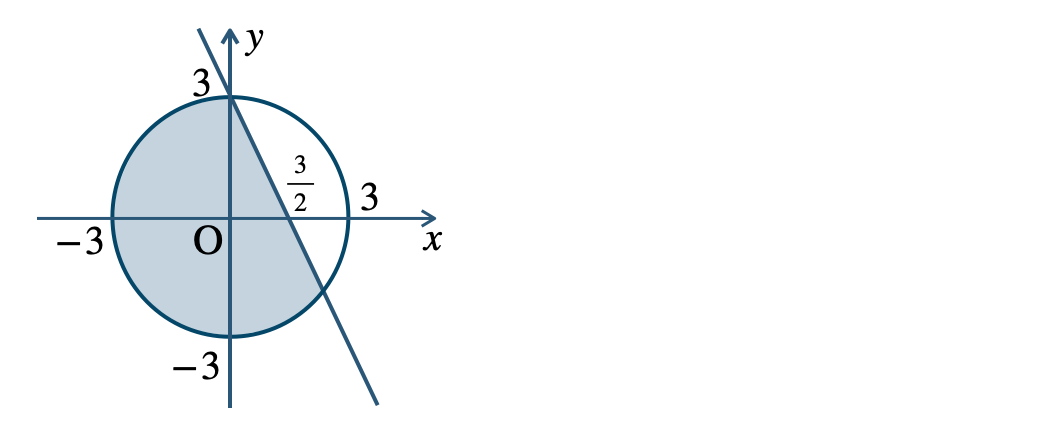
\({\small (2)}~\)境界線を含まない
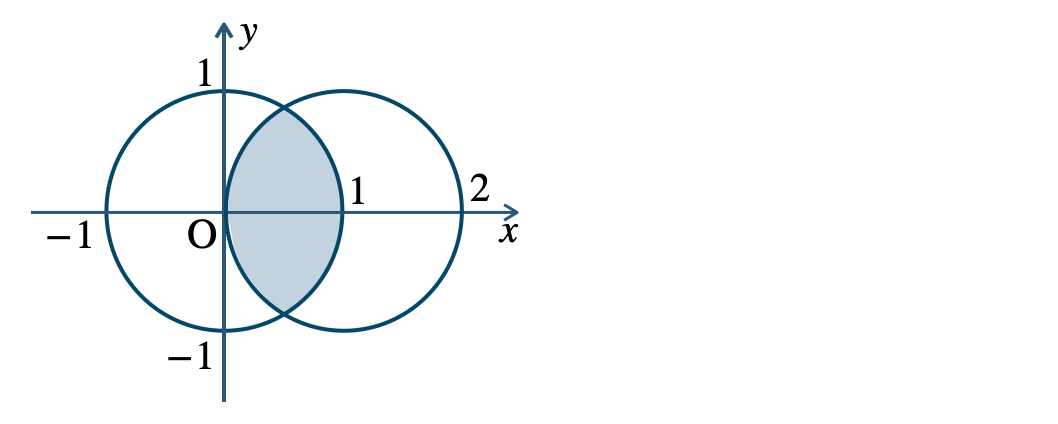
p.113 Training 26最大値 \(2~(x=2~,~y=4)\)
最小値 \(-4~(x=5~,~y=1)\)
最小値 \(-4~(x=5~,~y=1)\)
p.113 Training 27(イ) ②、(ウ) ③
Level Up 図形と方程式
p.114 Level Up 1$$~~~(3~,~0)$$
p.114 Level Up 2$$~~~(-3~,~1)$$→ 平行四辺形を作る点の座標
p.114 Level Up 3$$~~~a=1$$
p.114 Level Up 4\({\small (1)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が平行となるので、
\(-{\large \frac{a}{b}}=-{\large \frac{a’}{b’}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
\({\small (2)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が垂直となるので、
\(\left(-{\large \frac{a}{b}}\right)\left(-{\large \frac{a’}{b’}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が平行となるので、
\(-{\large \frac{a}{b}}=-{\large \frac{a’}{b’}}\)
式変形すると、
\(ab’-a’b=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~ab’-a’b=0\)
\({\small (2)}~\)
それぞれの直線の傾きは、
\(-{\large \frac{a}{b}}~,~-{\large \frac{a’}{b’}}\)
これより、2直線が垂直となるので、
\(\left(-{\large \frac{a}{b}}\right)\left(-{\large \frac{a’}{b’}}\right)=-1\)
式変形すると、
\(aa’+bb’=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~aa’+bb’=0\)
p.114 Level Up 5$$~~~2x-y-4=0$$→ 垂直二等分線の方程式
p.114 Level Up 6$${\small (1)}~5$$$${\small (2)}~{ \frac{\,22\,}{5}}$$$${\small (3)}~11$$
p.114 Level Up 7$${\small (1)}~(x-3)^2+(y-2)^2=5$$$${\small (2)}~(x-1)^2+(y-1)^2=1$$ または$$~~~~~~(x-5)^2+(y-5)^2=25$$
p.115 Level Up 8$$~~~m<-\sqrt{15}~,~\sqrt{15}<m$$
p.115 Level Up 9$$~~~\sqrt{6}$$→ 円によって切り取られる線分
p.115 Level Up 10$$~~~y=x~,~y=-x$$
p.115 Level Up 11中心が\((1~,~2)\)、半径 \(3\) の円
p.115 Level Up 12中心が\((4~,~0)\)、半径 \(1\) の円
p.115 Level Up 13$${\small (1)}~\begin{eqnarray} \left\{\begin{array}{l}
y<x+1\\y>4x-8 \\y>-{ \frac{1}{\,2\,}}x+1
\end{array}\right.\end{eqnarray}$$$${\small (2)}~\begin{eqnarray} \left\{\begin{array}{l}
x^2+y^2>1\\(x-1)^2+y^2<4
\end{array}\right.\end{eqnarray}$$
y<x+1\\y>4x-8 \\y>-{ \frac{1}{\,2\,}}x+1
\end{array}\right.\end{eqnarray}$$$${\small (2)}~\begin{eqnarray} \left\{\begin{array}{l}
x^2+y^2>1\\(x-1)^2+y^2<4
\end{array}\right.\end{eqnarray}$$
p.115 Level Up 14最大値 \(11~(x=4~,~y=-3)\)
最小値 \(-5~(x=-2~,~y=1)\)
最小値 \(-5~(x=-2~,~y=1)\)
次のページ「3章 三角関数」