2章 図形と方程式

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学Ⅱ 1章 方程式・式と証明
Advanced数学Ⅱ 2章 図形と方程式
Advanced数学Ⅱ 3章 三角関数
Advanced数学Ⅱ 4章 指数関数・対数関数
Advanced数学Ⅱ 5章 微分と積分
2章 図形と方程式
1節 点と直線
\({\small (2)}~\)正三角形
→ 平面上の三角形の形状

互いに垂直:②と③
\({\rm A}(a~,~b)\) \({\rm B}(-c~,~0)\)
\({\rm C}(2c~,~0)\) \({\rm D}(0~,~0)\)
このとき、
\({\rm AB}^2=(-c-a)^2+(-b)^2\)
\(=a^2+b^2+c^2+2ca\)
\({\rm AC}^2=(2c-a)^2+(-b)^2\)
\(=a^2+b^2+4c^2-4ca\)
よって、
\(2{\rm AB}^2+{\rm AC}^2\)
\(=3(a^2+b^2+2c^2)\)
また、
\({\rm AD}^2=a^2+b^2\)
\({\rm BD}^2=(-c)^2=c^2\)
よって、
\({\rm AD}^2+2{\rm BD}^2\)
\(=a^2+b^2+2c^2\)
したがって、
\(2{\rm AB}^2+{\rm AC}^2=3({\rm AD}^2+2{\rm BD}^2)\) [終]
→ 座標を利用した等式の証明
\({\rm A}(a~,~b)~,~{\rm B}(-c~,~0)~,~{\rm C}(c~,~0)\)
とすると、
直線 \({\rm AB}\) の傾きが \({\large \frac{b}{a+c}}\) で、辺 \({\rm AB}\) の中点が \(\left({\large \frac{a-c}{2}}~,~{\large \frac{b}{2}}\right)\) より、辺 \({\rm AB}\) の垂直二等分線の方程式は、$$~~~y-\frac{b}{2}=-\frac{a+c}{b}\left(x-\frac{a-c}{2}\right)$$$$~\Leftrightarrow~y=-\frac{a+c}{b}x+\frac{a^2+b^2-c^2}{2b}$$これを①とする
次に、直線 \({\rm AC}\) の傾きが \({\large \frac{b}{a-c}}\) で、辺 \({\rm AC}\) の中点が \(\left({\large \frac{a+c}{2}}~,~{\large \frac{b}{2}}\right)\) より、辺 \({\rm AC}\) の垂直二等分線の方程式は、$$~~~y-\frac{b}{2}=-\frac{a-c}{b}\left(x-\frac{a+c}{2}\right)$$$$~\Leftrightarrow~y=-\frac{a-c}{b}x+\frac{a^2+b^2-c^2}{2b}$$これを②とする
①と②を連立すると、交点は$$~~~\left(0~,~\frac{a^2+b^2-c^2}{2b}\right)$$これは、\(y\) 軸上のの点で辺 \({\rm BC}\) 上にある
したがって、三角形の3辺の垂直二等分線は、1点で交わる [終]
それぞれの直線の傾きは、
\(-{\large \frac{a_1}{b_1}}~,~-{\large \frac{a_2}{b_2}}\)
これより、2直線が平行となるので、
\(-{\large \frac{a1}{b_1}}=-{\large \frac{a_2}{b_2}}\)
式変形すると、
\(a_1b_2-a_2b_1=0\)
したがって、
2直線が平行\(~~\Leftrightarrow~~a_1b_2-a_2b_1=0\)
また、2直線が垂直となるので、
\(\left(-{\large \frac{a_1}{b_1}}\right)\left(-{\large \frac{a_2}{b_2}}\right)=-1\)
式変形すると、
\(a_1a_2+b_1b_2=0\)
したがって、
2直線が垂直\(~~\Leftrightarrow~~a_1a_2+b_1b_2=0\)
[終]
2節 円
\({\small (2)}~\)中心 \((0~,~-{\large \frac{\,5\,}{2}})\)、半径 \({\large \frac{\sqrt{\,17\,}}{2}}\) の円
\({\small (3)}~\)点 \((-2~,~5)\)
→ 円の方程式
→ 円の方程式の決定①(点の条件)
\({\small (2)}~\)共有点1個
\({\small (3)}~\)共有点なし
3節 軌跡と領域
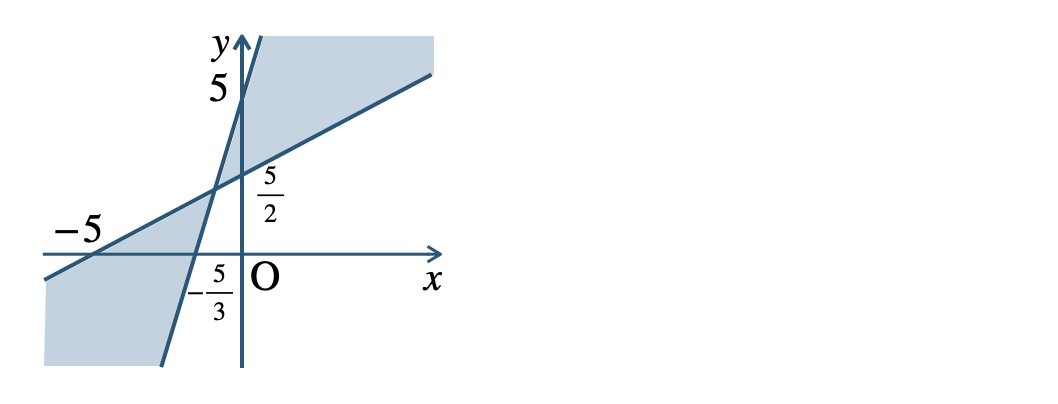
→ 軌跡①
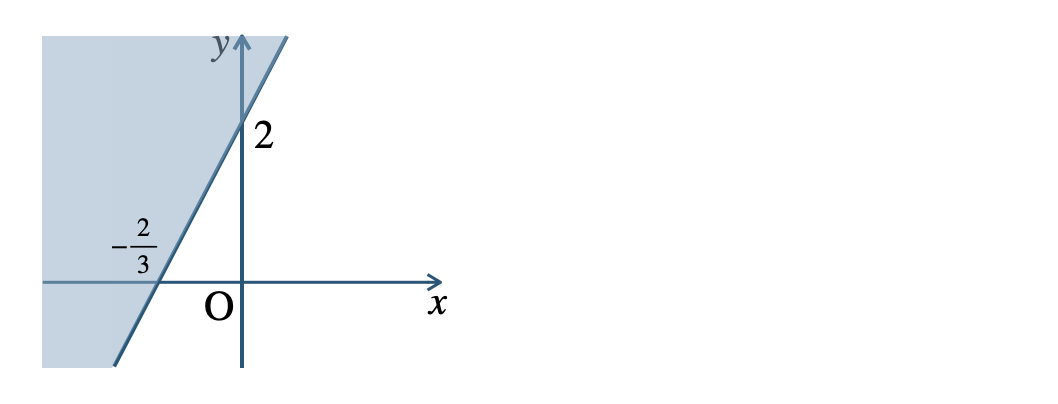
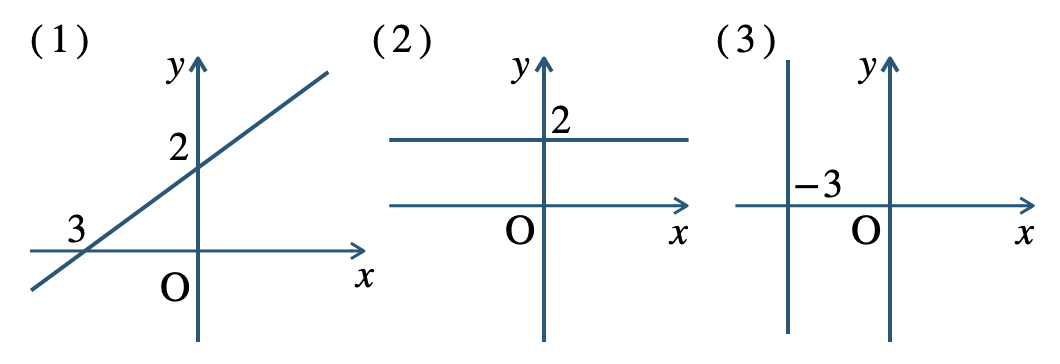
\({\small (2)}~\)境界線を含む
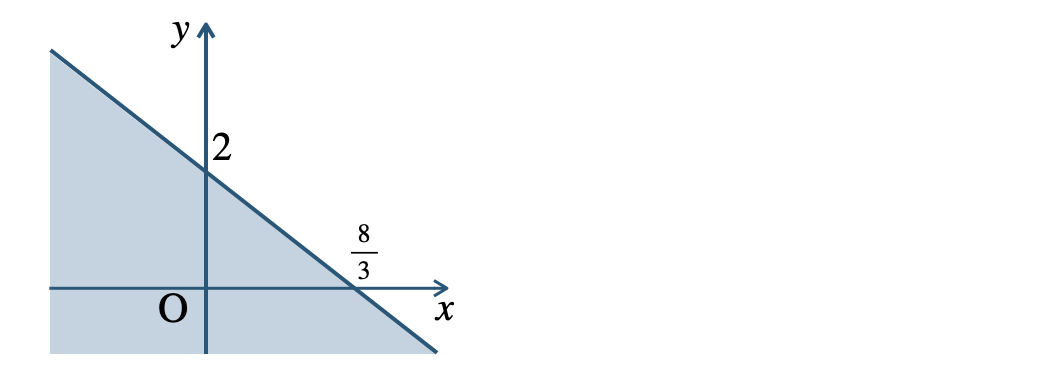
\({\small (3)}~\)境界線を含まない
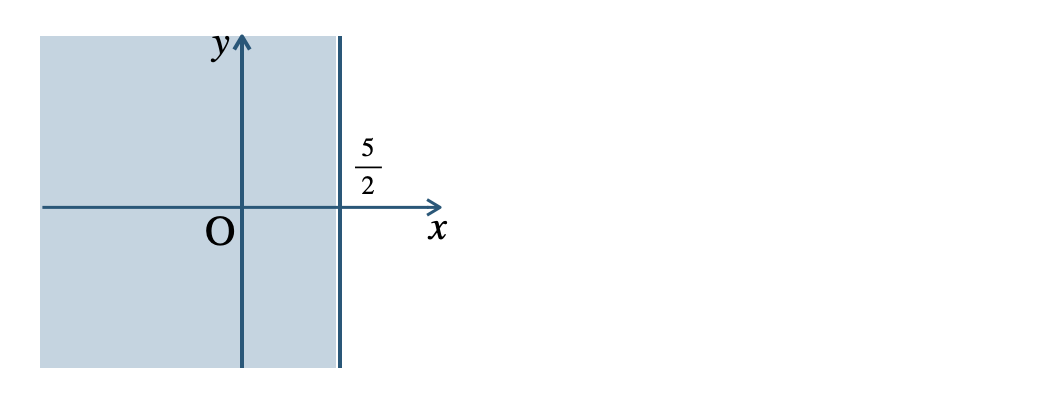
\({\small (4)}~\)境界線を含む

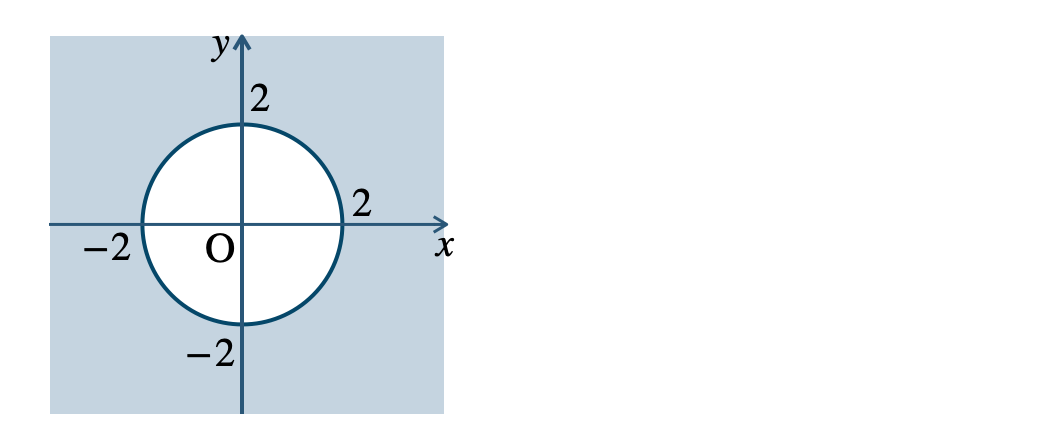
\({\small (2)}~\)境界線を含む
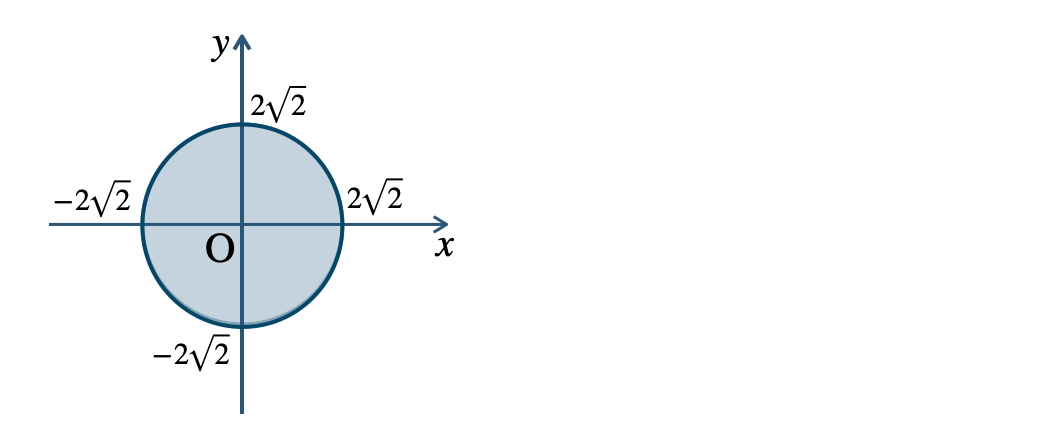
\({\small (3)}~\)境界線を含まない

\({\small (4)}~\)境界線を含む
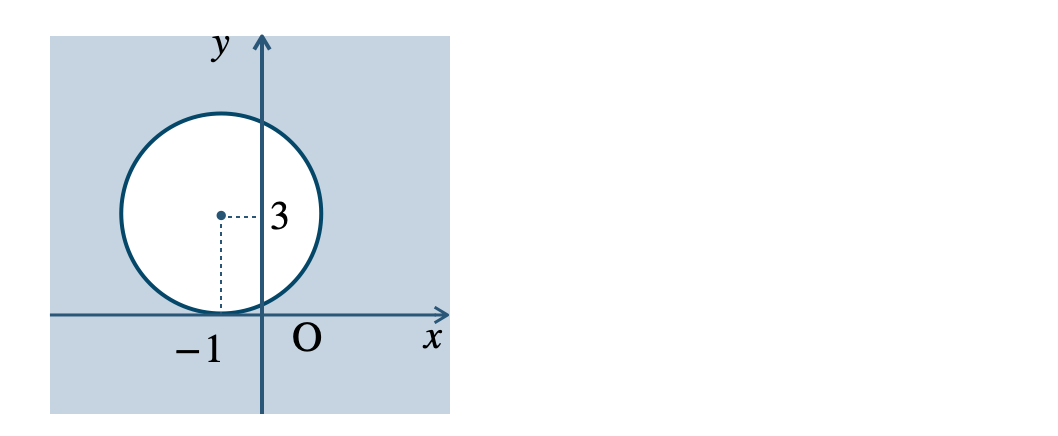
→ 不等式の表す領域

x > 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第2象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y > 0
\end{array}\right.\end{eqnarray}$$第3象限$$\begin{eqnarray} \left\{\begin{array}{l}
x < 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$第4象限$$\begin{eqnarray} \left\{\begin{array}{l}
x > 0 \\ y < 0
\end{array}\right.\end{eqnarray}$$
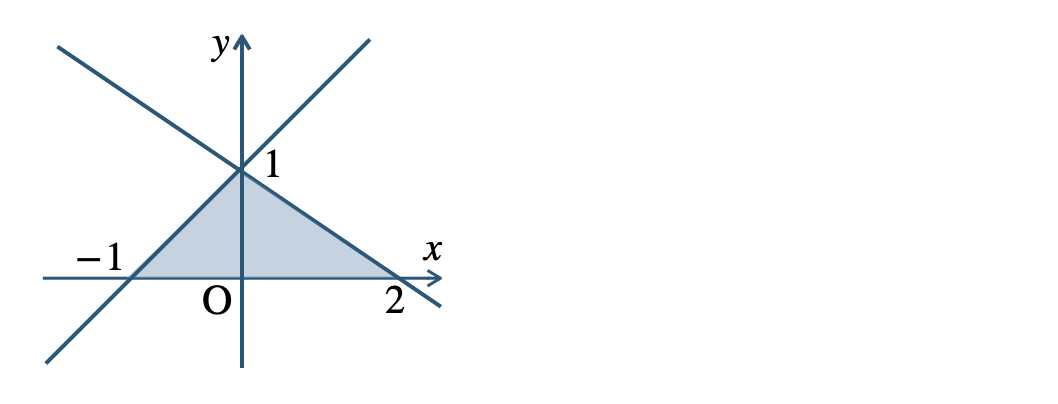
[証明] \(x^2+y^2≦8\) の領域を \(P\)、\(x+y≦4\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになり、境界線を含む
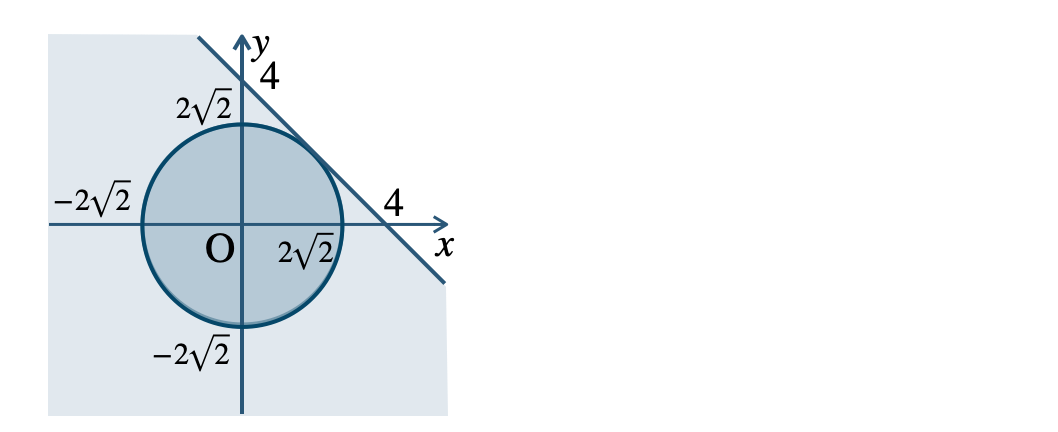
これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2≦8~\Rightarrow~x+y≦4\)
[終]
\({\small (2)}~\)
[証明] \(x^2+y^2-6x-8y<0\) の領域を \(P\)、\(x>0\) または \(y>0\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2-6x-8y<0\)
\(~\Rightarrow~x>0\) または \(y>0\)
[終]
→ 領域を用いた証明
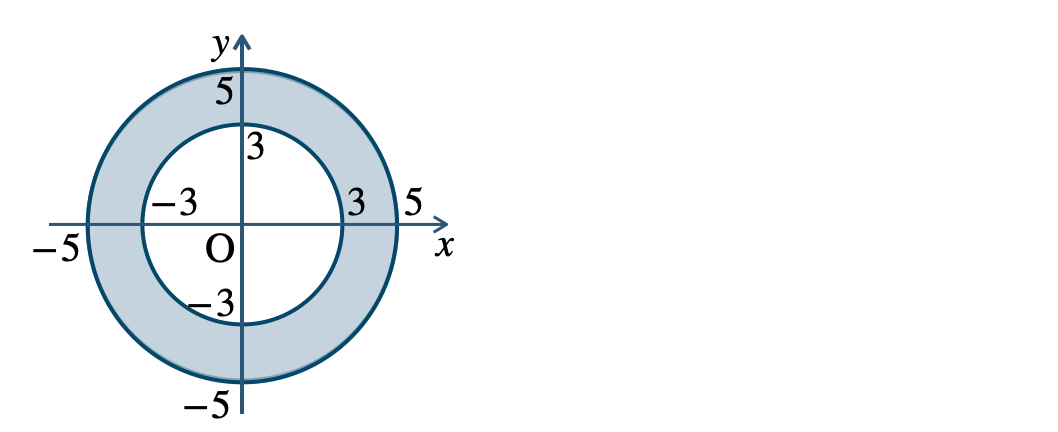
\({\small (2)}~\)境界線を含む
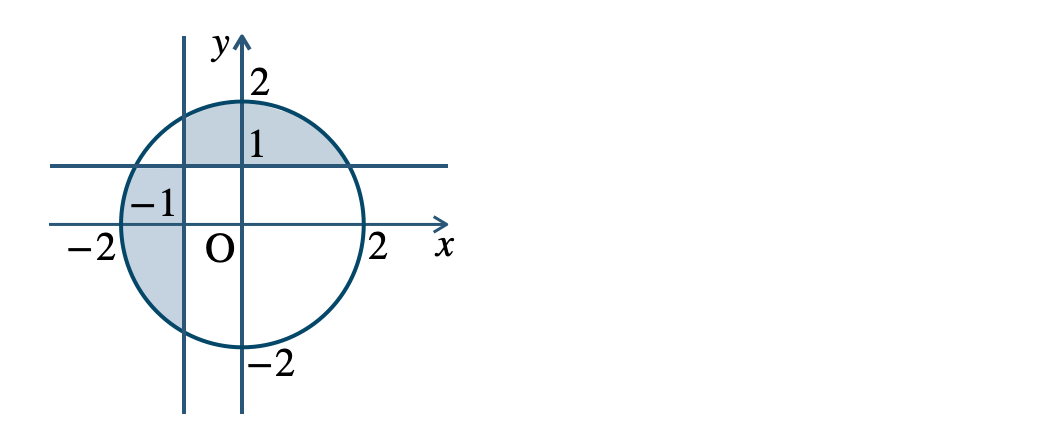
\({\small (3)}~\)境界線を含まない
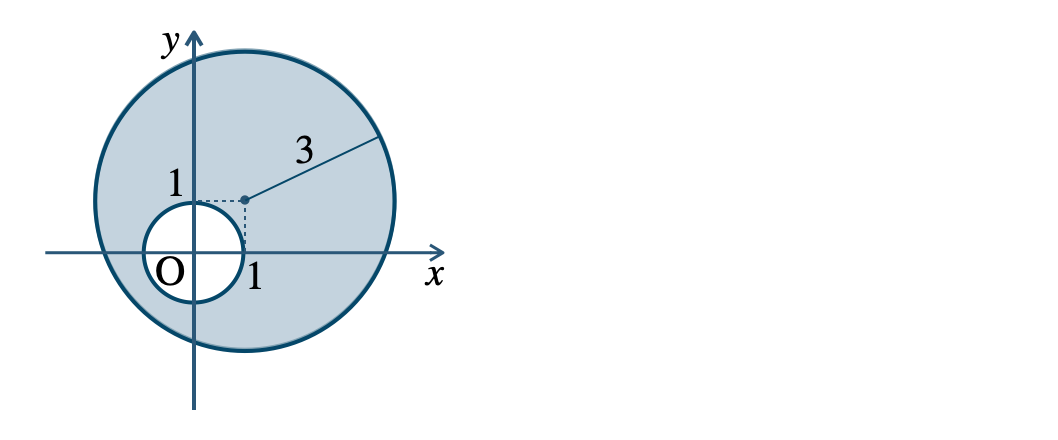
\({\small (4)}~\)境界線を含まない
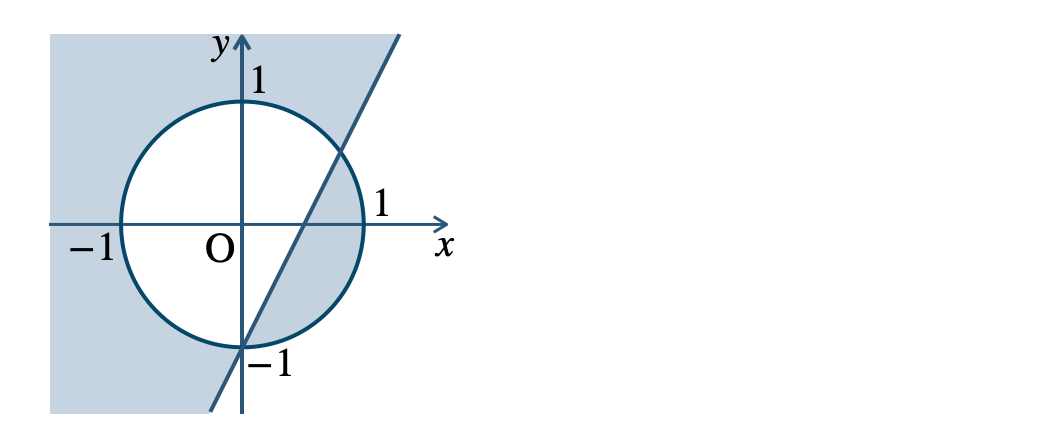
[証明] \(x^2+y^2-6x+8y+16<0\) の領域を \(P\)、\(x>0\) または \(y<0\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになる

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2-6x+8y+16<0\)
\(~\Rightarrow~x>0\) または \(y<0\)
[終]
\({\small (2)}~\)
[証明] \(x^2+y^2+2x-4y≧15\) の領域を \(P\)、\(x^2+y^2≧5\) の領域を \(Q\) とする
これらの領域を図示すると次の図のようになり、境界線を含む

これより、\(P\subset Q\) が成り立つ
したがって、
\(x^2+y^2+2x-4y≧15\)
\(~\Rightarrow~x^2+y^2≧5\)
[終]
\({\small (2)}~\)境界線を含む



練習問題 図形と方程式
\({\rm A}(0~,~0)\) \({\rm B}(a~,~0)\)
\({\rm C}(a~,~b)\) \({\rm D}(0~,~b)\)
また、任意の点を \({\rm P}(x~,~y)\)
このとき、
\({\rm PA}^2=x^2+y^2\)
\({\rm PC}^2=(x-a)^2+(y-b)^2\)
よって、
\({\rm PA}^2+{\rm PC}^2\)
\(=x^2+y^2+(x-a)^2+(y-b)^2\)
また、
\({\rm PB}^2=(x-a)^2+y^2\)
\({\rm PD}^2=x^2+(y-b)^2\)
よって、
\({\rm PB}^2+{\rm PD}^2\)
\(=x^2+y^2+(x-a)^2+(y-b)^2\)
したがって、
\({\rm PA}^2+{\rm PC}^2={\rm PB}^2+{\rm PD}^2\) [終]
$${\small (2)}~{ \frac{\,|x_1y_2-x_2y_1|\,}{\,\sqrt{x_1^2+y_1^2}\,}}$$\({\small (3)}~\)[証明]
\(\triangle {\rm OAB}\) の底辺を \({\rm OA}\)、高さを \({\rm AB}\) とする
(1)と(2)の解を用いると、
\(\triangle {\rm OAB}\)
\(={\large \frac{1}{\,2\,}}\cdot{\rm OA}\cdot d\)
\(={\large \frac{1}{\,2\,}}\cdot\sqrt{x_1^2+y_1^2}\cdot{\large \frac{\,|x_1y_2-x_2y_1|\,}{\sqrt{x_1^2+y_1^2}}}\)
\(={\large \frac{1}{\,2\,}}|x_1y_2-x_2y_1|\)
[終]
次のページ「3章 三角関数」