このページは、東京書籍:Advanced数学Ⅰ[701]
1章 数と式
1章 数と式

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学Ⅰ 1章 数と式
Advanced数学Ⅰ 2章 集合と論証
Advanced数学Ⅰ 3章 2次関数
Advanced数学Ⅰ 4章 図形と計量
Advanced数学Ⅰ 5章 データの分析
1章 数と式
1節 式の計算
p.6 問1\({\small (1)}~\)次数 \(4\)、係数 \(5\)
\({\small (2)}~\)次数 \(4\)、係数 \(1\)
\({\small (3)}~\)次数 \(0\)、係数 \(-7\)
\({\small (2)}~\)次数 \(4\)、係数 \(1\)
\({\small (3)}~\)次数 \(0\)、係数 \(-7\)
p.7 問3$$~~~-4x^2y+9xy-4$$
p.7 問4 \(x\) については3次式、\(-y^2-4y+1\)
\(y\) については3次式、\(x^3+7x+1\)
\(y\) については3次式、\(x^3+7x+1\)
p.7 問5$${\small (1)}~7x^3+5x^2-3x-2$$$${\small (2)}~2x^2+(5y-1)x+(y^2+5y-4)$$→ 多項式の次数と定数項
p.8 問6$${\small (1)}~{\rm A+B}=4x^3-9x^2-x$$$$~~~~~~{\rm A-B}=-2x^3+x^2+x-6$$$${\small (2)}~{\rm A+B}=x^2-3xy+2y^2$$$$~~~~~~{\rm A-B}=3x^2+3xy$$
p.8 問7$${\small (1)}~11x-14$$$${\small (2)}~7x^2+x+7$$$${\small (3)}~11x^2-11x+27$$→ 多項式の計算
p.9 問8$${\small (1)}~a^8$$$${\small (2)}~a^3b^9$$$${\small (3)}~x^{17}$$$${\small (4)}~x^{11}y^{14}$$
p.9 問9$${\small (1)}~{ \frac{\,1\,}{\,2\,}}a^7$$$${\small (2)}~-4a^8b^5$$$${\small (3)}~81x^{14}$$$${\small (4)}~2x^8y^{11}$$→ 累乗の計算
p.10 問10$${\small (1)}~6x^2-21x$$$${\small (2)}~15x^5-10x^4+5x^3$$$${\small (3)}~-8x^3y+4x^2y^2-4xy^3$$
p.10 問11$${\small (1)}~2x^2+15x+18$$$${\small (2)}~15x^2+23x-28$$$${\small (3)}~2x^3-27x+20$$$${\small (4)}~8x^3-32x^2+20x-21$$→ 分配法則と展開
p.11 問12$${\small (1)}~9x^2+6xy+y^2$$$${\small (2)}~64x^2-48xy+9y^2$$$${\small (3)}~36x^2-25y^2$$$${\small (4)}~x^2-5x-14$$
p.11 問13$${\small (1)}~10x^2+9x+2$$$${\small (2)}~6x^2+7x-20$$
p.12 問14$${\small (1)}~4x^2-13xy+3y^2$$$${\small (2)}~12x^2-5xy-2y^2$$→ 2次式の展開と乗法公式
p.12 問15$${\small (1)}~a^2+2ab+b^2-5a-5b$$$${\small (2)}~a^2-2ab+b^2-4a+4b-21$$$${\small (3)}~x^2-2xz+z^2-y^2$$$${\small (4)}~x^2-y^2+2yz-z^2$$
p.12 問16$${\small (1)}~a^2+b^2+c^2+2ab-2bc-2ca$$$${\small (2)}~a^2+b^2+c^2-2ab+2bc-2ca$$$${\small (3)}~x^2+4y^2+9z^2-4xy-12yz+6zx$$
p.13 問17①$$\begin{split}&(x+2)(x+3)(x-2)(x-3)\\[2pt]~~=~&\{(x+2)(x+3)\}\{(x-2)(x-3)\}\\[2pt]~~=~&(x^2+5x+6)(x^2-5x+6)\\[2pt]~~=~&\{(x^2+6)+5x\}\{(x^2+6)-5x\}\\[2pt]~~=~&(x^2+6)^2-(5x)^2\\[2pt]~~=~&x^4+12x^2+36-25x^2\\[2pt]~~=~&x^4-13x^2+36\end{split}$$
②$$\begin{split}&(x+2)(x+3)(x-2)(x-3)\\[2pt]~~=~&\{(x+2)(x-3)\}\{(x+3)(x-2)\}\\[2pt]~~=~&(x^2-x-6)(x^2+x-6)\\[2pt]~~=~&\{(x^2-6)-x\}\{(x^2-6)+x\}\\[2pt]~~=~&(x^2-6)^2-x^2\\[2pt]~~=~&x^4-12x^2+36-x^2\\[2pt]~~=~&x^4-13x^2+36\end{split}$$
②$$\begin{split}&(x+2)(x+3)(x-2)(x-3)\\[2pt]~~=~&\{(x+2)(x-3)\}\{(x+3)(x-2)\}\\[2pt]~~=~&(x^2-x-6)(x^2+x-6)\\[2pt]~~=~&\{(x^2-6)-x\}\{(x^2-6)+x\}\\[2pt]~~=~&(x^2-6)^2-x^2\\[2pt]~~=~&x^4-12x^2+36-x^2\\[2pt]~~=~&x^4-13x^2+36\end{split}$$
p.13 問18$${\small (1)}~x^4-29x^2+100$$$${\small (2)}~x^4+10x^3+35x^2+50x+24$$$${\small (3)}~a^4-8a^2b^2+16b^4$$$${\small (4)}~16x^4-72x^2y^2+81y^4$$
p.13 問19$$~~~a^4-1$$→ 式の展開の工夫
p.14 問20$${\small (1)}~3a(3ab-2c)$$$${\small (2)}~xy(3z^2+1)$$$${\small (3)}~3a^2b^2(a-2b+4c)$$
p.14 問21$${\small (1)}~(x+5y)(y-z)$$$${\small (2)}~(4x+1)(y-2)$$$${\small (3)}~(3a-b)(x-1)$$$${\small (4)}~(a+2)(b-c)$$
p.15 問22$${\small (1)}~(4x+1)^2$$$${\small (2)}~(2x-7y)^2$$$${\small (3)}~(8x+9y)(8x-9y)$$$${\small (4)}~(x-2)(x+15)$$
p.15 問23$${\small (1)}~x^2(5x+2y)(5x-2y)$$$${\small (2)}~a(x+6)^2$$$${\small (3)}~x(x+6)(x-8)$$$${\small (4)}~(a-b)(x+y)(x-y)$$→ 2次式の因数分解
p.16 問24$${\small (1)}~(x+1)(2x+1)$$$${\small (2)}~(x-2)(3x+1)$$$${\small (3)}~(x+2)(5x-3)$$$${\small (4)}~(2x-1)(4x+5)$$$${\small (5)}~(2x-3)(3x+2)$$$${\small (6)}~(2x-3)(2x-5)$$
p.17 問25$${\small (1)}~(x+y)(7x+4y)$$$${\small (2)}~(3x+2y)(4x-3y)$$→ 因数分解(たすき掛け)
→ 【問題演習】因数分解(たすき掛け)
→ 【問題演習】因数分解(たすき掛け)
p.17 問26$${\small (1)}~(a+5b)(a+3b)$$$${\small (2)}~(3x+y-z)(3x-y+z)$$$${\small (3)}~(x-y+9)(x-y-5)$$$${\small (4)}~(2a+b-4)(2a+b-5)$$→ 因数分解の工夫
p.18 問27$${\small (1)}~(2y+1)(2y-1)(x-1)$$$${\small (2)}~(a+3b)(a-3b)(a+c)$$→ 2種類以上の文字を含む式の因数分解①(1次式)
p.18 問28$$\begin{split}&4y^2+(9x+6)y+2x^2+5x+2\\[2pt]~~=~&4y^2+(9x+6)y+(2x+1)(x+2)\\[2pt]~~=~&\{4y+(x+2)\}\{y+(2x+1)\}\\[2pt]~~=~&(4y+x+2)(y+2x+1)\end{split}$$
p.18 問29$${\small (1)}~(2x+y+1)(x+2y-3)$$$${\small (2)}~(x-y+2)(2x+y+1)$$
p.20 参考 問1$${\small (1)}~(x+2)(x-2)(x+3)(x-3)$$$${\small (2)}~(2x+1)(2x-1)(2x^2+3)$$
p.20 参考 問2$${\small (1)}~(x^2+x+1)(x^2-x+1)$$$${\small (2)}~(3x^2+x-1)(3x^2-x-1)$$→ 複2次式の因数分解
p.21 発展 問1$$\begin{split}{\small (1)}~&(a+b)^3\\[2pt]~~=~&(a+b)(a+b)^2\\[2pt]~~=~&(a+b)(a^2+2ab+b^2)\\[2pt]~~=~&a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\[2pt]~~=~&a^3+3a^2b+3ab^2+b^3\end{split}$$$$\begin{split}{\small (2)}~&(a-b)^3\\[2pt]~~=~&(a-b)(a-b)^2\\[2pt]~~=~&(a-b)(a^2-2ab+b^2)\\[2pt]~~=~&a^3-2a^2b+ab^2-a^2b+2ab^2-b^3\\[2pt]~~=~&a^3-3a^2b+3ab^2-b^3\end{split}$$
p.21 発展 問2$${\small (1)}~x^3+3x^2+3x+1$$$${\small (2)}~8x^3-12x^2y+6xy^2-y^3$$→ 3次式の展開
p.21 発展 問3$$\begin{split}{\small (1)}~&(a+b)(a^2-ab+b^2)\\[2pt]~~=~&a^3-a^2b+ab^2+a^2b-ab^2+b^3\\[2pt]~~=~&a^3+b^3\end{split}$$$$\begin{split}{\small (2)}~&(a-b)(a^2+ab+b^2)\\[2pt]~~=~&a^3+a^2b+ab^2-a^2b-ab^2-b^3\\[2pt]~~=~&a^3-b^3\end{split}$$
p.21 発展 問4$${\small (1)}~(x+5)(x^2-5x+25)$$$${\small (2)}~(4x-3y)(16x^2+12xy+9y^2)$$→ 3次式の因数分解
2節 実数
p.22 問1$${\small (1)}~{ \frac{\,51\,}{\,25\,}}$$$${\small (2)}~{ \frac{\,5\,}{\,8\,}}$$
p.23 問2$${\small (1)}~0.3\dot{8}$$$${\small (2)}~0.\dot{1}\dot{8}$$$${\small (3)}~0.1\dot{2}\dot{7}$$$${\small (4)}~1.\dot{2}9\dot{7}$$
p.23 問3$${\small (1)}~{ \frac{\,4\,}{\,33\,}}$$$${\small (2)}~{ \frac{\,11\,}{\,90\,}}$$$${\small (3)}~{ \frac{\,137\,}{\,111\,}}$$→ 循環小数と分数
p.23 問4 有理数 \({\large \frac{\,1\,}{\,7\,}}~,~0.2\dot{3}~,~\sqrt{25}\)
無理数 \(2\pi~,~\sqrt{7}\)
無理数 \(2\pi~,~\sqrt{7}\)
p.25 問5
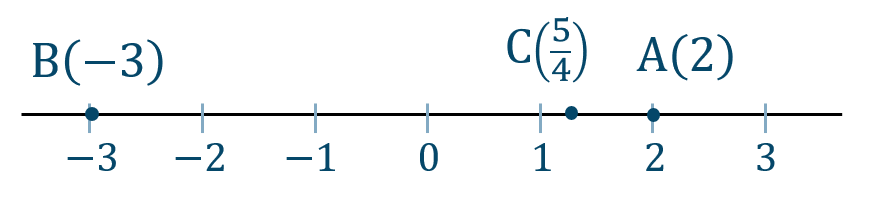
p.25 問6$${\small (1)}~2.5$$$${\small (2)}~{ \frac{\,1\,}{\,3\,}}$$$${\small (3)}~0$$
p.26 問7$${\small (1)}~1$$$${\small (2)}~{ \frac{\,1\,}{\,12\,}}$$$${\small (3)}~\sqrt{3}-1$$
→ 絶対値の計算
→ 絶対値の計算
p.26 問8$${\small (1)}~3$$$${\small (2)}~7$$$${\small (3)}~6$$
p.26 問9\(a=-2\) のとき、$$~~~|-a|=|-(-2)|=|2|=2$$$$~~~|a|=|-2|=2$$したがって、\(|-a|=|a|\)
\(a=-2\) のとき、$$~~~|a|^2=|-2|^2=4$$$$~~~a^2=(-2)^2=4$$したがって、\(|a|^2=a^2\)
\(a=-2\) のとき、$$~~~|a|^2=|-2|^2=4$$$$~~~a^2=(-2)^2=4$$したがって、\(|a|^2=a^2\)
p.26 問10\(a=-3~,~b=2\) のとき、$$~~~|ab|=|(-3)\cdot2|=|-6|=6$$$$~~~|a||b|=|-3|\cdot|2|=3\cdot2=6$$したがって、\(|ab|=|a||b|\)
\(a=-3~,~b=2\) のとき、$$~~~\left|{ \frac{\,a\,}{\,b\,}}\right|=\left|{ \frac{\,-3\,}{\,2\,}}\right|={ \frac{\,3\,}{\,2\,}}$$$$~~~{ \frac{\,|a|\,}{\,|b|\,}}={ \frac{\,|-3|\,}{\,|2|\,}}={ \frac{\,3\,}{\,2\,}}$$したがって、$$~~~\left|{ \frac{\,a\,}{\,b\,}}\right|={ \frac{\,|a|\,}{\,|b|\,}}$$
\(a=-3~,~b=2\) のとき、$$~~~\left|{ \frac{\,a\,}{\,b\,}}\right|=\left|{ \frac{\,-3\,}{\,2\,}}\right|={ \frac{\,3\,}{\,2\,}}$$$$~~~{ \frac{\,|a|\,}{\,|b|\,}}={ \frac{\,|-3|\,}{\,|2|\,}}={ \frac{\,3\,}{\,2\,}}$$したがって、$$~~~\left|{ \frac{\,a\,}{\,b\,}}\right|={ \frac{\,|a|\,}{\,|b|\,}}$$
p.27 問11$${\small (1)}~\pm\sqrt{17}$$$${\small (2)}~\pm5$$$${\small (3)}~12$$
p.27 問12$$~~~-a+1$$
p.28 問13\({\large \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}\) を2乗すると、$$~~~\left({ \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}\right)^2={ \frac{\,a\,}{\,b\,}}$$
次に、\(\sqrt{{\large \frac{\,a\,}{\,b\,}}}\) を2乗すると、$$~~~\left(\sqrt{{ \frac{\,a\,}{\,b\,}}}\right)^2={ \frac{\,a\,}{\,b\,}}$$ここで、\({\large \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}>0~,~\sqrt{{\large \frac{\,a\,}{\,b\,}}}>0\) より、$$~~~{ \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}=\sqrt{{ \frac{\,a\,}{\,b\,}}}$$
次に、\(\sqrt{{\large \frac{\,a\,}{\,b\,}}}\) を2乗すると、$$~~~\left(\sqrt{{ \frac{\,a\,}{\,b\,}}}\right)^2={ \frac{\,a\,}{\,b\,}}$$ここで、\({\large \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}>0~,~\sqrt{{\large \frac{\,a\,}{\,b\,}}}>0\) より、$$~~~{ \frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}}=\sqrt{{ \frac{\,a\,}{\,b\,}}}$$
p.28 問14$${\small (1)}~2\sqrt{6}$$$${\small (2)}~10\sqrt{17}$$$${\small (3)}~-\sqrt{2}$$$${\small (4)}~{ \frac{\,5\sqrt{5}\,}{\,3\,}}+2\sqrt{2}$$
p.29 問15$${\small (1)}~4$$$${\small (2)}~16-4\sqrt{15}$$→ 平方根の計算
p.29 問16$${\small (1)}~{ \frac{\,\sqrt{7}\,}{\,14\,}}$$$${\small (2)}~{ \frac{\,\sqrt{22}\,}{\,11\,}}$$$${\small (3)}~{ \frac{\,\sqrt{15}\,}{\,5\,}}$$
p.29 問17$${\small (1)}~{ \frac{\,\sqrt{6}-\sqrt{3}\,}{\,3\,}}$$$${\small (2)}~3+\sqrt{6}$$$${\small (3)}~{ \frac{\,7+3\sqrt{5}\,}{\,2\,}}$$→ 分母の有理化
p.30 問18$${\small (1)}~\sqrt{7}$$$${\small (2)}~{ \frac{\,1\,}{\,2\,}}$$$${\small (3)}~6$$→ 対称式
p.30 発展 問1$$~~~{ \frac{\,11\sqrt{7}\,}{\,2\,}}$$
p.31 問19 整数部分 \(3\)、小数部分 \(\sqrt{10}-3\)
p.34 発展 問1$${\small (1)}~\sqrt{3}+1$$$${\small (2)}~2-\sqrt{2}$$$${\small (3)}~\sqrt{6}+1$$$${\small (4)}~2-\sqrt{3}$$$${\small (5)}~\sqrt{7}+2$$$${\small (6)}~{ \frac{\,\sqrt{10}-\sqrt{2}\,}{\,2\,}}$$→ 二重根号
p.35 発展 問1 ①と③
p.35 発展 問2 ① \(a^2+b^2=(a+b)^2-2ab=s^2-2t\)
③ \((a-b)^2=(a+b)^2-4ab=s^2-4t\)
③ \((a-b)^2=(a+b)^2-4ab=s^2-4t\)
p.35 発展 問3 ②と③
3節 1次不等式
p.36 問1$$~~~3a+4b≦500$$
p.37 問2\({\small (1)}~a=-4~,~b=2\) のとき、
\(a+3=-1~,~b+3=5\) より、$$~~~a+3< b+3$$となる
次に、\(a-2=-6~,~b-2=0\) より、$$~~~a-2< b-2$$となる
次に、\(2a=-8~,~2b=4\) より、$$~~~2a< 2b$$となる
また、\({\large \frac{\,a\,}{\,2\,}}=-2~,~{\large \frac{\,b\,}{\,2\,}}=1\) より、$$~~~{ \frac{\,a\,}{\,2\,}}<{ \frac{\,b\,}{\,2\,}}$$となる
\({\small (2)}~a=10~,~b=-6\) のとき、
\(a+3=-7~,~b+3=-3\) より、$$~~~a+3< b+3$$ となる
次に、\(a-2=-12~,~b-2=-8\) より、$$~~~a-2< b-2$$ となる
次に、\(2a=-20~,~2b=-12\) より、$$~~~2a< 2b$$ となる
また、\({\large \frac{\,a\,}{\,2\,}}=-5~,~{\large \frac{\,b\,}{\,2\,}}=-3\) より、$$~~~{ \frac{\,a\,}{\,2\,}}<{ \frac{\,b\,}{\,2\,}}$$ となる
\(a+3=-1~,~b+3=5\) より、$$~~~a+3< b+3$$となる
次に、\(a-2=-6~,~b-2=0\) より、$$~~~a-2< b-2$$となる
次に、\(2a=-8~,~2b=4\) より、$$~~~2a< 2b$$となる
また、\({\large \frac{\,a\,}{\,2\,}}=-2~,~{\large \frac{\,b\,}{\,2\,}}=1\) より、$$~~~{ \frac{\,a\,}{\,2\,}}<{ \frac{\,b\,}{\,2\,}}$$となる
\({\small (2)}~a=10~,~b=-6\) のとき、
\(a+3=-7~,~b+3=-3\) より、$$~~~a+3< b+3$$ となる
次に、\(a-2=-12~,~b-2=-8\) より、$$~~~a-2< b-2$$ となる
次に、\(2a=-20~,~2b=-12\) より、$$~~~2a< 2b$$ となる
また、\({\large \frac{\,a\,}{\,2\,}}=-5~,~{\large \frac{\,b\,}{\,2\,}}=-3\) より、$$~~~{ \frac{\,a\,}{\,2\,}}<{ \frac{\,b\,}{\,2\,}}$$ となる
p.37 問3\({\small (1)}~a=−6~,~b=4\) のとき、
\(-2a=12~,~-2b=-8\) より、$$~~~-2a> -2b$$ となる
また、\({\large \frac{\,a\,}{\,-2\,}}=3~,~{\large \frac{\,b\,}{\,-2\,}}=-2\) より、$$~~~{ \frac{\,a\,}{\,-2\,}}>{ \frac{\,b\,}{\,-2\,}}$$ となる
\({\small (2)}~a=-8~,~b=-4\) のとき、
\(-2a=16~,~-2b=8\) より、$$~~~-2a> -2b$$ となる
また、\({\large \frac{\,a\,}{\,-2\,}}=4~,~{\large \frac{\,b\,}{\,-2\,}}=2\) より、$$~~~{ \frac{\,a\,}{\,-2\,}}>{ \frac{\,b\,}{\,-2\,}}$$ となる
\(-2a=12~,~-2b=-8\) より、$$~~~-2a> -2b$$ となる
また、\({\large \frac{\,a\,}{\,-2\,}}=3~,~{\large \frac{\,b\,}{\,-2\,}}=-2\) より、$$~~~{ \frac{\,a\,}{\,-2\,}}>{ \frac{\,b\,}{\,-2\,}}$$ となる
\({\small (2)}~a=-8~,~b=-4\) のとき、
\(-2a=16~,~-2b=8\) より、$$~~~-2a> -2b$$ となる
また、\({\large \frac{\,a\,}{\,-2\,}}=4~,~{\large \frac{\,b\,}{\,-2\,}}=2\) より、$$~~~{ \frac{\,a\,}{\,-2\,}}>{ \frac{\,b\,}{\,-2\,}}$$ となる
p.38 問4$$~~~x=3~,~4$$
p.39 問5$${\small (1)}~x>-6$$$${\small (2)}~x≦4$$$${\small (3)}~x < -{ \frac{\,9\,}{\,2\,}}$$
p.39 問6$${\small (1)}~x<2$$$${\small (2)}~x≧{ \frac{\,5\,}{\,2\,}}$$
p.39 問7$${\small (1)}~x<2$$$${\small (2)}~x≧-3$$$${\small (3)}~x<3$$$${\small (4)}~x≧{ \frac{\,14\,}{\,3\,}}$$→ 1次不等式の解
p.40 問8$${\small (1)}~-3< x < 1$$$${\small (2)}~2≦ x < 4$$$${\small (3)}~-{ \frac{\,1\,}{\,3\,}}≦ x ≦3$$
p.41 問9$${\small (1)}~x< -1$$$${\small (2)}~x≦ 4$$
p.41 問10$$~~~-15≦x≦-3$$→ 連立不等式の解
p.43 問12$${\small (1)}~x=6~,~-2$$$${\small (2)}~x=-3~,~-11$$$${\small (3)}~x=2~,~3$$
p.43 問13$${\small (1)}~-2< x < 2$$$${\small (2)}~-7≦x≦3$$$${\small (3)}~x< 1~,~4< x$$→ 絶対値を含む方程式と不等式
p.44 参考 問1$${\small (1)}~x=1~,~5$$$${\small (2)}~x=2$$
p.45 参考 問2$${\small (1)}~1≦x≦5$$$${\small (2)}~x< 1~,~4< x$$$${\small (3)}~x< -1$$→ 場合分けの必要な絶対値を含む方程式と不等式
p.46 問題 15 \(a< b\) となる \(a~,~b\) をとると、

よって、グラフより \(ac> bc\)
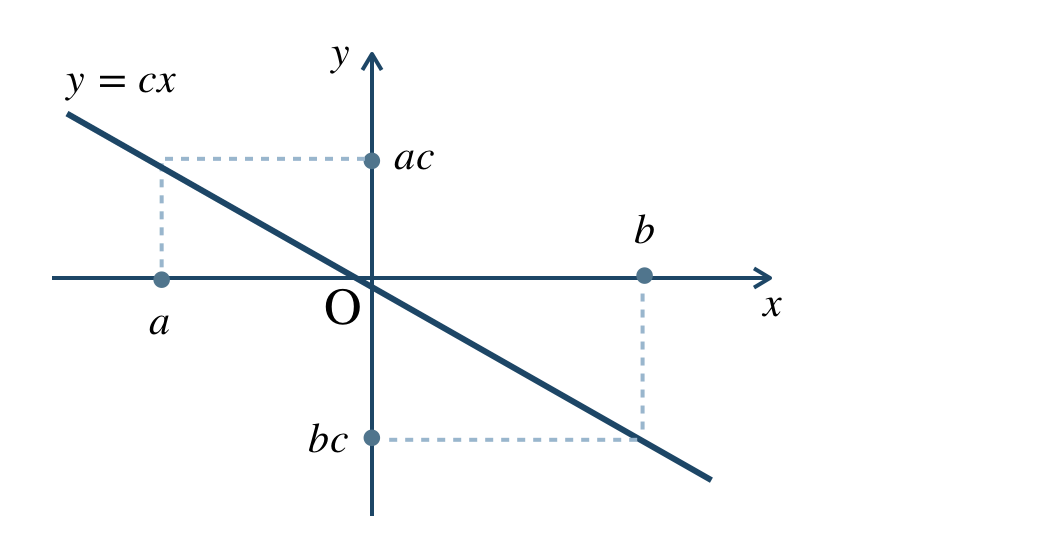
よって、グラフより \(ac> bc\)
次のページ「2章 集合と論証」


