【新課程】数研出版：数学Ⅰ[712]

p.8 練習1\({\small (1)}~\)係数 \(4\) 次数 \(5\)
\({\small (2)}~\)係数 \(-2\) 次数 \(2\)
\({\small (3)}~\)係数 \(-1\) 次数 \(6\)

p8 練習2\({\small (1)}~\)
　\(x\) について、係数 \(-5ay^2\) 次数 \(3\)
　\(y\) について、係数 \(-5ax^3\) 次数 \(2\)
　\(a\) について、係数 \(-5x^3y^2\) 次数 \(1\)
\({\small (2)}~\)
　\(x\) と \(y\) について、係数 \(2ab\) 次数 \(4\)
→ 単項式の次数と係数

p.9 練習3\({\small (1)}~x^2+6x-8\) ２次式
\({\small (2)}~-2a^2+8ab+2b^2\) ２次式
\({\small (3)}~-2x^3-8x^2+8x+4\) ３次式

p.9 深める②と④

p.10 練習4\({\small (1)}~\)
　\(x\) について、２次式で定数項 \(-3\)
　\(a\) について、１次式で定数項 \(x-3\)
\({\small (2)}~\)
　\(x\) について、２次式で定数項 \(ab\)
\({\small (3)}~\)
　\(x\) について、３次式で定数項 \(-y^2+1\)
　\(y\) について、２次式で定数項 \(5x^3+1\)
　\(x\) と \(y\) について、３次式で定数項 \(1\)
→ 多項式の次数と定数項

p.10 練習5$${\small (1)}~x^4-3x^3+2x^2+5x-1$$$${\small (2)}~2x^2+(y-7)x+(3y^2-2y+5)$$

p.11 練習6$${\small (1)}~{\rm A+B}=x^3-2x^2-7x-5$$$$~~~~~~{\rm A-B}=7x^3-4x^2-3x+9$$$${\small (2)}~{\rm A+B}=-2x^3-2x^2+2x$$$$~~~~~~{\rm A-B}=6x^3-2x-2$$$${\small (3)}~{\rm A+B}=2x^2+6xy-3y^2$$$$~~~~~~ {\rm A-B}=8x^2-2xy+y^2$$

p.12 練習7$$~~~4x^2-2xy-y^2$$→ 多項式の計算

p.13 練習8$${\small (1)}~14x^6$$$${\small (2)}~-12a^9b^4c^4$$$${\small (3)}~-72x^8y^9$$→ 累乗の計算

p.14 練習9$${\small (1)}~9x^4-15x^3+6x^2$$$${\small (2)}~-x^3y^2+2x^2y^3+3xy^4$$$${\small (3)}~x^4+x^3-6x^2-4x+8$$$${\small (4)}~x^5+4x^4+2x^3+5x^2-6$$$${\small (5)}~x^3+xy^2+2y^3$$$${\small (6)}~2x^2-xy-3y^2-3x+7y-2$$→ 分配法則と展開

p.14 練習10$${\small (1)}~4x^2+12x+9$$$${\small (2)}~4x^2-20xy+25y^2$$$${\small (3)}~16x^2-9$$$${\small (4)}~x^2+10x+16$$$${\small (5)}~x^2-7x+12$$$${\small (6)}~x^2+2xy-15y^2$$

p.15 問1[証明]$$\begin{split}&(ax+b)(cx+d)\\[2pt]~~=~&ax(cx+d)+b(cx+d)\\[2pt]~~=~&ax\cdot cx+ax\cdot d+b\cdot cx+b\cdot d\\[2pt]~~=~&acx^2+adx+bcx+bd\\[2pt]~~=~&acx^2+(ad+bc)x+bd\end{split}$$[終]

p.15 練習11$${\small (1)}~12x^2+28x+15$$$${\small (2)}~15x^2-34x-16$$$${\small (3)}~2x^2+5xy-3y^2$$$${\small (4)}~12x^2-19ax+5a^2$$→ ２次式の展開と乗法公式

p.15 深める　24の項ができる

p.16 練習12$${\small (1)}~a^2+b^2+c^2+2ab-2bc-2ca$$$${\small (2)}~x^2+4y^2+z^2-4xy-4yz+2zx$$

p.16 練習13$${\small (1)}~a^4-2a^2b^2+b^4$$$${\small (2)}~x^4-1$$$${\small (3)}~x^4+2x^2+9$$$${\small (4)}~x^2-y^2-z^2+2yz$$または、$$~~~~~~x^2-y^2+2yz-z^2$$→ 式の展開の工夫

p.17 練習14$${\small (1)}~2xy(x-3y+5z)$$$${\small (2)}~xyz(4y-xz+2)$$$${\small (3)}~(x-y)(a-b)$$$${\small (4)}~(5x-3)(y-2)$$

p.18 練習15$${\small (1)}~(x-4)^2$$$${\small (2)}~(2x+7y)^2$$$${\small (3)}~(3a-8b)^2$$$${\small (4)}~(4x+5y)(4x-5y)$$$${\small (5)}~(x+2)(x+4)$$$${\small (6)}~(x-3y)(x-2y)$$$${\small (7)}~(x+4y)(x-3y)$$$${\small (8)}~(x+3a)(x-5a)$$→ ２次式の因数分解

p.19 練習16$${\small (1)}~(2x+1)(x+1)$$$${\small (2)}~(4x-3)(x-3)$$$${\small (3)}~(3x+2)(2x-3)$$$${\small (4)}~(3x+y)(x-y)$$$${\small (5)}~(a-4b)(3a-2b)$$$${\small (6)}~(4x-a)(x+2a)$$→ 因数分解（たすき掛け）
→ 【問題演習】因数分解（たすき掛け）

p.19 練習17$${\small (1)}~(x+y-3)(x-y+3)$$$${\small (2)}~(x+3y-2)(x-3y-2)$$→ 因数分解の工夫

p.20 練習18$${\small (1)}~(x+1)(x-1)(x+2)(x-2)$$$${\small (2)}~(x+3)(x-3)(x^2+9)$$$${\small (3)}~(x+1)(x+2)(x-1)(x+4)$$→ 複２次式の因数分解

p.20 練習19$${\small (1)}~(x-y)(x+y+z)$$$${\small (2)}~(a-3)(a-3b+3)$$$${\small (3)}~(2x-1)(x+3y+1)$$→ ２種類以上の文字を含む式の因数分解①（１次式）

p.21 練習20$${\small (1)}~(x+y+3)(x+2y-1)$$$${\small (2)}~(x-y+1)(3x+2y+3)$$→ 文字式のたすき掛け
→ ２種類以上の文字を含む式の因数分解②（２次式）

p.21 練習21$$~~~(a-b)(b-c)(a-c)$$または、$$~~~-(a-b)(b-c)(c-a)$$

p.21 深める$$~~~(3y+2x-1)(2y+x+3)$$

p.22 発展 練習1$${\small (1)}~x^3+3x^2+3x+1$$$${\small (2)}~x^3-6x^2+12x-8$$$${\small (3)}~27a^3+27a^2b+9ab^2+b^3$$$${\small (4)}~8x^3-36x^2y+54xy^2-27y^3$$

p.23 発展 練習2$$\begin{split}&(a+b)(a^2-ab+b^2)\\[2pt]~~=~&a^3-a^2b+ab^2+a^2b-ab^2+b^3\\[2pt]~~=~&a^3+b^3\end{split}$$
$$\begin{split}&(a-b)(a^2+ab+b^2)\\[2pt]~~=~&a^3+a^2b+ab^2-a^2b-ab^2-b^3\\[2pt]~~=~&a^3-b^3\end{split}$$

p.23 発展 練習3$${\small (1)}~x^3+8$$$${\small (2)}~x^3-27$$$${\small (3)}~27x^3+y^3$$$${\small (4)}~8a^3-27b^3$$→ ３次式の展開

p.23 発展 練習4$${\small (1)}~(x+3)(x^2-3x+9)$$$${\small (2)}~(a-4)(a^2+4a+16)$$$${\small (3)}~(2x-5y)(4x^2+10xy+25y^2)$$→ ３次式の因数分解

p.25 練習22$${\small (1)}~0.125$$$${\small (2)}~0.\dot{8}$$$${\small (3)}~0.\dot{2}\dot{1}$$$${\small (4)}~1.0\dot{1}8\dot{5}$$

p.27 練習23$${\small (1)}~\frac{\,1\,}{\,9\,}$$$${\small (2)}~\frac{\,4\,}{\,33\,}$$$${\small (3)}~\frac{\,24\,}{\,37\,}$$$${\small (4)}~\frac{\,69\,}{\,11\,}$$→ 循環小数と分数

p.28 練習24　自然数○×○×
　整数○○○×
　有理数○○○○
　実数○○○○

p.29 練習25　整数部分 \(3\)、小数部分 \(\pi-3\)

p.30 練習26$${\small (1)}~\frac{\,3\,}{\,4\,}$$$${\small (2)}~2$$$${\small (3)}~8$$$${\small (4)}~\pi-3$$→ 絶対値の計算

p.30 練習27$${\small (1)}~2$$$${\small (2)}~7$$$${\small (3)}~4$$

p.31 練習28$${\small (1)}~\pm 7$$$${\small (2)}~5$$$${\small (3)}~7~,~15$$

p.31 深める　\(a\) が負のとき、成り立たない

p.32 問2公式４
[証明]
\({\large \frac{\sqrt{a}}{\sqrt{b}}}\) を２乗すると、$$~~~\left(\frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}\right)^2=\frac{\,\left(\sqrt{a}\right)^2\,}{\,\left(\sqrt{b}\right)^2\,}=\frac{\,a\,}{\,b\,}$$また、\(\sqrt{a}>0~,~\sqrt{b}>0\) より、$$~~~\frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}>0$$よって、\({\large \frac{\sqrt{a}}{\sqrt{b}}}\) は \({\large \frac{\,a\,}{\,b\,}}\) の正の平方根であるから、$$~~~\frac{\,\sqrt{a}\,}{\,\sqrt{b}\,}=\sqrt{\frac{\,a\,}{\,b\,}}$$[終]
 
公式５
[証明]
\(a>0~,~k>0\) より、$$~~~\sqrt{k^2a}=\sqrt{k^2}\sqrt{a}$$ここで、\(\sqrt{k^2}=k\) であるので、$$~~~\sqrt{k^2a}=k\sqrt{a}$$[終]

p.33 練習29$${\small (1)}~2\sqrt{3}$$$${\small (2)}~7\sqrt{2}$$$${\small (3)}~3$$$${\small (4)}~22-7\sqrt{6}$$$${\small (5)}~27+12\sqrt{2}$$$${\small (6)}~46-12\sqrt{14}$$→ 平方根の計算

p.33 練習30$${\small (1)}~3\sqrt{6}$$$${\small (2)}~2\sqrt{3}-3$$$${\small (3)}~\frac{7+2\sqrt{10}}{3}$$$${\small (4)}~6-\sqrt{21}$$→ 分母の有理化

p.34 練習31$${\small (1)}~\sqrt{7}$$$${\small (2)}~\frac{\,1\,}{\,2\,}$$$${\small (3)}~6$$$${\small (4)}~\frac{\sqrt{7}}{2}$$→ 対称式

p.35 発展 練習1$${\small (1)}~6$$$${\small (2)}~10\sqrt{2}$$$${\small (3)}~5$$

p.36 発展 練習1$${\small (1)}~\sqrt{5}+\sqrt{2}$$$${\small (2)}~3-\sqrt{3}$$$${\small (3)}~\frac{\sqrt{10}+\sqrt{2}}{2}$$→ 二重根号

p.38 練習32$${\small (1)}~x+8>3x$$$${\small (2)}~-4≦ \frac{x}{2}-5≦0$$$${\small (3)}~-3≦a+b<0$$

p.39 問3\({\small (1)}~\)\(a>0~,~b>0\) のとき、
\(3a~,~3b\) を数直線上で表すと、

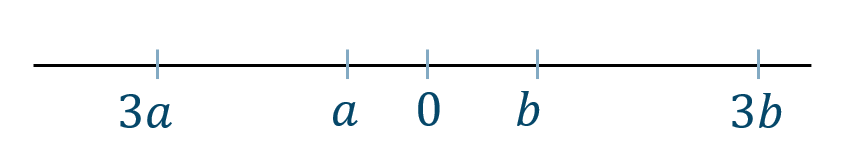
これより、大小関係が変わらないので、$$~~~3a<3b$$
また、\(-3a~,~-3b\) を数直線上で表すと、

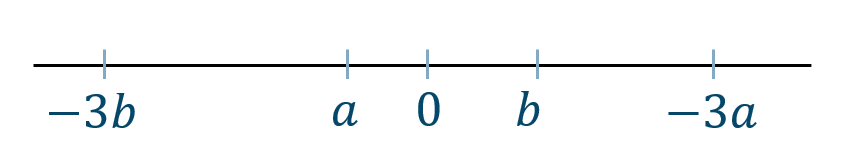
これより、大小関係が変わるので、$$~~~-3a>-3b$$
 
\({\small (2)}~\)\(a>0~,~b>0\) のとき、
\(3a~,~3b\) を数直線上で表すと、

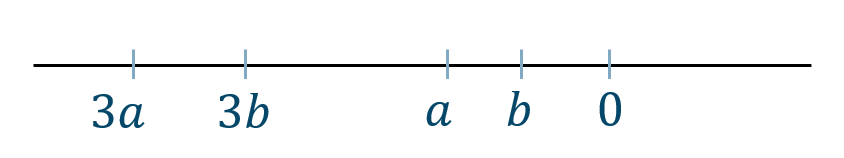
これより、大小関係が変わらないので$$~~~3a<3b$$
また、\(-3a~,~-3b\) を数直線上で表すと、

これより、大小関係が変わるので、$$~~~-3a>-3b$$

p.39 問4$${\small (1)}~<$$$${\small (2)}~>$$

p.40 練習33$${\small (1)}~<$$$${\small (2)}~>$$$${\small (3)}~>$$$${\small (4)}~>$$

p.41 練習34$${\small (1)}~x≦6$$$${\small (2)}~x≧-3$$$${\small (3)}~x<-4$$

p.41 深める例30
　両辺から \(5\) を引くと　←性質１
　両辺を正の数 \(3\) で割って　←性質２ 
例31
　両辺に \(2\) を加えると　←性質１
　両辺を負の数 \(-4\) で割って　←性質３

p.38 練習35$${\small (1)}~x>2$$$${\small (2)}~x≧-5$$$${\small (3)}~x≧ \frac{6}{7}$$$${\small (4)}~x<0$$$${\small (5)}~x<-\frac{4}{3}$$$${\small (6)}~x≧1$$→ １次不等式の解

p.42 深める$${\small (1)}~x>\frac{\,b\,}{\,a\,}$$$${\small (2)}~x<\frac{\,b\,}{\,a\,}$$

p.43 練習36$${\small (1)}~-1<x≦5$$$${\small (2)}~x≦-\frac{7}{3}$$\({\small (3)}~\)解なし

p.43 練習37$$~~~1<x≦ \frac{7}{4}$$→ 連立不等式の解

p.44 練習38　\(8\) 個

p.44 練習39　\(1000\) ｍ以上
→ 不等式の文章問題

p.45 練習40$${\small (1)}~x=\pm4$$$${\small (2)}~-2<x<2$$$${\small (3)}~x≦-5~,~5≦x$$

p.45 練習41$${\small (1)}~x=2~,~ \frac{2}{3}$$$${\small (2)}~-1≦x≦5$$$${\small (3)}~x<-1~,~0<x$$→ 絶対値を含む方程式と不等式

p.46 研究 練習1$${\small (1)}~x=\frac{1}{2}$$$${\small (2)}~x<1$$$${\small (3)}~x>1$$→ 場合分けの必要な絶対値を含む方程式と不等式