第2章 空間のベクトル

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版数学C 第1章 平面のベクトル
数研出版数学C 第2章 空間のベクトル
数研出版数学C 第3章 複素数平面
数研出版数学C 第4章 式と曲線
第2章 空間のベクトル
\(~~~{\rm M}(0~,~b~,~c)\)
\(~~~{\rm N}(a~,~0~,~c)\)
解法のPoint|平面に下ろした交点の座標
\(~~~{\rm M}(0~,~-3~,~4)\)
\(~~~{\rm N}(2~,~0~,~4)\)
解法のPoint|平面に下ろした交点の座標
\({\small (2)}~{\rm B}(2~,~-4~,~-3)\)
\({\small (3)}~{\rm C}(-2~,~-4~,~-3)\)
解法のPoint|平面・軸・原点に対称な点の座標
\({\small (2)}~(1~,~-2~,~3)\)
\({\small (3)}~(-1~,~2~,~-3)\)
\({\small (4)}~(-1~,~-2~,~3)\)
解法のPoint|平面・軸・原点に対称な点の座標
\({\rm AB}=\sqrt{1^2+1^2+(-2)^2}=\sqrt{6}\)
\({\rm BC}=\sqrt{1^2+(-2)^2+1^2}=\sqrt{6}\)
\({\rm CA}=\sqrt{(-2)^2+1^2+1^2}=\sqrt{6}\)
よって、\({\rm AB=BC=CA}\) となり、\(\triangle {\rm ABC}\) は正三角形である [終]
解法のPoint|空間の3点がつくる三角形
解法のPoint|空間の2点間の距離
\({\small (2)}~-\overrightarrow{a}-\overrightarrow{b}\)
\({\small (3)}~\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\)
解法のPoint|平行六面体とベクトルの加法・減法
解法のPoint|平行六面体とベクトルの実数倍
\({\small (2)}~(2~,~-5~,~5)~,~3\sqrt{6}\)
\({\small (3)}~(2~,~-4~,~6)~,~2\sqrt{14}\)
\({\small (4)}~(-5~,~12~,~-13)~,~13\sqrt{2}\)
解法のPoint|空間ベクトルの成分計算
\({\small (2)}~(4~,~-4~,~2)~,~6\)
\({\small (3)}~(2~,~5~,~1)~,~\sqrt{30}\)
解法のPoint|空間ベクトルの成分計算
解法のPoint|成分計算とベクトルの表し方
解法のPoint|成分計算とベクトルの表し方
\({\small (2)}~(-1~,~5~,~-3)~,~\sqrt{35}\)
\({\small (3)}~(-5~,~-10~,~5)~,~5\sqrt{6}\)
\({\small (4)}~(6~,~5~,~-2)~,~\sqrt{65}\)
解法のPoint|空間の点をベクトルの成分で表す
\( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c}~,~\overrightarrow{d}~,~\overrightarrow{e}~,~\overrightarrow{f}~,~\overrightarrow{g}~,~\overrightarrow{h} \)
とおくと、
平行六面体 \( {\rm ABCD-EFGH} \) より、
下面 \( {\rm ABCD} \) は平行四辺形なので、
\( \overrightarrow{\rm AB}=\overrightarrow{\rm DC} \)
\( \overrightarrow{b}-\overrightarrow{a}=\overrightarrow{c}-\overrightarrow{d} \)
よって、
\( \overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d}~\cdots~{\small [\,1\,]} \)
また、
\( \overrightarrow{\rm AE}=\overrightarrow{\rm BF}=\overrightarrow{\rm CG}=\overrightarrow{\rm DH} \)
なので、
\( \overrightarrow{e}-\overrightarrow{a}=\overrightarrow{f}-\overrightarrow{b}=\overrightarrow{g}-\overrightarrow{c}=\overrightarrow{h}-\overrightarrow{d}~\cdots~{\small [\,2\,]} \)
ここで、対角線 \( {\rm AG} \) の中点は、
\( {\small [\,2\,]} \) より \( \overrightarrow{g}=\overrightarrow{c}+\overrightarrow{e}-\overrightarrow{a} \) なので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{g}\,}{\,2\,}&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{c}+\overrightarrow{e}\,}{\,2\,}\end{eqnarray}\)
また、対角線 \( {\rm CE} \) の中点は、
\( \displaystyle \frac{\,\overrightarrow{c}+\overrightarrow{e}\,}{\,2\,} \)
また、対角線 \( {\rm BH} \) の中点は、
\( {\small [\,2\,]} \) より \( \overrightarrow{h}=\overrightarrow{d}+\overrightarrow{e}-\overrightarrow{a} \) なので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{h}\,}{\,2\,}&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{d}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}\end{eqnarray}\)
また、対角線 \( {\rm DF} \) の中点は、
\( {\small [\,2\,]} \) より \( \overrightarrow{f}=\overrightarrow{b}+\overrightarrow{e}-\overrightarrow{a} \) なので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{d}+\overrightarrow{f}\,}{\,2\,}&=&\displaystyle \frac{\,\overrightarrow{d}+\overrightarrow{b}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{d}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}\end{eqnarray}\)
\( {\small [\,1\,]} \) より \( \overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d} \) なので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{c}+\overrightarrow{e}\,}{\,2\,}&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{d}+\overrightarrow{e}-\overrightarrow{a}\,}{\,2\,}\end{eqnarray}\)
したがって、\( 4 \) つの対角線 \( {\rm AG}~,~{\rm BH}~,~{\rm CE}~,~{\rm DF} \) の中点は一致する [終]
■ この問題の詳しい解説はこちら!
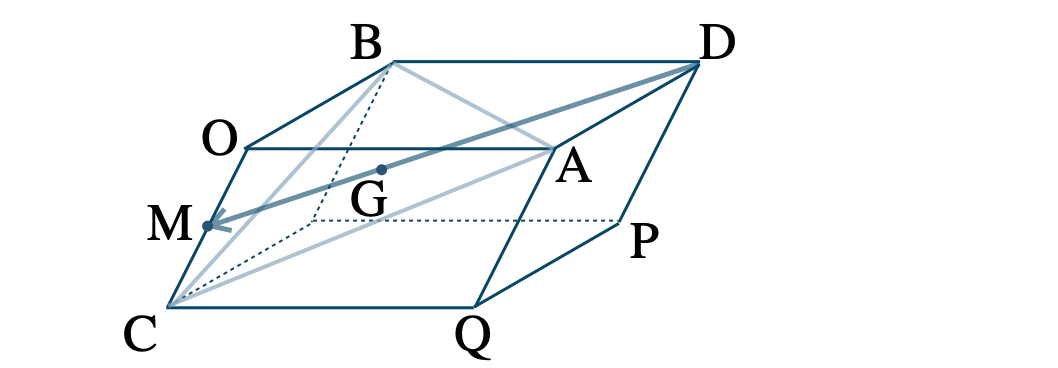
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm OB}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \triangle {\rm ABC} \) の重心が \( {\rm G} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
さらに、\( {\rm M} \) は辺 \( {\rm OC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OC}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DG}&=&\overrightarrow{\rm OG}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{a}-3\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,3\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DM}&=&\overrightarrow{\rm OM}-\overrightarrow{\rm OD}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b})
\\[5pt]~~~&=&-\overrightarrow{a}-\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,5\,]}
\end{eqnarray}\)
\(\small [\,4\,]\)\(\small [\,5\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm DM}&=&\displaystyle \frac{\,1\,}{\,2\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\cdot\displaystyle \frac{\,1\,}{\,3\,}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm DG}\hspace{30pt}(\,∵~ {\small [\,4\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm DM}=\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm DG} \) より、
3点 \( \rm D~,~\rm G~,~\rm M \) は一直線上にある [終]
また、\( {\rm DG}:{\rm DM}=1:\displaystyle \frac{\,3\,}{\,2\,}=2:3 \) より、
\( {\rm DG}:{\rm GM}=2:1 \)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\( \rm AB \perp CD \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm CD}&=&0
\\[5pt]~~~\overrightarrow{\rm AB}\cdot(\overrightarrow{\rm AD}-\overrightarrow{\rm AC})&=&0
\\[5pt]~~~\overrightarrow{x}\cdot(\overrightarrow{z}-\overrightarrow{y})&=&0
\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{z}-\overrightarrow{x}\cdot\overrightarrow{y}&=&0
\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{y}&=&\overrightarrow{z}\cdot\overrightarrow{x}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\( \rm AC \perp BD \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}\cdot\overrightarrow{\rm BD}&=&0
\\[5pt]~~~\overrightarrow{\rm AC}\cdot(\overrightarrow{\rm AD}-\overrightarrow{\rm AB})&=&0
\\[5pt]~~~\overrightarrow{y}\cdot(\overrightarrow{z}-\overrightarrow{x})&=&0
\\[5pt]~~~\overrightarrow{y}\cdot\overrightarrow{z}-\overrightarrow{x}\cdot\overrightarrow{y}&=&0
\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{y}&=&\overrightarrow{y}\cdot\overrightarrow{z}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
ここで、\( \overrightarrow{\rm AD} \) と \( \overrightarrow{\rm BC} \) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}\cdot\overrightarrow{\rm BC}&=&\overrightarrow{\rm AD}\cdot(\overrightarrow{\rm AC}-\overrightarrow{\rm AB})
\\[5pt]~~~&=&\overrightarrow{z}\cdot(\overrightarrow{y}-\overrightarrow{x})
\\[5pt]~~~&=&\overrightarrow{y}\cdot\overrightarrow{z}-\overrightarrow{z}\cdot\overrightarrow{x}
\end{eqnarray}\)
\(\small [\,1\,]\) と \(\small [\,2\,]\) より、
\(\begin{eqnarray}\hspace{35pt}~~~~&=&\overrightarrow{x}\cdot\overrightarrow{y}-\overrightarrow{x}\cdot\overrightarrow{y}
\\[5pt]~~~&=&0
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AD}\neq 0~,~\overrightarrow{\rm BC}\neq 0~,~\overrightarrow{\rm AD}\cdot\overrightarrow{\rm BC}=0 \) より、\( \overrightarrow{\rm AD}\perp\overrightarrow{\rm BC} \) [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~(3~,~-2~,~3)~,~(-5~,~-10~,~19)\)
\({\small (3)}~(4~,~-1~,~1)\)
解法のPoint|座標空間の2点の内分点・外分点・中点
\({\small (4)}~(3~,~-2~,~1)\)
解法のPoint|座標空間の三角形の重心の座標
\({\small (2)}~\left(\displaystyle \frac{\,11\,}{2}~,~-\displaystyle \frac{\,9\,}{2}~,~1\right)\)
解法のPoint|座標空間の2点の内分点・外分点・中点
\({\small (3)}~(3~,~-2~,~-1)\)
解法のPoint|座標空間の三角形の重心の座標
解法のPoint|中心と半径が条件の球面の方程式
\({\small (2)}~x^2+(y-2)^2+(z-2)^2=9\)
解法のPoint|直径の両端が条件の球面の方程式
\({\small (2)}~(x-1)^2+(y+2)^2+z^2=16\)
解法のPoint|中心と半径が条件の球面の方程式
\({\small (3)}~(x-2)^2+(y+1)^2+(z-3)^2=14\)
解法のPoint|直径の両端が条件の球面の方程式
\((x+3)^2+(y-1)^2=9~,~z=0\)
\(yz\) 平面
\((y-1)^2+(z-2)^2=4~,~x=0\)
\(zx\) 平面
\((x+3)^2+(z-2)^2=12~,~y=0\)
解法のPoint|球が座標平面で切り取られる円
\(x\) 軸との交点\(~(3~,~0~,~0)\)
\(y\) 軸との交点\(~\left(0~,~-\displaystyle \frac{3}{\,4\,}~,~0\right)\)
\(z\) 軸との交点\(~~~\left(0~,~0~,~-\displaystyle \frac{\,3\,}{2}\right)\)
解法のPoint|座標空間の平面の方程式
問題
\( \overrightarrow{\rm BC}=\overrightarrow{a}-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}-\overrightarrow{c} \)
■ この問題の詳しい解説はこちら!
\( \cos\gamma=\displaystyle \frac{\,2\,}{\,3\,} \)
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~\overrightarrow{c}&=&(2~,~0~,~2)-(1~,~2~,~3)
\\[3pt]~~~&=&(1~,~-2~,~-1)
\end{eqnarray}\)
\( \overrightarrow{a} \) と \( \overrightarrow{c} \) の内積を計算すると、
\(\begin{eqnarray}~~~\overrightarrow{a}\cdot\overrightarrow{c}&=&2\cdot1+0\cdot(-2)+2\cdot(-1)
\\[3pt]~~~&=&2+0-2
\\[3pt]~~~&=&0
\end{eqnarray}\)
\( \overrightarrow{a}\cdot\overrightarrow{c}=0 \) より、\( \overrightarrow{c} \) は \( \overrightarrow{a} \) に垂直である
\({\small (2)}~\)
\(\begin{eqnarray}~~~\overrightarrow{d}&=&(-\sqrt{3}~,~-\sqrt{3}~,~\sqrt{3})~,~\\[3pt]~~~&&~(\sqrt{3}~,~\sqrt{3}~,~-\sqrt{3})\end{eqnarray}\)
■ この問題の詳しい解説はこちら!
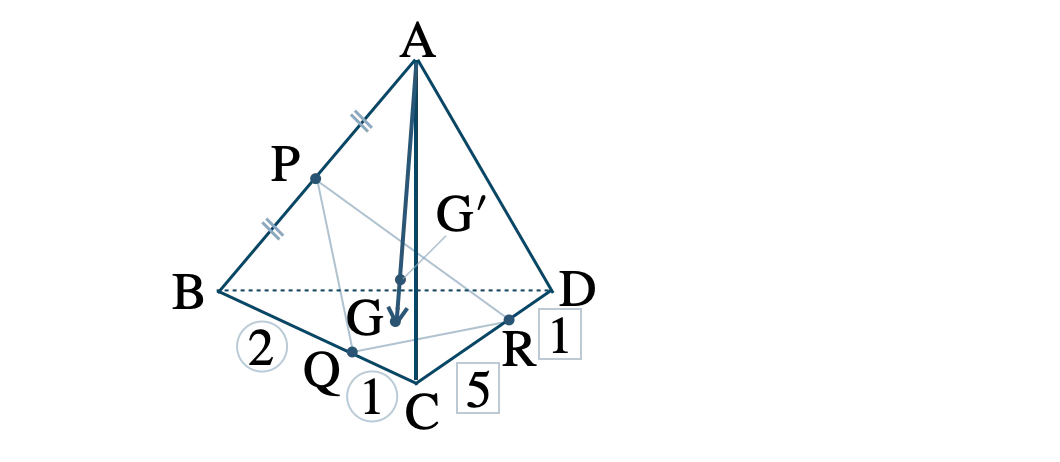
\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\overrightarrow{\rm AC}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{c} \) とおくと、
\( \triangle {\rm BCD} \) の重心を \( {\rm G} \) とすると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\displaystyle \frac{\,\overrightarrow{\rm AB}+\overrightarrow{\rm AC}+\overrightarrow{\rm AD}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
次に、各点の位置ベクトルを求める。
\( {\rm AP}={\rm PB} \) より、点 \( {\rm P} \) は辺 \( {\rm AB} \) の中点なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AB}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}
\end{eqnarray}\)
\( {\rm BQ}=2{\rm QC} \) より、点 \( {\rm Q} \) は辺 \( {\rm BC} \) を \( 2:1 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&\overrightarrow{\rm AB}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}(\overrightarrow{b}-\overrightarrow{a})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}
\end{eqnarray}\)
\( {\rm CR}=5{\rm RD} \) より、点 \( {\rm R} \) は辺 \( {\rm CD} \) を \( 5:1 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AR}&=&\overrightarrow{\rm AC}+\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{\rm CD}
\\[5pt]~~~&=&\overrightarrow{b}+\displaystyle \frac{\,5\,}{\,6\,}(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{c}
\end{eqnarray}\)
\( \triangle {\rm PQR} \) の重心を \( {\rm G’} \) とすると、
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{a}+\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,18\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\(\small [\,1\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG’}&=&\displaystyle \frac{\,5\,}{\,18\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,18\,}\cdot 3\cdot\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{\rm AG}\hspace{30pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AG’}=\displaystyle \frac{\,5\,}{\,6\,}\overrightarrow{\rm AG} \) より、
3点 \( {\rm A}~,~{\rm G’}~,~{\rm G} \)(頂点A,\( \triangle {\rm PQR} \) の重心および \( \triangle {\rm BCD} \) の重心)は一直線上にある [終]
■ この問題の詳しい解説はこちら!
\( 2:1 \)
■ この問題の詳しい解説はこちら!
解法のPoint|中心と通る点が条件の球面の方程式
\({\small (2)}~\)
\( (x-1)^2+(y-1)^2+(z-1)^2=1 \)
\( (x-3)^2+(y-3)^2+(z-3)^2=9 \)
解法のPoint|座標平面に接する球面の方程式
演習問題 空間のベクトル
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OC}+\overrightarrow{\rm OD}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{\left(\,\begin{array}{c}5\\[2pt]1\\[2pt]8\end{array}\,\right)+\left(\,\begin{array}{c}3\\[2pt]-3\\[2pt]6\end{array}\,\right)\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\,\begin{array}{c}8\\[2pt]-2\\[2pt]14\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}4\\[2pt]-1\\[2pt]7\end{array}\,\right)\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}&=&\overrightarrow{\rm OM}-\overrightarrow{\rm OB}
\\[5pt]~~~&=&\left(\,\begin{array}{c}4\\[2pt]-1\\[2pt]7\end{array}\,\right)-\left(\,\begin{array}{c}1\\[2pt]3\\[2pt]2\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}4-1\\[2pt]-1-3\\[2pt]7-2\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}3\\[2pt]-4\\[2pt]5\end{array}\,\right)\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm CD}&=&\overrightarrow{\rm OD}-\overrightarrow{\rm OC}
\\[5pt]~~~&=&\left(\,\begin{array}{c}3\\[2pt]-3\\[2pt]6\end{array}\,\right)-\left(\,\begin{array}{c}5\\[2pt]1\\[2pt]8\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}3-5\\[2pt]-3-1\\[2pt]6-8\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}-2\\[2pt]-4\\[2pt]-2\end{array}\,\right)\end{eqnarray}\)
ここで、\(\overrightarrow{\rm BM}\) と \(\overrightarrow{\rm CD}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm CD}&=&3\cdot(-2)+(-4)\cdot(-4)+5\cdot(-2)
\\[3pt]~~~&=&-6+16-10
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm BM}\neq\overrightarrow{0}~,~\overrightarrow{\rm CD}\neq\overrightarrow{0}\) より、\( {\rm BM}\perp{\rm CD} \)
\({\small (2)}~10\sqrt{3}\)
\({\small (3)}~\)\(\overrightarrow{\rm AB}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&\overrightarrow{\rm OB}-\overrightarrow{\rm OA}
\\[5pt]~~~&=&\left(\,\begin{array}{c}1\\[2pt]3\\[2pt]2\end{array}\,\right)-\left(\,\begin{array}{c}8\\[2pt]2\\[2pt]-3\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}1-8\\[2pt]3-2\\[2pt]2+3\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}-7\\[2pt]1\\[2pt]5\end{array}\,\right)\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm BC}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BC}&=&(-7)\cdot4+1\cdot(-2)+5\cdot6
\\[3pt]~~~&=&-28-2+30
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AB}\neq\overrightarrow{0}~,~\overrightarrow{\rm BC}\neq\overrightarrow{0}\) より、\( {\rm AB}\perp{\rm BC} \)
また、\(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm BD}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BD}&=&(-7)\cdot2+1\cdot(-6)+5\cdot4
\\[3pt]~~~&=&-14-6+20
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AB}\neq\overrightarrow{0}~,~\overrightarrow{\rm BD}\neq\overrightarrow{0}\) より、\( {\rm AB}\perp{\rm BD} \)
\({\small (4)}~50\)
■ この問題の詳しい解説はこちら!
\(\overrightarrow{\rm OA}=\left(\begin{array}{c}2\\0\\0\end{array}\right)~,~\overrightarrow{\rm OB}=\left(\begin{array}{c}0\\1\\0\end{array}\right)~,~\overrightarrow{\rm OC}=\left(\begin{array}{c}0\\0\\2\end{array}\right)\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&\overrightarrow{\rm OB}-\overrightarrow{\rm OA}
\\[5pt]~~~&=&\left(\begin{array}{c}0\\1\\0\end{array}\right)-\left(\begin{array}{c}2\\0\\0\end{array}\right)
\\[5pt]~~~&=&\left(\begin{array}{c}-2\\1\\0\end{array}\right)\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}&=&\overrightarrow{\rm OC}-\overrightarrow{\rm OA}
\\[5pt]~~~&=&\left(\begin{array}{c}0\\0\\2\end{array}\right)-\left(\begin{array}{c}2\\0\\0\end{array}\right)
\\[5pt]~~~&=&\left(\begin{array}{c}-2\\0\\2\end{array}\right)\end{eqnarray}\)
また、\(\overrightarrow{\rm OH}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}+u\overrightarrow{\rm OC}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OH}&=&s\left(\begin{array}{c}2\\0\\0\end{array}\right)+t\left(\begin{array}{c}0\\1\\0\end{array}\right)+u\left(\begin{array}{c}0\\0\\2\end{array}\right)
\\[5pt]~~~&=&\left(\begin{array}{c}2s\\t\\2u\end{array}\right)\end{eqnarray}\)
\(\overrightarrow{\rm OH}\perp\overrightarrow{\rm AB}\) より、\(\overrightarrow{\rm OH}\cdot\overrightarrow{\rm AB}=0\) となるので、
\(\begin{eqnarray}~~~2s\cdot(-2)+t\cdot1+2u\cdot0&=&0
\\[3pt]~~~-4s+t&=&0
\\[3pt]~~~4s-t&=&0\end{eqnarray}\)
\(\overrightarrow{\rm OH}\perp\overrightarrow{\rm AC}\) より、\(\overrightarrow{\rm OH}\cdot\overrightarrow{\rm AC}=0\) となるので、
\(\begin{eqnarray}~~~2s\cdot(-2)+t\cdot0+2u\cdot2&=&0
\\[3pt]~~~-4s+4u&=&0
\\[3pt]~~~s-u&=&0\end{eqnarray}\)
したがって、\(4s-t=0~,~s-u=0\) が成り立つ
\({\small (2)}~\)\( \left(\,\displaystyle \frac{\,1\,}{\,3\,}~,~\displaystyle \frac{\,2\,}{\,3\,}~,~\displaystyle \frac{\,1\,}{\,3\,}\,\right) \)
\({\small (3)}~\)\( \displaystyle \frac{\,\sqrt{6}\,}{\,3\,} \)
■ この問題の詳しい解説はこちら!
次のページ「第3章 複素数平面」


