1章 ベクトル
それぞれの問題の解説はありませんが、類題の解説はリンク先にありますので参考にしてください。
また、解答は独自で解いたものですので、間違えやタイプミス等がありましたらご連絡ください。

1章 ベクトル
1節 平面上のベクトル
互いに逆ベクトル \(\overrightarrow{b}\) と \(\overrightarrow{e}\)
解法のPoint|ベクトルの大きさと等しいベクトル
解法のPoint|ベクトルの等式の証明方法
\(\begin{eqnarray}~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CA}
\\[3pt]~~~&=&\overrightarrow{\rm AC}+\overrightarrow{\rm CA}
\\[3pt]~~~&=&\overrightarrow{\rm AA}
\\[3pt]~~~&=&\overrightarrow{0}
\end{eqnarray}\)
よって、\(\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CA}=\overrightarrow{0}\) [終]
解法のPoint|ベクトルの等式の証明方法
解法のPoint|ベクトルの式の計算方法
解法のPoint|ベクトルの実数倍の図示
\(\overrightarrow{b}=(2~,~4)~,~|\overrightarrow{b}|=2\sqrt{5}\)
\(\overrightarrow{c}=(-3~,~0)~,~|\overrightarrow{c}|=3\)
\(\overrightarrow{d}=(-4~,~-1)~,~|\overrightarrow{d}|=\sqrt{17}\)
解法のPoint|ベクトルの成分と大きさ
\({\small (2)}~(9~,~-16)\)
\({\small (3)}~(0~,~1)\)
解法のPoint|ベクトルの成分を用いた計算
\({\small (2)}~\left(-\displaystyle\frac{\,\sqrt{5}\,}{\,5\,}~,~\displaystyle\frac{\,2\sqrt{5}\,}{\,5\,}\right)\)
解法のPoint|ベクトルと平行な単位ベクトルの成分
\( \overrightarrow{\rm AC}=(-1~,~2) ~,~|\,\overrightarrow{\rm AC}\,|=\sqrt{5} \)
\( \overrightarrow{\rm BC}=(-4~,~1) ~,~|\,\overrightarrow{\rm BC}\,|=\sqrt{17} \)
解法のPoint|2点の座標とベクトルの成分・大きさ
\({\small (3)}~1\) \({\small (4)}~-1\)
解法のPoint|ベクトルの大きさ・なす角と内積
解法のPoint|正方形における内積
\({\small (3)}~\overrightarrow{a}\cdot\overrightarrow{b}=0\) \({\small (4)}~\overrightarrow{a}\cdot\overrightarrow{b}=-2\sqrt{3}\)
解法のPoint|ベクトルの成分と内積
\({\small (3)}~\theta=90^\circ\) \({\small (4)}~\theta=180^\circ\)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
(左辺)
\(=|\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}+\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\(|\overrightarrow{a}+\overrightarrow{b}|^2=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\) [終]
\({\small (2)}~\)
(左辺)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{b}\cdot\overrightarrow{a}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\((\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
[終]
解法のPoint|ベクトルの等式の証明
Training
\({\small (2)}~\) \( -2\overrightarrow{a} \)
\({\small (3)}~\) \( -\overrightarrow{a}+\overrightarrow{b} \)
\({\small (4)}~\) \( -\overrightarrow{a}-2\overrightarrow{b} \)
解法のPoint|正六角形のベクトルの表し方
\({\small (2)}~\) \( (1~,~-7) \)
\({\small (3)}~\) \( (1~,~3) \)
解法のPoint|ベクトルの成分を用いた計算
\({\small (2)}~\) \( \left(\,\displaystyle \frac{\,1\,}{\,5\sqrt{2}\,}~,~-\displaystyle \frac{\,7\,}{\,5\sqrt{2}\,}\,\right) \)
解法のPoint|ベクトルと平行な単位ベクトルの成分
解法のPoint|ベクトルと平行な単位ベクトルの成分
解法のPoint|成分によるベクトルの分解
解法のPoint|正方形における内積
\({\small (3)}~\) \( \theta=90^{\circ} \) \({\small (4)}~\) \( \theta=45^{\circ} \)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)\(\overrightarrow{a}\) と \(\overrightarrow{b}\) が同じ向き
解法のPoint|ベクトルの大きさ・なす角と内積
2節 ベクトルの応用
解法のPoint|位置ベクトルの内分点・外分点・中点
\({\small (2)}~\overrightarrow{p}=\displaystyle\frac{\,5\overrightarrow{a}+2\overrightarrow{b}\,}{\,7\,}~,~\overrightarrow{q}=\displaystyle\frac{\,5\overrightarrow{a}-2\overrightarrow{b}\,}{\,3\,} \)
解法のPoint|位置ベクトルの内分点・外分点・中点
解法のPoint|重心が一致することの証明(位置ベクトル)
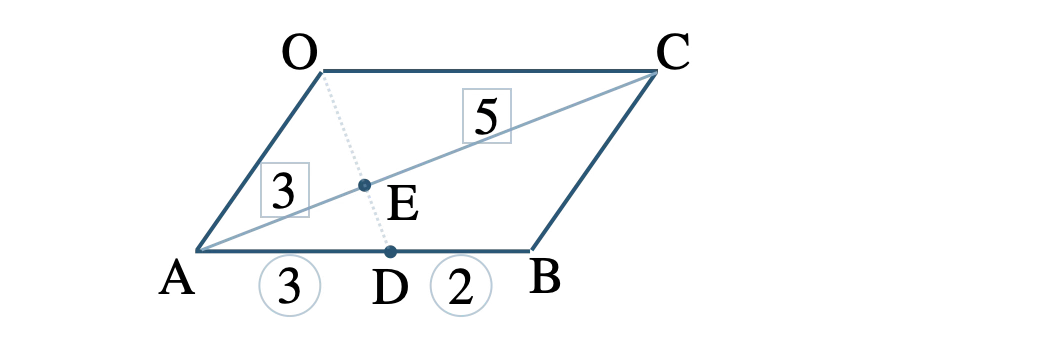
平行四辺形 \({\rm OABC}\) で、\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) とおくと、
\(\overrightarrow{\rm OB}=\overrightarrow{a}+\overrightarrow{c}\)
点 \( \rm D \) は辺 \( \rm AB \) を \(3:2\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}
&=&\displaystyle \frac{\,2{\, \small \times \,}\overrightarrow{\rm OA}+3{\, \small \times \,}\overrightarrow{\rm OB}\,}{\,3+2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{a}+3(\overrightarrow{a}+\overrightarrow{c})\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\overrightarrow{a}+3\overrightarrow{c}\,}{\,5\,}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、点 \( \rm E \) は対角線 \( \rm AC \) を \(3:5\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}
&=&\displaystyle \frac{\,5{\, \small \times \,}\overrightarrow{\rm OA}+3{\, \small \times \,}\overrightarrow{\rm OC}\,}{\,3+5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\overrightarrow{a}+3\overrightarrow{c}\,}{\,8\,}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) を式変形して、\({\small [\,2\,]}\) と比較すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}
&=&\displaystyle \frac{\,5\overrightarrow{a}+3\overrightarrow{c}\,}{\,8\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\overrightarrow{a}+3\overrightarrow{c}\,}{\,8\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,8\,}{\, \small \times \,}\displaystyle \frac{\,5\overrightarrow{a}+3\overrightarrow{c}\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,8\,}\,\overrightarrow{\rm OD} \hspace{20pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、点 \( \rm O~,~E~,~D \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
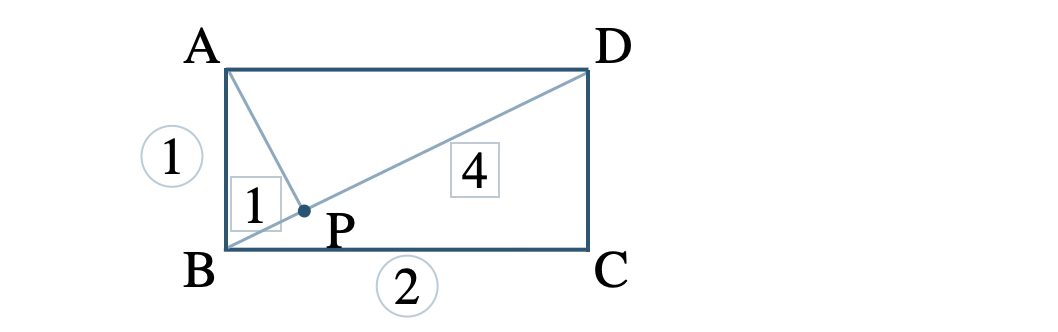
\(\overrightarrow{\rm BA}=\overrightarrow{a}~,~\overrightarrow{\rm BC}=\overrightarrow{c}\) とおくと、
四角形 \({\rm ABCD}\) は長方形より、
\(\overrightarrow{a}\cdot\overrightarrow{c}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\({\rm AB}=1\) より、
\(|\overrightarrow{a}|^2=1~ ~ ~ \cdots {\small [\,2\,]}\)
\({\rm BC}=2\) より、
\(|\overrightarrow{c}|^2=4~ ~ ~ \cdots {\small [\,3\,]}\)
長方形より、\(\overrightarrow{\rm BD}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BD}&=&\overrightarrow{\rm BA}+\overrightarrow{\rm AD}\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{c}\end{eqnarray}\)
点 \({\rm P}\) は対角線 \({\rm BD}\) を \(1:4\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm BP}&=&\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm BD}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\end{eqnarray}\)
よって、\(\overrightarrow{\rm AP}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BP}\\[5pt]~~~&=&-\overrightarrow{a}+\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\\[5pt]~~~&=&\displaystyle \frac{\,-5\overrightarrow{a}+\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\\[5pt]~~~&=&\displaystyle \frac{\,-4\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{\rm BD}\) の内積は、
\({\small [\,1\,]}~,~{\small [\,2\,]}~,~{\small [\,3\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,5\,}(-4\cdot 1+4-0)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AP}\neq\overrightarrow{0}~,~\overrightarrow{\rm BD}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AP}\perp \overrightarrow{\rm BD}\)
したがって、\({\rm AP}\perp {\rm BD}\) [終]
■ この問題の詳しい解説はこちら!
x=2+t \\ y=-3+2t \\
\end{array}\right.~,~2x-y-7=0 \)
\({\small (2)}~\left\{~\begin{array}{l}
x=4-3t \\ y=2t \\
\end{array}\right.~,~2x+3y-8=0 \)
解法のPoint|方向ベクトルと直線の媒介変数表示
\( t=0 \) のとき、点\( {\rm A} \)
\( t=\displaystyle\frac{\,1\,}{\,3\,} \) のとき、線分\( {\rm AB} \) を \( 1:2 \) に内分する点
\( t=\displaystyle\frac{\,1\,}{\,2\,} \) のとき、線分\( {\rm AB} \) の中点
\( t=2 \) のとき、線分\( {\rm AB} \) を \( 2:1 \) に外分する点
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)中心 \(\displaystyle \frac{\,\overrightarrow{a}\,}{\,3\,}\)、半径 \(2\) の円
解法のPoint|中心と半径が条件の円のベクトル方程式
Training
\({\small (2)}~\) \( \displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,} \)
\({\small (3)}~\) \( \displaystyle \frac{\,-\overrightarrow{c}+4\overrightarrow{a}\,}{\,3\,} \)
解法のPoint|位置ベクトルの内分点・外分点・中点
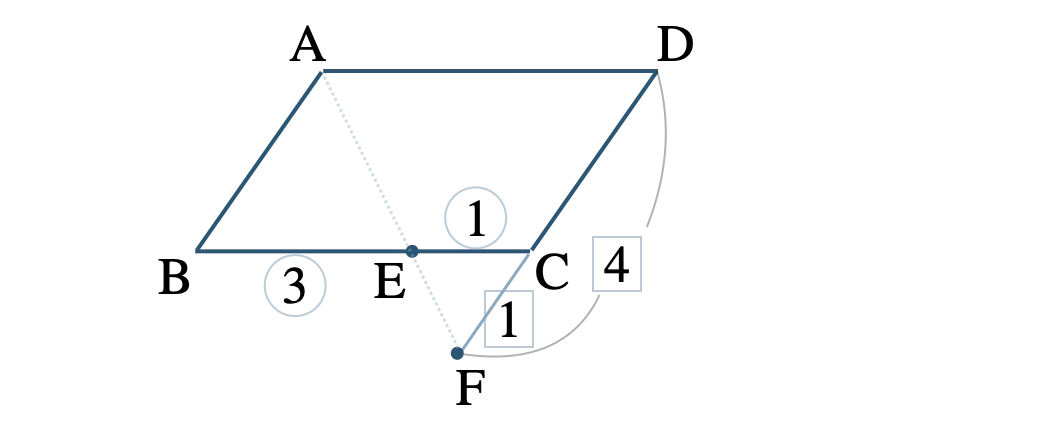
平行四辺形 \({\rm ABCD}\) で、\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とおくと、
\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}\)
点 \( \rm E \) は辺 \( \rm BC \) を \(3:1\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AE}
&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{\rm AB}+3{\, \small \times \,}\overrightarrow{\rm AC}\,}{\,3+1\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+3(\overrightarrow{b}+\overrightarrow{d})\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{d}\,}{\,4\,}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、点 \( \rm F \) は辺 \( \rm CD \) を \(1:4\) に外分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF}
&=&\displaystyle \frac{\,-4{\, \small \times \,}\overrightarrow{\rm AC}+1{\, \small \times \,}\overrightarrow{\rm AD}\,}{\,1-4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-4(\overrightarrow{b}+\overrightarrow{d})+\overrightarrow{d}\,}{\,-3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-4\overrightarrow{b}-3\overrightarrow{d}\,}{\,-3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{d}\,}{\,3\,}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) を式変形して、\({\small [\,2\,]}\) と比較すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF}
&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{d}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,4\,}{\, \small \times \,}\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{d}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}{\, \small \times \,}\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{d}\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,3\,}\,\overrightarrow{\rm AE} \hspace{20pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、点 \( \rm A~,~E~,~F \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( \left\{\begin{array}{l}x=-t\\y=-2-4t\end{array}\right.~,~y=4x-2 \)
解法のPoint|方向ベクトルと直線の媒介変数表示
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( \sqrt{2}\,x-y=0 \)
解法のPoint|法線ベクトルと直線の方程式
\({\small (2)}~\) 中心 \( -\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{a} \)、半径 \( 3 \) の円
解法のPoint|中心と半径が条件の円のベクトル方程式
3節 空間におけるベクトル
逆ベクトル \(\overrightarrow{\rm CA}~,~\overrightarrow{\rm GE}\)
\(\begin{eqnarray}~~~&=&\overrightarrow{\rm AF}-\overrightarrow{\rm BC}
\\[3pt]~~~&=&\overrightarrow{\rm AF}-\overrightarrow{\rm AD}
\\[3pt]~~~&=&\overrightarrow{\rm DF}
\end{eqnarray}\)
\({\small (2)}~\)左辺
\(\begin{eqnarray}~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AF}
\\[3pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CG}
\\[3pt]~~~&=&\overrightarrow{\rm AC}+\overrightarrow{\rm CG}
\\[3pt]~~~&=&\overrightarrow{\rm AG}
\end{eqnarray}\)
\({\small (2)}~\overrightarrow{a}-\overrightarrow{b}\)
\({\small (3)}~-\overrightarrow{a}+\overrightarrow{c}\)
\({\small (4)}~-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
解法のPoint|平行六面体とベクトルの加法・減法
解法のPoint|成分計算とベクトルの表し方
解法のPoint|空間の点をベクトルの成分で表す
\({\small (3)}~-8\) \({\small (4)}~4\)
解法のPoint|空間ベクトルの内積計算
■ この問題の詳しい解説はこちら!
解法のPoint|空間の位置ベクトルと内分点・外分点・中点
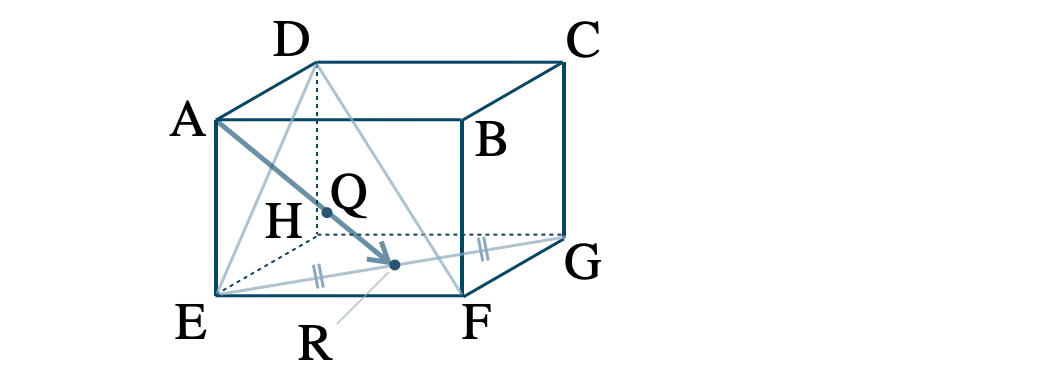
\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\overrightarrow{\rm AD}=\overrightarrow{b}~,~\overrightarrow{\rm AE}=\overrightarrow{c} \) とおくと、
直方体より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BF}=\overrightarrow{a}+\overrightarrow{c}
\\[5pt]~~~\overrightarrow{\rm AG}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AE}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}
\end{eqnarray}\)
\( \triangle {\rm DEF} \) の重心が \( {\rm Q} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&\displaystyle \frac{\,\overrightarrow{\rm AD}+\overrightarrow{\rm AE}+\overrightarrow{\rm AF}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{a}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( {\rm R} \) は線分 \( {\rm GE} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AR}&=&\displaystyle \frac{\,\overrightarrow{\rm AG}+\overrightarrow{\rm AE}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\(\small [\,1\,]\)\(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AR}&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\cdot\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm AQ}\hspace{30pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AR}=\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm AQ} \) より、
3点 \( \rm A~,~\rm Q~,~\rm R \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
② 平行六面体であっても、\(\overrightarrow{\rm AR}\) や \(\overrightarrow{\rm AQ}\) は同じ様に表されるので、3点 \({\rm A~,~Q~,~R}\) は一直線上にある。
正四面体の1辺の長さを \(a\) とすると、
\(|\overrightarrow{x}|=|\overrightarrow{y}|=|\overrightarrow{z}|=a\)
\(|{\rm BC}|=a\) より、
\(\begin{eqnarray}~~~|\overrightarrow{\rm BC}|^2&=&a^2\\[5pt]~~~|\overrightarrow{y}-\overrightarrow{x}|^2&=&a^2\\[5pt]~~~|\overrightarrow{x}|^2-2\overrightarrow{x}\cdot\overrightarrow{y}+|\overrightarrow{y}|^2&=&a^2\\[5pt]~~~a^2-2\overrightarrow{x}\cdot\overrightarrow{y}+a^2&=&a^2\\[5pt]~~~\overrightarrow{x}\cdot\overrightarrow{y}&=&\displaystyle \frac{\,a^2\,}{\,2\,}\end{eqnarray}\)
同様に、\(|{\rm CD}|=|{\rm BD}|=a\) より、
\(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}=\displaystyle \frac{\,a^2\,}{\,2\,}\)
よって、
\(\overrightarrow{x}\cdot\overrightarrow{y}=\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}~ ~ ~ \cdots {\small [\,1\,]}\)
\(\triangle{\rm BCD}\) の重心 \({\rm G}\) の位置ベクトルは、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{\rm AB}+\overrightarrow{\rm AC}+\overrightarrow{\rm AD})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm AG} \) と \( \overrightarrow{\rm BC} \) の内積は、
正四面体より \(|\overrightarrow{x}|=|\overrightarrow{y}|\) かつ \({\small [\,1\,]}\) より \(\overrightarrow{y}\cdot\overrightarrow{z}=\overrightarrow{z}\cdot\overrightarrow{x}\) なので、
\(\begin{eqnarray}\hspace{35pt}&=&\displaystyle \frac{\,1\,}{\,3\,}(0+0)\\[5pt]~~~&=&0\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AG}\neq 0~,~\overrightarrow{\rm BC}\neq 0~,~\overrightarrow{\rm AG}\cdot\overrightarrow{\rm BC}=0 \) より、\( \overrightarrow{\rm AG}\perp\overrightarrow{\rm BC} \) [終]
■ この問題の詳しい解説はこちら!
Training
\( |\,\overrightarrow{\rm AB}\,|=\sqrt{61} \)
解法のPoint|空間の点をベクトルの成分で表す
解法のPoint|成分表示の空間ベクトルのなす角
■ この問題の詳しい解説はこちら!
解法のPoint|空間の位置ベクトルと内分点・外分点・中点
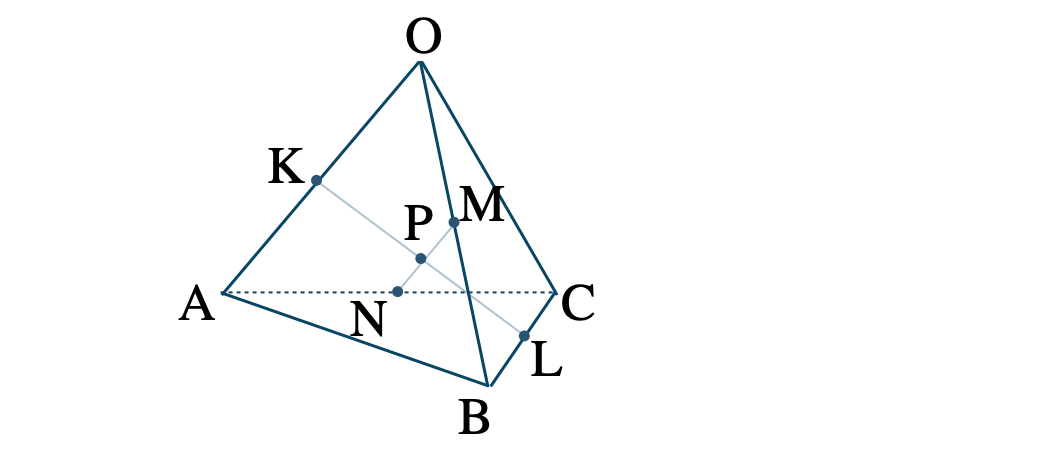
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\( {\rm K} \) は辺 \( {\rm OA} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OK}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\( {\rm L} \) は辺 \( {\rm BC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OL}&=&\overrightarrow{\rm OB}+\overrightarrow{\rm BL}
\\[5pt]~~~&=&\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\( {\rm M} \) は辺 \( {\rm OB} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
\( {\rm N} \) は辺 \( {\rm AC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm ON}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm AN}
\\[5pt]~~~&=&\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AC}
\\[5pt]~~~&=&\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{a})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\( {\rm P} \) は線分 \( {\rm KL} \) の中点より、\(\small [\,1\,]\)\(\small [\,2\,]\) から、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,\overrightarrow{\rm OK}+\overrightarrow{\rm OL}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{b}+\overrightarrow{c})\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,5\,]}
\end{eqnarray}\)
\(\small [\,3\,]\)\(\small [\,5\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm MP}&=&\overrightarrow{\rm OP}-\overrightarrow{\rm OM}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}-\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,6\,]}
\end{eqnarray}\)
\(\small [\,3\,]\)\(\small [\,4\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm MN}&=&\overrightarrow{\rm ON}-\overrightarrow{\rm OM}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{c})-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,7\,]}
\end{eqnarray}\)
\(\small [\,6\,]\)\(\small [\,7\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm MN}&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&2\cdot\displaystyle \frac{\,1\,}{\,4\,}(\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&2\overrightarrow{\rm MP}\hspace{30pt}(\,∵~ {\small [\,6\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm MN}=2\overrightarrow{\rm MP} \) より、
3点 \( \rm M~,~\rm P~,~\rm N \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
解法のPoint|直径の両端が条件の球面の方程式
\({\small (2)}~\) \( x^2+(y+3)^2+(z-4)^2=9 \)
解法のPoint|球が平面と交わってできる円の方程式
\(\begin{eqnarray}~~~1&=&kt~~~\cdots~{\small [\,1\,]}\\[3pt]~~~k&=&3t~~~\cdots~{\small [\,2\,]}\\[3pt]~~~2&=&4t~~~\cdots~{\small [\,3\,]}\end{eqnarray}\)
\( {\small [\,3\,]} \) より \( t=\displaystyle\frac{\,1\,}{\,2\,} \)
\( {\small [\,1\,]} \) に代入すると \( k=2 \)
\( {\small [\,2\,]} \) に代入すると \( k=\displaystyle\frac{\,3\,}{\,2\,} \)
\( k \) の値が一致しないので、\( \overrightarrow{a}=t\overrightarrow{b} \) を満たす実数 \( t \) は存在しない
したがって、\( \overrightarrow{a} \) と \( \overrightarrow{b} \) は平行にならない
Level Up
\({\small (2)}~\)\( t_1=2 \) のとき、最小値 \( 3 \)
\({\small (3)}~\) \((\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}\) を計算すると、
\(\begin{eqnarray}~~~(\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}&=&\overrightarrow{a}\cdot\overrightarrow{b}+t_1\overrightarrow{b}\cdot\overrightarrow{b}
\\[3pt]~~~&=&\overrightarrow{a}\cdot\overrightarrow{b}+t_1|\,\overrightarrow{b}\,|^2\end{eqnarray}\)
\( \overrightarrow{a}\cdot\overrightarrow{b}=-8~,~t_1=2~,~|\,\overrightarrow{b}\,|=2 \) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&-8+2\cdot 2^2
\\[3pt]~~~&=&-8+8
\\[3pt]~~~&=&0\end{eqnarray}\)
よって、\((\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}=0\) より、\(\overrightarrow{a}+t_1\overrightarrow{b}\) と \(\overrightarrow{b}\) は垂直である
■ この問題の詳しい解説はこちら!
\( \overrightarrow{a} \) と \( \overrightarrow{b} \) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{a}\cdot\overrightarrow{b}&=&|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\cos\theta
\\[5pt]~~~\cos\theta&=&\displaystyle\frac{\,\overrightarrow{a}\cdot\overrightarrow{b}\,}{\,|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\,}~~~\cdots{\small [\,1\,]}
\end{eqnarray}\)
\( \triangle{\rm OAB} \) の面積 \( S \) は、
\(\begin{eqnarray}~~~S=\displaystyle\frac{\,1\,}{\,2\,}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\sin\theta
\end{eqnarray}\)
ここで、\( \sin\theta>0 \) より、\( \sin\theta=\sqrt{1-\cos^2\theta} \) であるから、
\(\begin{eqnarray}~~~~~&=&\displaystyle\frac{\,1\,}{\,2\,}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\cdot\sqrt{1-\cos^2\theta}\end{eqnarray}\)
\({\small [\,1\,]}\) を代入すると、
\(\begin{eqnarray}~~~~~&=&\displaystyle\frac{\,1\,}{\,2\,}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\cdot\sqrt{1-\frac{\,(\overrightarrow{a}\cdot\overrightarrow{b})^2\,}{\,|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2\,}}
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}\sqrt{|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2\left\{1-\frac{\,(\overrightarrow{a}\cdot\overrightarrow{b})^2\,}{\,|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2\,}\right\}}
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}\sqrt{|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}
\end{eqnarray}\)
したがって、
\( S=\displaystyle\frac{\,1\,}{\,2\,}\sqrt{|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2} \)
[終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~17\)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( {\rm BQ}:{\rm QC}=5:4~,~{\rm AP}:{\rm PQ}=3:1 \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) 点 \({\rm Q}\) は線分 \({\rm BC}\) を \( 3:2 \) に内分する点
点 \({\rm P}\) は線分 \({\rm AQ}\) を \( 5:1 \) に内分する点
\({\small (3)}~\) \( 1:2:3 \)
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=| \overrightarrow{b} |^2+| \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \overrightarrow{\rm AM} \) は中点の公式より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AM}&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,}
\end{eqnarray}\)
これより、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{b}+\overrightarrow{c} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{b}+\overrightarrow{c})\cdot(\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\end{eqnarray}\)
次に、\( \overrightarrow{\rm BM}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~| \overrightarrow{\rm BM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{c}-\overrightarrow{b}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{c}-\overrightarrow{b} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{c}-\overrightarrow{b})\cdot(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\end{eqnarray}\)
以上より、右辺は、
\\[5pt]~~~&=&2 \cdot \displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2+ | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\,( 2\,| \overrightarrow{b} |^2 + 2\,| \overrightarrow{c} |^2 )
\\[5pt]~~~&=&| \overrightarrow{b} |^2 + | \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
よって、\(\small [\,1\,]\) と \(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=2( | \overrightarrow{\rm AM} |^2+| \overrightarrow{\rm BM} |^2 )
\end{eqnarray}\)
したがって、\({\rm AB^2+AC^2=2(AM^2+BM^2)}\) [終]
■ この問題の詳しい解説はこちら!
直線 \( 3x+y+2=0 \) では \( (3~,~1) \)
\({\small (2)}~\) \( \theta=45^{\circ} \)
解法のPoint|法線ベクトルと2直線のなす角
\({\small (2)}~\)\(\overrightarrow{\rm AD}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\overrightarrow{\rm OD}-\overrightarrow{\rm OA}
\\[5pt]~~~&=&\left(\,\begin{array}{c}-2\\[2pt]4\\[2pt]2\end{array}\,\right)-\left(\,\begin{array}{c}-1\\[2pt]1\\[2pt]0\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}-2+1\\[2pt]4-1\\[2pt]2-0\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}-1\\[2pt]3\\[2pt]2\end{array}\,\right)\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AD}\) と \(\overrightarrow{\rm AB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}\cdot\overrightarrow{\rm AB}&=&(-1)\cdot2+3\cdot0+2\cdot1
\\[3pt]~~~&=&-2+0+2
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AD}\neq\overrightarrow{0}~,~\overrightarrow{\rm AB}\neq\overrightarrow{0}\) より、\( {\rm AD}\perp{\rm AB} \)
また、\(\overrightarrow{\rm AD}\) と \(\overrightarrow{\rm AC}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}\cdot\overrightarrow{\rm AC}&=&(-1)\cdot1+3\cdot3+2\cdot(-4)
\\[3pt]~~~&=&-1+9-8
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AD}\neq\overrightarrow{0}~,~\overrightarrow{\rm AC}\neq\overrightarrow{0}\) より、\( {\rm AD}\perp{\rm AC} \)
\({\rm AD}\perp{\rm AB}~,~{\rm AD}\perp{\rm AC}\) より、直線 \( \rm AD \) は平面 \( \rm ABC \) に垂直である
\({\small (3)}~\)\( 7 \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( {\rm C}(-1~,~4~,~-3) \)
\({\small (3)}~\) \( {\rm D}(-1~,~4~,~3) \)
解法のPoint|平面・軸・原点に対称な点の座標
\({\small (4)}~\) \( {\rm E}(1~,~8~,~-3) \)
解法のPoint|座標空間の点を通る平面の方程式
解法のPoint|座標平面に接する球面の方程式
\({\small (2)}~\) 中心 \( (-2~,~-1~,~1) \)、半径 \( 3 \)
解法のPoint|球が平面と交わってできる円の方程式




