1章 ベクトル
それぞれの問題の解説はありませんが、類題の解説はリンク先にありますので参考にしてください。
また、解答は独自で解いたものですので、間違えやタイプミス等がありましたらご連絡ください。
東京書籍:Advanced数学Ⅲ[701]の解答はこちらから↓



文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学C 1章 ベクトル
Advanced数学C 2章 平面上の曲線
Advanced数学C 3章 複素数平面
1章 ベクトル
1節 平面上のベクトル
互いに逆ベクトル \(\overrightarrow{b}\) と \(\overrightarrow{e}\)
解法のPoint|ベクトルの大きさと等しいベクトル
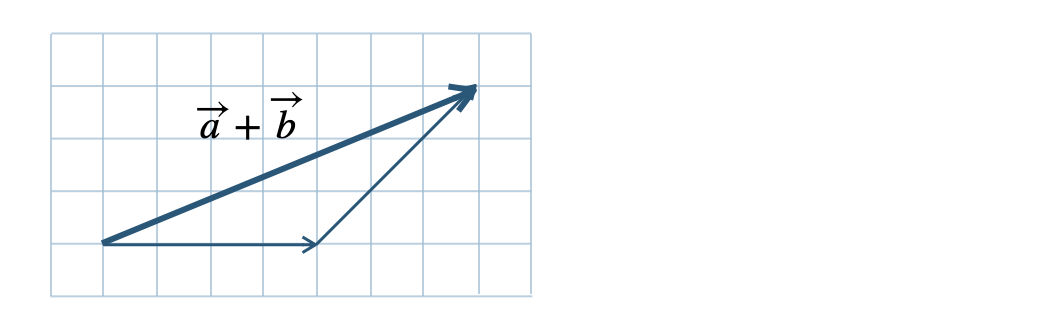
\(\begin{split}&(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\\[3pt]~~=~&(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+\overrightarrow{\rm CD}\\[3pt]~~=~&\overrightarrow{\rm AC}+\overrightarrow{\rm CD}\\[3pt]~~=~&\overrightarrow{\rm AD}\end{split}\)
また、
\(\begin{split}&\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\\[3pt]~~=~&\overrightarrow{\rm AB}+(\overrightarrow{\rm BC}+\overrightarrow{\rm CD})\\[3pt]~~=~&\overrightarrow{\rm AB}+\overrightarrow{\rm BD}\\[3pt]~~=~&\overrightarrow{\rm AD}\end{split}\)
したがって、
\(~~~(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\)
[終]
解法のPoint|ベクトルの等式の証明方法
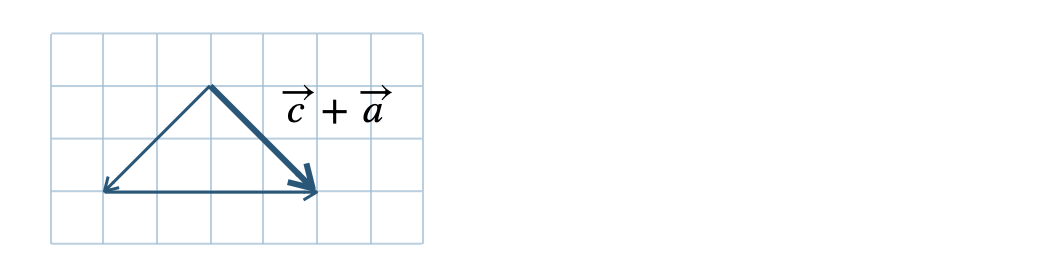
\(\begin{split}&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CA}\\[3pt]~~=~&(\overrightarrow{\rm AB}+\overrightarrow{\rm BC})+\overrightarrow{\rm CA}\\[3pt]~~=~&\overrightarrow{\rm AC}+\overrightarrow{\rm CA}\\[3pt]~~=~&\overrightarrow{\rm AA}\\[3pt]~~=~&\overrightarrow{0}\end{split}\)
[終]
解法のPoint|ベクトルの等式の証明方法
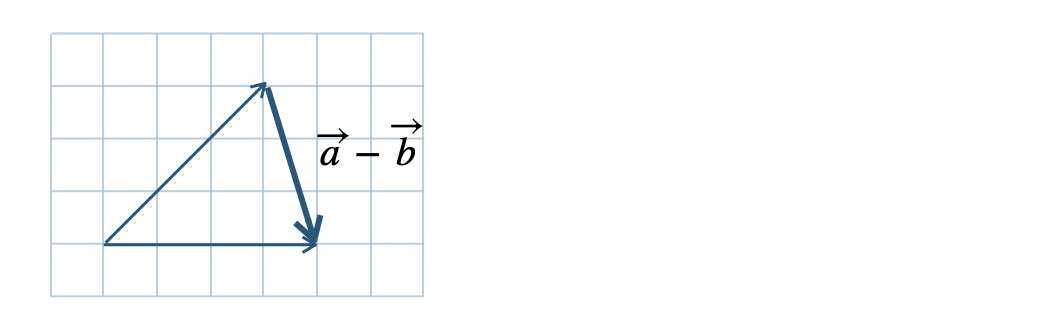
解法のPoint|ベクトルの差の表し方
\(~~~\overrightarrow{\rm A’B’}=k\overrightarrow{\rm AB}=k\overrightarrow{a}\)
\(~~~\overrightarrow{\rm B’C’}=k\overrightarrow{\rm BC}=k\overrightarrow{b}\)
\(~~~\overrightarrow{\rm A’C’}=k\overrightarrow{\rm AC}=k(\overrightarrow{a}+\overrightarrow{b})\)
これより、
\(\begin{split}&k(\overrightarrow{a}+\overrightarrow{b})\\[3pt]~~=~&\overrightarrow{\rm A’C’}\\[3pt]~~=~&\overrightarrow{\rm A’B’}+\overrightarrow{\rm B’C’}\\[3pt]~~=~&k\overrightarrow{\rm AB}+k\overrightarrow{\rm BC}\\[3pt]~~=~&k\overrightarrow{a}+k\overrightarrow{b}\end{split}\)
[終]
\({\small (2)}~-7\overrightarrow{a}+11\overrightarrow{b}\)
解法のPoint|ベクトルの式の計算方法
\({\small (2)}~\overrightarrow{x}=2\overrightarrow{a}-3\overrightarrow{b}\)
解法のPoint|等式を満たすベクトルの表し方
また、
\(~~~\overrightarrow{a}=-\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}~,~\overrightarrow{b}=-\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{c}\)
\(~~~\overrightarrow{\rm CB}=-\overrightarrow{a}-\overrightarrow{b}\)
\(~~~\overrightarrow{\rm DF}=-2\overrightarrow{a}-\overrightarrow{b}\)
解法のPoint|正六角形のベクトルの表し方
\(~~~\overrightarrow{b}=(2~,~-2)~,~|\overrightarrow{b}|=2\sqrt{2}\)
\(~~~\overrightarrow{c}=(-3~,~0)~,~|\overrightarrow{c}|=3\)
\(~~~\overrightarrow{d}=(0~,~-2)~,~|\overrightarrow{d}|=2\)
解法のPoint|ベクトルの成分と大きさ
\({\small (2)}~(9~,~-16)\)
\({\small (3)}~(0~,~1)\)
解法のPoint|ベクトルの成分を用いた計算
解法のPoint|ベクトルと平行な単位ベクトルの成分
\({\small (2)}~\overrightarrow{d}=-\overrightarrow{a}+\overrightarrow{b}\)
解法のPoint|成分によるベクトルの分解
\({\small (2)}~(0~,~-3)~,~3\)
\({\small (3)}~(-5~,~10)~,~5\sqrt{5}\)
解法のPoint|2点の座標とベクトルの成分・大きさ
\(~~~\left( -\displaystyle \frac{\,3\sqrt{2}\,}{\,2\,}~,~\displaystyle \frac{\,3\sqrt{2}\,}{\,2\,} \right)\)
解法のPoint|ベクトルと平行な単位ベクトルの成分
\({\small (3)}~-1\) \({\small (4)}~-3\)
解法のPoint|正方形における内積
\(~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{\theta}\)
ここで、\(\overrightarrow{a}\,//\,\overrightarrow{b}\) より、\(\theta=0^\circ~,~180^\circ\)
よって、
\(~~~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{0^\circ}=|\overrightarrow{a}||\overrightarrow{b}|\)
また、
\(~~~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{180^\circ}=-|\overrightarrow{a}||\overrightarrow{b}|\)
したがって、\(\overrightarrow{a}\,//\,\overrightarrow{b}\) ならば
\(\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\) または \(\overrightarrow{a}\cdot\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)
[終]
■ この問題の詳しい解説はこちら!
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) とすると、
\(k\overrightarrow{a}=(ka_1,ka_2)~,~k\overrightarrow{b}=(kb_1,kb_2)\)
よって、
\((k\overrightarrow{a})\cdot\overrightarrow{b}=ka_1b_1+ka_2b_2\)
また、
\(\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2\)
これより、
\(k(\overrightarrow{a}\cdot\overrightarrow{b})=k(a_1b_1+a_2b_2)\)
\(=ka_1b_1+ka_2b_2\)
また、
\(\overrightarrow{a}\cdot(k\overrightarrow{b})=a_1kb_1+a_2kb_2\)
\(=ka_1b_1+ka_2b_2\)
したがって、
\((k\overrightarrow{a})\cdot\overrightarrow{b}=k(\overrightarrow{a}\cdot\overrightarrow{b})=\overrightarrow{a}\cdot(k\overrightarrow{b})\)
[終]
[証明]
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)~,~\overrightarrow{c}=(c_1,c_2)\) とすると、
\(\overrightarrow{a}+\overrightarrow{b}=(a_1+b_1,a_2+b_2)\) より、
\(\begin{split}&(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}\\[3pt]~~=~&(a_1+b_1)c_1+(a_2+b_2)c_2\\[3pt]~~=~&a_1c_1+b_1c_1+a_2c_2+b_2c_2\\[3pt]~~=~&(a_1c_1+a_2c_2)+(b_1c_1+b_2c_2)\\[3pt]~~=~&\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{b}\cdot\overrightarrow{c}\end{split}\)
したがって、
\(~~~(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}=\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{b}\cdot\overrightarrow{c}\)
[終]
解法のPoint|内積の性質と大きさの2乗
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)~,~\overrightarrow{c}=(c_1,c_2)\) とすると、
\(\overrightarrow{b}-\overrightarrow{c}=(b_1-c_1,b_2-c_2)\) より、
\(\begin{split}&\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})\\[3pt]~~=~&a_1(b_1-c_1)+a_2(b_2-c_2)\\[3pt]~~=~&a_1b_1-a_1c_1+a_2b_2-a_2c_2\\[3pt]~~=~&(a_1b_1+a_2b_2)-(a_1c_1+a_2c_2)\\[3pt]~~=~&\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\end{split}\)
したがって、
\(~~~\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\)
[終]
解法のPoint|内積の性質と大きさの2乗
(左辺)
\(=|\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}+\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\(|\overrightarrow{a}+\overrightarrow{b}|^2=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\) [終]
\({\small (2)}~\)
(左辺)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{b}\cdot\overrightarrow{a}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\((\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
[終]
解法のPoint|ベクトルの等式の証明
問題
\({\small (2)}~\)\({\small (1)}\) より、
\(~~~\overrightarrow{\rm PQ}=\displaystyle \frac{\,m\,}{\,m+n\,}(\overrightarrow{c}-\overrightarrow{b})~~\cdots {\small [\,1\,]}\)
また、
\(\begin{eqnarray}~~~\overrightarrow{\rm BC}&=&\overrightarrow{\rm AC}-\overrightarrow{\rm AB}
\\[3pt]~~~&=&\overrightarrow{c}-\overrightarrow{b}~~\cdots {\small [\,2\,]}\end{eqnarray}\)
よって、\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm PQ}&=&\displaystyle \frac{\,m\,}{\,m+n\,}\overrightarrow{\rm BC}\end{eqnarray}\)
したがって、\(\overrightarrow{\rm PQ}\,//\,\overrightarrow{\rm BC}\) である [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( t=1 \) のとき、最小値 \( 6 \)
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\,|\,\overrightarrow{\rm OB}\,|\cos \theta~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
ここで、\(\triangle \rm OBD\) の余弦より、
\(\begin{eqnarray}~~~\cos \theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OD}\,|\,}{\,|\,\overrightarrow{\rm OB}\,|\,}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OB}\,|\cos \theta&=&|\,\overrightarrow{\rm OD}\,|
\end{eqnarray}\)
\(\small [\,1\,]\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\cdot|\,\overrightarrow{\rm OD}\,|~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
また、\(\triangle \rm OAC\) の余弦より、
\(\begin{eqnarray}~~~\cos \theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OC}\,|\,}{\,|\,\overrightarrow{\rm OA}\,|\,}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OA}\,|\cos \theta&=&|\,\overrightarrow{\rm OC}\,|
\end{eqnarray}\)
\(\small [\,1\,]\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OB}\,|\cdot|\,\overrightarrow{\rm OC}\,|~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
\(\overrightarrow{\rm OA}=\vec{a}\)、\(\overrightarrow{\rm OB}=\vec{b}\) より、\(\small [\,2\,]\) と \(\small [\,3\,]\) から、
\(\begin{eqnarray}~~~{\rm OA}\times{\rm OD}&=&\vec{a}\cdot\vec{b}\\[5pt]~~~{\rm OB}\times{\rm OC}&=&\vec{a}\cdot\vec{b}
\end{eqnarray}\)
したがって、
\(\begin{eqnarray}~~~{\rm OA}\times{\rm OD}&=&{\rm OB}\times{\rm OC}
\end{eqnarray}\) [終]
■ この問題の詳しい解説はこちら!
\({\small (4)}~\) \( -\displaystyle \frac{\,3\,}{\,2\,} \) \({\small (5)}~\) \( 2 \)
解法のPoint|正六角形における内積
■ この問題の詳しい解説はこちら!
2節 ベクトルの応用
\(m> n\) のとき、
\(~~~\overrightarrow{\rm AQ}=\displaystyle \frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}\)
\(m< n\) のとき、 \(~~~\overrightarrow{\rm AQ}=\displaystyle \frac{\,m\,}{\,n-m\,}\overrightarrow{\rm BA}=\displaystyle \frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}\) よって、どちらの場合でも、 \(\begin{eqnarray}~~~\overrightarrow{q}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm AQ}\\[3pt]~~~&=&\overrightarrow{\rm OA}+=\displaystyle \frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}\\[3pt]~~~&=&\overrightarrow{a}+=\displaystyle \frac{\,m\,}{\,m-n\,}(\overrightarrow{b}-\overrightarrow{a})\\[3pt]~~~&=&\displaystyle \frac{\,(m-n)\overrightarrow{a}+m\overrightarrow{b}-m\overrightarrow{a}\,}{\,m-n\,}\\[3pt]~~~&=&\displaystyle \frac{\,-n\overrightarrow{a}+m\overrightarrow{b}\,}{\,m-n\,}\end{eqnarray}\) [終]
解法のPoint|位置ベクトルの内分点・外分点・中点
\(~~~\displaystyle \frac{\,2\overrightarrow{a}+3\overrightarrow{b}\,}{\,5\,}\)
外分する点
\(~~~-2\overrightarrow{a}+3\overrightarrow{b}\)
\({\small (2)}~\)内分する点
\(~~~\displaystyle \frac{\,5\overrightarrow{a}+2\overrightarrow{b}\,}{\,7\,}\)
外分する点
\(~~~\displaystyle \frac{\,5\overrightarrow{a}-2\overrightarrow{b}\,}{\,3\,}\)
解法のPoint|位置ベクトルの内分点・外分点・中点
重心の位置ベクトルを \(\overrightarrow{g}\) とすると、
\(~~~\overrightarrow{g}=\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,3\,}\)
これより、
\(\begin{split}&\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}\\[3pt]~~=~&(\overrightarrow{a}-\overrightarrow{g})+(\overrightarrow{b}-\overrightarrow{g})+(\overrightarrow{c}-\overrightarrow{g})\\[3pt]~~=~&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{g}\\[3pt]~~=~&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})\\[3pt]~~=~&\overrightarrow{0}\end{split}\)
したがって、
\(~~~\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}\)
[終]
解法のPoint|重心の位置ベクトル
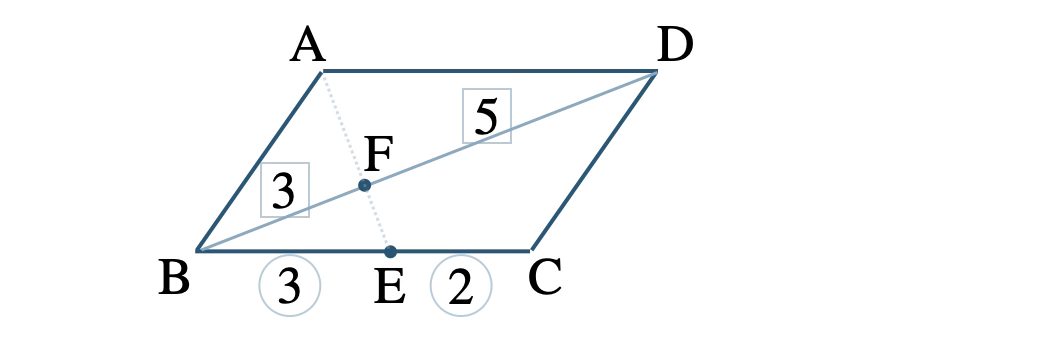

平行四辺形 \({\rm ABCD}\) で、\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とおくと、
\(\overrightarrow{\rm AC}=\overrightarrow{d}+\overrightarrow{b}\)
点 \( \rm E \) は辺 \( \rm BC \) を \(3:2\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AE}
&=&\displaystyle \frac{\,2{\, \small \times \,}\overrightarrow{\rm AB}+3{\, \small \times \,}\overrightarrow{\rm AC}\,}{\,3+2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{b}+3(\overrightarrow{d}+\overrightarrow{b})\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,5\,}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、点 \( \rm F \) は対角線 \( \rm BD \) を \(3:5\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF}
&=&\displaystyle \frac{\,5{\, \small \times \,}\overrightarrow{\rm AB}+3{\, \small \times \,}\overrightarrow{\rm AD}\,}{\,3+5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,8\,}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) を式変形して、\({\small [\,2\,]}\) と比較すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF}
&=&\displaystyle \frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,8\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,8\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,8\,}{\, \small \times \,}\displaystyle \frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,8\,}\,\overrightarrow{\rm AE} \hspace{20pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、点 \( \rm A~,~F~,~E \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)\(k:k-1\) に外分する
■ この問題の詳しい解説はこちら!
\({\small (2)}~\triangle {\rm PBC}:\triangle {\rm PCA}:\triangle {\rm PAB}=3:5:7\)
■ この問題の詳しい解説はこちら!
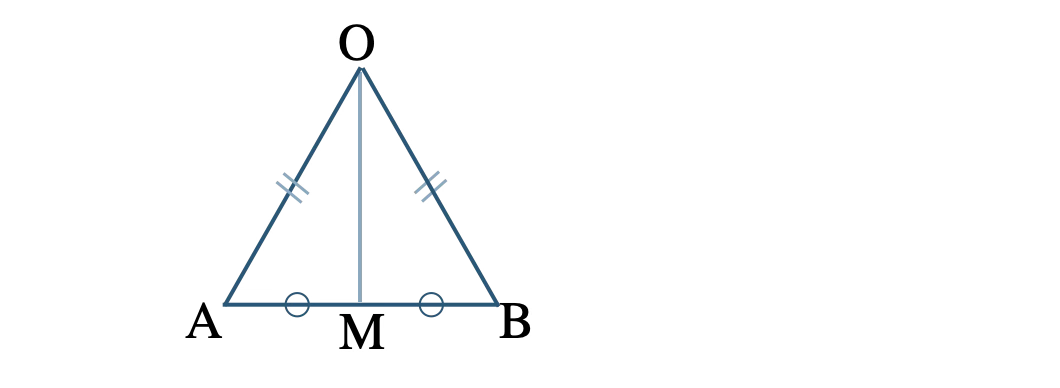
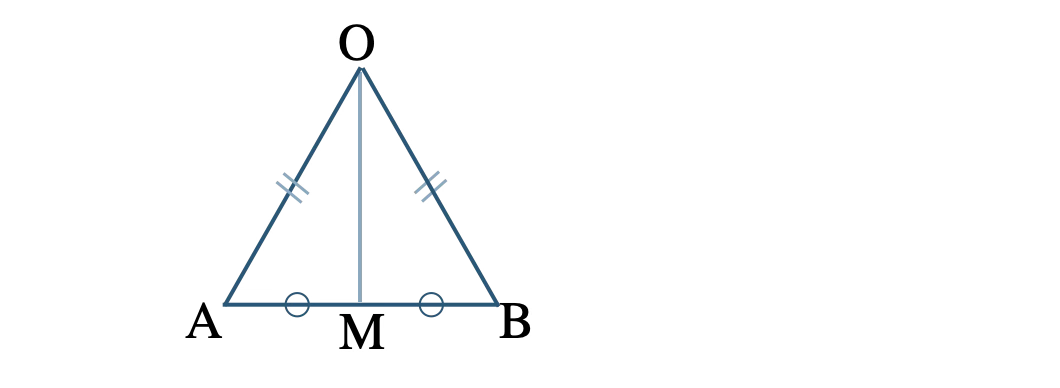
\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) とおくと、
\({\rm OA}={\rm OB}\) より、
\(|\overrightarrow{a}|=|\overrightarrow{b}|~ ~ ~ \cdots {\small [\,1\,]}\)
点 \({\rm M}\) は辺 \({\rm AB}\) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\,}{\,2\,}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}\,}{\,2\,}\end{eqnarray}\)
また、\(\overrightarrow{\rm AB}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&\overrightarrow{\rm OB}-\overrightarrow{\rm OA}\\[5pt]~~~&=&\overrightarrow{b}-\overrightarrow{a}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OM}\) と \(\overrightarrow{\rm AB}\) の内積は、
\({\small [\,1\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(|\overrightarrow{a}|^2-|\overrightarrow{a}|^2)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm OM}\neq\overrightarrow{0}~,~\overrightarrow{\rm AB}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm OM}\perp \overrightarrow{\rm AB}\)
したがって、\({\rm OM}\perp {\rm AB}\) [終]
■ この問題の詳しい解説はこちら!
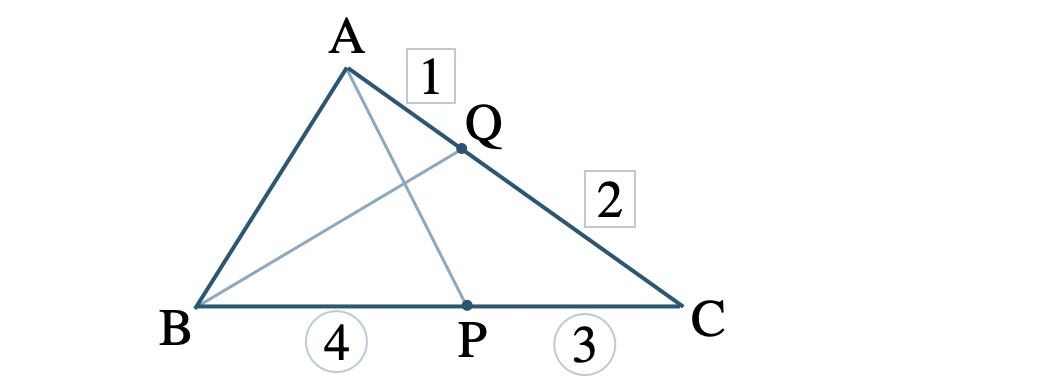

\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおくと、
\(\angle {\rm A}=90°\) より、
\(\overrightarrow{b}\cdot\overrightarrow{c}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\({\rm AB}:{\rm AC}=2:3\) より、
\(|\overrightarrow{c}|=\displaystyle \frac{\,3\,}{\,2\,}|\overrightarrow{b}|\)
よって、
\(|\overrightarrow{c}|^2=\displaystyle \frac{\,9\,}{\,4\,}|\overrightarrow{b}|^2~ ~ ~ \cdots {\small [\,2\,]}\)
点 \({\rm P}\) は線分 \({\rm BC}\) を \(4:3\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,3\cdot\overrightarrow{\rm AB}+4\cdot\overrightarrow{\rm AC}\,}{\,4+3\,}\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{b}+4\overrightarrow{c}\,}{\,7\,}\end{eqnarray}\)
点 \({\rm Q}\) は線分 \({\rm AC}\) を \(1:2\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
よって、\(\overrightarrow{\rm BQ}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BQ}&=&\overrightarrow{\rm AQ}-\overrightarrow{\rm AB}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}-\overrightarrow{b}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{\rm BQ}\) の内積は、
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) を代入すると、
\(\overrightarrow{\rm AP}\neq\overrightarrow{0}~,~\overrightarrow{\rm BQ}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AP}\perp \overrightarrow{\rm BQ}\)
したがって、\({\rm AP}\perp {\rm BQ}\) [終]
■ この問題の詳しい解説はこちら!
\( |\,\overrightarrow{a}\,|^2={a_1}^2+{a_2}^2~,~|\,\overrightarrow{b}\,|^2={b_1}^2+{b_2}^2 \)
\( \overrightarrow{a}\cdot\overrightarrow{b}=a_1\,b_1+a_2\,b_2 \)
\( S=\displaystyle\frac{\,1\,}{\,2\,}\sqrt{|\,\overrightarrow{a}\,|^2\,|\,\overrightarrow{b}\,|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2} \) に代入すると、
したがって、\( S=\displaystyle\frac{\,1\,}{\,2\,}|\,a_1\,b_2-a_2\,b_1\,| \) [終]
\({\small (2)}~3\)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\begin{eqnarray} \left\{\begin{array}{l}x=4-3t \\y=2t\end{array}\right.\end{eqnarray}\)
解法のPoint|方向ベクトルと直線の媒介変数表示
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
解法のPoint|法線ベクトルと2直線のなす角
\({\small (2)}~\)中心 \(\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}\)、半径 \(2\)
解法のPoint|中心と半径が条件の円のベクトル方程式
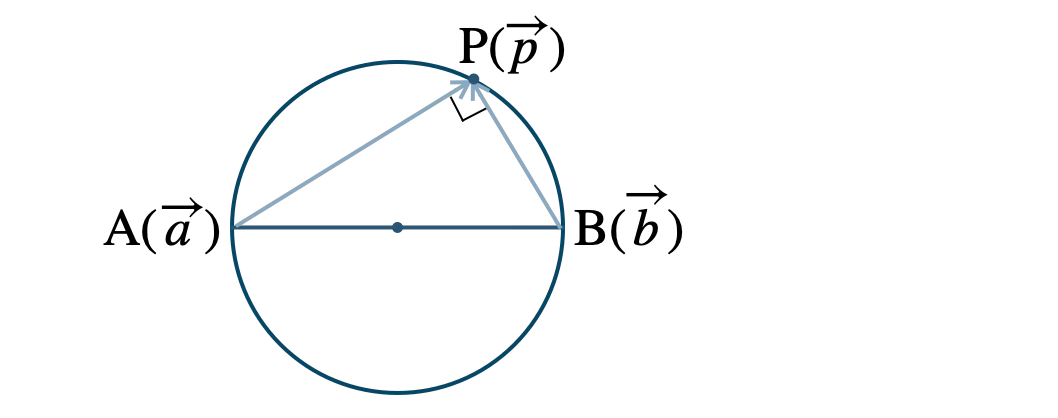

線分 \({\rm AB}\) を直径とする円より、\(\angle {\rm APB}=90^\circ\) となり、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{\rm BP}\) の内積は \(0\) となる
\(\overrightarrow{\rm AP}=\overrightarrow{p}-\overrightarrow{a}~,~\overrightarrow{\rm BP}=\overrightarrow{p}-\overrightarrow{b}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BP}&=&0
\\[3pt]~~~(\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{b})&=&0
\end{eqnarray}\)
[終]
解法のPoint|直径が条件の円のベクトル方程式


点 \({\rm A}\) と点 \({\rm P}\) が一致するとき、\(\overrightarrow{\rm AP}=\overrightarrow{0}\) より、
\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)
また、点 \({\rm A}\) と点 \({\rm P}\) が一致しないとき、\({\rm AP\perp CA}\) より、
\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)
よって、どちらの場合でも、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}&=&0
\\[3pt]~~~(\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})&=&0~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\(|\,\overrightarrow{\rm CA}\,|=r\) より、
\(\begin{eqnarray}~~~|\,\overrightarrow{a}-\overrightarrow{c}\,|&=&r
\\[3pt]~~~|\,\overrightarrow{a}-\overrightarrow{c}\,|^2&=&r^2
\\[3pt]~~~(\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})&=&r^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}+{\small [\,2\,]}\) より、両辺をそれぞれ加えると、
\(\begin{eqnarray}~~~&&(\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})
\\[3pt]&&\hspace{20pt}~~~+(\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\end{eqnarray}\)
\((\overrightarrow{a}-\overrightarrow{c})\) でくくると、
\(\begin{eqnarray}~~~(\overrightarrow{p}-\overrightarrow{a}+\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})&=&r^2
\\[3pt]~~~(\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})&=&r^2
\end{eqnarray}\)
したがって、この円の接線のベクトル方程式は、
\((\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\) [終]
■ この問題の詳しい解説はこちら!
問題
\({\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})~,~{\rm C}(\overrightarrow{c})\)
\({\rm P}(\overrightarrow{p})~,~{\rm Q}(\overrightarrow{q})~,~{\rm R}(\overrightarrow{r})\)
とおくと、
点 \({\rm P~,~ Q~,~R}\) が辺 \({\rm BC~,~ CA~,~ AB}\) をそれぞれ \(3:1\) に内分する点であることより、
\(\begin{eqnarray}~~~\overrightarrow{p}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{b}+3{\, \small \times \,}\overrightarrow{c}\,}{\,3+1\,}=\displaystyle \frac{\,\overrightarrow{b}+3\overrightarrow{c}\,}{\,4\,}
\\[5pt]~~~\overrightarrow{q}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{c}+3{\, \small \times \,}\overrightarrow{a}\,}{\,3+1\,}=\displaystyle \frac{\,\overrightarrow{c}+3\overrightarrow{a}\,}{\,4\,}
\\[5pt]~~~\overrightarrow{r}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{a}+3{\, \small \times \,}\overrightarrow{b}\,}{\,3+1\,}=\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}\,}{\,4\,}
\end{eqnarray}\)
ここで、\(\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}\) を \(\overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c}\) を用いて表すと、
\(\begin{eqnarray}~~~&&\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+3\overrightarrow{c}+\overrightarrow{c}+3\overrightarrow{a}+\overrightarrow{a}+3\overrightarrow{b}\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\overrightarrow{a}+4\overrightarrow{b}+4\overrightarrow{c}\,}{\,4\,}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}
\end{eqnarray}\)
これより、等式の左辺は、
\(\begin{eqnarray}~~~&&\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}
\\[5pt]~~~&=&(\overrightarrow{p}-\overrightarrow{a})+(\overrightarrow{q}-\overrightarrow{b})+(\overrightarrow{r}-\overrightarrow{c})
\\[5pt]~~~&=&(\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r})-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\overrightarrow{0}
\end{eqnarray}\)
したがって、\(\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}=\overrightarrow{0}\) [終]
■ この問題の詳しい解説はこちら!
\( {\rm LP}:{\rm PM}=5:3~,~{\rm OP}:{\rm PN}=1:1 \)
■ この問題の詳しい解説はこちら!
\\[5pt]~l\overrightarrow{\rm AP}+m(\overrightarrow{\rm AP}-\overrightarrow{\rm AB})+n(\overrightarrow{\rm AP}-\overrightarrow{\rm AC})&=&\overrightarrow{0}
\\[5pt]~l\overrightarrow{\rm AP}+m\overrightarrow{\rm AP}-m\overrightarrow{\rm AB}+n\overrightarrow{\rm AP}-n\overrightarrow{\rm AC}&=&\overrightarrow{0}
\end{eqnarray}\)
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおくと、
\(\begin{eqnarray}~~~(l+m+n)\overrightarrow{\rm AP}-m\overrightarrow{b}-n\overrightarrow{c}&=&\overrightarrow{0}
\\[5pt]~(l+m+n)\overrightarrow{\rm AP}&=&m\overrightarrow{b}+n\overrightarrow{c}
\\[5pt]~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,m\overrightarrow{b}+n\overrightarrow{c}\,}{\,l+m+n\,}
\end{eqnarray}\)
分子の係数の和 \(m+n\) を分母分子にかけて、実数倍×内分のベクトルの形に式変形すると、
\(\begin{eqnarray}~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,m+n\,}{\,m+n\,}{\, \small \times \,}\frac{\,m\overrightarrow{b}+n\overrightarrow{c}\,}{\,l+m+n\,}
\\[5pt]~~~&=&\displaystyle \frac{\,m+n\,}{\,l+m+n\,}{\, \small \times \,}\frac{\,m\overrightarrow{b}+n\overrightarrow{c}\,}{\,m+n\,}
\end{eqnarray}\)
ここで、辺 \({\rm BC}\) を \(n:m\) に内分する点を \({\rm Q}\) とすると、\(\overrightarrow{\rm AQ}=\displaystyle \frac{\,m\overrightarrow{b}+n\overrightarrow{c}\,}{\,m+n\,}\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,m+n\,}{\,l+m+n\,}\,\overrightarrow{\rm AQ}
\end{eqnarray}\)
\(l~,~m~,~n\) がすべて正のとき、
\(n\gt 0~,~m\gt 0\) より、点 \({\rm Q}\) は辺 \({\rm BC}\) 上にある(\({\rm B}\) と \({\rm C}\) の間)
また、\(l\gt 0~,~m+n\gt 0\) より、
\(0\lt \displaystyle \frac{\,m+n\,}{\,l+m+n\,}\lt 1\)
点 \({\rm P}\) は線分 \({\rm AQ}\) 上にある(\({\rm A}\) と \({\rm Q}\) の間)
したがって、
点 \({\rm P}\) は \(\triangle {\rm ABC}\) の内部にある
\({\small (2)}~\)
\(\begin{eqnarray}~~~\triangle {\rm PBC}&=&\displaystyle \frac{\,l\,}{\,l+m+n\,}
\\[5pt]~~~\triangle {\rm PCA}&=&\displaystyle \frac{\,m\,}{\,l+m+n\,}
\\[5pt]~~~\triangle {\rm PAB}&=&\displaystyle \frac{\,n\,}{\,l+m+n\,}
\end{eqnarray}\)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)\(\overrightarrow{\rm OB^{\prime}}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OB}\) を満たす点 \({\rm B^{\prime}}\) をおくとき、点 \(\rm P\) の存在範囲は \(\triangle {\rm OAB^{\prime}}\) の周および内部
■ この問題の詳しい解説はこちら!
\(\overrightarrow{m}=(a_1~,~b_1)\)
直線 \(a_2x+b_2y+c_2=0\) の法線ベクトルは、
\(\overrightarrow{n}=(a_2~,~b_2)\)
2直線が平行のとき、それぞれの法線ベクトル \(\overrightarrow{m},\,\overrightarrow{n}\) のなす角は \(0^\circ\) または \(180^\circ\) となるので、
\(\overrightarrow{m}\cdot\overrightarrow{n}=|\,\overrightarrow{m}\,|\,|\,\overrightarrow{n}\,|\cos 0^\circ=|\,\overrightarrow{m}\,|\,|\,\overrightarrow{n}\,|\)
または、
\(\overrightarrow{m}\cdot\overrightarrow{n}=|\,\overrightarrow{m}\,|\,|\,\overrightarrow{n}\,|\cos 180^\circ=-|\,\overrightarrow{m}\,|\,|\,\overrightarrow{n}\,|\)
どちらでも両辺を2乗すると、
\(~~~(\overrightarrow{m}\cdot\overrightarrow{n})^2=|\,\overrightarrow{m}\,|^2\,|\,\overrightarrow{n}\,|^2~ ~ ~ \cdots {\small [\,1\,]}\)
ここで、内積を成分で計算すると、\(\overrightarrow{m}\cdot\overrightarrow{n}=a_1\,a_2+b_1\,b_2\) であるので、
\(\begin{eqnarray}~~~&&(\overrightarrow{m}\cdot\overrightarrow{n})^2
\\[3pt]~~~&=&(a_1\,a_2+b_1\,b_2)^2
\\[3pt]~~~&=&{a_1}^2\,{a_2}^2+2a_1a_2b_1b_2+{b_1}^2\,{b_2}^2
\end{eqnarray}\)
また、\(|\,\overrightarrow{m}\,|^2={a_1}^2+{b_1}^2~,~|\,\overrightarrow{n}\,|^2={a_2}^2+{b_2}^2\) より、
\(\begin{eqnarray}~~~&&|\,\overrightarrow{m}\,|^2\,|\,\overrightarrow{n}\,|^2
\\[3pt]~~~&=&({a_1}^2+{b_1}^2)({a_2}^2+{b_2}^2)
\\[3pt]~~~&=&{a_1}^2{a_2}^2+{a_1}^2{b_2}^2+{b_1}^2{a_2}^2+{b_1}^2{b_2}^2
\end{eqnarray}\)
\(\small [\,1\,]\) に代入して整理すると、
\(\begin{eqnarray}~~~{a_1}^2{b_2}^2-2a_1a_2b_1b_2+{b_1}^2{a_2}^2&=&0
\\[3pt]~~~({a_1}{b_2}-{a_2}{b_1})^2&=&0
\\[3pt]~~~{a_1}{b_2}-{a_2}{b_1}&=&0
\end{eqnarray}\)
また、2直線が垂直のとき、それぞれの法線ベクトル \(\overrightarrow{m}~,~\overrightarrow{n}\) も垂直となり、内積が \(0\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{m}\cdot\overrightarrow{n}&=&0
\\[3pt]~~~a_1a_2+b_1b_2&=&0
\end{eqnarray}\)
したがって、
2直線が平行のとき、\({a_1}{b_2}-{a_2}{b_1}=0\)
2直線が垂直のとき、\(a_1a_2+b_1b_2=0\) [終]
解法のPoint|2直線の平行・垂直と法線ベクトル
\({\small (2)}~\)点 \({\rm O}\) が中心で、半径 \(|\,\overrightarrow{a}\,|\) の円
■ この問題の詳しい解説はこちら!
3節 空間におけるベクトル
\(~~~{\rm A}(2~,~0~,~0)\)
\(~~~{\rm B}(0~,~5~,~0)\)
\(~~~{\rm C}(0~,~0~,~4)\)
解法のPoint|平面に下ろした交点の座標
\({\small (2)}~(3~,~-2~,~1)\)
\({\small (3)}~(3~,~-2~,~-1)\)
\({\small (4)}~(-3~,~2~,~-1)\)
\({\small (5)}~(-3~,~-2~,~-1)\)
解法のPoint|平面・軸・原点に対称な点の座標
\(y=3\) は \(zx\) 平面に平行で \(y\) 軸との交点の \(3\) の平面
\(z=-1\) は \(xy\) 平面に平行で \(z\) 軸との交点の \(-2\) の平面
解法のPoint|座標空間の点を通る平面の方程式
\({\small (3)}~P^{\prime}(2~,~-1~,~4)\)
解法のPoint|座標空間の点を通る平面の方程式
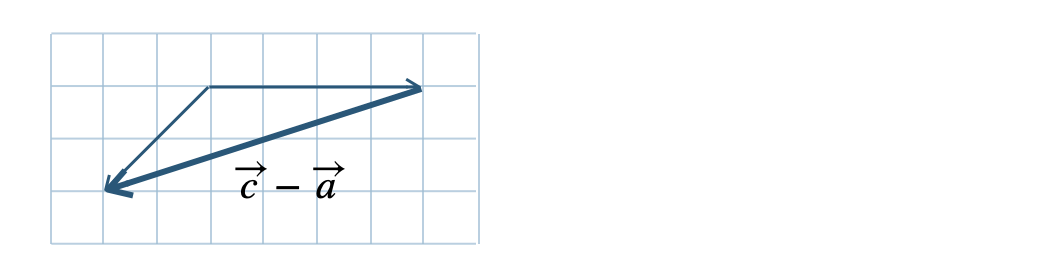
\({\small (2)}~\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}\)
\({\small (3)}~2\overrightarrow{b}\)
\({\small (4)}~2\overrightarrow{b}-2\overrightarrow{a}\)
解法のPoint|平行六面体とベクトルの加法・減法
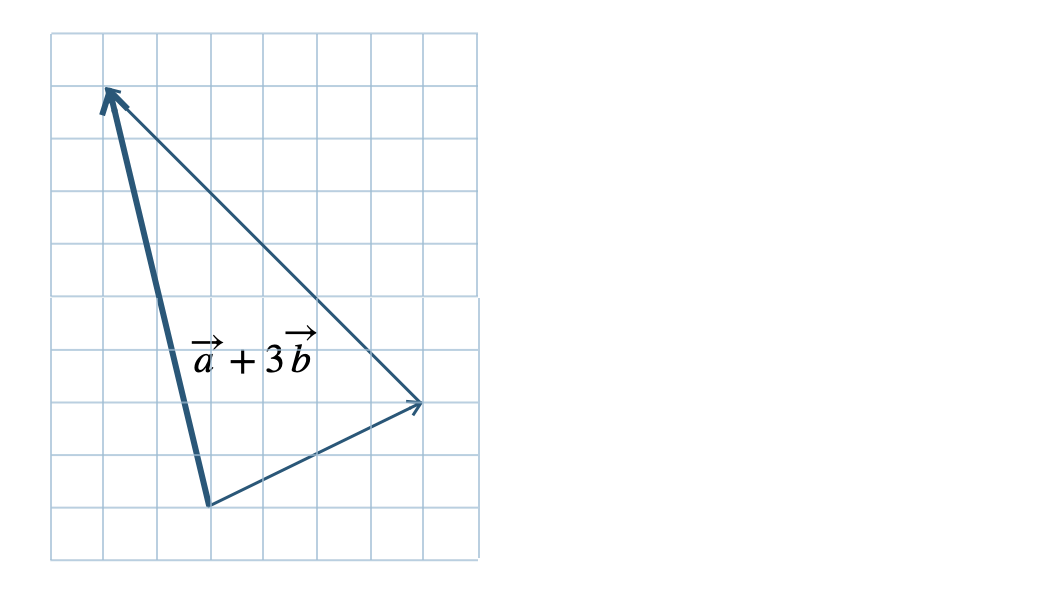
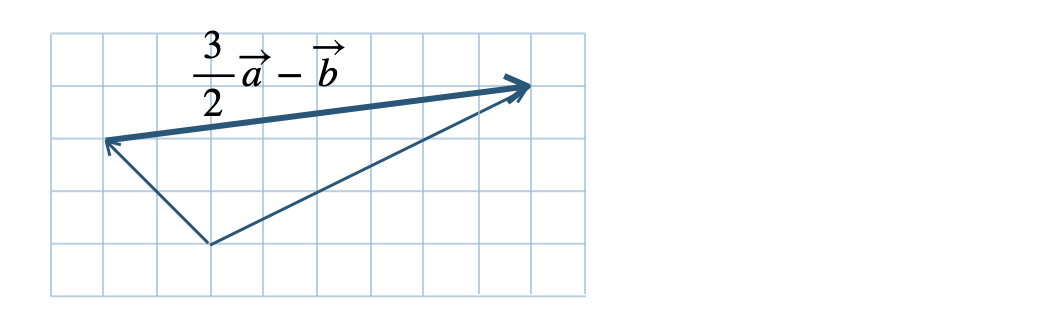
\({\small (2)}~2\overrightarrow{a}+3\overrightarrow{b}+\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{c}\)
\({\small (3)}~2\overrightarrow{a}-3\overrightarrow{b}\)
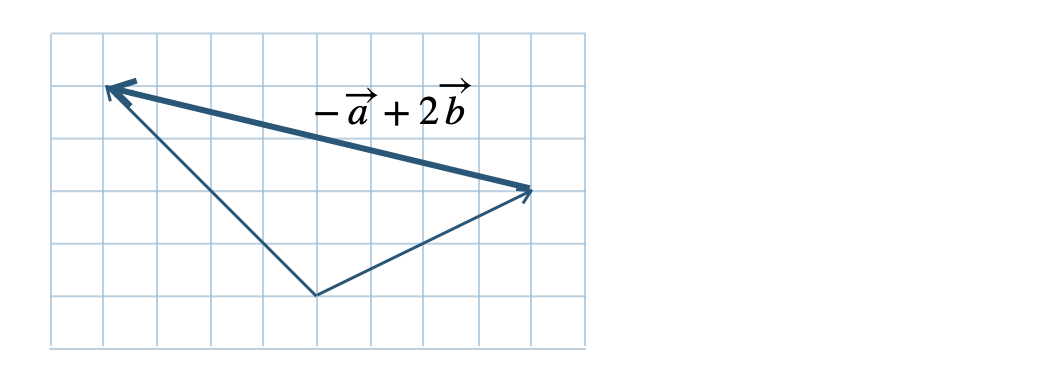
\({\small (4)}~-2\overrightarrow{a}+3\overrightarrow{b}+\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{c}\)
解法のPoint|平行六面体とベクトルの実数倍
解法のPoint|成分計算とベクトルの表し方
\(|\overrightarrow{e_1}|=|\overrightarrow{e_2}|=|\overrightarrow{e_3}|=1\) より、
\(~~~\overrightarrow{e_1}\cdot\overrightarrow{e_1}=1\times1\times\cos{0^\circ}=1\)
同様に、
\(~~~\overrightarrow{e_2}\cdot\overrightarrow{e_2}=1~,~\overrightarrow{e_3}\cdot\overrightarrow{e_3}=1\)
したがって、
\(~~~\overrightarrow{e_1}\cdot\overrightarrow{e_1}=\overrightarrow{e_2}\cdot\overrightarrow{e_2}=\overrightarrow{e_3}\cdot\overrightarrow{e_3}=1\)
[終]
\({\small (2)}~\)[証明]
\(|\overrightarrow{e_1}|=|\overrightarrow{e_2}|=|\overrightarrow{e_3}|=1\) より、
\(~~~\overrightarrow{e_1}\cdot\overrightarrow{e_2}=1\times1\times\cos{90^\circ}=0\)
同様に、
\(~~~\overrightarrow{e_2}\cdot\overrightarrow{e_3}=0~,~\overrightarrow{e_3}\cdot\overrightarrow{e_1}=0\)
したがって、
\(~~~\overrightarrow{e_1}\cdot\overrightarrow{e_2}=\overrightarrow{e_2}\cdot\overrightarrow{e_3}=\overrightarrow{e_3}\cdot\overrightarrow{e_1}=0\)
[終]
\({\small (3)}~0\) \({\small (4)}~-4\)
解法のPoint|空間ベクトルの内積計算
外分する点
解法のPoint|空間の位置ベクトルと内分点・外分点・中点
\(~~~\overrightarrow{m}=\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}\,}{\,2\,}\)
重心 \({\rm G}\) は線分 \({\rm AM}\) を \(2:1\) に内分する点であるので、
\(\begin{eqnarray}~~~\overrightarrow{g}&=&\displaystyle \frac{\,\overrightarrow{a}+2\overrightarrow{m}\,}{\,2+1\,}\\[3pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,3\,}\end{eqnarray}\)
[終]
解法のPoint|空間内の三角形の重心の位置ベクトル
\( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \)
とおくと、
点 \( {\rm P} (\, \overrightarrow{p} \,) \) は \( {\rm OA} \) の中点より、
\( \overrightarrow{p}=\displaystyle \frac{\,\overrightarrow{a}\,}{\,2\,} \)
点 \( {\rm R} (\, \overrightarrow{r} \,) \) は \( {\rm BC} \) の中点より、
\( \overrightarrow{r}=\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,} \)
点 \( {\rm E} (\, \overrightarrow{e} \,) \) は \( {\rm AB} \) を \( 1:2 \) に内分する点より、
\( \overrightarrow{e}=\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}\,}{\,3\,} \)
点 \( {\rm F} (\, \overrightarrow{f} \,) \) は \( {\rm OC} \) を \( 1:2 \) に内分する点より、
\( \overrightarrow{f}=\displaystyle \frac{\,\overrightarrow{c}\,}{\,3\,} \)
ここで、線分 \( {\rm PR} \) を \( 1:2 \) に内分する点は、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\overrightarrow{p}+\overrightarrow{r}\,}{\,3\,}&=&\displaystyle \frac{\,2\cdot\displaystyle \frac{\,\overrightarrow{a}\,}{\,2\,}+\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,6\,}\end{eqnarray}\)
また、線分 \( {\rm EF} \) の中点は、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{e}+\overrightarrow{f}\,}{\,2\,}&=&\displaystyle \frac{\,\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}\,}{\,3\,}+\displaystyle \frac{\,\overrightarrow{c}\,}{\,3\,}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,3\,}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,6\,}\end{eqnarray}\)
したがって、線分 \( {\rm PR} \) を \( 1:2 \) に内分する点と線分 \( {\rm EF} \) の中点は一致する [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)[証明] \( \triangle {\rm ABC} \) の重心が \( {\rm G’} \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG’}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,9\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\(\small (1)\) と \(\small [\,4\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG’}&=&\displaystyle \frac{\,3\,}{\,9\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\cdot\displaystyle \frac{\,2\,}{\,9\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm OG}
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm OG’}=\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm OG} \) より、
直線 \( {\rm OG} \) は \( \triangle {\rm ABC} \) の重心 \( {\rm G’} \) を通る [終]
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
解法のPoint|中心と半径が条件の球面の方程式
\({\small (2)}~(x+1)^2+y^2+(z-3)^2=36\)
解法のPoint|直径の両端が条件の球面の方程式
問題
解法のPoint|座標空間の点を通る平面の方程式
\({\small (2)}~\) \( {\rm B}(1~,~6~,~-14) \)
解法のPoint|空間の点に関して対称な点
\({\small (3)}~\) \( x=5 \)
解法のPoint|座標空間の点を通る平面の方程式
解法のPoint|成分計算とベクトルの表し方
解法のPoint|空間の三角形の内角の大きさ
\(\overrightarrow{\rm AP}=s\overrightarrow{\rm AB}+t\overrightarrow{\rm AC}\)
と表せる。
条件より、
\(\overrightarrow{\rm AB}\perp\overrightarrow{n}\) なので \(\overrightarrow{\rm AB}\cdot\overrightarrow{n}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\(\overrightarrow{\rm AC}\perp\overrightarrow{n}\) なので \(\overrightarrow{\rm AC}\cdot\overrightarrow{n}=0~ ~ ~ \cdots {\small [\,2\,]}\)
ここで、\( \overrightarrow{\rm AP} \) と \( \overrightarrow{n} \) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{n}&=&(s\overrightarrow{\rm AB}+t\overrightarrow{\rm AC})\cdot\overrightarrow{n}\\[5pt]~~~&=&s\overrightarrow{\rm AB}\cdot\overrightarrow{n}+t\overrightarrow{\rm AC}\cdot\overrightarrow{n}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、
\(\begin{eqnarray}\hspace{35pt}&=&s\cdot 0+t\cdot 0\\[5pt]~~~&=&0\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AP}\neq 0~,~\overrightarrow{n}\neq 0~,~\overrightarrow{\rm AP}\cdot\overrightarrow{n}=0 \) より、\( \overrightarrow{\rm AP}\perp\overrightarrow{n} \) [終]
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)\({\small (1)}\) より、\( \overrightarrow{\rm OP}=\left(\,\begin{array}{c}4\\[2pt]3\\[2pt]2\end{array}\,\right) \) であるので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}&=&4\cdot3+3\cdot(-6)+2\cdot3
\\[3pt]~~~&=&12-18+6
\\[3pt]~~~&=&0\end{eqnarray}\)
よって、\( \overrightarrow{\rm OP}\cdot\overrightarrow{\rm AB}=0 \) より、\(\rm AB\perp OP\) である
■ この問題の詳しい解説はこちら!
練習問題
\(\begin{split}&(\,|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|\,)^2
\\[3pt]~~=~&|\,\overrightarrow{a}\,|^{2}+2|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|+|\,\overrightarrow{b}\,|^{2}
\end{split}\)
左辺の式の2乗は、
\(\begin{split}&|\,\overrightarrow{a}+\overrightarrow{b}\,|^{2}
\\[3pt]~~=~&(\,\overrightarrow{a}+\overrightarrow{b}\,)\cdot(\,\overrightarrow{a}+\overrightarrow{b}\,)
\\[3pt]~~=~&\overrightarrow{a}\cdot\overrightarrow{a}+\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}
\\[3pt]~~=~&|\,\overrightarrow{a}\,|^{2}+2\,\overrightarrow{a}\cdot\overrightarrow{b}+|\,\overrightarrow{b}\,|^{2}
\end{split}\)
よって、右辺の式の2乗ー左辺の式の2乗は、
\(\begin{split}&(\,|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|\,)^2
-|\,\overrightarrow{a}+\overrightarrow{b}\,|^{2}
\\[3pt]~~=~&(|\,\overrightarrow{a}\,|^{2}+2|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|+|\,\overrightarrow{b}\,|^{2})
\\[3pt]~~~&~~~~~~~~~~-(|\,\overrightarrow{a}\,|^{2}+2\,\overrightarrow{a}\cdot\overrightarrow{b}+|\,\overrightarrow{b}\,|^{2})
\\[3pt]~~=~&|\,\overrightarrow{a}\,|^{2}+2|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|+|\,\overrightarrow{b}\,|^{2}
\\[3pt]~~~&~~~~~~~~~~-|\,\overrightarrow{a}\,|^{2}-2\,\overrightarrow{a}\cdot\overrightarrow{b}-|\,\overrightarrow{b}\,|^{2}
\\[3pt]~~=~&2|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|-2\,\overrightarrow{a}\cdot\overrightarrow{b}
\\[3pt]~~=~&2(\,|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|-\overrightarrow{a}\cdot\overrightarrow{b}\,)
\end{split}\)
ここで、\(-1{\small ~≦~}\cos\theta {\small ~≦~}1\) の各辺に \(|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\) をかけると、
\(-|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|{\small ~≦~}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\cos\theta {\small ~≦~}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\)
\(\overrightarrow{a}\cdot\overrightarrow{b}=|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\cos\theta\) より、
\(-|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|{\small ~≦~}\overrightarrow{a}\cdot\overrightarrow{b}{\small ~≦~}|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|\)
よって、\(|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|-\overrightarrow{a}\cdot\overrightarrow{b}{\small ~≧~}0\) となり、
\(2(|\,\overrightarrow{a}\,|\,|\,\overrightarrow{b}\,|-\overrightarrow{a}\cdot\overrightarrow{b}){\small ~≧~}0\)
これより、
\(\begin{eqnarray}~~~(\,|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|\,)^2
-|\,\overrightarrow{a}+\overrightarrow{b}\,|^{2}{\small ~≧~} 0
\end{eqnarray}\)
したがって、
\(|\,\overrightarrow{a}+\overrightarrow{b}\,|^{2}{\small ~≦~}(\,|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|\,)^2\)
ここで、
\(|\,\overrightarrow{a}+\overrightarrow{b}\,|{\small ~≧~}0~,~|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|{\small ~≧~}0\) より、
\(|\,\overrightarrow{a}+\overrightarrow{b}\,|{\small ~≦~}|\,\overrightarrow{a}\,|+|\,\overrightarrow{b}\,|\) [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~\) \( t_1=2 \) のとき、最小値 \( 3 \)
\({\small (3)}~\)\((\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}\) を計算すると、
\(\begin{eqnarray}~~~(\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}&=&\overrightarrow{a}\cdot\overrightarrow{b}+t_1\overrightarrow{b}\cdot\overrightarrow{b}
\\[3pt]~~~&=&\overrightarrow{a}\cdot\overrightarrow{b}+t_1|\,\overrightarrow{b}\,|^2\end{eqnarray}\)
\( \overrightarrow{a}\cdot\overrightarrow{b}=-8~,~t_1=2~,~|\,\overrightarrow{b}\,|=2 \) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&-8+2\cdot 2^2
\\[3pt]~~~&=&-8+8
\\[3pt]~~~&=&0\end{eqnarray}\)
よって、\((\overrightarrow{a}+t_1\overrightarrow{b})\cdot\overrightarrow{b}=0\) より、\(\overrightarrow{a}+t_1\overrightarrow{b}\) と \(\overrightarrow{b}\) は垂直である
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=| \overrightarrow{b} |^2+| \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \overrightarrow{\rm AM} \) は中点の公式より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AM}&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,}
\end{eqnarray}\)
これより、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{b}+\overrightarrow{c} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{b}+\overrightarrow{c})\cdot(\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\end{eqnarray}\)
次に、\( \overrightarrow{\rm BM}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~| \overrightarrow{\rm BM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{c}-\overrightarrow{b}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{c}-\overrightarrow{b} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{c}-\overrightarrow{b})\cdot(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\end{eqnarray}\)
以上より、右辺は、
\\[5pt]~~~&=&2 \cdot \displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2+ | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\,( 2\,| \overrightarrow{b} |^2 + 2\,| \overrightarrow{c} |^2 )
\\[5pt]~~~&=&| \overrightarrow{b} |^2 + | \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
よって、\(\small [\,1\,]\) と \(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=2( | \overrightarrow{\rm AM} |^2+| \overrightarrow{\rm BM} |^2 )
\end{eqnarray}\)
したがって、\({\rm AB^2+AC^2=2(AM^2+BM^2)}\) [終]
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) より、
\end{eqnarray}\)
また、\( \overrightarrow{\rm AP} \) は内分点の公式より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,n\,\overrightarrow{b}+m\,\overrightarrow{c}\,}{\,m+n\,}
\end{eqnarray}\)
これより、
&=&\left| \displaystyle \frac{\,n\,\overrightarrow{b}+m\,\overrightarrow{c}\,}{\,m+n\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,(m+n)^2\,}\,| n\,\overrightarrow{b}+m\,\overrightarrow{c} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,(m+n)^2\,}\,(n\,\overrightarrow{b}+m\,\overrightarrow{c})\cdot(n\,\overrightarrow{b}+m\,\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,(m+n)^2\,}\,( n^2\,| \overrightarrow{b} |^2 + 2mn\,\overrightarrow{b}\cdot\overrightarrow{c} + m^2\,| \overrightarrow{c} |^2 )
\end{eqnarray}\)
次に、\( \overrightarrow{\rm BP}=\displaystyle \frac{\,m\,}{\,m+n\,}\overrightarrow{\rm BC} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BP}&=&\displaystyle \frac{\,m\,}{\,m+n\,}(\overrightarrow{c}-\overrightarrow{b})
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~| \overrightarrow{\rm BP} |^2
&=&\left| \displaystyle \frac{\,m\,(\overrightarrow{c}-\overrightarrow{b})\,}{\,m+n\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,m^2\,}{\,(m+n)^2\,}\,| \overrightarrow{c}-\overrightarrow{b} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,m^2\,}{\,(m+n)^2\,}\,(\overrightarrow{c}-\overrightarrow{b})\cdot(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,m^2\,}{\,(m+n)^2\,}\,( | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\end{eqnarray}\)
次に、\( \overrightarrow{\rm CP}=\displaystyle \frac{\,n\,}{\,m+n\,}\overrightarrow{\rm CB} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm CP}&=&\displaystyle \frac{\,n\,}{\,m+n\,}(\overrightarrow{b}-\overrightarrow{c})
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~| \overrightarrow{\rm CP} |^2
&=&\left| \displaystyle \frac{\,n\,(\overrightarrow{b}-\overrightarrow{c})\,}{\,m+n\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,n^2\,}{\,(m+n)^2\,}\,| \overrightarrow{b}-\overrightarrow{c} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,n^2\,}{\,(m+n)^2\,}\,(\overrightarrow{b}-\overrightarrow{c})\cdot(\overrightarrow{b}-\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,n^2\,}{\,(m+n)^2\,}\,( | \overrightarrow{b} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\end{eqnarray}\)
以上より、右辺は、
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,m+n\,}\,( n^2\,| \overrightarrow{b} |^2 + 2mn\,\overrightarrow{b}\cdot\overrightarrow{c} + m^2\,| \overrightarrow{c} |^2 )+ \frac{\,nm^2\,}{\,(m+n)^2\,}\,( | \overrightarrow{b} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )+ \frac{\,mn^2\,}{\,(m+n)^2\,}\,( | \overrightarrow{b} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,m+n\,}\,( n^2\,| \overrightarrow{b} |^2 + 2mn\,\overrightarrow{b}\cdot\overrightarrow{c} + m^2\,| \overrightarrow{c} |^2 )+ \frac{\,mn\,}{\,m+n\,}\,( | \overrightarrow{b} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,m+n\,}\,( n^2\,| \overrightarrow{b} |^2 + 2mn\,\overrightarrow{b}\cdot\overrightarrow{c} + m^2\,| \overrightarrow{c} |^2+ mn\,| \overrightarrow{b} |^2 – 2mn\,\overrightarrow{b}\cdot\overrightarrow{c} + mn\,| \overrightarrow{c} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,m+n\,}\,\left\{(n^2+mn)\,| \overrightarrow{b} |^2 + (m^2+mn)\,| \overrightarrow{c} |^2\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,m+n\,}\,\left\{n(m+n)\,| \overrightarrow{b} |^2 + m(m+n)\,| \overrightarrow{c} |^2\right\}
\\[5pt]~~~&=&n\,| \overrightarrow{b} |^2 + m\,| \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
よって、\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、
\(\begin{eqnarray}~~~&&n\,| \overrightarrow{\rm AB} |^2+m\,| \overrightarrow{\rm AC} |^2
\\[3pt]~~~&=&(m+n)| \overrightarrow{\rm AP} |^2+n\,| \overrightarrow{\rm BP} |^2+m\,| \overrightarrow{\rm CP} |^2
\end{eqnarray}\)
したがって、
\(\begin{eqnarray}~~~&&n\,{\rm AB^2}+m\,{\rm AC^2}\\[3pt]~~~&=&(m+n){\rm AP^2}+n\,{\rm BP^2}+m\,{\rm CP^2}\end{eqnarray}\)
[終]
■ この問題の詳しい解説はこちら!
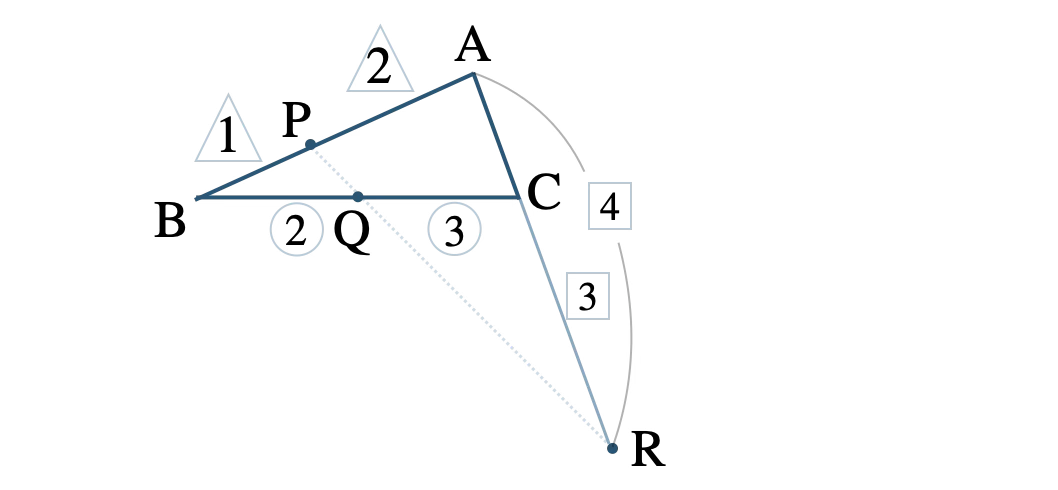

\(\triangle {\rm ABC}\) で、\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおく。
点 \( \rm P \) は辺 \( \rm AB \) を \(2:1\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}
&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}
\end{eqnarray}\)
点 \( \rm Q \) は辺 \( \rm BC \) を \(2:3\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}
&=&\displaystyle \frac{\,3{\, \small \times \,}\overrightarrow{\rm AB}+2{\, \small \times \,}\overrightarrow{\rm AC}\,}{\,2+3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{b}+2\overrightarrow{c}\,}{\,5\,}
\end{eqnarray}\)
点 \( \rm R \) は辺 \( \rm CA \) を \(3:4\) に外分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AR}
&=&\displaystyle \frac{\,-4{\, \small \times \,}\overrightarrow{\rm AC}+3{\, \small \times \,}\overrightarrow{\rm AA}\,}{\,3-4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-4\overrightarrow{c}\,}{\,-1\,}
\\[5pt]~~~&=&4\overrightarrow{c}
\end{eqnarray}\)
よって、\(\overrightarrow{\rm PQ}\) を求めると、
\(\begin{eqnarray}~~~\overrightarrow{\rm PQ}
&=&\overrightarrow{\rm AQ}-\overrightarrow{\rm AP}
\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{b}+2\overrightarrow{c}\,}{\,5\,}-\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,9\overrightarrow{b}+6\overrightarrow{c}-10\overrightarrow{b}\,}{\,15\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-\overrightarrow{b}+6\overrightarrow{c}\,}{\,15\,}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\(\overrightarrow{\rm PR}\) を求めると、
\(\begin{eqnarray}~~~\overrightarrow{\rm PR}
&=&\overrightarrow{\rm AR}-\overrightarrow{\rm AP}
\\[5pt]~~~&=&4\overrightarrow{c}-\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}
\\[5pt]~~~&=&-\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}+4\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,-2\overrightarrow{b}+12\overrightarrow{c}\,}{\,3\,}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) を式変形して、\({\small [\,2\,]}\) と比較すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm PR}
&=&\displaystyle \frac{\,-2\overrightarrow{b}+12\overrightarrow{c}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2(-\overrightarrow{b}+6\overrightarrow{c})\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}{\, \small \times \,}15{\, \small \times \,}\displaystyle \frac{\,-\overrightarrow{b}+6\overrightarrow{c}\,}{\,15\,}
\\[5pt]~~~&=&10\,\overrightarrow{\rm PQ} \hspace{20pt}(\,∵~ {\small [\,1\,]}\,)
\end{eqnarray}\)
したがって、点 \( \rm P~,~Q~,~R \) は一直線上にある [終]
■ この問題の詳しい解説はこちら!
\( y \) 軸とのなす角は \( 90^{\circ} \)
\( z \) 軸とのなす角は \( 60^{\circ} \)
■ この問題の詳しい解説はこちら!
■ この問題の詳しい解説はこちら!
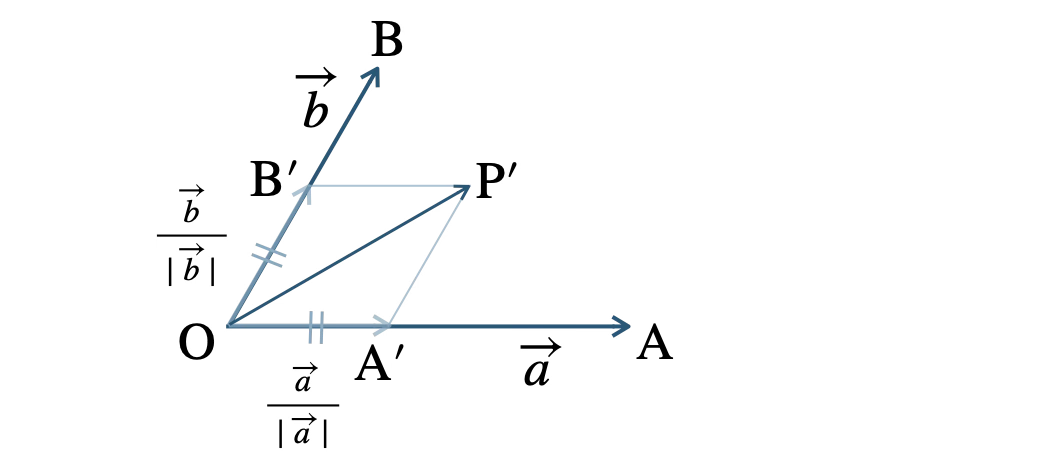

\(\overrightarrow{\rm OA’}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}~,~\overrightarrow{\rm OB’}=\displaystyle\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) となる点 \({\rm A’}~,~{\rm B’}\) をとると、
\(|\,\overrightarrow{\rm OA’}\,|=|\,\overrightarrow{\rm OB’}\,|=1\)
さらに、\(\overrightarrow{\rm OA’}+\overrightarrow{\rm OB’}=\overrightarrow{\rm OP’}\) となる点 \({\rm P’}\) をとると、
\(\overrightarrow{\rm A’P’}=\overrightarrow{\rm OB’}~,~\overrightarrow{\rm B’P’}=\overrightarrow{\rm OA’}\)
となるので、四角形 \({\rm OA’P’B’}\) は平行四辺形である。
また、\(|\,\overrightarrow{\rm OA’}\,|=|\,\overrightarrow{\rm OB’}\,|=1\) より、
\({\rm OA’}={\rm OB’}={\rm A’P’}={\rm B’P’}=1\)
となるので、四角形 \({\rm OA’P’B’}\) はひし形である。
ひし形の対角線は角を二等分するので、\({\rm OP’}\) は \(\angle {\rm A’OB’}\) を二等分する。
ここで、\(\angle {\rm A’OB’}=\angle {\rm AOB}\) であるから、\({\rm OP’}\) は \(\angle {\rm AOB}\) の二等分線上にある。
\(\overrightarrow{\rm OP’}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) の方向が二等分線の方向となるので、
\(\overrightarrow{p}=t\left(\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\right)\) で表される点 \({\rm P}(\overrightarrow{p})\) は \(\angle {\rm AOB}\) の二等分線上にある。[終]
■ この問題の詳しい解説はこちら!
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OC}+\overrightarrow{\rm OD}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{\left(\,\begin{array}{c}5\\[2pt]1\\[2pt]8\end{array}\,\right)+\left(\,\begin{array}{c}3\\[2pt]-3\\[2pt]6\end{array}\,\right)\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\,\begin{array}{c}8\\[2pt]-2\\[2pt]14\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}4\\[2pt]-1\\[2pt]7\end{array}\,\right)\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}&=&\overrightarrow{\rm OM}-\overrightarrow{\rm OB}
\\[5pt]~~~&=&\left(\,\begin{array}{c}4\\[2pt]-1\\[2pt]7\end{array}\,\right)-\left(\,\begin{array}{c}1\\[2pt]3\\[2pt]2\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}4-1\\[2pt]-1-3\\[2pt]7-2\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}3\\[2pt]-4\\[2pt]5\end{array}\,\right)\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm CD}&=&\overrightarrow{\rm OD}-\overrightarrow{\rm OC}
\\[5pt]~~~&=&\left(\,\begin{array}{c}3\\[2pt]-3\\[2pt]6\end{array}\,\right)-\left(\,\begin{array}{c}5\\[2pt]1\\[2pt]8\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}3-5\\[2pt]-3-1\\[2pt]6-8\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}-2\\[2pt]-4\\[2pt]-2\end{array}\,\right)\end{eqnarray}\)
ここで、\(\overrightarrow{\rm BM}\) と \(\overrightarrow{\rm CD}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm CD}&=&3\cdot(-2)+(-4)\cdot(-4)+5\cdot(-2)
\\[3pt]~~~&=&-6+16-10
\\[3pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm BM}\neq\overrightarrow{0}~,~\overrightarrow{\rm CD}\neq\overrightarrow{0}\) より、\( {\rm BM}\perp{\rm CD} \)
\({\small (2)}~\) \( \displaystyle \frac{\,1\,}{\,3\,} \) \({\small (3)}~\) \( 5\sqrt{2} \) \({\small (4)}~\) \( \displaystyle \frac{\,50\,}{\,3\,} \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\)[証明] \({\small (1)}\) より、
\(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm CD}+\overrightarrow{\rm BC}\cdot\overrightarrow{\rm AD}+\overrightarrow{\rm CA}\cdot\overrightarrow{\rm BD}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\(\overrightarrow{\rm AB}\perp\overrightarrow{\rm CD}\) より、\(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm CD}=0~ ~ ~ \cdots {\small [\,2\,]}\)
\(\overrightarrow{\rm BC}\perp\overrightarrow{\rm AD}\) より、\(\overrightarrow{\rm BC}\cdot\overrightarrow{\rm AD}=0~ ~ ~ \cdots {\small [\,3\,]}\)
\({\small [\,1\,]}\)、\({\small [\,2\,]}\)、\({\small [\,3\,]}\) より、
\(\overrightarrow{\rm CA}\cdot\overrightarrow{\rm BD}=0\)
したがって、\( \overrightarrow{\rm CA}\neq 0~,~\overrightarrow{\rm BD}\neq 0~,~\overrightarrow{\rm CA}\cdot\overrightarrow{\rm BD}=0 \) より、\( \overrightarrow{\rm CA}\perp\overrightarrow{\rm BD} \) [終]
■ この問題の詳しい解説はこちら!
\( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \)
とおくと、
点 \( {\rm P} (\, \overrightarrow{p} \,) \) は \( {\rm OA} \) を \( 1:2 \) に内分する点より、
\( \overrightarrow{p}=\displaystyle \frac{\,\overrightarrow{a}\,}{\,3\,} \)
点 \( {\rm R} (\, \overrightarrow{r} \,) \) は \( {\rm CB} \) を \( 1:2 \) に内分する点より、
\( \overrightarrow{r}=\displaystyle \frac{\,2\overrightarrow{c}+\overrightarrow{b}\,}{\,3\,} \)
点 \( {\rm Q} (\, \overrightarrow{q} \,) \) は \( {\rm AB} \) を \( 3:1 \) に内分する点より、
\( \overrightarrow{q}=\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}\,}{\,4\,} \)
点 \( {\rm S} (\, \overrightarrow{s} \,) \) は \( {\rm OC} \) を \( 3:1 \) に内分する点より、
\( \overrightarrow{s}=\displaystyle \frac{\,3\overrightarrow{c}\,}{\,4\,} \)
ここで、線分 \( {\rm PR} \) を \( 3:1 \) に内分する点は、
\(\begin{eqnarray}~~~\displaystyle \frac{\,\overrightarrow{p}+3\overrightarrow{r}\,}{\,4\,}&=&\displaystyle \frac{\,\displaystyle \frac{\,\overrightarrow{a}\,}{\,3\,}+3\cdot\displaystyle \frac{\,2\overrightarrow{c}+\overrightarrow{b}\,}{\,3\,}\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\displaystyle \frac{\,\overrightarrow{a}\,}{\,3\,}+\displaystyle \frac{\,6\overrightarrow{c}+3\overrightarrow{b}\,}{\,3\,}\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}+6\overrightarrow{c}\,}{\,3\,}\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}+6\overrightarrow{c}\,}{\,12\,}\end{eqnarray}\)
また、線分 \( {\rm SQ} \) を \( 1:2 \) に内分する点は、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\overrightarrow{s}+\overrightarrow{q}\,}{\,3\,}&=&\displaystyle \frac{\,2\cdot\displaystyle \frac{\,3\overrightarrow{c}\,}{\,4\,}+\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}\,}{\,4\,}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\displaystyle \frac{\,6\overrightarrow{c}\,}{\,4\,}+\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}\,}{\,4\,}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}+6\overrightarrow{c}\,}{\,4\,}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+3\overrightarrow{b}+6\overrightarrow{c}\,}{\,12\,}\end{eqnarray}\)
したがって、線分 \( {\rm PR} \) を \( 3:1 \) に内分する点と線分 \( {\rm SQ} \) を \( 1:2 \) に内分する点は一致する [終]
■ この問題の詳しい解説はこちら!
解法のPoint|座標平面に接する球面の方程式
\({\small (2)}~\) 中心 \( (-2~,~-1~,~1) \)、半径 \( 3 \)
解法のPoint|球が平面と交わってできる円の方程式
\({\small (3)}~\) \( (2~,~3~,~4)~,~(-2~,~0~,~5) \)
■ この問題の詳しい解説はこちら!
\({\small (2)}~\displaystyle \frac{\,x-3\,}{\,5\,}=y-4=\displaystyle \frac{\,z+2\,}{\,4\,}\)
解法のPoint|座標空間の直線のベクトル方程式
\({\small (3)}~x=5~,~z=3\)
解法のPoint|座標空間の直線のベクトル方程式
\({\small (2)}~x+2=y=-z+2\)
\({\small (3)}~\displaystyle \frac{\,x-3\,}{\,2\,}=-z+4~,~y=-2\)
\({\small (4)}~x=-2~,~z=3\)
解法のPoint|座標空間の直線のベクトル方程式
解法のPoint|座標空間の直線のベクトル方程式
次のページ「2章 平面上の曲線」